




 Stonehenge—An Eclipse Predictor
Stonehenge—An Eclipse Predictor
F. Hoyle
Editor’s Note
During the 1960s there was considerable interest in, and debate about, the purpose of the ancient Stonehenge monument in western England. While British astronomer Fred Hoyle was not the first to suggest that Stonehenge was used to predict eclipses, he does demonstrate here how it could more accurately predict them if the “Aubrey circle” represents the ecliptic (the plane of the Solar System, in which the planets orbit the Sun). 中文
THE suggestion that Stonehenge may have been constructed with a serious astronomical purpose has recently received support from Hawkins, who has shown 1 that many alignments of astronomical significance exist between different positions in the structure. Some workers have questioned whether, in an arrangement possessing so many positions, these alignments can be taken to be statistically significant. I have recently reworked all the alignments found by Hawkins. My opinion is that the arrangement is not random. As Hawkins points out, some positions are especially relevant in relation to the geometrical regularities of Stonehenge, and it is these particular positions which show the main alignments. Furthermore, I find these alignments are just the ones that could have served far-reaching astronomical purposes, as I shall show in this article. Thirdly, on more detailed investigation, the apparently small errors, of the order of ±1°, in the alignments turn out not to be errors at all. 中文
In a second article 2 Hawkins goes on to investigate earlier proposals that Stonehenge may have operated as an eclipse predictor. The period of regression of the lunar nodes, 18.61 years, is of especial importance in the analysis of eclipses. Hawkins notes that a marker stone moved around the circle of fifty-six Aubrey holes at a rate of three holes per year completes a revolution of the circle in 18.67 years. This is close enough to 18.61 years to suggest a connexion between the period of regression of the nodes and the number of Aubrey holes. In this also I agree with Hawkins. I differ from him, however, in the manner in which he supposes the eclipse predictor to have worked. Explicitly, the following objections to his suggestions seem relevant:
(1) The assumption that the Aubrey holes served merely to count cycles of 56 years seems to me to be weak. There is no need to set out fifty-six holes at regular intervals on the circumference of a circle of such a great radius in order to count cycles of fifty-six.
(2) It is difficult to see how it would have been possible to calibrate the counting system proposed by Hawkins. He himself used tables of known eclipses in order to find it. The builders of Stonehenge were not equipped with such post hoc tables.
(3) The predictor gives only a small fraction of all eclipses. It is difficult to see what merit would have accrued to the builders from successful predictions at intervals as far apart as 10 years. What of all the eclipses the system failed to predict 中文
My suggestion is that the Aubrey circle represents the ecliptic. The situation shown in Fig. 1 corresponds to a moment when the Moon is full. The first point of Aries γ has been arbitrarily placed at hole 14. S is the position of the Sun, the angle ⊙ is the solar longitude, M is the projection of the Moon on to the ecliptic, N is the ascending node of the lunar orbit, N ´ the descending node, and the centre C is the position of the observer. As time passes, the points S , M , N and N ´ move in the senses shown in Fig. 1. S makes one circuit a year. M moves more quickly, with one circuit in a lunar month. One rotation of the line of lunar nodes NN ´ is accomplished in 18.61 years. In Fig. 1, S and M are at the opposite ends of a diameter because the diagram represents the state of affairs at full Moon. 中文
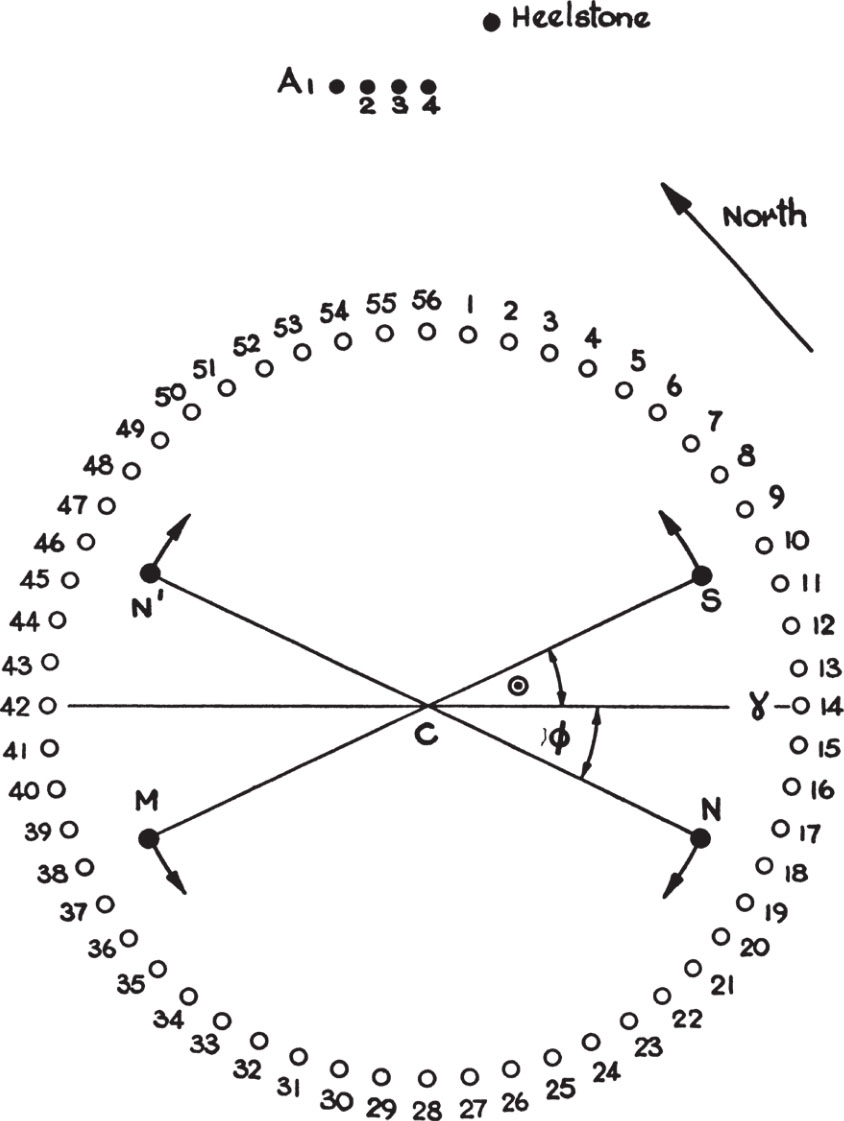
Fig. 1
If the Moon is at N , there is a solar eclipse if the Sun is within roughly ±15° of N , and a lunar eclipse if the Sun is within ±10° of N ´. Similarly, if the Moon is at N ´, there will be a solar eclipse if the Sun is within ±15° of coincidence with the Moon, and a lunar eclipse if it is within roughly ±10° of the opposite end of the line of lunar nodes. Evidently if we represent S , M , N and N ´ by markers, and if we know how to move the markers so as to represent the actual motions of the Sun and Moon with adequate accuracy, we can predict almost every eclipse, although roughly half of them will not be visible from the position of the observer. This is a great improvement on the widely scattered eclipses predictable by Hawkins’s system. Eclipses can occur as many as seven times in a single year, although this would be an exceptional year. 中文
The prescriptions for moving the markers are as follows: (1) Move S anticlockwise two holes every 13 days. (2) Move M anticlockwise two holes each day. (3) Move N and N ´ clockwise three holes each year. 中文
We can reasonably assume that the builders of Stonehenge knew the approximate number of days in the year, the number of days in the month, and the period of regression of the nodes. The latter follows by observing the azimuth at which the Moon rises above the horizon. If in each lunar month we measure the least value of the azimuth (taken east of north), we find that the “least monthly values” change slowly, because the angle φ = NC γ changes. The behaviour of the “least monthly values” is shown in Fig. 2 for the range –60°≤φ≤60°. (The azimuthal values in Fig. 2 were worked out without including a refraction or a parallax correction. These small effects are irrelevant to the present discussion.) The least monthly values oscillate with the period of φ, 18.61 years. By observing the azimuthal cycle, the period of φ can be determined with high accuracy by observing many cycles. At Stonehenge sighting alignments exist that would have suited such observations. With the periods of S , M and N known with reasonable accuracy the prescriptions follow immediately as approximate working rules. 中文
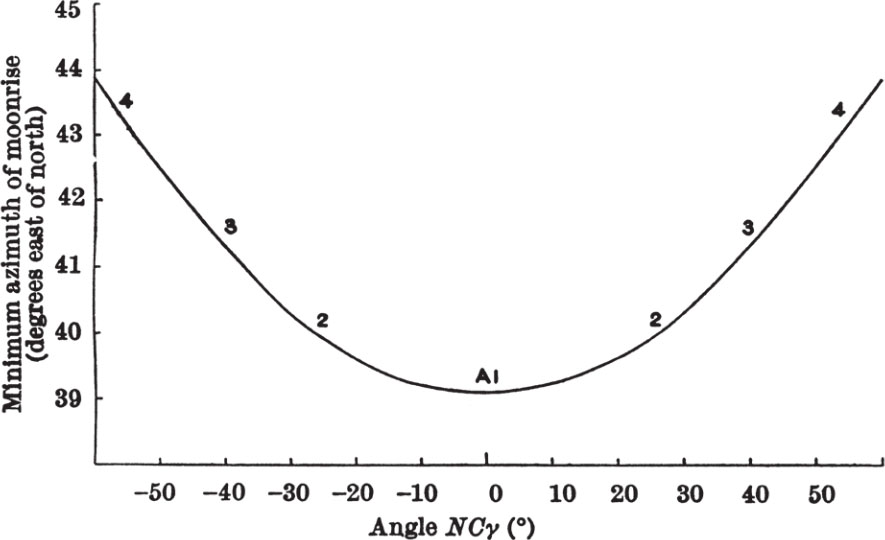
Fig. 2
Suppose an initially correct configuration for M , N and S is known. The prescriptions enable us to predict ahead what the positions of M , N and S are going to be, and thus to foresee coming events—but only for a while, because inaccuracies in our prescriptions will cause the markers to differ more and more from the true positions of the real Moon, Sun, and ascending node. The lunar marker will be the first to deviate seriously—the prescription gives an orbital period of 28 days instead of 27.32 days. But we can make a correcting adjustment to the M marker twice every month, simply by aligning M opposite S at the time of full Moon, and by placing it coincident with S at new Moon. The prescription for S gives an orbital period of 364 days, which is near enough to the actual period because it is possible to correct the position of S four times every year, by suitable observations made with the midsummer, midwinter, and equinoctial sighting lines that are set up with such remarkable accuracy at Stonehenge. 中文
Stonehenge is also constructed to determine the moment when φ=0, that is, when N should be set at γ. The line C to A l of Fig. 1 is the azimuthal direction for the minimum point of Fig. 2. By placing N at γ when the Moon rises farthest to the north, the N marker can be calibrated once every 18.61 years. The prescription implies only a small error over one revolution of N . If N started correctly, it would be out of its true position by only 1° or so at the end of the first cycle. The tolerance for eclipse prediction is about 5°, so that if we were to adjust N every cycle, the predictor would continue to work indefinitely without appreciable inaccuracy. The same method also serves to place N at the beginning. 中文
But now we encounter an apparent difficulty. The minimum of Fig. 2 is very shallow and cannot really be determined in the way I have just described. Angular errors cannot have been less than ±0.25°, and even this error, occurring at the minimum of Fig. 2, is sufficient to produce an error of as much as ±15° in φ. 中文
The correct procedure is to determine the moment of the minimum by averaging the two sides of the symmetrical curve, by taking a mean between points 2, for example. The inaccuracy is then reduced to not more than a degree or two—well within the permitted tolerance. 中文
What is needed is to set up sighting directions a little to the east of the most northerly direction. The plan of Stonehenge shows a line of post holes, A l, 2, 3 and 4, placed regularly and with apparent purpose in exactly the appropriate places. 中文
The same point applies to solsticial measurements of the Sun. In summer the sighting line should be slightly increased in azimuth, in winter it should be slightly decreased. 中文
Hawkins 1 gives two tables in which he includes columns headed “Error Alt.”. These altitude errors were calculated on the assumption that the builders of Stonehenge intended to sight exactly the azimuthal extremes. The test of the present ideas is whether the calculated “errors” have the appropriate sign—on the argument given here “errors” should be present and they should have the same sign as the declination. In ten out of twelve values which Hawkins gives in his Table 1 this is so. The direction from C to the Heelstone is one of the two outstanding cases. Here the “error” is zero, suggesting that this special direction was kept exactly at the direction of midsummer sunrise, perhaps for aesthetic or ritualistic reasons. The other discrepant case is 91→94. Here my own calculation gives only a very small discrepancy, suggesting that this direction was also kept at the appropriate azimuthal extreme. 中文
Negative values of the altitude error correspond to cases where it would be necessary to observe below the horizontal plane, if the objects in question were sighted at their extreme azimuths. This is impossible at Stonehenge because the land slopes gently upward in all directions. Such sighting lines could not have been used at the extremes, a circumstance which also supports this point of view. 中文
It is of interest to look for other ways of calibrating the N marker. A method, which at first sight looks promising, can be found using a special situation in which full Moon happens to occur exactly at an equinox. There is evidence that this method was tried at Stonehenge, but the necessary sighting lines are clearly peripheral to the main structure. Further investigation shows the method to be unworkable, however, because unavoidable errors in judging the exact moment of full Moon produce large errors in the positioning of N . The method is essentially unworkable because the inclination of the lunar orbit is small. Even so, the method may well have caused a furore in its day, as the emphasis it gives to a full Moon at the equinox could have been responsible for the dating of Easter. 中文
An eclipse calibrator can be worked accurately almost by complete numerology, if the observer is aware of a curious near-commensurability. Because S and N move in opposite directions the Sun moves through N more frequently than once a year, in 346.6 days. Nineteen such revolutions is equal to 6,585.8 days, whereas 223 lunations is equal to 6,585.3 days. Thus after 223 lunations the N marker must bear almost exactly the same relation to S that it did before. If the correct relation of N to S is known at any one moment N can be reset every 223 lunations; that is, every 18 years 11 days. The near-commensurability is so good that this system would give satisfactory predictions for more than 500 years. It requires, of course, S to be set in the same way as before. The advantage is that in the case of N it obviates any need for the observational work described above. But without observations the correct initial situation cannot be determined unless the problem is inverted. By using observed eclipses the calibrator could be set up by trial and error. This is probably the method of the Saros used in the Near East. There is no evidence that it was used at Stonehenge. The whole structure of Stonehenge seems to have been dedicated to meticulous observation. The method of Stonehenge would have worked equally well even if the Saros had not existed. 中文
Several interesting cultural points present themselves. Suppose this system was invented by a society with cultural beliefs associated with the Sun and Moon. If the Sun and Moon are given godlike qualities, what shall we say of N ? Observation shows that whenever M and S are closely associated with N , eclipses occur. Our gods are temporarily eliminated. Evidently, then, N must be a still more powerful god. But N is unseen. Could this be the origin of the concept of an invisible, all-powerful god, the God of Isaiah? Could it have been the discovery of the significance of N that destroyed sun-worship as a religion? Could M , N and S be the origin of the doctrine of the Trinity, the “three-in-one, the one-in-three”? It would indeed be ironic if it turned out that the roots of much of our present-day culture were determined by the lunar node. 中文
( 211 , 454-456; 1966)
Fred Hoyle: University of Cambridge.
References: