




 Evidence in Support of a Rotational Model for the Pulsar
PSR
0833–45
Evidence in Support of a Rotational Model for the Pulsar
PSR
0833–45
V. Radhakrishnan et al.
Editor’s Note
This paper, appearing within a few months of the discovery of pulsating stars (pulsars), is an almost immediate confirmation of Gold’s theory that the apparent pulsation is caused by rapid rotation, sending a beam of radiation across the sky much as a lighthouse announces its presence. Radhakrishnan was trained as a radioastronomer in India and Australia; he was a son of the Nobel-Prize-winning scientist C. V. Raman and succeeded him as Director of the physical laboratory in Bangalore. 中文
THE pulsar PSR 0833–45, discovered at the Molonglo Radio Observatory 1 and tentatively identified with the supernova remnant Vela X , has been observed with the Parkes 210 foot reflector at frequencies of 2,700 MHz and 1,720 MHz. We find that this pulsar is remarkable for its short pulse width, high and constant intensity, complete linear polarization and changing periodicity. Our observations of this object seem to rule out radial pulsations as the source of the radio emission and support a rotational hypothesis along the lines suggested by Gold 2 and discussed by Goldreich 3 as the most likely model. 中文
The first observations were made on December 8, 9 and 10 using the wideband correlation receiver 4 operating at 2,700 MHz. The pulse energy, linear polarization and an accurate period were measured and are listed in Table 1. Attempts to obtain a pulse shape, however, soon indicated that the drift time of ~ 10 ms through the 500 MHz effective passband of the receiver was smoothing out the natural pulse beyond recognition. It seemed probable that the polarization characteristics of the pulse were also being smeared by the passband. Observations of the pulsar were therefore repeated on the nights of December 11, 12, 13 and 20 at 1,720 MHz with narrower bandwidths. The fast rise and short duration of the pulse as recorded by a 400 channel integrator 5 are illustrated in Fig. 1. Apart from occasional pulses of extraordinary strength, the amplitude variations were so low that an average of 100 pulses taken at any time during the several days this pulsar was observed on either frequency showed less than 10 percent variation in amplitude and even less in pulse shape. Large et al. 6 have remarked on similar behaviour at 408 MHz. Table 1 lists various parameters obtained from measurements at either one or both of the observing frequencies. 中文
Table 1. Characteristics of PSR 0833–45
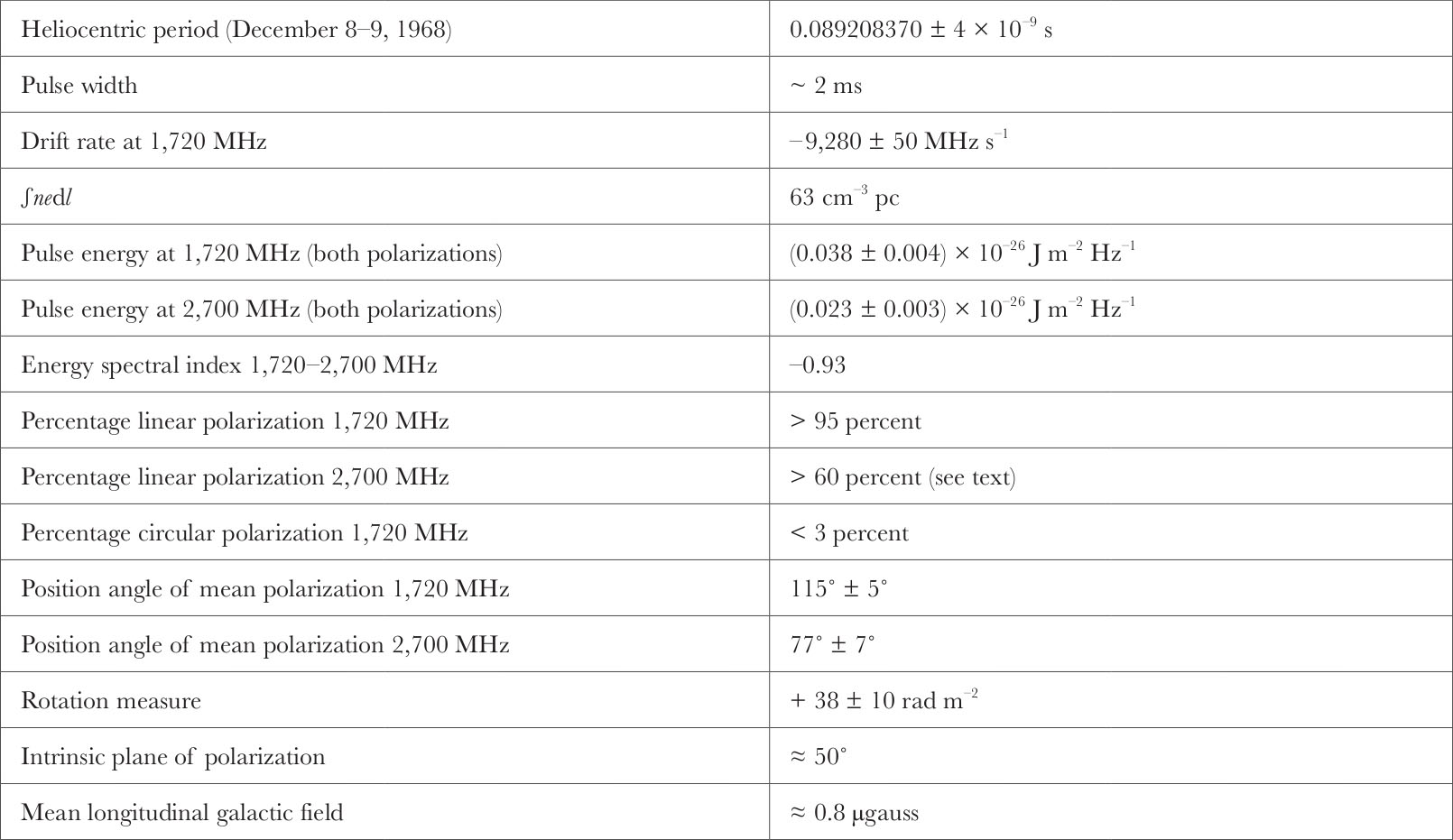
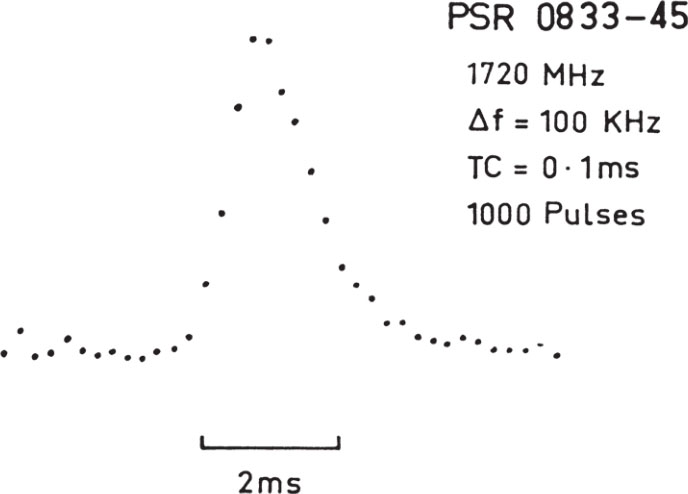
Fig. 1. A 1,000 pulse integration at 1,720 MHz of PSR 0833–45. The channel separation is approximately 0.22 ms.
The drift rate of the pulse at 1,720 MHz was measured by timing the arrival of the pulses in 100 kHz filters separated by 6 MHz. The interstellar dispersion derived from this measurement is somewhat higher than the value quoted by Large et al. 6 but not significantly so. The pulse energy at 1,720 MHz was obtained by integrating the observed pulses in two opposite polarizations. This is plotted in Fig. 2 together with the 2,700 MHz value and the 408 MHz energy 6 . The spectrum shows no break at the higher frequencies and in this respect PSR 0833–45 resembles CP 1133 (ref. 7). 中文
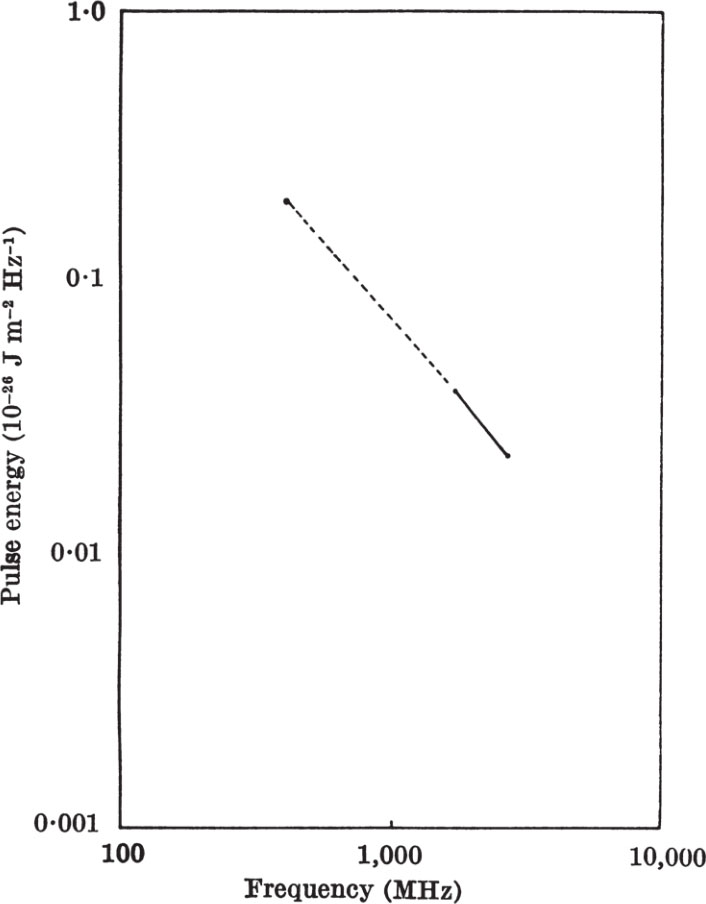
Fig. 2. The high frequency energy spectrum of PSR 0833–45. The spectral index is essentially constant at –0.9 between 408 MHz and 2,700 MHz.
The position angle at 1,720 MHz of the mean plane of linear polarization over the pulse was measured on the four nights of observation at this frequency and found to be the same. The internal agreement was considerably better than the error of 5 percent quoted in Table 1 for the absolute value of the position angle. The measurements of the position angle at 2,700 MHz on the previous three nights were also found to have remarkable internal consistency. Combining these two measurements on the assumption that the plane of polarization at these frequencies is indeed constant in time, and the same at the source, we have obtained a rotation of 38° ± n 180° between these two frequencies. For n = 0 the corresponding rotation measure is +38 ± 10 rad m –2 . The mean value for the rotation measure in the region of Vela X obtained by Milne 8 is +46 rad m –2 . In view of the variations of rotation measure within the region the agreement is reasonable and provides strong support for the identification 1 of this pulsar with the supernova remnant. The average longitudinal component of the galactic magnetic field in this direction was then derived from the dispersion and the rotation measure 9 . A value of 0.8 μgauss was obtained which is intermediate between the values obtained by Smith 9,10 for three other pulsars in different directions in the galaxy. 中文
The distribution of polarization across the pulse at 1,720 MHz is illustrated in Fig. 3. The Stokes parameter V has not been shown, for the circular polarization was found to be less than 3 percent. The whole pulse is almost completely linearly polarized (>95 percent) with the direction of the plane of polarization varying systematically across the main peak of the pulse. The Q axis was chosen as 115° to coincide with the polarization of the peak of the pulse. The plane of polarization rotates uniformly from a polarization angle (PA) near 140° on one edge of the pulse to less than PA 90° on the other, as sketched in Fig. 4. The magnetic field lines responsible for the polarization must vary smoothly over a similar range, for the amplitude of the radiation builds up from zero to a maximum and then falls off again. Detailed measurements across the pulse were not possible with the 2,700 MHz receiver because of the wide bandwidth as mentioned earlier. There were clear indications that the plane of polarization did change by about 40°–60° across the pulse, however. The smoothed pulse shapes obtained on different polarizations were consistent with the assumption that the polarization structure of the pulse was similar to that found at 1,720 MHz. 中文
Fig. 3. The distribution of linear polarization across the pulse at 1,720 MHz. The distribution of Q and – U represents a gradual change of approximately 45° in the position angle of polarization across the pulse. Within the errors of measurement the pulse is completely polarized.
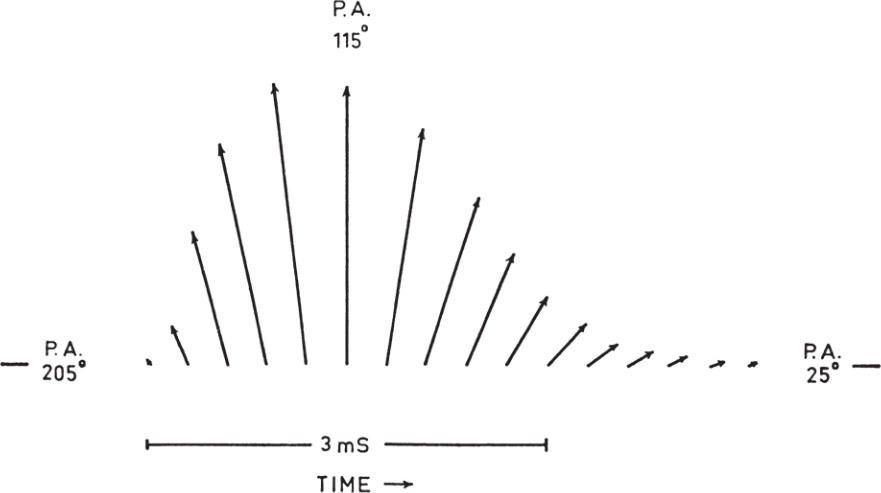
Fig. 4. Sketch showing the rocking of the plane of polarization during the pulse from PSR 0833–45.
Mills 11 reports that the pulsar in the Crab nebula has been observed at Arecibo and found to be slowing down in periodicity by one part in 2,400 yr –1 . He further suggested that as PSR 0833–45 has the next shortest period known, it might also exhibit the same characteristic. Following up his suggestion we made several other measurements of the period and the results are illustrated in Fig. 5. 中文
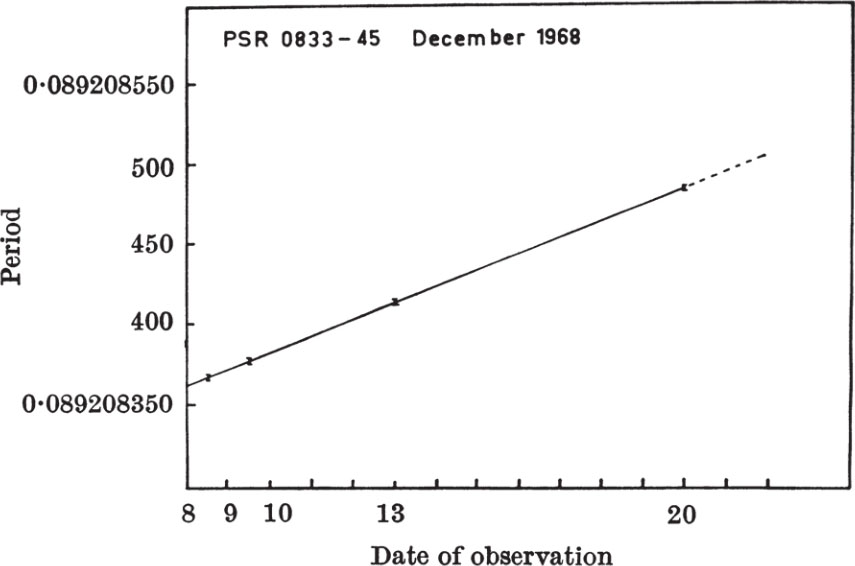
Fig. 5. The variation of the period of PSR 0833–45 over the 12 day observing span. The slope corresponds to an increase in the period of 10 ns or 1 part in 10 7 day –1 .
The period of PSR 0833–45 is increasing at the rate of 10 ns day –1 , or one part in 24,000 yr –1 . Assuming the position for the pulsar given by Large et al. 6 we have used all our measurements to give the heliocentric period P =0 s · 089208483 ± 2 × 10 –9 + R (Julian date = 2440210.0) where the rate of increase R = (10 ± 0.4) × 10 –9 s. In the notation of Moffet and Ekers 7 the stability Δ P/P ≈ 1.2 × 10 –13 . 中文
It seems reasonable to assume that the polarization of the radiation from pulsars reflects the magnetic field in the region of generation. A very highly linearly polarized pulse must then imply that all of the radiation in the pulse was generated in, or modified in, passage through a small region where the field was essentially homogeneous. If successive pulses all have exactly the same polarization, then it must mean that the same locality in the magneto-sphere of the pulsar remains in view for as long as the polarization remains constant. We have observed PSR 0833–45 on December 11, 12, 13 and 20 at 1,720 MHz for many hours each night and never detected any measurable change in either the degree or plane of polarization. It must follow that either a pulsating source of radiation or a “window” through which we periodically glimpse a steady source of radiation is permanently linked to one region in the magnetic field of the star. All of the observed characteristics of the pulse can be reasonably understood by assuming a rotating neutron star model as suggested by Gold 2 . Any hypothesis associating the radio pulses with radial oscillations of the star must invoke one of three special conditions: ( a ) the magnetic field is stationary as viewed from our frame of reference, ( b ) the rotation of the pulsar is synchronous with its pulsation, or ( c ) the rotational and magnetic axes of the star are aligned. ( a ) is extremely unlikely, ( b ) is unlikely in general and particularly so on the basis of our observations which show a slowing down of the pulse rate but no change in the polarization, and ( c ) can be dismissed from symmetry considerations in view of the observed systematic sweeping of the plane of polarization across the pulse. 中文
That the two most rapidly pulsating sources have shown an increase in period with time as predicted on Gold’s model adds further support to the rotation hypothesis. Goldreich 3 has developed a simple axisymmetric version and shown that relativistic particles must be carried out along the field lines which extend beyond the velocity of light cylinder. If a pulsar is a non-axisymmetric version of this model as suggested, the beaming of the radiation in any given direction will be governed by the geometry linking the line of sight with the magnetic and rotational axes of the star. If this were indeed the case the average pulse shape would represent the profile of the magnetic “window” through which radiation can escape in a given direction, and the polarization of the pulse would be independent of frequency. Such a model would justify the tacit assumption in Faraday rotation interpretations that different frequencies are generated with the same polarization at the source. Any change of polarization across the pulse would then correspond to the rotation of the field lines in the duration of the pulse. A change of more the 45° in the plane of polarization such as seen in PSR 0833–45 implies that the radiation must emanate from a region close to the magnetic pole with the magnetic axis inclined at a considerable angle to the rotational axis. 中文
We consider it relevant to draw attention to certain similarities between Jupiter and the pulsars. The low frequency radiation from both is characterized chiefly by unpredictability and fantastic complexity in structure and polarization. At the higher frequencies the polarization of Jupiter’s radiation is chiefly linear, periodic and highly predictable. Over 180° of rotation the total intensity rises and falls due to beaming while the plane of polarization rocks 12 with the magnetic field. It is conceivable that at a high enough frequency the pulses from any pulsar will be as repetitive in character as they are in time. 中文
If pulsars have satellites, and the satellites influence the activity of the pulsar in the manner of Io’s influence on Jupiter 13 , the radiation would exhibit many of the characteristics that are found at low frequencies. In spite of Jupiter’s proximity and the time over which the low frequency radiation had been studied, it was only a statistical approach combined with a knowledge of Io’s movements which finally led to the discovery of the modulation. 中文
Goldreich 3 predicts a rate of change of period inversely proportional to the square of the period. The ratio of the rates of change of the Crab pulsar to the Vela pulsar is 10, in reasonable agreement with the predicted value of 7.5. The age of the Vela supernova on his model would then be ~ 10 4 yr. 中文
We thank Dr. R. N. Manchester for help with the 1,720 MHz observations and Miss P. Beswick for help in the preparation of the manuscript. 中文
( 221 , 443-446; 1969)
V. Radhakrishnan, D. J. Cooke, M. M. Komesaroff and D. Morris: Radiophysics Laboratory, CSIRO, Sydney, Australia.
Received December 30, 1968.
References: