




本章中我们着重介绍图论相关的一些模型和算法。先从一个经典的图论模型——哥尼斯堡七桥问题谈起。
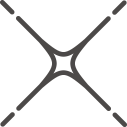
18世纪初在普鲁士的哥尼斯堡城有一条河穿过城市的中心,河中分布着两个小岛,这两个岛与河岸由七座桥连接起来,如图1.1(a)所示。有人提出一个有趣的问题,即一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点。这一问题被命名为哥尼斯堡七桥问题,也被认为是图论学科的起源。这个问题看似非常简单,但是却难住了当时博学的教授们,最后大数学家欧拉解决了这一问题。他解决这一问题的过程可以看作是一个简单的数学建模过程。
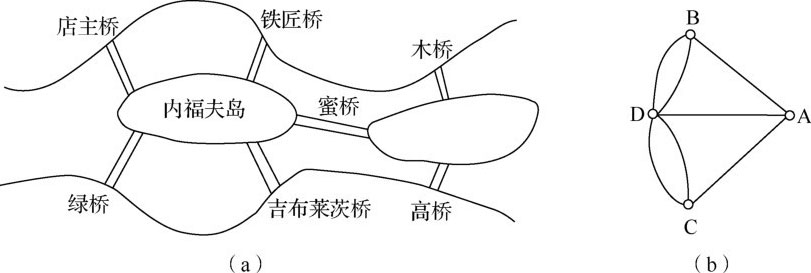
图1.1 哥尼斯堡七桥示意图
第一步,我们把这个问题的本质提炼出来,即人们分别在岸上和岛上行走的路线与距离,桥的形状长度与本问题无关,我们只需要关注过桥的顺序。基于这一考虑,第二步我们可以分别用四个点来表示河的两岸和河中的岛屿,而用点之间的连线表示连接它们之间的桥,这样我们就得到了一张简单的图,如图1.1(b)所示。我们所要求解的问题就转化成了是否可以从图中一点出发,经过每条连线恰好一次回到起点。第三步,我们观察到在经过图中点时必然由一条连线进另一条连线出,因此我们所要求的走法存在的必要条件是图中每个点相关联的连线数目是偶数,从而得出结论,哥尼斯堡七桥问题中所要求的走法是不存在的。
下面我们再给出一个看似和图无关,但可由图来巧妙解决的问题——过河问题。
一只狼,一只羊,一筐菜位于河的同侧。一个摆渡人要将它们运过河去,由于船小,运力有限,一次只能载三者之一。很显然,狼和羊,羊和菜都不能在无人监视的情况下留在一起,那么摆渡人应该怎样把它们运过河呢?
我们的目标是将羊,狼,菜从河的一边运到另一边,在每次摆渡发生后,羊、狼、菜中最多一个以及人的位置会发生变化(即从河岸的一边到另一边),而根据题意,其中一些位置的组合是不可以出现的。因此,整个摆渡过程可以看成是狼、羊、菜、人的位置的可行的变化过程。我们可以建立一张图来刻画这一过程。不妨设开始三者都在河的北岸,需要运到南岸。
我们用一个长度为4的0,1序列来表示人、羊、狼、菜在摆渡发生前或后的位置,其中1表示北岸,0表示南岸。根据要求,我们列出可能的10种状态,分别用平面上10个点来表示,对于它们当中任何两个点,用一条线相连,当且仅当这两点所表示的位置状态可以通过一次摆渡转化。这样我们就得到了一张图(见图1.2),而图中从点(1,1,1,1)经过一些边到点(0,0,0,0)的每一种走法都对应一种可行的摆渡方案。
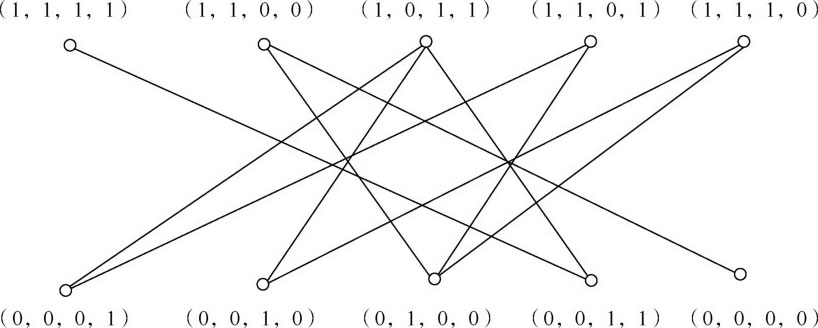
图1.2 人、羊、狼摆渡示意图
如果我们需要找一个最好的方案,很自然就是要找经过边最少(摆渡次数最少)的方案。这点可以通过图论中的最短路径算法实现,我们会在后面的章节中介绍这一算法。
不论是哥尼斯堡七桥问题还是过河问题,我们所建立的模型都是一张简单的“图”,而它就是图论这一学科主要的研究对象。就是这样一个简单的模型与现实生活有着紧密的联系,有着广泛的应用。如图1.3所示是本章所要介绍的模型的关系结构。
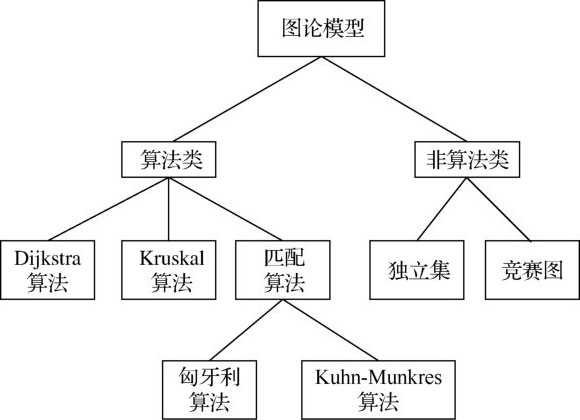
图1.3 图论模型的关系结构

第1章微课