




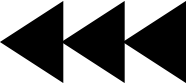
正如人们难以评价来自备择假设的证据的情况一样,人们也很难意识到能够证伪他们焦点假设的证据和检验。与之相反,人们(包括科学家)倾向于寻找能够支持自身理论的证据,而非去证伪理论。推理领域研究中40多年来一个研究最多的问题就充分说明了这点。这项实验任务由彼得·沃森(Peter Wason,1966,1968)创造出来,在之后的多个研究中被检验了数十次(Evans,1972,1996,2007;Evans,Newstead&Byrne,1993;Johnson-Laird,1999,2006;Klauer,Stahl&Erdfelder,2007;Oaksford&Chater,1994,2007;Stenning&van Lambalgen,2004)。请在继续阅读前尝试回答以下这个问题:
下图中的每个方框表示一张桌上的卡片,每张卡片一面是字母,另一面是数字。有一条规律:如果一张卡片字母面是元音的话,那么它的数字面就是偶数。这四张卡片两张是字母面向上,两张是数字面向上。你的任务是为确定这条规律是否正确,决定应该翻转哪(几)张卡片。

这个任务被称作四卡片选取任务,其被大量研究的原因是:大多数人都在这个问题上犯了错,而弄清其中的原因又异常艰难。这个问题的答案看起来很容易。假设的规律说:如果一张卡片字母面是元音,那么它的数字面就是偶数。所以,答案看起来是选择A和8:A是元音,可以看下背面是否是偶数;8是偶数,可以看下背面是否是元音。问题是这个答案——大约有50%的被试都给出了这样的答案——是错误的!第二种普遍的答案——只翻开写有A的卡片(去看背面是否是偶数)——也是错误的!另外还有20%的被试选择了翻转其他的组合(如K和8),仍然是不对的。
如果你与过去数十年来几十个研究中参与这项任务的90%被试一样,那么你也会给出错误的答案。让我们来仔细看一下这么多人是如何犯错的。首先,他们在写有K和A的卡片上都没有犯错。大多数人都没有选择卡片K而选择了卡片A,因为规律对写有辅音的卡片背面是什么并没有规定,因此K与这条规律是无关的。而A不是,它的背面可能是偶数或奇数。前者与规律一致,后者是能够证明这条规律是否正确的关键性结果。简而言之,要证明这条规律不是错误的,必须把卡片A翻过来,这一点是大多数人都意识到了的。
然而,8和5是真正困难的卡片,许多人在这两张卡片上犯了错。他们错误地认为卡片8必须被翻过来,这张卡片被错误地选择是因为,人们认为需要检查下它的背面是元音而不是非元音。但是,比如说,如果8的背面是K的话,并不能证明这条规律就是错的,因为虽然规律说了元音的背面一定是偶数,并没有说偶数的背面一定是元音。所以在偶数的背后发现一个非元音,完全不能说明这条规律到底是对是错。相比之下,5这张卡片大部分人都没有选择,却是真正必须翻的。卡片5的背面可能是一个元音,而如果是这样的话,规律就是错误的了,因为所有的元音背面都不应是一个奇数。因而,要想证明规律不是错的,卡片5必须被翻过来。
总结一下,这条规律的形式是“如果P,那么Q”这种条件情形,要证明它是错的,必须出现一个P的情况下不是Q的例子。因此,P–非Q卡片(我们的例子中的A和5)才是为确定规律的正确性,确定要翻转的两张卡片。如果出现了P–非Q的组合,规律就是错误的。如果没有出现,规律就是对的。
既然这个问题在经过解释后变得非常容易,为什么大多数人都回答错了呢?关于这点有许多理论(参见Cosmides,1989;Evans,2007;Johnson-Laird,1999,2006;Klauer et al.,2007;Margolis,1987;Oaksford&Chater,1994,2007;Sperber,Cara&Girotto,1995),其中提出时间最久的理论之一,至少解释了人们这种不佳表现的部分原因。这种理论持有的观点是,人们只关注了“证实”这条规律,这就是激发他们决定翻开卡片8(想要在背面看到一个元音从而验证假设)和卡片A(想要确认背面是偶数)的原因。他们没有考虑到的是,看一下可能推翻这条规律的证据,而持有这种想法一定会意识到卡片5的关联性(可能在它的背面有一个能推翻假设的元音存在)。如前所述,还有许多其他理论解释人们在这一任务上的不佳表现,但是不论这些描述性理论怎样解释这种错误的产生,关于证伪性的考虑,毫无疑问能够纠正这种错误。
尽管证伪原则在一般性推理中非常有用,有大量的证据表明,这并不是一种自然性策略。还有另外一个实验范式也说明了人们在证伪方面存在问题,即所谓的“2-4-6任务”,也是彼得·沃森(1960)设计的另一个著名推理问题。和四卡片选取任务一样,也有许多其他的理论解释人们在2-4-6任务中表现欠佳的原因(Evans,1989,2007;Evans&Over,1996;Gale&Ball,2006;Klayman&Ha,1987;Poletiek,2001)。但也同四卡片选取任务一样,不论这些描述性理论中的哪个解释了人们在这项任务上的不佳表现,对证伪性的考虑很明显可以改善这种表现。
被试被告知,实验的主试者想了一种对三个整数的集合(三元组)进行分类的规则,三元组2-4-6就符合这个规则。接下来,被试需要自己提出三元组,由主试者回答他们提出的三元组是否符合该规则。被试可以一直提出三元组并获得主试者的反馈,直到他们认为自己已经猜出主试者的这种规则,这时即可宣布自己猜到的规则。
主试者在2-4-6任务中的规则其实是“任何三个依次递增的数字组合”。参与这个任务的被试大多都很难发现这个规则,因为他们一开始就对规则抱有一种过于狭窄的假设。他们猜测的规则,诸如“递增的偶数”或“以相同间隔增加的数字”,进而产生的三元组都是与这些过于限定性的规则相一致的。被试因而获得了很多他们产生的三元组是正确的反馈,而当他们说出自己的假设时,对假设是错误的答复感到非常惊讶。例如,被试产生的一种典型的三元组序列(见Evans,1989)是8-10-12、14-16-18和40-42-44。获得三个肯定后,他们宣布,规则就是“每次增加2的数字组合”。当被告知这并不正确时,他们可能进而产生一些序列,如2-6-10、0-3-6和1-50-99,又获得了肯定性反馈。这时他们又会宣布一个类似“规则是相邻数之间的间隔是相等的”这种规则,而这同样也是错误的。他们没能做到的是,提出一些与他们的假设严重不符的、可能证伪他们假设的序列,比如100-90-80或1-15-2。
被试并没有认真地尝试去推翻他们的焦点假设,一种能够极大改善人们在此类任务上表现的实验操作也说明了这点。特韦尼、多尔蒂、华纳和普利斯科(Tweney,Doherty,Warner&Pliske,1980)进行了一项实验,被试被告知主试者想了两种规则:一种规则适用于名为DAX的三元组;另一个适用于名为MED的三元组。每一次由被试说出一个三元组,主试者告诉他这个三元组是DAX还是MED。首先告诉被试2-4-6是DAX,之后的实验进行方式如前所述。DAX同之前一样被定义为“任何三个递增数的集合”,MED则被定义为“任何其他的情况”。在这种情况下,由于被试需要经常在对DAX和MED的正性检验中来回调整,反而能够更轻易地解决问题。当然,现在的情况是,对MED的正性检验即对DAX的证伪。因为有另一种要求关注MED的正性、突出、生动化的假设存在,被试被驱使着对DAX进行了证伪操作。实验所设置的另一个类别穷尽了所有可能的假设,并且和原有的焦点假设间是互相排斥的,因而每次被试在试图确认一种假设时,相当于同时也在证伪另一种假设。通过这种方式,被试被驱使做了一些他们通常不会做的事——关注备择假设以及证伪焦点假设。显然,人们需要通过一种人为的方式才能被诱导去这样做,这也再一次印证了要让人们去注意焦点假设可能是错误的是件多么困难的事。
综上所述,坏消息是,人们很难想到能够证伪他们的焦点假设的证据;好消息则是,这种思维能力是可以学习的。所有的科学家都要经过这样一个训练过程,包括很多尝试证伪他们持有的焦点假设的练习,以及经常对自己进行口头的质询,“我还应考虑什么其他假设”?