




要想做到认识性理性,个体必须校正自身对概率的信念,使其与实际证据所示的概率相一致。这种概率推理的一个规范模型就是所谓的“概率演算”。从数学上来看,概率值遵循着特定的规则,这些规则构成了主观概率估测中最重要的一种规范模型。因此,要想具备认识性理性,在估计概率时就必须要符合概率的客观规则。这些规则中的大部分都是很直观的,以下是其中最重要的几个:
概率值在0~1变化,因此0≤P(A)≤1,这里P(A)是事件A发生的概率。
如果一个事件肯定会发生,那么它的概率值就是1.0。因此,当A是确定事件时,P(A)=1。
如果一个事件肯定不会发生,那么它的概率值就是0。因此,当A是不可能事件时,P(A)=0。
如果事件A和B不能同时发生,它们被称作是互斥的。如果事件A和B是互斥的,那么其中任意一个事件发生的概率就是对每个事件发生的概率值进行加总
P(A或B)=P(A)+P(B)
条件概率涉及在另一个事件发生的情况下,某个事件发生的概率。它的表示方法是:P(A/B),对其的描述方法有多种,包括“给定B后A的概率”“B发生的条件下A的概率”,以及“假定B发生后A发生的概率”。
如果A和B是互斥的,那么P(A/B)=0,因为如果B发生了,A就不能发生。然而,当A和B不是互斥关系时,条件概率的公式即下所示
P(A/B)=P(A和B)/P(B)
要注意到,一般来说,P(A/B)和P(B/A)的值是不一定相同的,因为后者的公式中含有一个不同的分母
P(B/A)=P(A和B)/P(A)
不过,我们可以用一个条件概率来表示另一个。事实上,在经过一些简单的数学运算后,我们就可以得到决策理论中最著名的理论之一——贝叶斯定理,有时也称“贝叶斯规则”。但在这么做之前,需要先说明后面会出现的一些数学符号。首先,稍后内容是本书中涉及数学及专业运算最多的部分。但是,在这里最重要的并非是数学能力,而是这种概念。即使你对数学有恐惧心理,想把这些数字和公式都忽略掉,也应当在整个讨论中明确认识到这种数学概念的重要性。这一点很关键,因为要成为一名贝叶斯式思考者,你需要学习的正是这种思维方式(一些口头规则)。正式的贝叶斯统计当然需要运算,但要想摆脱与概率相关的思维错误,我们只需学习一些关于概率正确思维的概念逻辑。
强调过这些需要注意的问题后,以下即为贝叶斯规则
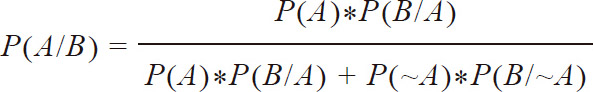
这个规则里只有一项我们没有见过,~A,指的是“非A”。因此,P(~A)指的是非A的事件发生的概率大小。
决策科学家的研究表明,如果我们的概率判断不遵从刚才提到的这些关于概率的简单规则的话,就会产生一些对自身不利的结果(同第2章讨论过的金钱泵效应类似)。例如,如果你觉得新英格兰爱国者队赢得下一届美国橄榄球超级杯的概率是0.25,芝加哥小熊队获胜的概率是0.10,那么你应当认为爱国者队或者小熊队获胜的概率是0.35(回忆之前出现过的公式P(A或B)=P(A)+P(B))。一旦你违背了这个规则,就不是认识性理性的,你基于这些概率估计所做的任何行动也都不是最优的,这些行动不会最大化你的期望效用。
所有的概率规则都很重要,但对于判断和决策问题,贝叶斯定理有着更加突出的重要性。自从18世纪出生在英格兰坦布里奇韦尔斯的牧师托马斯·贝叶斯发现贝叶斯公式后(Stigler,1983,1986),其使用范围已远远超出了仅将一种条件概率P(B/A)转换成另一种条件概率P(A/B)的简单用途。在人们进行信念更新这一重要任务中,它作为一个正式标准被广泛使用。这一公式的用途是,计算对于某个特定假设的信念在接收到有关这个假设的新证据后,该如何对信念进行更新的问题。我们所要做的,只是将原来公式中的A和B换成两个基本的概念:被审查的焦点假设(focal hypothesis,标为H),以及收集到的有关假设的一套数据(标为D)。
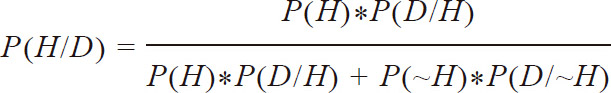
在这个公式中你会看到另外一个符号,~H(非H),指的就是备择假设:在焦点假设H错误时,必然正确的互斥假设。因此,按照规则,备择假设(~H)正确的概率,就是1减去焦点假设H正确的概率。例如,如果我认为我钓上来的鱼是一条鲑鱼的概率是0.60,那和我说钓上来的不是鲑鱼的概率是0.40是一样的意思。
这个公式告诉我们,如何在得到新的数据后更新我们先前关于某个假设的信念。在这个公式中,P(H)是在收集数据前,焦点假设正确的概率估计值;P(~H)是在收集数据前,备择假设是正确的概率估计值。另外,其中还有一些条件概率,如P(H/D)表示得到实际观察到的数据特征后,焦点假设成立的概率(有时也叫作“后验概率”);P(D/H)是如果焦点假设是正确的,能够观察到这种特定数据特征的概率;P(D/~H)(我们之后将见到,一个非常重要的数值)是在备择假设成立的情况下,观察到这种特定数据特征的概率。需要意识到,P(D/H)和P(D/~H)不是互补的关系(相加不为1)。在给定焦点假设和备择假设的情况下,某种数据特征都可能出现也可能不出现。
人们在更新信念时经常不能完全遵从贝叶斯规则的要求。我们将在本章后面的部分看到反映这种情况的一些例子。不过,还需要再强调一下,准确地计算出概率的数值并不是我们在本章中所要强调的,得到正确估计值的一个恰当理念范围才是最重要的。我们并不强求正确的运算方法,而是想让读者体会这种贝叶斯式的思维。