




黑洞被发现会自转和脉动,
它贮藏能量,
也释放能量,
而且没有毛
那是1975年,在芝加哥城南部密歇根湖畔的芝加哥大学,在一间俯瞰56号大街的办公室里,钱德拉塞卡正埋头发展黑洞的完备的数学描述。他这时分析的黑洞,与60年代初物理学家刚开始把握黑洞概念时的那些怪物有根本的不同。这中间的10年,是黑洞研究的黄金年代,是我们改变对广义相对论预言的认识的年代。
在黄金年代开始的1964年,黑洞被顾名思义地认为是空间中物体可以落进却没有东西可以出来的一个洞。但在黄金年代里,经过100多位物理学家用爱因斯坦广义相对论进行的一次又一次计算,这种图像已经改变了。现在,当钱德拉塞卡坐在芝加哥办公室里计算的时候,黑洞不再被认为仅仅是一个静悄悄的洞,而是一个活动的物体:黑洞会旋转,旋转时,在它周围的弯曲时空里会产生龙卷风一样的涡旋运动。在旋涡中应该贮藏着大量的能量,自然可以开发这些能量,用它作为宇宙爆炸的动力。当恒星、行星或小黑洞落进大黑洞时,能量会使大黑洞脉动,大黑洞的视界会内外波动,像地震后地球表面上下振动一样。这样的脉动将产生引力波——在宇宙空间向外传播的时空曲率的微澜,带着黑洞和谐的乐音。
黄金年代出现的最大惊奇,也许是广义相对论坚信黑洞的所有性质都能用三个参数来预言:黑洞的质量、旋转速度和电荷。如果谁有足够的数学素养,他就能根据这三个参数进行计算。例如,他可以计算黑洞视界的形状,引力作用的强度,周围时空涡旋的细节和脉动的频率。到1975年,多数性质我们都知道了,但还不是全部。认识黑洞剩下的性质是艰苦的挑战,正好也是钱德拉塞卡喜欢的那类挑战,为了自己的追求,他在1975年接受了挑战。

1971年秋,钱德拉塞卡与研究生特奥科尔

1975年夏,在普林斯顿大学参加会议为黑
在近40年的时间里,30年代与爱丁顿论战的痛苦一直郁积在钱德拉塞卡内心,他没能回到大质量恒星的黑洞命运的研究上来。在这40年里,他为现代天体物理学做出了许多基础性的贡献——关于恒星及其脉动的,关于星系的,关于星际气体云的以及关于许多其他方面的。但总的说来,大质量恒星的命运在诱惑着他,他终于在这个黄金年代从痛苦中摆脱出来了。
他回到了多数是学生和博士后的研究大家庭。黄金年代是年轻人的,他们欢迎钱德拉塞卡来到他们中间,他虽已人到中年而且行为保守,却还有颗年轻的心。在长期访问加州理工学院和剑桥大学时,他常去自助食堂,周围都是轻松随便、穿戴漂亮的研究生,而他却穿着一身暗淡的灰衣服——年轻的朋友说这种颜色是“钱德拉灰”。
黄金年代是短暂的。加州理工学院的研究生普雷斯(Bill Press)曾为黄金年代命了名,而在1975年夏当钱德拉塞卡开始计算黑洞性质时,普雷斯却忙着它的“葬礼”:筹划在普林斯顿大学召开一个为期4天的只请30岁以下的研究者参加的会。
 会上,普雷斯和他的年轻同事们一致认为,现在是转向研究其他课题的时候了。黑洞作为旋转、脉动的动态天体的图像已大概勾画出来,而理论发现的步子开始慢下来了。所有剩下的事情似乎只是补些细节。钱德拉塞卡和几个人能将它画好,而他的年轻(现在长大了)朋友们寻找新的挑战去了。钱德拉塞卡并不满意。
会上,普雷斯和他的年轻同事们一致认为,现在是转向研究其他课题的时候了。黑洞作为旋转、脉动的动态天体的图像已大概勾画出来,而理论发现的步子开始慢下来了。所有剩下的事情似乎只是补些细节。钱德拉塞卡和几个人能将它画好,而他的年轻(现在长大了)朋友们寻找新的挑战去了。钱德拉塞卡并不满意。
改变我们对黑洞的认识的那些年轻人是谁?是三位杰出先生的学生、博士后和学生的学生。那三位先生是:美国新泽西州普林斯顿的惠勒(John Archibald Wheeler),莫斯科的泽尔多维奇(Yatov Borisovich Zel’dovich)和英格兰剑桥的席艾玛(Dennis Sciama)。他们通过他们的徒子徒孙,在黑洞的现代认识上留下了自己的烙印。
三个好老师,都有自己的风格。事实上,恐怕难以找到比这更鲜明的风格了。惠勒是有魅力、凭灵感的幻想家。泽尔多维奇像一个紧密团结的球队的雄心勃勃的队员和教练。席艾玛像自我牺牲的“催化剂”。在接下来的几页,我们会一个个地认识他们。
第一次与惠勒见面的情景我还记得很清楚。那是黄金年代来临两年前的1962年9月。那时,他刚相信了黑洞的概念,而22岁的我也刚从加州理工学院毕业来普林斯顿攻读博士。我很想在惠勒指导下从事相对论研究,于是惶恐地第一次敲响了他办公室的门。
惠勒教授热情微笑地招呼我,让我进了办公室,马上就开始讨论星体坍缩的奥秘(他把我看成是他尊重的同行,而不是一个十足的新手)。惠勒在谈那个年代的文章里描述了我们讨论时的心情:“在物理学史中,人们现在比过去任何时候[在星体坍缩的研究中]更有把握猜测他遇到了新现象,它有自己神秘的本性,等着人们去揭示……不论[未来研究的]结果如何,我们感到,最终会[在星体坍缩中]发现某个现象,广义相对论将在这里戏剧性地找到自己的归宿,圆满实现它与量子物理学火热的结合。”
 一个小时后我出来时,已经完全相信了。
一个小时后我出来时,已经完全相信了。
惠勒带着5到10名普林斯顿的学生和博士后——启发他们,但不具体指导。他认为我们很不错,能自己做好具体的事情。他为我们每个人提出了第一个研究问题——可能为星体坍缩、黑洞或广义相对论与量子物理学的“火热的结合”带来新发现的那些问题。如果发现第一个问题太难,他会慢慢将我们引向更容易的方向;如果问题很容易,他会鼓励我们把能认识到的东西都提出来,写一篇论文,然后去迎接更有挑战性的问题。我们很快学会了同时解决几个问题——一个太难的问题在解决之前,在有希望带来巨大回报之前,会一次又一次地走进脑海,而那些简单的问题很快就会有结果。自始至终,惠勒都只是给我们提些忠告,免得错误太多,但从来不会让我们感觉是他替我们解决了问题。
我的头一个问题很怪:拿根磁铁棒,磁场穿过它,从两端出来。场由力线组成,将铁粉洒在下面有磁铁的白纸上,谁都能看到这些力线[图7.1(a)]。相邻的力线相互排斥(将两块磁铁的北极相互推近,就能感觉这种排斥)。尽管如此,每个磁场的力线还是因为磁铁而聚在一起。把磁铁拿走,排斥会使力线爆裂(图7.1(b))。这件事情,我还在读大学时就熟悉了。在普林斯顿的惠勒办公室里与他的一次私人长谈中,他又让我想起它来。他那回讲了他的朋友,塔拉哈西佛罗里达大学的梅尔文(Mael Melvin)教授的最新发现。
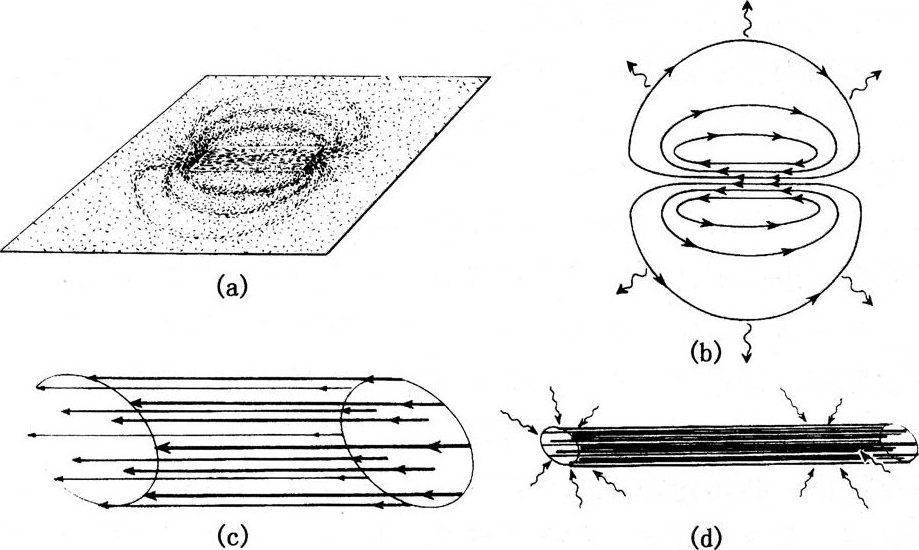
图7.1 (a)磁棒的磁力线,在磁棒上面
(b)纸和磁棒拿走后,同样的磁力线。相邻力线间的压力使它们沿箭头方向爆裂。
(c)无限长的柱状磁力线束,它的场很强,能量产生的时空弯曲(引力)足以克服力线间的排斥而将线束维系在一起。
(d)惠勒猜测,如果(c)的磁力线束收缩一点,则引力足以使线束发生坍缩(波浪线)
梅尔文发现,根据爱因斯坦场方程,磁力线不但能靠磁棒中的铁约束在一起而不会爆裂,也可以靠引力而不需要任何磁力的帮助。原因很简单:磁场有能量,而能量产生引力。[为什么能量会产生引力?回想一下,能量与质量是“等价的”(卡片5.2):任何类型的物质(铀,氢或者别的东西)都可能转变为能量;反过来,任何类型的能量(磁能、爆发能或者别的)也能转化成物质。因此,在深层意义上,质量和能量不过是同一事物的不同名称,这意味着,由于一切形式的物质都产生引力,所以一切形式的能量也必然如此。仔细检验爱因斯坦场方程就能证明这一点。]现在,假如我们有一个极强的磁场——远比在地球上遇到的强——那么,强磁场将产生强引力,而引力会压缩磁场,将磁力线约束在一起,而不管这些力线之间有多大压力[图7.1(C)]。这就是梅尔文的发现。
惠勒的直觉告诉他,这种“被引力捆绑的”磁力线可能像立在笔尖的铅笔一样是不稳定的;轻轻推一下铅笔,它会因重力而倒下。轻轻压缩磁力线,引力可能会超过压力,使力线发生坍缩[图7.1(d)]。坍缩成什么呢?也许形成一个无限长的圆柱状黑洞,也许形成一个裸露的奇点(没有视界遮蔽的奇点)。
在真实宇宙中,磁场太弱了,不可能形成足够强大的引力来反抗爆裂,不过这一点在惠勒看来是无关紧要的。惠勒追求的不是去认识存在的宇宙,而是要认识主宰宇宙的基本定律。他希望通过提出一些将定律推向极端的理想化问题,获得对这些定律的新认识。照这种精神,他为我选定了第一个引力研究的问题:试用爱因斯坦场方程来判断梅尔文的磁力线束是否会坍缩,如果会,它将坍缩成什么?
我为这个问题奋斗了好几个月。白天的战场是普林斯顿帕尔玛物理实验室的顶楼,我在那儿跟其他学物理的同学共用一间大办公室,我们一起讨论问题,互相尊重,友好和睦。晚上,回到一间小屋子,那是从第二次世界大战的士兵营房改造来的,我跟妻子琳达(画家和数学系学生)、女儿卡莱丝和我们的大柯利狗“王子”就住在这里。每天,我带着问题往返于兵营和实验楼。每过几天,就去找惠勒,请他指导。不知在纸上写了多少,在计算机上算了多少,在黑板上跟同学讨论了多少,问题终于慢慢清楚了。爱因斯坦的方程在我的穷追猛打下,终于告诉我,惠勒的猜想错了。不论用多大力量挤压梅尔文的圆柱状磁力线束,它总会反弹回来。引力永远也不可能克服磁场的排斥压力。这里没有坍缩。
这是最好的结果,惠勒热情地向我解释:当计算证实了希望,那不过是增强了一点儿对物理学定律的直觉认识。但如果计算与希望矛盾,那么我们就走上了一条通向新认识的道路。
球状星体与梅尔文的圆柱状磁力线束之间的差异是极端的,惠勒和我认识到:当球状星体非常致密时,内部引力会超过星体所能聚集的任何形式的压力。大质量球状星体的坍缩是必然的(第5章)。反过来,不论费多大力量挤压圆柱状磁力线束,不论将它的圆形截面[图7.1(d)]压得多么紧密,力线束的压力总会超过引力而将力线拉回来。圆柱状磁力线的坍缩是禁戒的,永远不会发生。
为什么球状星体和圆柱状磁场会表现得那么不同?惠勒鼓励我从每个可能的方向去探讨这个问题,答案可能会为物理学定律带来深刻的认识。但他没有告诉我该如何去探寻,我正在成为一个独立的研究者。他相信,不要他的进一步指导而发挥我自己的研究思想,对我来说是最好的。独立能培养人的力量。
从1963到1972年,黄金年代的大部分时间,我都在努力去理解球状星体与圆柱状磁场间的差异,但只能零星地做些事情。这个问题太深太难,而另外还有些更容易的问题等着我用更多的精力去研究:星体的脉动,星体在脉动时可能发射的引力波,时空弯曲对巨大星团和对它们坍缩的影响。在这些研究中,我每年都有一两次会从抽屉里拿出几本马尼拉纸的小册子,上面记着我的磁场计算。后来,我将这些计算扩大到另一种理想化的无限长圆柱状物体的计算:热气体构成的圆柱状“星”,也就是会坍缩或者既有自转同时也坍缩的圆柱状尘埃云。尽管真实的宇宙中并没有这类东西,我零星做出的关于它们的计算却逐渐带来了结果。
到1972年,真相大白了,只有当物体在所有三个空间方向,南—北、东—西、上—下,都受到压缩时(例如,球状压缩),引力才可能超过任何形式的内部压力。相反,如果物体只在两个空间方向上经历压缩(例如,圆柱状压缩使它成为一根细长的线),引力也会增大,但还大不到战胜压力的程度。很小的一点压力,不论来自热气体还是电子简并还是磁力线,都容易超过引力,使圆柱状物体向外膨胀。如果物体只在一个方向上压缩,变成一张薄饼,压力要超过引力就更容易了。
在球形、无限长圆柱形和无限延展的薄饼的情形,我的计算是明白而确定的,对这些物体,计算容易把握。更难计算的——实际上远远超出了我的能力——是有限大小的非球形物体。但从我和我年轻同学的计算得来的物理直觉告诉了我应该期待的东西。我提出了一个环猜想。

请你随便想一类物体——一颗星,一个星团,一束磁力线或别的你喜欢的东西,测量它的质量(例如,可以通过测量引力作用在轨道上行星的强度来实现),根据质量计算物体的临界周长(18.5千米乘以以太阳质量为单位的星体质量)。如果星体是球形的(实际上它不是)而且迟早会坍缩或被挤压,那么当它压缩到临界周长以下时,它会形成黑洞。假如物体不是球形的,会发生什么呢?环猜想旨在提出一个答案(图7.2)。
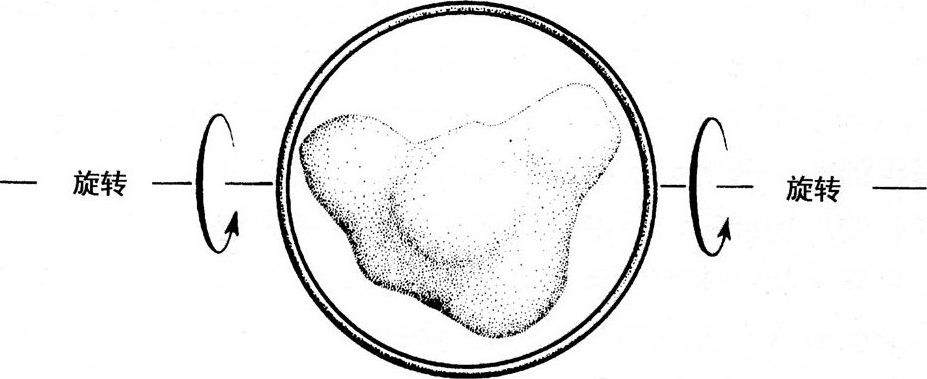
图7.2照环猜想,只有当一个具有临界周长
做一个周长等于那个物体的临界周长的环。然后,将物体放在环的中心,旋转环,看它是否能在各个方向包围物体,如果做到了,那么物体必然已经形成了一个包围自己的黑洞视界。如果做不到,那么物体还不够致密,成不了黑洞。
换句话说,环猜想讲的是,如果一个物体(一颗星,一个星团或者别的什么)经历高度非球形压缩,那么只有当它在各个方向的周长都小于临界周长时,它才会形成包围自己的黑洞。
我提出这个猜想是在1972年,从那时起,我一直在同别人一起努力,想知道它是对还是错。答案藏在爱因斯坦场方程里,但事实证明想找到答案是极其困难的。同时,支持环猜想的偶然证据不断在增多。最近,1991年,康奈尔大学的夏皮罗(Stuart Sharpiro)和特奥科尔斯基在超级计算机上模拟了高度非球形恒星的坍缩,发现包围坍缩星体的黑洞的形成完全像环猜想预言的那样。假如环能在坍缩的星体上滑动和旋转,黑洞就可以形成;如果不能,就没有黑洞。但他们只模拟了几个具有特殊非球对称形状的星体,所以在我提出环猜想近四分之一世纪后,我们还是不能肯定它是否正确,不过看来它很可能是正确的。
如果说,泽尔多维奇是苏联的惠勒,那么从许多方面说,伊戈·诺维科夫(Igor Dmitrievich Novikov)就像我。1962年,当我第一次见到惠勒并在他的指导下开始我的研究生涯时,诺维科夫也第一次来到泽尔多维奇身边,成为他的研究队伍的一员。
我小时候的生活简单富裕——出生和成长在犹他州洛根市一个严格的摩门教大家庭里
 ——相比之下,诺维科夫的生活则是崎岖艰难的。1937年,伊戈两岁时,在莫斯科铁道部任高级官员的父亲在斯大林的大恐怖中被陷害、逮捕,然后(没有朗道那么幸运)被处决了。母亲活下来,但被抓进了监狱,然后被流放。伊戈是一个叔叔养大的。
——相比之下,诺维科夫的生活则是崎岖艰难的。1937年,伊戈两岁时,在莫斯科铁道部任高级官员的父亲在斯大林的大恐怖中被陷害、逮捕,然后(没有朗道那么幸运)被处决了。母亲活下来,但被抓进了监狱,然后被流放。伊戈是一个叔叔养大的。
60年代初,我在加州理工学院学物理,伊戈是莫斯科大学的物理学研究生。
1962年,我准备去普林斯顿读研究生,跟惠勒研究广义相对论,加州的一个教授告诫我,不要学那门课。广义相对论与真实宇宙没多大关系;应该在别的地方寻找有趣的物理学挑战。(那个年代,普遍都在怀疑黑洞,没多少人对它有兴趣。)这个时候,伊戈在莫斯科以广义相对论的专题研究成了博士,他夫人诺娜也是物理学家,朋友告诫她,相对论是逆流,与真实宇宙无关。为了前途,她丈夫应该离开它。
我对那些告诫满不在乎,还是赶到了普林斯顿。而诺娜却很担心,她利用在爱沙尼亚开物理学会议的机会,向著名物理学家泽尔多维奇征求意见。她找到泽尔多维奇,问他广义相对论是不是很重要。泽尔多维奇坚决有力地回答她,相对论对天体物理学研究来说,将变得极端重要。接着,诺娜介绍了她丈夫正在研究的一个思想:星体形成黑洞的坍缩可能类似于我们宇宙的大爆炸起源,只不过时间倒转往回流了。
 诺娜讲着,泽尔多维奇越听越高兴,他自己有过同样的想法,而且还在探讨。
诺娜讲着,泽尔多维奇越听越高兴,他自己有过同样的想法,而且还在探讨。
几天后,泽尔多维奇闯进了诺维科夫和许多同学在莫斯科大学史特恩堡天文研究所的办公室,一进门就向诺维科夫追问他的研究。他们尽管思想相同,但研究方法全然不同。诺维科夫已经是相对论大家了,他用了一种巧妙的数学计算来说明大爆炸与星体坍缩之间的相似性。泽尔多维奇不太了解相对论,他靠的是深刻的物理学洞察,而计算很粗。泽尔多维奇意识到,在这儿遇到跟他一样的天才了。那时候,他刚从核武器的发明者和设计者的生命中走出来,正要组建一支新的研究队伍来研究他新发现的天体物理学。作为广义相对论的大师,诺维科夫自然是理想的队员。

左,惠勒,约1970年。右,诺维科夫和泽

席艾玛,1955年。[席艾玛提供]
诺维科夫在莫斯科大学很快乐,不太想跟他走,泽尔多维奇只好施压了。他找到应用数学研究所(他的队伍要在这儿集中)所长克尔迪什(Mstislav Keldysh),克尔迪什给莫斯科大学校长彼得洛夫斯基(Ivan Petrovsky)打电话,彼得洛夫斯基请来诺维科夫。诺维科夫惶恐地走进校长的办公室,他从没想过会走进这个高居校园中心大楼的办公室。彼得洛夫斯基很坚决:“也许你现在不想离开学校去跟泽尔多维奇工作,但你会想去的。”
 诺维科夫同意了,尽管会遇到一些困难,但他从没后悔过。
诺维科夫同意了,尽管会遇到一些困难,但他从没后悔过。
泽尔多维奇作为年轻天体物理学家的老师,作风还是他在核武器设计小组工作时形成的:“泽尔多维奇点火,队员加油”——当然,偶尔也会有别的组员闪出新的思想火花(如在相对论研究中,诺维科夫经常如此)。然后,泽尔多维奇会热情地将年轻同事的观点拿给队员们认真辩论,让它很快成熟起来,成为他自己和发现者共享的财富。
诺维科夫生动讲述了泽尔多维奇的风格。他用名加简称的姓来称呼他的老师(在俄语中,这种称呼显得尊重而亲切),他说:“雅科夫·波里希常在早晨五六点钟打电话叫醒我,‘我有了一个新想法!一个新想法!快到我房间来,我们谈谈!’我去了,常常要谈很长很长的时间。雅科夫·波里希认为我们也都能像他那样长时间地工作。他和队员们常从早晨6点到10点讨论一个题目,然后换另一个题目,讨论到中午。午餐后,大家散散步,做做操,或者打个盹。喝点儿咖啡后,又更激烈地争论到五六点钟。晚上,大家自由了,可以算点儿东西,想点儿问题或者写点儿什么,为明天做好准备。”

泽尔多维奇在设计核武器时养成了坏毛病,一贯要别人跟他走:照他的时间表,他工作时别人也工作,他睡觉时别人也睡觉。(1968年,惠勒、萨哈洛夫和我在苏联南端的一家旅馆的房间里跟他讨论了一个下午的物理学。激烈讨论几个小时后,泽尔多维奇突然宣布该睡会儿觉了。然后他躺下来睡了20分钟,惠勒、萨哈洛夫和我也轻松了,各人在房间角落里静悄悄地看书,等着他起来。)
泽尔多维奇可没耐心做像我这样的完美主义者,他不在乎一定要把所有计算细节都弄对,他只关心主要概念。他能像奥本海默那样,将无关紧要的事情抛开,集中在关键问题上,而且几乎不会出错。他在黑板上画几个箭头,几条曲线,一个不到半行的方程,几句生动的点评,就把队员引到了研究问题的核心。
他能很快判断一个思想或一个物理学家的价值,却很难改变自己的判断。一个轻率的错误判断,他能坚持好多年,这常常使他看不到重要的事实。他不相信微小黑洞会蒸发,就是这样一个例子(第12章)。但如果他的迅速判断是正确的(通常是这样),它们会使他大踏步地走向知识的前沿,比我见过的任何人都更快。
泽尔多维奇与惠勒是截然不同的。泽尔多维奇以他自己源源不断的思想和与队员们共同发展起来的思想,凭着严格的管理来塑造他的队伍。惠勒为他羽翼未丰的学生提供的是一种哲学氛围,让他们感觉到处都有思想,正等着他们去采撷。但是他从不参加学生们的讨论。惠勒的最高目标是学生的教育,不在乎拖慢了他发现的步伐。而泽尔多维奇还像在超弹计划里那样,不惜多大代价也要尽可能赶在前头。
泽尔多维奇老爱在大清早可恶地打电话把别人吵醒,要人家注意他,跟他谈论,赶快往前走。惠勒在我们学生看来是世界上最忙的人,忙着他自己的计划而把我们忘了。不过,当我们需要他的指导、智慧和鼓励时,总能找到他。
那个年代的第三位良师席艾玛的风格又与众不同。60年代和70年代初,他大部分精力都用来为他的剑桥大学的学生营造一个理想的成长环境。因为他把个人研究放在第二位,所以他比那些学生还落后,总没能升为堂堂的剑桥教授(比美国的教授地位更高)。获得奖励和荣誉的更多是他的学生。到70年代末,他原来的学生霍金(Stephan Hawking)和里斯(Martin Rees)成了剑桥教授。
席艾玛是催化剂,他让学生密切接触物理学最重要的新发现。每当一个有意义的发现发表了,他都让学生去阅读,并向别人报告。每当伦敦有什么精彩的演讲,他都会带着周围的学生或让他们坐火车去听。他有很敏锐的感觉,知道哪些思想有意义,什么问题值得探索;启动研究计划该读什么书,寻求技术指导该找哪些人。
一种忘我的渴望驱动着席艾玛去认识宇宙是如何构造的。他自己说这个驱动是一种形而上学的焦虑。宇宙似乎太疯狂,太怪异,也太迷人,接近它的惟一途径是想办法认识它,而认识它的最佳路线是依靠他的学生。让学生解决最艰难的问题,他可以比自己停留在这些问题上更快地走向下一个问题。
黄金年代的一大发现是“黑洞无毛”。科学中,有些发现是个人很快完成的,有些发现较慢,是许多研究者多方面贡献的结果。黑洞无毛属于第二种。它是三位大师泽尔多维奇、惠勒和席艾玛的学生们和其他许多人研究的产物。在接下来的几页里,我们会看到,无数研究者一步步地建立起黑洞无毛的概念,然后证明它、把握它的意义。
“黑洞无毛”的第一个线索1964年来自金兹堡,他曾为苏联氢弹发明了LiD(氘化锂)燃料,因为妻子有参与谋害斯大林的嫌疑,他没能进一步参加氢弹设计工作(第6章)。加州理工学院的天文学家刚发现类星体,宇宙最遥远的一种奇异的爆发天体时,金兹堡正在研究类星体的能源从哪儿来(第9章)。他想,一种可能是来自磁化的超大质量恒量形成黑洞时的坍缩。这种恒星的磁力线具有图7.3(a)上面所示的形状,也就是地球磁力线的形状。金兹堡猜想,恒星坍缩时,磁力线会被强烈压缩,然后猛烈爆炸,放出巨大能量。这可能有助于解释类星体。
通过计算星体坍缩的全部细节来检验这个猜想,是极端困难的,因此金兹堡走了另一条路,完成了他的第二大发现。他像奥本海默第一次粗略计算恒星坍缩所发生的事情一样,检验了一个静态恒星序列,序列中的恒星一个比一个紧密,而且穿过内部的磁力线数目都一样多。金兹堡认为,这个静态恒星序列应该能够模拟一颗单独的恒星。他导出了描述序列中每颗恒星的磁力线形状的公式,发现了令他大吃一惊的事情。当恒星接近临界周长开始形成包围自己的黑洞时,引力将把磁力线吸到恒星表面,使它紧紧贴在表面上。黑洞形成后,被吸附的磁力线就都落进视界了,没有留下能伸到洞外的[图7.3(a)]。这对金兹堡的类星体动力思想并不是好消息,但确实提出了一种有趣的可能:磁化星体坍缩成黑洞时,黑洞仍然可能像根本没有磁场那样诞生。


左:发现第一个“无毛猜想”证据的金兹堡
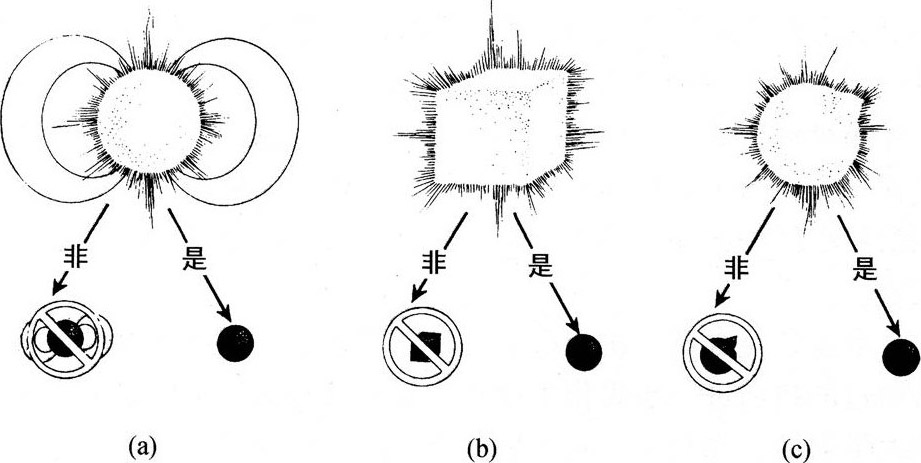
图7.3“无毛猜想”的几个例子:(a)磁
大约在金兹堡发现的同时,在几千米外的莫斯科,泽尔多维奇的研究小组——诺维科夫和多罗什克维奇(Andrei Doroshkevich)领头——开始问自己:“圆恒星坍缩形成圆黑洞,那么变形的恒星会产生变形的黑洞吗?”举一个极端例子,方形星产生方形洞吗?[图7.3(b)]。计算假想的方形星的坍缩是很困难的,于是多罗什克维奇、诺维科夫和泽尔多维奇找了一个更容易的例子:表面上隆起一座小山的近球状恒星在坍缩后形成的黑洞视界面上也会有隆起的小山吗?这样提问,计算就大大简化了,他们可以用惠勒和他的博士后雷吉(Tullio Regge)在几年前发展的一种叫微扰方法的数学技术。在卡片7.1中对这种技术作了一点解释,它是为了研究其他球对称情形的微小扰动而提出的。泽尔多维奇小组的恒星上隆起的小山所产生的引力变形,正是这种扰动。
多罗什克维奇、诺维科夫和泽尔多维奇还用奥本海默和金兹堡用过的技巧进一步简化了计算:他们没有去模拟山星的完全的动力学坍缩,而只是检验了后一个比前一个更紧密的静态山星序列。利用这个技巧和微扰方法,经过激烈争论,他们很快发现了一个显著的结果:当静态山星小到足以形成包围自己的黑洞时,黑洞视界必然是圆的,没有隆起的小山[图7.3(c)]。

类似的一个诱人的猜想是,如果坍缩的方形恒星要形成黑洞,它的视界也会是圆的而不会有棱角[图7.3(b)]。假如猜想正确,那么黑洞就不会留下什么证据来证明产生它的恒星是方的、圆的或者是有山的,而且(照金兹堡的看法),也不会有证据证明原来的恒星是磁化的还是无磁性的。
7年以后,当猜想逐渐显得正确时,惠勒发明了一个精炼的短语来描述它:黑洞无毛——“毛”说的是那些可能探出黑洞泄露形成它的原来恒星的细节的东西。
惠勒的大多数同事都难以相信,这位保守高贵的先生会知道他的短语的淫邪意思。但我怀疑他知道;我在私下里偶尔也见过他玩恶作剧。
 惠勒的词儿很快传开了,不过还有来自帕斯特纳克(Simon Pasternak)的反对。他是《物理学评论》主编,多数西方黑洞研究都发表在这家杂志。大约1971年,当伊斯雷尔想在论文中用这个词时,帕斯特纳克回信告诉他,不论什么条件下,他都决不允许这种猥亵的字眼儿出现在他的杂志上。但帕斯特纳克没能挡住滚滚而来的“无毛”论文。在法国和苏联,惠勒那个词的法语和俄语译名也是令人厌恶的,遭到了更长时间的抵制。然而,到70年代后期,这个词已经在全世界各种语言的物理学家中公开使用了,没人笑话。
惠勒的词儿很快传开了,不过还有来自帕斯特纳克(Simon Pasternak)的反对。他是《物理学评论》主编,多数西方黑洞研究都发表在这家杂志。大约1971年,当伊斯雷尔想在论文中用这个词时,帕斯特纳克回信告诉他,不论什么条件下,他都决不允许这种猥亵的字眼儿出现在他的杂志上。但帕斯特纳克没能挡住滚滚而来的“无毛”论文。在法国和苏联,惠勒那个词的法语和俄语译名也是令人厌恶的,遭到了更长时间的抵制。然而,到70年代后期,这个词已经在全世界各种语言的物理学家中公开使用了,没人笑话。
为喜欢代数的读者解释微扰方法
在代数学里,我们学过用下面的公式计算两个数a和b的和的平方:
(a+b) 2 =a 2 +2ab+b 2
假定a是一个大数,例如1 000,而相比之下b很小,例如是3,那么公式中的第3项b 2 比起其余两项来是非常小的,因而可以舍去而不会产生多大误差:
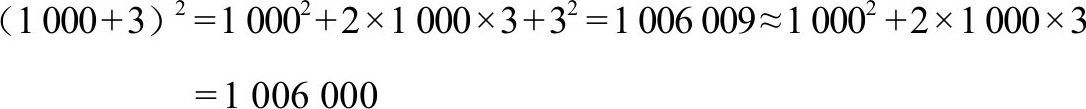
微扰方法就以这种近似为基础。a=1 000就相当于一个完全球状的恒星,b=3像恒星上的小山,而(a+b) 2 就是恒星和小山共同产生的时空曲率。计算曲率时,微扰法只保留山的特性的线性效应(如效应2ab=6 000,在b=3时是线性的);这些方法抛弃了山的所有其他影响(如b 2 =9的影响)。只要山比恒星小得多,微扰法是高度精确的。不过,假如山长得与恒星一样大(为了使恒星变成方的,就需要这样的山),那么微扰法将产生严重的误差——就像在上面的公式里a=1 000而b=1 000:
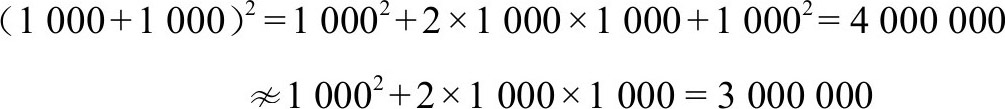
两个结果大不相同。
金兹堡、多罗什克维奇、诺维科夫和泽尔多维奇提出无毛猜想,并为它收集证据,是在1964~1965年的冬天。广义相对论专家每3年都要在世界的某个地方团聚一次,开一个星期的会,交流思想和研究结果。第4次这样的会议6月在伦敦举行。
泽尔多维奇的队员从没有走出社会主义国家的圈子,他自己当然更不行了,他刚离开核武器研究没多久。不过,诺维科夫还年轻,没进氢弹计划,他的广义相对论修养在队里是最好的(这也是泽尔多维奇招他进来的主要原因),现在成了队长(泽尔多维奇是教练),而且,他的英语虽远未精通,但也还过得去。会议当然应该选他去参加。
这是东西关系良好的时期。自斯大林12年前去世以来,苏联科学家与西方同行之间的通讯往来和相互访问逐渐在恢复。自然,现在每个重要的国际会议,苏联都会派一个小规模的科学家代表团参加,它的重要不仅在于保持苏联的科学力量,也是为了向西方科学家证明苏联的力量。自沙皇时代起,俄罗斯的官僚们在西方人面前就很自卑,现在他们可以在西方公众面前因为祖国的成就而骄傲地昂起头来。这对他们来说才是更重要的。
这样,泽尔多维奇很容易地说服了当权者让他年轻的同事诺维科夫参加苏联代表团,他已经从伦敦为他争到了一个在相对论会议上作大会报告的邀请。诺维科夫有许多激动人心的事情要报告,他将深刻地体现苏联物理学的力量。
在伦敦,诺维科夫向全世界的300名杰出的相对论物理学家作了一个小时的演说,精彩极了。关于山星引力坍缩的结果只是演说的一部分,其余部分对我们认识相对论引力、中子星、星体坍缩、黑洞、类星体本质、引力辐射以及宇宙起源,是同样重要的贡献。我坐在下面听着,被泽尔多维奇小组研究的广泛和力量惊呆了。我从没见过这样的事情。

诺维科夫讲完后,我同大家热烈地围着他,我发现我的俄语比他的英语还好一点儿,太令我高兴了,我成了讨论的翻译。人散后,诺维科夫和我一起出来,接着讨论。这样,我又多了一个好朋友。
我和大家都不可能在伦敦完全消化泽尔多维奇小组关于“黑洞无毛”的分析。细节太复杂了,我们在等着有人来为这项研究写篇文章,把那些细节认真地写出来。
1965年,用俄文写的东西传到了普林斯顿。
 我又庆幸自己曾在大学时费了好多讨厌的时间学俄语。文章分析包括两部分。第一部分,显然是多罗什克维奇和诺维科夫的工作,从数学上证明了有小山隆起的静态恒星越来越紧密时,只能产生两种结果。要么生成一个包围自己的黑洞,要么产生巨大的时空曲率。由于在恒星接近临界周长时山的影响不再是“小扰动”了,这时微扰的计算方法无效,坍缩的结果也就无从知道了。第二部分我很快知道是“泽尔多维奇式”的论证:如果山原先很小,那么从直觉看,它显然不可能在恒星接近临界周长时产生巨大的时空曲率。我们必须抛弃这种可能性。另一种可能性一定是真的:恒星必然生成一个完全球形的黑洞。
我又庆幸自己曾在大学时费了好多讨厌的时间学俄语。文章分析包括两部分。第一部分,显然是多罗什克维奇和诺维科夫的工作,从数学上证明了有小山隆起的静态恒星越来越紧密时,只能产生两种结果。要么生成一个包围自己的黑洞,要么产生巨大的时空曲率。由于在恒星接近临界周长时山的影响不再是“小扰动”了,这时微扰的计算方法无效,坍缩的结果也就无从知道了。第二部分我很快知道是“泽尔多维奇式”的论证:如果山原先很小,那么从直觉看,它显然不可能在恒星接近临界周长时产生巨大的时空曲率。我们必须抛弃这种可能性。另一种可能性一定是真的:恒星必然生成一个完全球形的黑洞。
在泽尔多维奇从直觉看来是显然的事情(最终也将证明是对的),对多数西方物理学家来说则远不是显然的。于是,争论卷进来了。
一个有争议的研究结果有很大的吸引力,就像野炊吸引蚂蚁那样。于是,泽尔多维奇小组的无毛证据把物理学家吸引过来了,先是一个一个的,然后是一群一群的。
第一个是伊斯雷尔,他生在柏林,长在南非,在爱尔兰学相对论,现在想在加拿大埃德蒙特发起一个相对论研究小组。伊斯雷尔用绝妙的数学技巧改进了那篇苏联论文的第一部分,即多罗什克维奇和诺维科夫研究的部分:他不仅像苏联人那样考虑了小山的情况,还考虑了任意形状和大小的山。事实上,他的计算对任何坍缩都是正确的,即使恒星是非球形的,甚至是方形的,而且计算还允许坍缩是动态的,而不仅是理想化的静态的恒星序列。伊斯雷尔的结论同样令人瞩目,它类似于多罗什克维奇和诺维科夫的结论,但要强得多:“一个高度非球形的坍缩只能有两个结果:要么根本不产生黑洞,要么产生完全球形的黑洞。”不过,要让这个结论正确,坍缩体必须具有两个特殊性质:它必须不带一点电荷,必须一点也不旋转。在下面我们会明白这是为什么。

伊斯雷尔第一次提出他的分析和结果是1967年2月8日在伦敦国王学院的一个演讲中。演讲很难理解,但剑桥的席艾玛却急着让学生到伦敦来听。他的学生埃利斯(George Ellis)后来回忆说,“那是一个非常非常有趣的演讲。伊斯雷尔证明了一个完全在无意中出现的定理,谁也没有想到过它,谁也没有做过这样的事情。”在伊斯雷尔快讲完的时候,米斯纳(曾是惠勒的学生)站起来提出一个猜想:如果坍缩的恒星要旋转、有电荷,会发生什么事情呢?大概也只有两种可能:或者根本没有黑洞,或者生成一个完全由坍缩星体的质量、自旋和电荷决定的具有惟一形式的黑洞。最终证明这个答案是对的,不过要等到泽尔多维奇的直觉经过检验以后。
你大概记得,泽尔多维奇、多罗什克维奇和诺维科夫曾研究过变形不大的恒星,也就是有小山隆起的近球状恒星。他们的分析和泽尔多维奇的论断引出了太多的问题。
如果坍缩恒星的表面有小山,那么坍缩的结果是什么?是山在恒星接近临界周长时产生巨大的时空曲率呢(泽尔多维奇凭直觉否决了这个结果)?还是山的影响消失而留下一个完全球形的黑洞(泽尔多维奇喜欢这个结果)?另外,如果完全球形的黑洞形成了,它用什么办法使自己摆脱山的引力影响呢?什么使黑洞成为球形的?
作为惠勒的学生,我考虑过这些问题。不过,我没有把它们作为对我的挑战,而是让我自己的学生来迎接这个挑战。那是在1968年,我在普林斯顿读完了博士又回到了母校加州理工学院,先是博士后,现在是教授了。我也学着惠勒在普林斯顿那样开始在我周围组织自己的学生队伍。
来自布鲁克林的普赖斯(Richard Price)是一个200磅重的健壮小伙子,留着粗胡须,系着黑色的空手道绸带。他跟我做过几个小项目的研究,包括运用微扰论的数学方法解决那些问题。现在他成熟了,能够承担更具挑战性的项目。泽尔多维奇的直觉的检验似乎是很理想的,但那只是一种情况。那是个热点,别的人在别的地方正在跟它斗,蚂蚁正一群群地向着野炊进攻。普赖斯得赶快去。
可惜他来晚了,别人赶到前头去了。他是第三个得到答案的,跟在诺维科夫和伊斯雷尔后面,
 但他来得更坚决,更彻底,也更有远见。
但他来得更坚决,更彻底,也更有远见。
普赖斯的远见经史密斯(Jack Smith)的笔而不朽了。史密斯是《洛杉矶时报》一个幽默的专栏作家,在1970年8月27日的《时报》上,他讲述了前一天访问加州理工学院的情景:“在教工俱乐部吃过午饭后,我独自在校园里转。我能感觉飘在空气中的深刻思想,即使在夏天,它也在吹动着橄榄树枝。我向一扇窗户看去,黑板上盖满了方程,像路上厚厚的落叶。还有三个英文句子:普赖斯的定理:能被辐射者被辐射。舒茨的观察:被辐射者能被辐射,是能被辐射者当且仅当是被辐射者。我走过窗户,好奇地想今年秋天当一年级女大学生第一次走进校园时,会给加州理工带来什么样的影响?我想,他们是不会有一点儿害羞的罢……我隐约感到,他们总会辐射出光芒的。
这段话需要一点解释。“舒茨的观察”是玩笑,而普赖斯的定理,“能被辐射者被辐射”,是彭罗斯1969年一个猜想的严格证明。
我们用山星的坍缩来说明普赖斯的定理。图7.4示意了这种坍缩。左图是第6章图6.7引进的那类时空图;右图是恒星和视界的形状在不同时刻的快照序列,最早时刻在下,最晚时刻在上。
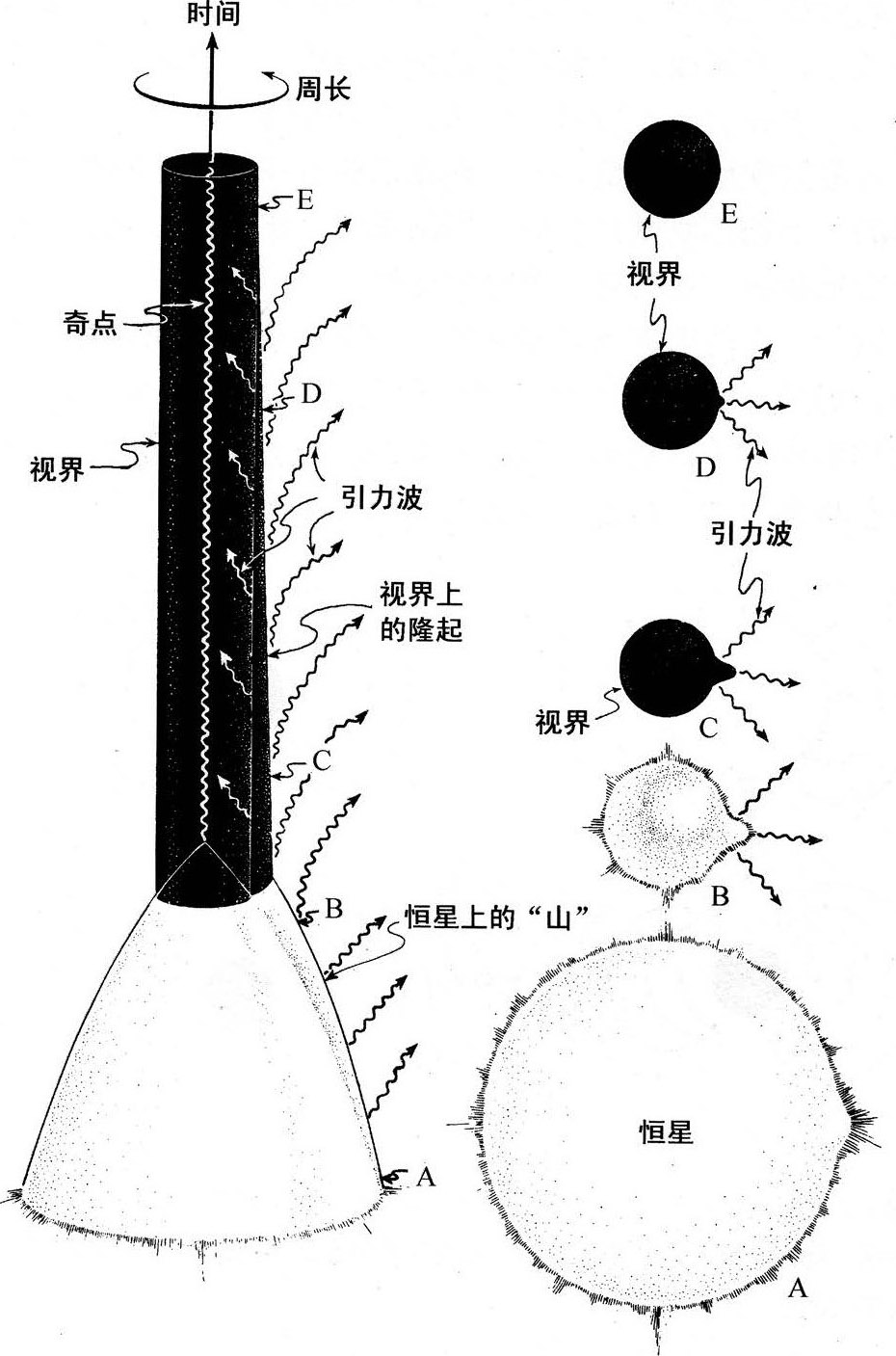
图7.4时空图(左)和快照序列(右),说
恒星坍缩时(图7.4的下面两幅快照),山越长越大,对恒星的时空曲率产生越来越强的山形扰动。然后,当恒星进入临界周长内,生成包围自己的黑洞视界时(中间那幅快照),扰动的时空曲率使视界发生形变,产生一个山形隆起。不过,这个视界的隆起坚持不了多久。产生它的星体的山这时已经沉没在黑洞以内了,所以视界不会再受它的影响,也就不再有来自山的力量使它能保持隆起。视界只能靠一种方法让隆起消失:将隆起转化为在所有方向向外传播的时空曲率的波澜(引力波——见第10章)(上面两幅快照)。有些波会落进黑洞,其余的会飞向周围的宇宙,而它们离开后,留下的就是一个完全球形的黑洞。
我们都熟悉拨动小提琴弦。只要手指将弦拉住,它就保持变形的状态;类似地,只要山突出在黑洞外,它就会令新生成的视界变形。当我们的手指离开琴弦,弦会振动,向外发出声波;声波带走琴弦变形的能量,弦回到原来的直线状态。同样,当山沉入黑洞,不能再使视界变形,黑洞振动,发出引力波;波带走视界的变形能量,黑洞处于理想的球形。
这个有山的坍缩与普赖斯的定理有什么关系呢?根据物理学定律,视界上的山形隆起能够转化为引力辐射(曲率的波动)。而普赖斯定理告诉我们,隆起一定会转化为引力辐射,这种辐射一定会将隆起完全带走。这就是黑洞无毛的机制。
普赖斯定理不仅告诉我们变形的黑洞如何失去变形,还告诉我们磁化的黑洞如何失去磁场(图7.5)。[这种情况的机制在普赖斯定理以前就由伊斯雷尔和他的两个加拿大学生德拉克鲁兹(Vicente de la Cruz)和切斯(Ted Chase)通过计算机模拟弄清楚了。
 ]磁化黑洞是磁化恒星坍缩后生成的。在视界吞食坍缩的恒星前,磁场被严格约束在恒星内部,那儿的电流使它不能逃逸。恒星被视界吞没后[图7.5(b)],磁场不能再受恒星电流影响,也就不再受它的约束。现在,它不仅可以穿过恒星,还可以穿过视界,视界是留不住它的。物理学定律允许场转化为电磁辐射(电力和磁力的波动),而普赖斯定理正好要求它那么做[图7.5(c)]。电磁辐射散开了,一部分落回黑洞,其余部分离它远去,留下一个没有磁化的洞[图7.5(d)]。
]磁化黑洞是磁化恒星坍缩后生成的。在视界吞食坍缩的恒星前,磁场被严格约束在恒星内部,那儿的电流使它不能逃逸。恒星被视界吞没后[图7.5(b)],磁场不能再受恒星电流影响,也就不再受它的约束。现在,它不仅可以穿过恒星,还可以穿过视界,视界是留不住它的。物理学定律允许场转化为电磁辐射(电力和磁力的波动),而普赖斯定理正好要求它那么做[图7.5(c)]。电磁辐射散开了,一部分落回黑洞,其余部分离它远去,留下一个没有磁化的洞[图7.5(d)]。

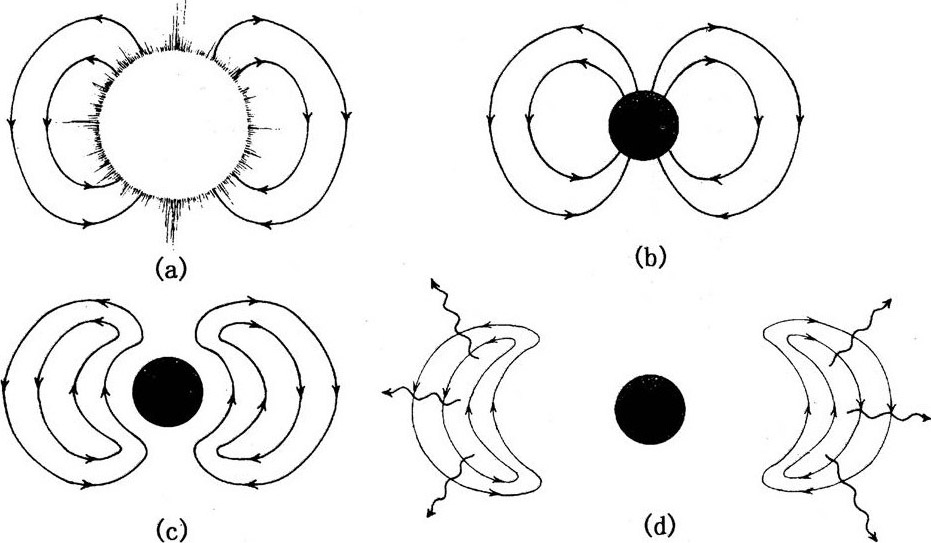
图7.5磁化恒星(a)坍缩形成黑洞
如果真像我们看到的那样,山因辐射消失,磁场因辐射而散尽,那么还能留下什么呢?什么不能转化为辐射呢?答案很简单:在物理学定律中有一类特殊的守恒律,它们肯定了某些量不可能以辐射方式振动,因此不可能转化为辐射而从黑洞附近消失。这些守恒的量是,由黑洞质量产生的引力作用,黑洞旋转产生的空间旋涡(下面讨论)和黑洞电荷产生的辐射状电力线,也就是指向洞外的电场(下面讨论)。

这样,根据普赖斯定理,在所有辐射散尽以后还能留下的,就只有黑洞的质量、自旋和电荷的影响。黑洞的其他一切特征都被辐射带走了。这意味着谁也不能靠测量黑洞最后的那些性质来揭示坍缩成这个黑洞的恒星的特征,当然,恒星的质量、自旋和电荷例外。甚至[根据惠勒的两个学生哈特尔(James Hartle)和贝肯斯坦(Jacob Bekenstein)的计算]谁也不能根据黑洞的性质来判别形成它的恒星的构成是物质的还是反物质的,是质子的还是电子的,或者是中子的还是反中子的。借惠勒的话,更准确地说,黑洞几乎无毛,它仅有的毛是质量、自旋和电荷。
最后严格证明黑洞无毛(除了质量、自旋和电荷)的并不是普赖斯。普赖斯的分析严格限制在非常接近于球形而且旋转(即使有的话)非常缓慢的恒星的坍缩,他用的微扰法需要这些限制。为认识高度变形、快速旋转的坍缩恒星,需要完全不同于微扰方法的数学工具。
席艾玛在剑桥的学生掌握着需要的工具,但是太难了,难极了。为了用这些工具完全严格地证明黑洞无毛——即使在黑洞快速旋转而且因旋转而强烈变形的情况下,它的最终性质(在所有辐射散尽以后)由质量、自旋和电荷惟一确定,席艾玛的学生们用了15年的时间。证明的大部分成绩归功于席艾玛的两个学生,卡特尔(Brandon Carter)和霍金,也归功于伊斯雷尔;但罗宾逊(David Robinson)、邦庭(Gray Bunting)和玛泽尔(Pavel Mazur)也有过重要贡献。

在第3章,我评说过我们真实宇宙的物理学定律与怀特的史诗性小说《过去和未来的国王》里蚂蚁社会的物理学定律之间的巨大差别。怀特的蚂蚁信奉“凡不被禁止的事情都是必然的”,但物理学定律大大地违背了这句箴言。许多物理学定律允许的事情实际上可能性很小而从来没有发生过。普赖斯定理则是一个显著的例外,在物理学中我还很少遇到这种情形,蚂蚁的箴言实现了:假如物理学定律并不禁止黑洞以辐射排出些东西,那么辐射也就是必然的了。
黑洞最后的“无毛”状态,同样具有异乎寻常的意义。正常情况下,物理学家为了认识我们周围复杂的宇宙,常建立一些简化的理论或计算模型。为认识天气,大气物理学家建立了地球大气环流的计算模型;为认识地震,地球物理学家建立了滑动岩体的简单理论模型;为认识恒星坍缩,奥本海默和斯尼德在1939年建立了一个简化的理论模型:一团完全均匀的、没有压力的球形坍缩的物质云。我们在建立这些模型时,完全知道它们的局限,它们不过是“真实”宇宙中“在那儿”表现出的大量复杂性的一些苍白的图画。
对黑洞来说——或者,至少当辐射散尽,带走了所有的“毛”时,情况就不同了。这时,黑洞简单极了,我们可以用简单精确的数学公式来描述它,根本用不着什么理想化。在宏观世界(也就是在大于亚原子粒子的尺度上)的任何其他地方,都不会是这样的。在其他任何地方我们的数学也不会如此精确;在其他任何地方,我们也不可能从理想化模型的局限中解脱出来。
为什么黑洞与宏观宇宙中的其他物体有那么大的不同?为什么它们(而且只有它们)会如此简单?假如我知道答案,它可能会告诉我关于物理学本质的一些更深刻的东西。可是我不知道。也许下一代物理学家会找到它。
无毛黑洞的性质是什么?广义相对论的数学对哪些性质能有那么好的描述?
如果黑洞是理想化的,绝对没有电荷和自旋,那么它正好就是我们在前些章遇到的球形黑洞,在数学上,由史瓦西1916年的爱因斯坦场方程的解来描述(第3章、第6章)。
如果电荷落进黑洞,那么黑洞获得一个新的特征:像刺猬一样辐射状向外竖立的电力线。电荷如果是正的,这些力线将从洞中把质子挤出来而吸引电子;如果是负的,力线会排斥电子而吸引质子。这类带电黑洞在数学上精确地由德国物理学家雷斯纳(Hans Reisner)和荷兰物理学家诺德斯特勒姆(Gunnar Nordstr m)分别在1916和1918年得到爱因斯坦场方程的解描述。但是,以前没人能理解雷斯纳和诺德斯特勒姆解的物理学意义。到1960年,惠勒的两个学生,格雷弗斯(John Graves)和布雷尔(Pieter Brill)才发现它描述了带电的黑洞。

苏联和西方的科学组织:对比与结果
在我和我年轻的物理学同事们努力发展环猜想,证明黑洞无毛和发现它们如何失去毛时,我们也看到,物理学的组织在苏联与在英国和美国有多么大的不同,这些差别又产生了多么深远的影响。我们的认识可能有益于某些未来计划,特别是在苏联,那儿的一切国家机构——不仅政府的和经济的,也包括科学的——现在(1993年)都正照着西方的路线重新组织。西方模式并不是完美的,而苏联的体制也不一味是坏的!
在美国和英国,不断有能干的年轻人从惠勒或席艾玛那样的研究小组中走出来。本科生可以在最后一年加入这类小组,但以后还要去读研究生。研究生可以参加3~5年,然后到另一处去读博士后。博士后两三年后要独自到另一个地方去组织自己的研究小组(如我在加州理工学院),或者加入别的研究小组。在英国和美国,不论谁有多能干,他几乎都不可能老是待在导师身边。
在苏联情形就不同了。突出的年轻物理学家(像诺维科夫)通常跟在老师身边一二十年,有的甚至三四十年。像泽尔多维奇和朗道那样的苏联大家都在科学院的研究所工作,不在大学里,教学负担很轻,有的还没有课。为了留下以前的优秀学生,他们会组织一个永久性的研究队伍,这样的队伍团结紧密,力量强大,有的可能会坚持到导师科学生涯的终点。
我的一些苏联朋友将这种差异归结为英美体制的失败:几乎所有英美大物理学家都在大学,那里通常是研究促进教学,而要建立一支强大持久的研究队伍却缺乏足够的固定职位。结果,在英国或美国都没有产生过一个像30年代到50年代的朗道小组和60年代到70年代的泽尔多维奇小组那样的理论物理学研究群体。在这个意义上,西方是没有希望同苏联竞争的。
我的一些美国朋友说这种差异是因为苏联体制失败了:在苏联,从逻辑上讲很难从一个研究所迁到另一个研究所,从一座城市迁到另一座城市,所以年轻的物理学家们只好留在老师身边;他们没有机会出去创立自己的独立研究小组。结果,批评者认为这是一种封建体制。老师像主人,而队员是他的奴隶,大部分生涯都卖给了他。主人与奴隶以复杂的方式相互依存,但谁是主人却容不得商量。如果主人是泽尔多维奇或朗道那样的大师,那么这个主人和奴隶的团队可能会产生丰硕成果。如果主人是一个独裁者而又没多大本事(通常都是这种情况),结果就惨了:糟蹋了人才。
在苏联体制下,每一个像泽尔多维奇那样的大师都只有一个研究队伍,尽管强有力,但还是不能与西方相比。不同的是,在美国或英国,像惠勒和席艾玛那样的大师会组织许多较弱小的研究队伍,分散在不同的领域,而最终都将对物理学产生重大影响。英美的导师们有源源不断的年轻人,帮助他们保持活跃的思想和头脑。苏联导师们难得重新开始,那时他们只好斩断与过去队伍的联系,可能会造成巨大的伤害。
实际上,泽尔多维奇就经历过这种事情:1961年,他开始建立他的天体物理学小组;到1964年,它成为全世界最优秀的理论天体物理学小组;后来,在1978年,黄金年代刚刚过去,这个小组就痛苦地分裂了,几乎每个组员都各奔前程,而泽尔多维奇要另走一条路,虽然在心理上也受到伤害,但他摆脱了障碍,可以自由地另辟新天地了。悲哀的是,他的重建不会成功。他不可能再有像从前他在诺维科夫协助下所带领的那么一群能干有力的队员团结在身边了。但诺维科夫现在独立了,在80年代,他成了一个重建的研究队伍的天才领导者。
我们可以用嵌入图(图7.6左)来示意带电黑洞周围的空间曲率和黑洞的电力线。这幅图与图3.4的右下图基本相同,不过恒星没有了(图3.4的黑色部分),因为它在黑洞内部而不再和外部宇宙有联系。更严格地说,本图表现了黑洞外嵌在平直三维超曲面中的赤道“平面”——黑洞空间的一个二维碎片。(这个图的意义,请看图3.3和相关正文的讨论。)赤道“平面”是从黑洞视界切下来的,所以我们只能看到黑洞的外头,而看不到里面。视界实际上是一个球面,因为我们只看它的赤道,它在图中看起来就像一个圆。图表现了辐射状指向洞外的电力线。假如从上往下看(图7.6右),我们看不到空间曲率,但确实能把电力线看得更清楚。
自旋对黑洞的影响,到60年代后期才为人们所认识,主要来自席艾玛在剑桥大学的一个学生,卡特尔。

图7.6从带电黑洞视界发出的电力线。
左:嵌入图;右:俯视嵌入图
左:R.克尔,约1975年。右
卡特尔1964年秋参加席艾玛的小组时,席艾玛很快为他提出了第一个研究问题,建议他研究真实旋转恒星的坍缩。席艾玛解释说,以前关于坍缩的所有计算都是针对理想化的非旋转恒星的,现在对付旋转效应的工具和时机看来都成熟了。一个叫克尔(Roy Kerr)的新西兰数学家刚发表了一篇文章,给出了描述旋转恒星外的时空曲率的爱因斯坦场方程的解。
 席艾玛解释说,这是从来没人发现过的第一个关于旋转恒星的解,但不幸的是,它是一个非常特殊的解,当然不能描述所有的旋转恒星。旋转的恒星有许多“毛”(许多性质,如复杂的形状和气体的复杂运动),而克尔的解几乎没多少“毛”:时空曲率的形状很光滑,很简单,简单地对应于典型的旋转恒星。不管怎么说,克尔的爱因斯坦场方程解总还是一个起点。
席艾玛解释说,这是从来没人发现过的第一个关于旋转恒星的解,但不幸的是,它是一个非常特殊的解,当然不能描述所有的旋转恒星。旋转的恒星有许多“毛”(许多性质,如复杂的形状和气体的复杂运动),而克尔的解几乎没多少“毛”:时空曲率的形状很光滑,很简单,简单地对应于典型的旋转恒星。不管怎么说,克尔的爱因斯坦场方程解总还是一个起点。
很少有研究问题像这样立刻就有了收获:一年内,卡特尔就从数学上证明克尔解描述的不是旋转的恒星,而是旋转的黑洞。[伦敦的彭罗斯、利物浦的波耶(Robert Boyer)以及林凯斯特(Richard Linquist)——过去是惠勒的学生,现在在康涅狄格米德尔顿的卫斯理大学——都独立发现了这一点。]
 到70年代中期,卡特尔和其他人又继续证明了,克尔解不仅描述了一类特殊的旋转黑洞,而且描述了所有可能存在的旋转黑洞。
到70年代中期,卡特尔和其他人又继续证明了,克尔解不仅描述了一类特殊的旋转黑洞,而且描述了所有可能存在的旋转黑洞。

旋转黑洞的物理性质充实在克尔解的数学中,卡特尔通过认识数学而发现了那些性质应该是什么。
 最有趣的是黑洞在它周围时空产生的龙卷风似的旋涡。
最有趣的是黑洞在它周围时空产生的龙卷风似的旋涡。
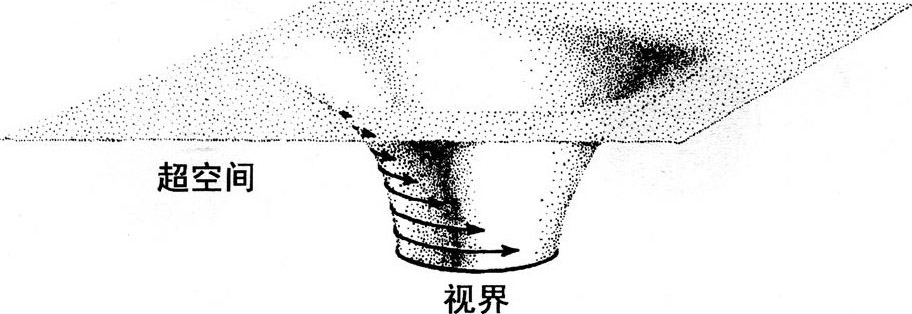
图7.7黑洞旋转在空间产生的“龙卷风旋涡
旋涡如图7.7的嵌入图,喇叭形的曲面是嵌在三维平直超曲面内的黑洞的赤道面(黑洞空间的一个二维碎片)。黑洞的旋转抓住它周围的空间(喇叭曲面)像龙卷风一样跟着它旋转,速度与图中箭头的长度成正比。在远离龙卷风中心,空气旋转慢;同样,在远离黑洞视界,空间旋转慢。在龙卷风中心附近,空气旋转快;同样,在黑洞视界附近,空间旋转快。在视界处,空间紧紧附在视界面上,以完全相同的速度跟它旋转。
空间的旋涡对落进黑洞的粒子的运动必然会产生影响。图7.8表现了两个这样的粒子径迹,图是在洞外静止观察者的参照系中看到的——也就是说观察者不落向视界进入黑洞。
第一个粒子[图7.8(a)]下落很慢。如果黑洞不旋转,粒子将像坍缩恒星的表面那样,先是越来越快地呈辐射状向内运动,然后,在洞外的静止观察者看来,它将减慢下落速度,正好在视界上冻结(回想一下第6章的“冻星”)。黑洞的旋转以非常简单的方式改变了这种情况:旋转在空间产生旋涡,空间旋涡带着靠近视界的粒子跟它一起旋转。于是,粒子被冻结在旋转的视界上,而在外面的静止观察者看来,它在绕着视界永不停息地旋转着。(同样,当旋转的恒星坍缩成旋转的黑洞时,外面的静止观察者会看到恒星表面被“冻结”在旋转的视界上,永不停息地绕着它转。)
虽然外面的观察者看到图7.8(a)的粒子冻结在旋转的视界上并永远留在那儿,但从粒子角度看,情况就大不一样了。当粒子接近视界时,由于引力的时间膨胀作用,粒子的时间与外面静止参照系的时间相比越来越慢。外面无限长的时间过去了,粒子却只经历了有限的很短的时间。在那个有限的时间里,粒子达到了黑洞的视界,在接下来的瞬间里,粒子将完全陷入视界,落进黑洞中心。下落粒子自己的经历与外面观察者看到的过程之间的这么巨大的差异,我们已经在恒星坍缩中遇到过了:从恒星表面看到的星体坍缩(快速陷入视界)与外面观察者看到的坍缩(坍缩冻结,见第6章最后部分)也是这样大不相同的。
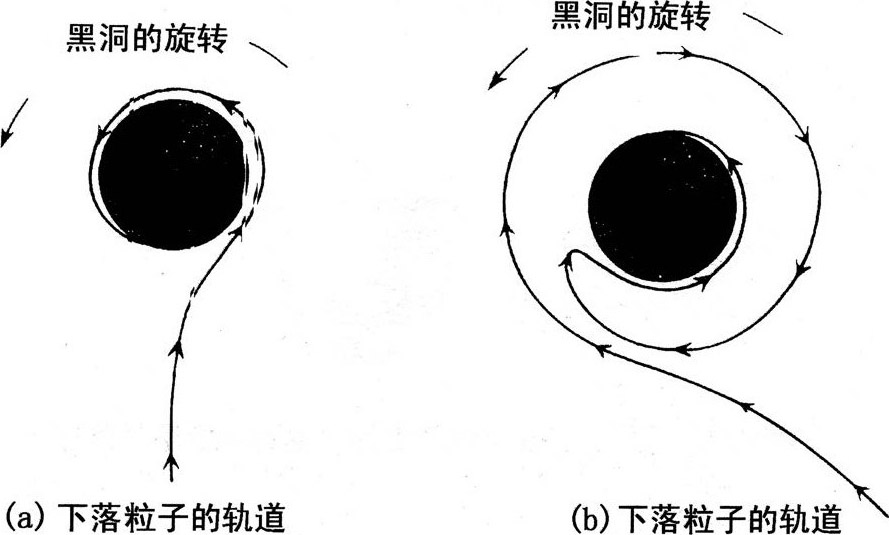
图7.8落向黑洞的两个粒子在空间的轨道
第二个粒子[图7.8(b)]是沿与黑洞旋转方向相反的螺旋轨道落下去的,但当它越来越靠近视界时,还是会被卷进空间旋涡,改变螺旋方向,在外面观测者看来,它也会像第一个粒子那样,被迫跟着视界旋转。
黑洞的旋转除了在空间产生旋涡,还会使视界产生变形,就像地球自转使地球表面产生变形一样。离心力会将旋转的地球赤道相对于两极向外拉出22千米。同样,黑洞的视界的赤道也会因离心力作用而像图7.9画的那样向外凸起。假如黑洞没有旋转,它的视界将是球形的(左图)。假如黑洞旋转很快,凸起就会很大(右图)。
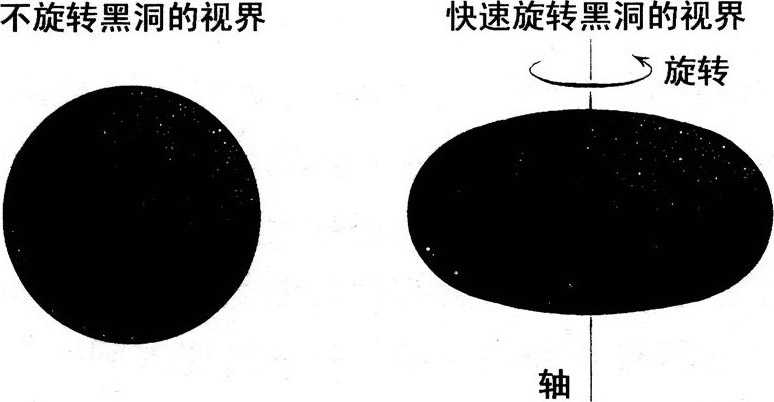
图7.9两个黑洞视界的形状,一个不转(左
假如黑洞会急速地旋转,离心力会将视界撕裂开来,就像急速旋转的水桶将桶里的水抛洒出来。于是,存在某个能让黑洞存在的极大旋转速度。图7.9右边的黑洞在以这个极大值的58%的速度旋转。
那么,能让黑洞比允许的最大速度旋转更快一些吗?那样,它的视界会被破坏,而我们可以管窥它的内部。很遗憾,我们做不到。在1986年,也就是黄金年代过去10年后,伊斯雷尔证明了,不论用什么方法,想让黑洞比极大速度转得更快,总是要失败的。
 例如,如果谁想通过向黑洞投进一些旋转更快的东西来提高以极大速度旋转的黑洞的速度,离心力会阻止快速旋转的物质到达视界进入黑洞。另外,也许急速旋转的黑洞与周围宇宙的小小随机相互作用(例如,远处恒星的引力作用)还会使旋转变慢一点。看来,物理学定律不想让黑洞外面的人偷看它的内部,不想让他发现藏在黑洞中心的奇点的量子引力秘密(见第13章)。
例如,如果谁想通过向黑洞投进一些旋转更快的东西来提高以极大速度旋转的黑洞的速度,离心力会阻止快速旋转的物质到达视界进入黑洞。另外,也许急速旋转的黑洞与周围宇宙的小小随机相互作用(例如,远处恒星的引力作用)还会使旋转变慢一点。看来,物理学定律不想让黑洞外面的人偷看它的内部,不想让他发现藏在黑洞中心的奇点的量子引力秘密(见第13章)。
像太阳质量的黑洞,极大旋转速率是0.000 062秒(62微秒)一周。因为这个黑洞的周长大约是18.5千米,所以对应的转速是18.5千米/0.000 062秒,大约等于光速,299 792千米/秒(这完全不是巧合)。质量为100万个太阳的黑洞,周长是太阳质量黑洞的100万倍,所以它的极大旋转速率(使它以光速转动的速率)就要小100万倍,即62秒转一圈。
1969年,彭罗斯(在第13章我们会更多地认识他)有一个惊人发现。
 通过巧妙处理克尔的爱因斯坦场方程解,他发现旋转的黑洞在周围空间旋涡里藏着旋转能,因为旋涡和它的能量都在黑洞视界之外,所以这种能量实际上是可以用来作能源的。彭罗斯的发现了不起,因为黑洞的旋转能是巨大的。如果黑洞以极大速率旋转,它贮藏和释放能量的效率将比太阳所存的核燃料还高48倍。如果太阳在整个一生中燃尽全部核燃料(实际上是燃不尽的),也只有0.006的质量转化为光和热。如果去提取一个快速旋转黑洞的所有旋转能(这样会使它停下来),我们可以得到相当于48×0.006=29%黑洞质量的可利用能量。
通过巧妙处理克尔的爱因斯坦场方程解,他发现旋转的黑洞在周围空间旋涡里藏着旋转能,因为旋涡和它的能量都在黑洞视界之外,所以这种能量实际上是可以用来作能源的。彭罗斯的发现了不起,因为黑洞的旋转能是巨大的。如果黑洞以极大速率旋转,它贮藏和释放能量的效率将比太阳所存的核燃料还高48倍。如果太阳在整个一生中燃尽全部核燃料(实际上是燃不尽的),也只有0.006的质量转化为光和热。如果去提取一个快速旋转黑洞的所有旋转能(这样会使它停下来),我们可以得到相当于48×0.006=29%黑洞质量的可利用能量。
奇怪的是,为了寻找一种大自然可能用来攫取和利用黑洞旋转能的可行办法,物理学家还费了7年的时间。他们找了一个又一个古怪的办法,在原则上都是可能的,但在最后发现自然的精灵前,没有哪个办法显得有多大的实用希望。我将在第9章讲这些寻找和发现,结果是,一个黑洞“机器”为类星体和巨大喷流提供了能源。
我们已经看到电荷产生指向黑洞视界外的辐射状电力线,旋转在黑洞周围空间产生旋涡,使黑洞形状发生扭曲,在旋涡中贮藏能量,那么,如果黑洞既有电荷又有自旋,会发生什么呢?不幸的是,答案没多大意思,什么新东西也没有。黑洞电荷产生通常的电力线,自旋产生通常的空间旋涡,贮藏旋转能量,使视界赤道以通常方式隆起。惟一新奇的事情是,空间旋涡在流过电场时会产生一些没多少意义的磁力线。(这些力线不是黑洞的新“毛”,不过是旧的标准形式的毛的相互作用的一个表现:自旋产生的旋涡与电荷产生的电场之间的相互作用。)旋转的带电黑洞的一切性质都体现在1965年得到的爱因斯坦场方程的一个精妙的解中,得到这个解的是皮兹堡大学的纽曼(Ted Newman)和他的一群学生:科赫(Eugcne Couch)、金纳帕尔(K.Chinnapared)、埃克顿(Albert Exton)和托伦斯(Roberlt Torrence)。

黑洞不仅能旋转,还会脉动。不过,脉动是旋转发现近10年后才在数学上发现的,发现途中曾遇到过一块巨大的拦路石。
惠勒的学生们“观察”了3年(1969~1971)的黑洞脉动,却不知道在看什么。这些学生有普赖斯(我的学生,也就是惠勒的徒孙)、维什维西娃拉(C.Y.Vishveshwara)和埃德尔斯坦(Lester Edelstein,马里兰大学米斯纳的学生,也是惠勒的徒孙),以及泽雷里(Frank Zerilli,惠勒自己在普林斯顿的学生)。他们借助计算机模拟和纸上计算观察黑洞的脉动。他们认为自己看到的是引力波(时空曲率的波动),在黑洞附近反弹,又被黑洞自身的时空曲率捕获,但捕获不彻底,波动慢慢地从黑洞附近漏出来,然后飞散。这个想法不错,但没什么意思。1971年秋,我的小组里的新研究生普雷斯意识到,时空曲率波动在黑洞附近的回弹可以想象为黑洞自身的脉动。毕竟,从视界以外看,黑洞除了时空曲率外什么也没有。所以,曲率的波动也只能是黑洞曲率的脉动,从而也就是黑洞本身的脉动。

这一观点的改变产生了巨大影响。如果认为黑洞能够脉动,我们自然要问,它们与铃铛的脉动(“响铃”)或恒星的脉动有哪些相似?在普雷斯以前,没人问过这类问题;以后,这些问题就很显然了。
铃和星都有一个脉动的自然频率。(铃的自然频率产生纯粹的铃响音调。)那么,黑洞也有类似的自然脉动频率吗?是的,普雷斯通过计算机模拟发现了。这个发现激发了钱德拉塞卡和德维勒(Steven Detweiler,惠勒的学生的学生)开始对所有黑洞的自然脉动频率进行编目,在第10章,我们会回来谈这些频率,也就是黑洞的“铃声”。
快速转动的车轮稍微偏离正轨时,会产生振动,振动从旋转获得能量,越来越强烈。实际上,振动可以达到非常强烈的地步,在极端情况下,甚至可以使车轮脱离汽车。物理学家说“车轮振动是不稳定的”。普雷斯知道这一点,也知道旋转恒星有类似的现象。所以当他发现黑洞会脉动时,自然要问,“假如黑洞旋转很快,它的脉动会稳定吗?它们会从黑洞的旋转中获取能量,然后用这些能量来加强脉动吗?脉动会强烈到撕裂黑洞的地步吗?”钱德拉塞卡(那时对黑洞研究还不够深入)认为会的,我想不会。1971年11月,我们打了个赌。
判决输赢的工具那时还不存在。需要什么工具呢?由于脉动刚开始很弱,慢慢才会加强(如果能加强的话),可以认为它是黑洞时空曲率的“微扰”——就像敲响的酒杯的振动,是对酒杯形状的小小扰动。这意味着黑洞的脉动可以用卡片7.1中大概介绍过的微扰方法来进行分析。不过,普赖斯、普雷斯、维什维西娃拉、钱德拉塞卡和其他一些人在1971年秋所用的具体的微扰方法却只适用于非旋转或旋转很慢的黑洞。为了快速旋转的黑洞的扰动,他们需要一种全新的微扰方法。
设计这种方法,成了1971年和1972年的热点问题。我的学生,米斯纳的学生,惠勒的学生以及钱德拉塞卡和他的学生弗里德曼(John Friedman)像其他人一样都在为它工作。竞争很激烈,特奥科尔斯基赢了,
 他是我的一个南非学生。
他是我的一个南非学生。

1972年12月在纽约Mama
特奥科尔斯基生动回忆了他那个微扰法的方程清晰出现的情景:“有时当你在搞数学的时候,你的头脑就开始模式选择了。”他说,“1972年5月的一个晚上,我正坐在我们在帕萨迪纳公寓的厨房的桌旁弄数学;妻子罗茜在特弗龙平底锅上煎薄饼,原想它不粘锅,但还是粘了。每次她会倒些奶油面糊进去,在桌上敲锅,一边骂,一边敲,我大声喊她安静些,因为我正兴奋着;在我的数学公式中,一项项都相互抵消了,所有的东西都消失了!方程清晰出现了!我坐在那儿盯着那些惊人简单的方程,一心在想,我有多笨!6个月前就该发现它们了;我现在做的不过是把正确的东西加到一起。”

用特奥科尔斯基方程,可以分析所有类型的问题:黑洞脉动的自然频率,黑洞脉动的稳定性,中子星被黑洞吞没时发出的引力波以及更多的其他问题。斯塔洛宾斯基(Alexi Starobinsky,泽尔多维奇的学生)、瓦尔德(Bob Wald,惠勒的学生)和科恩(Jeff Cohen,惠勒的学生布雷尔的学生)的研究小组和其他许多人很快就进行了这些分析,推广了特奥科尔斯基的方法。特奥科尔斯基和普雷斯在把握最重要的问题:黑洞脉动的稳定性。

他们通过计算机计算和公式计算导出的结论令人失望:不论黑洞旋转多快,脉动都是稳定的。
 黑洞脉动的确要从洞中攫取旋转能量,但它们也通过引力波辐射能量;而辐射能量的速率总是大于从黑洞的旋转中获得能量的速率。因此,脉动能总会消失,脉动永远不会增强,从而黑洞不可能被脉动破坏。
黑洞脉动的确要从洞中攫取旋转能量,但它们也通过引力波辐射能量;而辐射能量的速率总是大于从黑洞的旋转中获得能量的速率。因此,脉动能总会消失,脉动永远不会增强,从而黑洞不可能被脉动破坏。
因为普雷斯和特奥科尔斯基的结论关键靠的是计算机计算,钱德拉塞卡不满意,不承认打赌输了。只有直接通过公式做出了完整的证明,他才会完全信服。15年后,霍金以前的博士后怀庭(Bernard Whiting,也就是席艾玛的徒孙)给出了这样的证明,钱德拉塞卡认输了。

钱德拉塞卡比我更喜欢完美。在完美主义者的名单上,他和泽尔多维奇各占一端。1975年,当黄金年代的年轻人宣布黄金年代结束了,所有的人都离开黑洞研究时,钱德拉塞卡很苦恼。这些年轻人掌握的特奥科尔斯基的微扰法足以证明黑洞可能是稳定的,但他们没有为这些方法带来恰当的形式,让其他物理学家能够自行计算任何可能的黑洞扰动的所有细节——如脉动,来自下落中子星的引力波,黑洞炸弹或其他。他们的半途而废令人心痛。
于是,1975年,65岁的钱德拉塞卡把卓越的数学才能都用到了特奥科尔斯基的方程上。凭着用不完的精力和深刻的洞察,他穿过缤纷的数学丛林,将采撷的花朵织成一幅“洛可可式”的图画:
 “华丽,壮观,赏心悦目。”1983年,他在73岁时终于完成了使命,发表了题为《黑洞的数学理论》的著作——这是未来10年黑洞研究者的数学手册,他们能想到的任何黑洞微扰问题都能从这本手册中找到解决的办法。
“华丽,壮观,赏心悦目。”1983年,他在73岁时终于完成了使命,发表了题为《黑洞的数学理论》的著作——这是未来10年黑洞研究者的数学手册,他们能想到的任何黑洞微扰问题都能从这本手册中找到解决的办法。
