




爱因斯坦的卷曲时空定律
预言了黑洞,
爱因斯坦拒绝了这个预言
“至于为什么‘史瓦西奇点’不存在于物理学实体中”,1939年,爱因斯坦在一篇论文中写道,“这个考察的基本结果说得很清楚了。”
 爱因斯坦用这句话明确地拒绝了他自己的理性财产:他的广义相对论引力定律似乎正在预言的黑洞。
爱因斯坦用这句话明确地拒绝了他自己的理性财产:他的广义相对论引力定律似乎正在预言的黑洞。
那时,根据爱因斯坦的定律还只能得到黑洞的几个性质,而“黑洞”这个名字也还没有,它们被称为“史瓦西奇点”。不过,人们已经明白,落入黑洞的任何事物不可能再逃出来,也不可能发出光或其他东西,而这已经足以让爱因斯坦和他那个时代的大多数物理学家相信,黑洞是可怕的怪物,肯定不会存在于真实宇宙中。物理学定律一定会以某种方法使宇宙不受这种怪物的侵害。
爱因斯坦如此强烈地拒绝黑洞,那么,关于黑洞,他们那时都知道些什么呢?广义相对论关于黑洞存在的预言有多大力量?爱因斯坦怎么能拒绝这个预言而仍然相信他的广义相对论的定律呢?这些问题的答案有着18世纪的渊源。
在整个18世纪,科学家(那时叫自然哲学家)们相信,引力服从牛顿定律,光由光源以极高的普适速度发出的微粒(粒子)组成。通过望远镜对木卫在绕木星的轨道上所发出的光的测量,知道光速大约是每秒300 000千米。
1783年,英国自然哲学家米歇尔(John Michell)大胆地将光的微粒描述与牛顿的引力定律结合,从而预言了非常致密的星体应该是什么样的。
 我把他的思想实验换个说法重复一遍。
我把他的思想实验换个说法重复一遍。
在一颗星体的表面,以某初始速度抛出一个粒子让它自由向上运动。如果初始速度太低,星体引力将减慢粒子速度,使它停下来,然后将它拉回星体表面。如果初始速度足够大,引力也将使粒子慢下来,但不会使它停止,粒子将设法逃掉。回落与逃逸的界线,即为了逃逸的最小初始速度,叫“逃逸速度”。对从地球表面抛出的粒子来说,逃逸速度是每秒11千米,从太阳表面抛出的粒子,逃逸速度为每秒617千米,或光速的0.2%。
米歇尔能用牛顿的引力定律计算逃逸速度,证明它正比于星体质量除以其周长的平方根。因此,对质量一定的星体来说,周长越小,逃逸速度越大。理由很简单:周长越小,星体表面离中心越近,因而表面的引力越强,粒子为了逃脱星体的引力作用就越困难。
米歇尔推论,存在一个临界周长,对它来说逃逸速度是光速。如果光微粒像其他类型的粒子一样受引力作用,那么光几乎不能从具有临界周长的星体逃逸出去。对更小的星体光就完全不能逃逸了。如果以标准光速299 792千米/秒从这样的星体发射一颗光微粒,微粒起初会向上,然后慢慢停下来,又落回星体表面,见图3.1。

图3.1米歇尔1783年用牛顿引力定律和
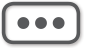
米歇尔能够很容易地计算临界周长。假如星体与太阳有相同质量,那么周长是18.5千米,而且随质量成比例地增大。
18世纪的物理学定律无法阻止如此致密星体的存在,因此,米歇尔猜想,宇宙中可能存在大量这样的黑(暗)星,它们都圆满地存在于自己的临界周长内,从地球看不到它们,因为从它表面发出的光微粒都被无情地拉回去了。这样的暗星就是黑洞在18世纪的形式。
米歇尔是英格兰约克郡桑希尔的教区长,1783年11月27日,他向皇家学会报告了也许存在暗星的预言。报告在英国自然哲学界产生了一点影响。13年后,法国自然哲学家拉普拉斯(Pierre Simon Laplace)在他的名著《宇宙体系论》的第1版里,通俗地提出了相同的预言,而没有提到比他更早的米歇尔的工作。在1799年的第2版里,拉普拉斯还保留了暗星的预言;但是到第3版(1808年)的时候,托马斯·杨(Thomas Young)发现了光的自干涉,
 证实了惠更斯(Christiann Huygens)提出的光的波动描述,从而迫使自然哲学家们放弃光的微粒描述——不过那时还不知道如何协调波动描述与牛顿引力定律,以计算星体引力对它发出的光的作用。大概为了这个原因,拉普拉斯在第3版和后来的版本中删除了暗星的概念。
证实了惠更斯(Christiann Huygens)提出的光的波动描述,从而迫使自然哲学家们放弃光的微粒描述——不过那时还不知道如何协调波动描述与牛顿引力定律,以计算星体引力对它发出的光的作用。大概为了这个原因,拉普拉斯在第3版和后来的版本中删除了暗星的概念。

只有在1915年11月,爱因斯坦建立了广义相对论的引力定律以后,物理学家才又一次相信他们对引力和光的认识已经足以计算星体引力对它发出的光的作用了。只有在这个时候,他们才又满怀信心地转到米歇尔和拉普拉斯的暗星(黑洞)上来。
第一步是史瓦西(Karl Schwarzschild)迈出的,他是20世纪初最有名的天体物理学家。那时,他正在第一次世界大战俄国前线的德国军队服役,在1915年的《普鲁士科学院会议报告》里看到了爱因斯坦建立的广义相对论。他几乎立即就开始寻找爱因斯坦的新引力定律对星体能作出什么预言。
由于分析旋转的或非球形的星体在数学上很复杂,为了简化计算,史瓦西只考虑了完全没有旋转的球状星体,他先去找星体外部的数学描述,然后再来揭示星体的内部。几天之内,他就找到了答案。他根据爱因斯坦的新场方程,详细计算了任意无旋转球状星体外的时空曲率。他的计算简洁而优美,计算所预言的弯曲几何,很快成为大家所熟悉的史瓦西几何,注定会对我们认识引力和宇宙产生巨大的影响。
史瓦西把计算论文寄给爱因斯坦。1916年1月13日,爱因斯坦代表他在柏林普鲁士科学院的一次会议上作了报告。几个星期后,爱因斯坦向科学院报告了史瓦西的第二篇论文:关于星体内部的时空弯曲的精确计算。
 仅仅4个月后,史瓦西令人瞩目的成果终止了:6月19日,爱因斯坦悲痛地向科学院报告,卡尔·史瓦西在俄国前线染病去世了。
仅仅4个月后,史瓦西令人瞩目的成果终止了:6月19日,爱因斯坦悲痛地向科学院报告,卡尔·史瓦西在俄国前线染病去世了。
史瓦西几何是我们在本书遇到的第一个时空弯曲的具体例子,而且对黑洞性质非常重要,所以我们要详细地来考察它。
假如我们把在空间和时间各处的所有活动都想象为一个绝对的统一的四维时空“结构”,那么,用弯曲(卷曲)的四维时空语言来描述史瓦西几何真是再恰当不过了。然而,我们日常经历的是三维空间与一维时间,它们是没有统一的。所以,我在描述中,将卷曲的时空分解为卷曲的空间加卷曲的时间。
因为空间和时间是“相对的”(如果我们彼此相对运动,则我的空间不同于你的空间,我的时间也不同于你的时间
 ),时空的分解首先要求选择一个参照系——也就是选择一种运动状态。对某颗星而言,我们有一种自然的选择,即令星体处于静止,也就是,我们选择星体自己的参照系。换句话说,我们来检验星体自己的空间和时间而不是某个高速经过星体的运动者的空间和时间,这是很自然的。
),时空的分解首先要求选择一个参照系——也就是选择一种运动状态。对某颗星而言,我们有一种自然的选择,即令星体处于静止,也就是,我们选择星体自己的参照系。换句话说,我们来检验星体自己的空间和时间而不是某个高速经过星体的运动者的空间和时间,这是很自然的。

身穿学者长袍的卡尔·史瓦西在德国哥廷根
[美国物理学联合会(AIP)Emilio Segrè图像档案馆提供。]
为了更形象地认识星体空间的曲率(卷曲),我将借助一种叫嵌入图的绘图方法。因为嵌入图将在以后的章节里充当重要角色,我现在通过类比来仔细介绍这个概念。
想象一族生活在只有两个空间维的宇宙中的类人生物,他们的宇宙是一个弯曲的碗面,如图3.2所示。他们也跟他们的宇宙一样,是二维的,在垂直于曲面的方向上,是无限薄的。而且,他们看不到曲面的外头,他们通过在曲面上运动而永不离开曲面的光来观察事物。于是,这些“二维生物”(我这么称呼他们)没有任何方法来获得关于他们二维宇宙以外的任何事物的任何信息。
二维生物可以通过对直线、三角形和圆的测量来探索他们二维宇宙的几何。他们的直线是第2章讨论过的“测地线”(图2.4及有关正文):他们二维宇宙中存在的最直的线。在他们宇宙的“碗”底(在图3.2中我们看到是球面的一部分),他们的直线是像地球赤道或者经线一样的大圆的一部分。在碗口以外,他们的宇宙是平坦的,所以那里的直线是我们通常所认识的直线。
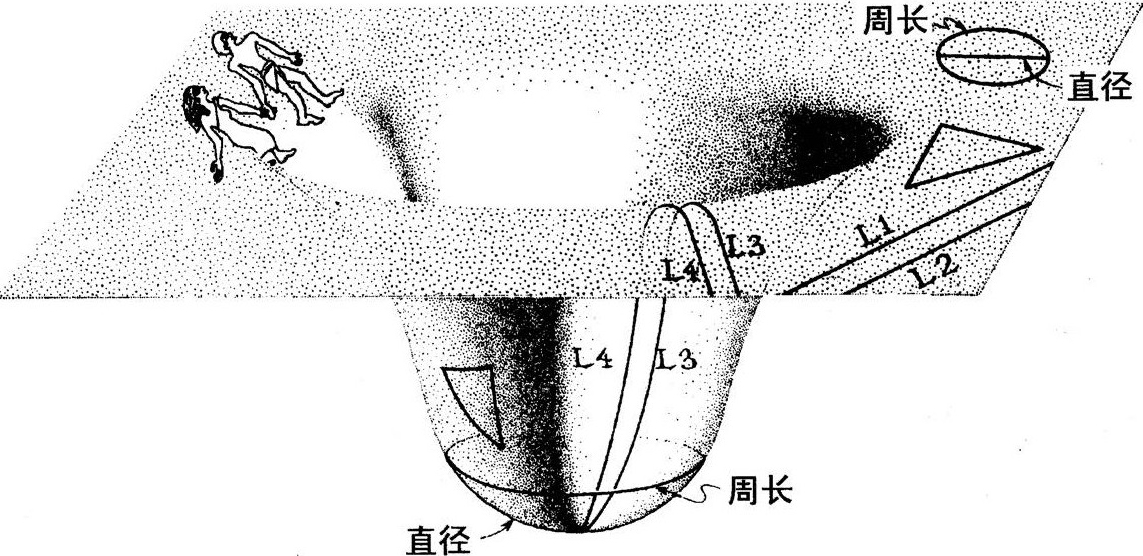
图3.2居住着二维生命的二维宇宙
如果二维生物去检验他们宇宙外部平直部分的一对平行直线(如图3.2中的L1和L2),那么不论他们跟踪直线多远,都不会看到它们相交。用这个办法,他们发现外部区域是平直的。另一方面,如果他们在碗口外作平行直线L3和L4,然后跟踪两线进入碗内,尽可能让它们保持为直线(测地线),他们将看到线在碗底相交。他们用这个办法发现,在碗的内部区域,他们的宇宙是弯曲的。
通过测量圆和三角形(图3.2),二维生物也可以发现外部区域是平直的,而内部区域是弯曲的。在外部区域,所有圆的周长都等于π(3.141 592 65…)乘以它们的直径。在内部区域,圆的周长小于π乘以圆的直径。例如,图3.2中近碗底的大圆的周长等于2.5乘以直径。如果二维生物以直线(测地线)为边作一个三角形,然后将三个内角相加,那么,在平直的外部区域,结果是180度;而在弯曲的内部区域,结果会大于180度。
通过这些测量,二维生物发现了他们的宇宙是弯曲的,接着他们开始推测,可能存在一个三维空间,他们的宇宙就处在——即嵌在其中。他们可能将那个三维空间叫超空间并猜想它的性质。例如,他们可能想象它在欧几里得意义上是“平直的”(其中的平行线永不相交)。你我看这个空间都没有困难,它就是图3.2中的三维空间,我们每天经历的空间。然而,二维生物因为只有二维经验,他们来看这个空间是大有困难的。而且,他们不可能有什么办法知道,这样的超曲面是否真的存在。他们不可能走出二维宇宙进入超曲面的第三维,又因为只能通过永远在宇宙中的光线来观察,所以他们永远也看不到超曲面。对他们来说,超曲面完全是假想的。
超曲面的第三维与二维生物可能也会认为是第三维的“时间维”无关。当他们想象超曲面时,实际不得不用四维的语言:两维是他们宇宙的空间,一维是它的时间,还有一维,就是超曲面的第三维。
我们是三维生物,生活在一个弯曲的三维空间里。如果我们也去测量我们在一个星体内部和附近的空间几何——史瓦西几何,我们将发现它会像二维生物的宇宙那样弯曲。
我们可以想象一个更高维的平直超曲面,我们弯曲的三维空间就嵌在其中。为了适应像我们这样的三维弯曲空间,结果,这样的超曲面必须有六个维。(记住,我们的宇宙也有一个时间维,所以总体上我们必须在七维下进行思考。)
现在,要我将我们嵌在六维超曲面中的三维空间形象地表现出来,就比二维生物表示他们嵌在三维超曲面中的二维宇宙,困难得多了。不过,有一种技巧可以帮很大的忙,如图3.3。
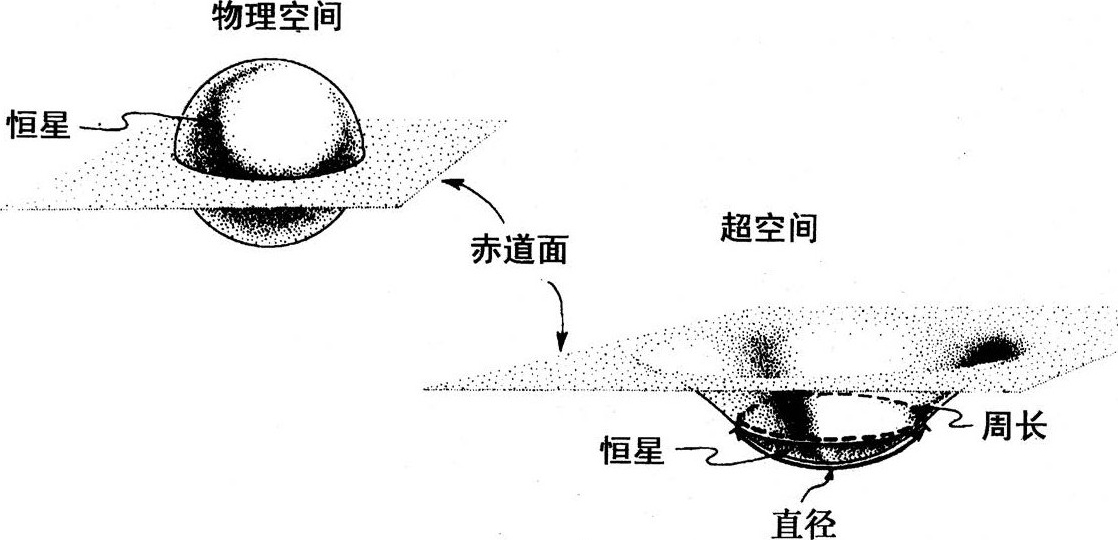
图3.3用嵌入图(右下)表示的星体内部和
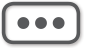
图3.3描述了一个思想实验:将一张薄片插入一个星体的赤道平面(左上图),薄片将星体切成完全相同的上下两半。赤道薄片虽然在图中看起来还是平的,但实际上是不平的。星体的质量使星体内部和周围的三维空间发生卷曲(左上图不能表现卷曲方式),卷曲又以图中没有表现的方式使赤道片发生弯曲。我们可以完全像二维生物在他们宇宙的二维空间那样,在我们真实的物理空间中进行几何测量,从而发现薄片的曲率。这样的测量将揭示,原先平行的直线在星体中心附近相交,任何星体内部或附近的圆的周长小于π乘以其直径,三角形内角和大于180度。弯曲空间的这些古怪事情都是爱因斯坦方程的史瓦西解预言的。
为了形象地表现史瓦西曲率,我们可以像二维生物那样,想象将赤道片从我们宇宙弯曲的三维空间中取出来,然后将它嵌入一个假想的平直的三维超曲面(图3.3右下)。在没有弯曲的超曲面中,薄片只有向下弯曲成碗状,才能保持它的弯曲几何。这样从我们弯曲宇宙中取出来嵌入假想的三维平直超曲面的二维薄片图,就叫嵌入图。
将超曲面的第三维想象为我们自己宇宙的第三个空间维是很诱人的,但我们必须拒绝这种诱惑。超曲面的第三维与我们自己宇宙的任何一维都没有任何关系,那一维我们既走不进也看不见,也不能从它得到任何信息,是纯假想的一维。不过,它还是有用的。它可以帮助我们看见史瓦西几何,而且在本书后面它还将帮助我们看见其他的弯曲几何:黑洞的、引力波的、奇点的和虫洞的(见第6,7,10,13和14章)。
如从图3.3的嵌入图所看到的,星体赤道片的史瓦西几何在定性上同二维生物宇宙的几何是一样的:在星体内部,几何是碗状弯曲的,在远离星体的地方,几何是平直的。跟在二维生物的碗内的大圆(图3.2)一样,在这儿(图3.3),星体的周长除以直径也小于π。对我们的太阳而言,它预言周长与直径之比比π小百万分之几。换句话说,在太阳内部,空间在百万分之几以内的精度上是平直的。然而,假如让太阳保持相同的质量而周长越来越小,那么它内部的曲率会越来越大,图3.3的嵌入图的碗的下凹将更显著,周长与直径之比将大大地小于π。
因为在不同参照系中空间的曲率不同(“如果我们彼此相对运动,你的空间是我的空间和我的时间的混合”),所以在相对于星体以高速度运动的参照系中和在星体处于静止的参照系中所测量的星体空间弯曲的细节是不同的。在高速参照系的空间里,星体在垂直于运动的方向上以某种方式被压扁了,所以嵌入图很像图3.3的,但碗被横向挤压成为长椭圆形。压扁是弯曲空间发生了菲兹杰拉德在无引力宇宙中所发现的空间收缩的结果(见第1章)。
爱因斯坦场方程的史瓦西解不仅描述了空间的曲率(或卷曲),还描述了星体附近的时间卷曲——由星体的强大引力产生的卷曲。在相对于星体静止或飞行速度不高的参照系中,时间卷曲完全是第2章讨论过的引力时间膨胀(卡片2.4及相关讨论):靠近星体表面的时间流比远处的慢,而在星体中心,时间流更慢。
在太阳的情形,时间卷曲很小:在太阳表面,时间流只比远离太阳慢百万分之二(1年慢64秒),而在太阳中心,它比在远处慢大约十万分之一(1年慢5分钟)。然而,如果太阳保持相同质量而周长更小,表面离中心更近,那么引力作用会更强。相应地,它的引力时间膨胀——时间卷曲——将变得更大。
时间卷曲的一个结果是,从恒星发出的光会经历引力红移。因为光的振荡频率由光发射处的时间流决定,从星体表面的原子发出的光在到达地球时,将比从星际空间的同类原子发出的光具有更低的频率。频率降低的量完全与时间流变慢的数量相同。较低的频率意味着较大的波长,所以,来自星体的光必然会以星体表面时间膨胀的数量向光谱的红端移动。
在太阳表面,时间膨胀为百万分之二,所以,从太阳到达地球时,光的引力红移也是百万分之二。在爱因斯坦时代,这么小的红移是不能确定地测量的。但在60年代初,实验技术赶上了爱因斯坦的引力定律:普林斯顿大学的布劳特(Jim Brault)用一个精巧的实验测量了太阳光的红移,得到了与爱因斯坦预言非常一致的结果。

在史瓦西过早去世后的几年里,他的时空几何成了物理学家和天体物理学家的标准研究工具。包括爱因斯坦在内的大多数人都在研究它,估量它的意义。所有的人都同意而且重视这样的结论,如果星体像太阳那样有很大的周长,那么它内部和周围的时空只会出现很小的弯曲,从它表面发出而在地球接收的光向红色方向的移动会更少。他们也同意,如果星体越致密,那么它的时空卷曲越大,从它表面发出的光的引力红移也越大。不过,很少有人愿意去认真考虑史瓦西几何在高致密星体情况下的那些极端预言(图3.4)。

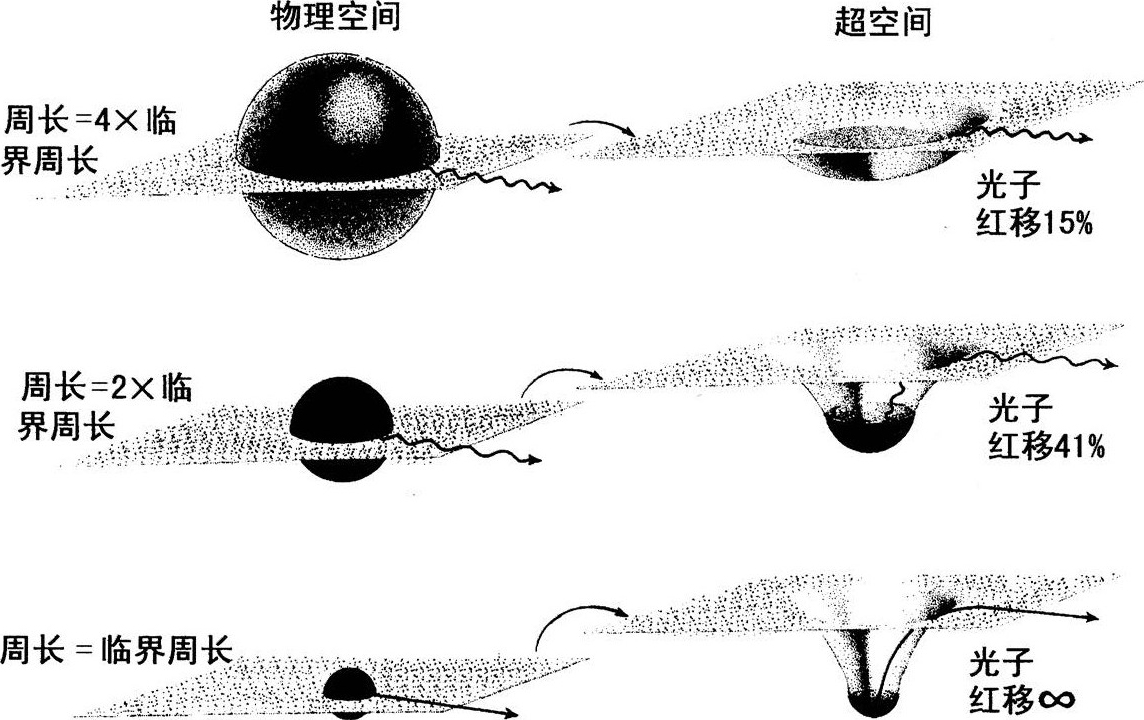
图3.4广义相对论对空间曲率和光的红移的
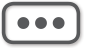
史瓦西几何预言,每个星体都存在一个依赖于星体质量的临界周长——与米歇尔和拉普拉斯在一个多世纪以前发现的那个临界周长相同:18.5千米乘以以太阳质量为单位的星体质量。如果星体的实际周长大于这个临界值的4倍(图3.4上),那么星体空间将像图中表现的那样适度弯曲,它表面的时间流会比远处的慢15%,从表面发出的光也会向红端移动15%。如果星体周长较小,只是临界值的2倍(图3.4中),它的表面将更强烈地弯曲,表面的时间会比远处的慢41%,表面发出的光也将红移41%。这些预言看来都是合理的,可以接受的。在20年代甚至60年代末的物理学家和天体物理学家们看来根本不合理的,是在实际周长与临界值相同的星体情况下的预言(图3.4下)。这样一个星体,因为它更强烈弯曲的空间,表面的时间流无限地膨胀,时间根本不流了——冻结了。相应的是,不论从星体表面出发向上旅行的光开始是什么颜色,它都一定会移过光谱的红端,超越红外线,超越无线电波的波长,一直到无限大,就是说,直到不存在。用现代语言来说,具有临界周长的星体表面正好处在黑洞的视界;而星体以它强大的引力产生一个包围它自身的黑洞视界。
史瓦西几何论证的基本观点与米歇尔和拉普拉斯发现的相同:像临界周长那么小的星体,从远处看来,必然完全是黑的,一定是我们现在所说的黑洞。尽管基本结果相同,但机制完全不同。
米歇尔和拉普拉斯基于牛顿的空间和时间绝对而光速相对的观点相信,对刚好比临界周长小一点儿的星体,光微粒几乎逃逸了。它们会飞到离星体很远的高度,比任何行星轨道还高;但当它们向上爬的时候,将被星体引力减慢,停在某个尚未达到星际空间的地方,然后调头,被拉回星体。尽管在沿轨道运动的行星上的生物可以通过减速的光看到这颗恒星(对他们来说,它不是黑的),但我们生活在遥远地球上的人却根本看不到它,星光不能到达我们。对我们来说,星体完全是黑的。
相反,史瓦西的时空曲率要求光总是以相同的普适速度传播,永远也不会变慢。(光速是绝对的,但空间和时间是相对的。)但是,如果光是从临界边界发出的,那么,当它向上经过无限小的距离时,它的波长必然产生无限大的移动。(波长移动之所以无限大,是因为时间流在视界处是无限膨胀的,而波长总是以与时间膨胀相同的量移动。)波长无限大移动的结果是消耗了所有的光能,因此光也不复存在了!这样,不论行星离临界边界多近,它上面的生物也根本看不见从星体发出的光。
我们将在第7章研究,从黑洞临界面内部看,光的行为是怎样的。我们会发现,光毕竟没有消失,它只不过是不能逃出临界面(黑洞的视界),尽管它仍在以标准的、普适的每秒299 792千米的速度向外运动。但是,本书才开头,我们还不能很好地理解这种看似矛盾的行为。现在,我们必须首先建立对其他事物的认识,这也是从1916到1960年这几十年间物理学家们所做的。
在20年代和进入30年代后,世界上最有名的广义相对论专家是爱因斯坦和英国天文学家爱丁顿(Arthur Eddington)。虽然别人也懂相对论,但爱因斯坦和爱丁顿为这个学科定下了理性的基调。在有人愿意把黑洞当真时,爱因斯坦和爱丁顿不愿意。黑洞就是“味不对”,它们太奇怪了,它们违背了爱因斯坦和爱丁顿关于我们的宇宙应该如何表现的直觉。
爱因斯坦在20年代似乎已经研究过这个问题,却将它忽略了。那时候,没人认为黑洞是什么重要的预言,所以也没有多大必要为此清理这些事情。而且因为别的自然之谜更有趣,更令人困惑,所以爱因斯坦把精力放到了别的地方。
爱丁顿在20年代的方法更天真。他像个业余演员,喜欢普及科学。只要没人把黑洞太当真,它们就是在别人面前摇摆的玩物。于是,我们看到他在1926年的《恒星的内部结构》一书中写道,没有什么可观察的星体能比临界周长的星更致密:“第一,引力的作用会大得连光也不能从它逃逸,光线会像石头落回地球那样落回恒星。第二,谱线的红移会大得连它的谱都不存在了。第三,质量会产生很大的时空度规的曲率,使空间封闭起来,将星体包在里面,而将我们留在外头(不知那是什么地方)。”第一个结论是光不能逃逸的牛顿式说法;第二个结论是半精确的相对论表达;而第三个结论就是典型的爱丁顿式的夸张了。我们从图3.4的嵌入图已经清楚地看到,当星体像临界周长那么小时,空间弯曲是很强烈的,但还不是无穷大,空间当然也不会卷起来包围星体。爱丁顿大概是知道这一点的,但他的描述很动听,在天真和幽默中把握了史瓦西时空曲率的精神。
我们将在第4章看到,在30年代,要求认真考虑黑洞的压力开始增加了。随着压力的增加,爱丁顿、爱因斯坦和其他一些“一言九鼎”的人物开始明确表示他们对这些怪物的反对。
1939年,爱因斯坦发表了一篇广义相对论的计算文章,作为一个例子,他解释了为什么黑洞不能存在。
 他的计算分析了人们也许想过可以用来制造黑洞的一类理想物体。那是一个靠引力相互吸引从而聚在一起的粒子集,很像太阳通过引力作用于它的行星而将太阳系团结在一起。爱因斯坦集合的粒子都沿圆轨道围绕一个共同的中心运动,它们的轨道形成一个球面,球面上一端的粒子靠引力吸引着另一端的粒子(图3.5左)。
他的计算分析了人们也许想过可以用来制造黑洞的一类理想物体。那是一个靠引力相互吸引从而聚在一起的粒子集,很像太阳通过引力作用于它的行星而将太阳系团结在一起。爱因斯坦集合的粒子都沿圆轨道围绕一个共同的中心运动,它们的轨道形成一个球面,球面上一端的粒子靠引力吸引着另一端的粒子(图3.5左)。
爱因斯坦想象,让集合越来越小,将实际周长向临界周长压缩。正如我们所预料的,他的计算表明,集合越紧密,球面的引力越强,在球面上运动的粒子为不至被引力拉进去,一定会运动得更快。爱因斯坦证明如果集合小于1.5倍临界周长,引力将非常强大,为避免被它吸进去,粒子不得不比光还跑得快。因为没有东西能比光运动得更快,所以粒子集不可能比1.5倍临界值还小。“至于为什么‘史瓦西奇点’不存在于物理学实体中”,爱因斯坦写道,“这个考察的基本结果说得很清楚了。”
图3.5爱因斯坦关于不可能存在像临界周长
作为对自己观点的支持,爱因斯坦还借助了一个其物质密度为常数的理想星体的内部结构(图3.5右)。这样的星体靠它内部气体的压力而避免坍缩。史瓦西曾用广义相对论导出了这种星体的完备的数学描述,他的公式表明,如果让星体越来越紧密,那么,为了反抗内部引力强度的增大,星体内部的压力也一定会越来越高。史瓦西公式表明,在星体周长压缩到9/8=1.125倍临界周长时,中心压力成为无限大。因为真实气体不可能产生真正的无限大的压力(任何其他物质也不能),所以爱因斯坦相信,这样的星体不可能像1.125倍临界周长那么小。

爱因斯坦的计算是正确的,但他对结果的解释却错了。他总结的结论,即没有物体能变得像临界周长那么小,更多地是由他反对史瓦西奇点(黑洞)的直觉决定的,而不是根据计算本身。回头来看,我们现在知道,正确的解释是:
爱因斯坦的粒子集和常密度星体不可能达到形成黑洞的致密程度,因为爱因斯坦需要内部的某种力来平衡引力的挤压:在恒星情形,他需要气体压力;在粒子集的情形,他需要粒子运动的离心力。事实上,在物体很接近它的临界周长时,确实没有什么力量能够抵抗引力的挤压,但这并不意味物体不能这么小。相反,它倒意味着,假如物体真那么小,那么,引力必然超越物体内部其他一切力量,挤压物体产生灾难性的坍缩,从而形成黑洞。爱因斯坦的计算没有包括坍缩的可能性(他所有的方程都忽略了这一点),所以失去了这个结果。
我们今天对黑洞概念太熟悉了,难免会问,“爱因斯坦那时怎么会那么笨?他怎么正好把产生黑洞的坍缩给忘了呢?”这种反应说明我们还不了解20年代和30年代几乎每一个人所具有的思想倾向。
人们那时对广义相对论的理解还很贫乏,没人认识到足够致密的物体必然会坍缩,而坍缩将产生黑洞。人们错误地将史瓦西奇点(黑洞)想象成一个在临界周长附近或内部的由某种内力支持着抗拒引力的物体;于是,爱因斯坦认为,他可以通过证明没有什么由内力支持的东西可以像临界周长那么小,来揭露黑洞的荒谬。
假如爱因斯坦猜想“史瓦西奇点”确实可能存在,那他当然也会认识到坍缩是它们形成的关键,而内力是无关紧要的。但是,他太相信它们不能存在了(它们“味道不对”,非常不对),跟那时差不多所有的同行一样,他的头脑里有一块打不破的石头,遮住了真理。
在怀特(Terence Hanbury White)的史诗小说《过去和未来的国王》里,有一个蚂蚁社会,它们有句格言,“凡不被禁止的事情都是必然的”。物理学定律和真实的宇宙并不是这样的。许多物理学定律允许的事情也是很不可能的,实际上从来没有发生过。一个简单的广为流传的例子是打碎在地板上的鸡蛋自发地重新聚集起来:鸡蛋落到地板上,碎成蛋黄和蛋清,将这个过程拍成电影。然后,将影片倒放,会看到鸡蛋又自发地重新聚在一起,飞离地板。物理学定律允许这样的重聚过程在时间长河里发生,但它从来没有实际发生过,因为太不可能了。
在20年代和30年代,甚至到了40年代和50年代,物理学家的黑洞研究都只在针对一个问题:物理学定律是否允许这种物体存在——而答案是不定的:乍看起来,黑洞似乎是可能的。然后,爱因斯坦、爱丁顿和其他一些人(错误地)论证,它们是不允许的。50年代,当这些论证最终被否定了以后,许多物理学家又来讨论,黑洞也许是物理学定律允许的,但太不可能了(像重组的鸡蛋那样),永远不会实际出现。
实际上,黑洞不像重组的蛋,在某些普通条件下它们是必然的。不过,只是到了60年代后期,当它们的必然的证据已经压倒一切时,大多数物理学家才开始认真面对黑洞。在接下来的三章里,我将叙述这些证据是如何在从30年代到60年代间积累起来的,又曾遇到过多少阻力。
黑洞在20世纪遇到的广泛而且几乎普遍的抵制,与它在米歇尔和拉普拉斯的18世纪受到的热烈欢迎,形成了鲜明的对比。阿尔伯达大学的当代物理学家伊斯雷尔(Werner Israel)深入研究了这段历史,猜测了这种差别的原因。
“我相信,[18世纪对黑洞的接受]不仅是18世纪90年代的革命热情的一个征兆,”他写道,“解释必然是,拉普拉斯的暗星[黑洞]没有给我们对物质的永恒性和稳定性的根深蒂固的信仰带来威胁。相反,20世纪的黑洞对那个信仰却是一个巨大的威胁。”

米歇尔和拉普拉斯都想象,它们的暗星是由与水或土或岩石或太阳密度大致相同(大约每立方英寸[16.39立方厘米]1克)的物质构成的。以这样的密度,星体若要成为暗星(包围在临界周长内),它的质量就必须比太阳大4亿倍,周长比地球轨道大3倍。这样受牛顿物理学定律支配的星体也许是奇异的,但确实没有威胁到我们关于自然的任何根深蒂固的信仰。如果谁想看看这颗恒星,他只需要站在邻近的一个行星上看它的光微粒:它们在各自的轨道内上升,然后很快落回恒星的表面。如果谁想要一块恒星组成物质的样本,他只需要飞到恒星的表面,取一块带回地球实验室来做研究。我不知道米歇尔、拉普拉斯和他们那个时代的其他人是不是想过这些事情,显然,如果他们想过,也没有什么理由替自然规律担心,替物质的永恒性和稳定性担心。
20世纪黑洞的临界边界(视界)提出了一个不同的挑战。视界上没有什么地方可以让我们看到任何发出的光,任何落进视界的东西都不可能再逃逸出来。它从我们宇宙消失了,它的消失又给物理学家关于质量和能量守恒的观念带来了严峻的挑战。
“黑洞的历史和大陆漂移(地球上大陆之间的相对漂移运动)的历史有着惊人的相似,”伊斯雷尔写道:“两者的证据到1916年就已经不容忽视了;但两种思想都被一种近乎无理的阻力在半路上阻挡了半个世纪。我相信,两种情况下的基本的心理学原因都是一样的。另外还有一个巧合:两个阻力都大约是在1960年开始崩溃的。当然,两个领域(天体物理学和地球物理学)都获益于战后的技术进步。但更有趣的是,正是在这个年代,苏联的氢弹和人造卫星扫荡了西方科学牢不可破和不容挑战的观念,而且也许还带来了更多的怀疑:在天地之间可能存在着比西方科学所能梦想的更多的东西。”
