偏差值是日本发明的
偏差值是日本发明的
想要了解考试和测验,大家比较在意的是“统计值”。这就是“偏差值”。这是每个学生都耳熟能详的一个词。
据说“偏差值”最早是在旧日本陆军炮兵训练中开始使用的。
而将“偏差值”应用到学习能力的评测指标上时,称为“学习能力偏差值”。这也是在日本发明的——如果平均分的偏差值为50,学生就可以知道自己的得分跟平均分有多大的差距了。
报志愿时决定志愿院校和报考院校时也会利用到“偏差值”。但“偏差值”的数值真的那么值得信赖吗?
让我们站在数学的角度来考虑吧。
 求得偏差值的方法
求得偏差值的方法
大家知道如何求得偏差值吗?想来很多人都饱受它的折磨,但是很多人对它却并不了解。那么让我们使用计算器来实际操作,导出偏差值。
有五个学生参加了数学考试,成绩为以下所列。请试着求出他们的偏差值。
<得分>
A:100分
B:80分
C:55分
D:40分
E:0分
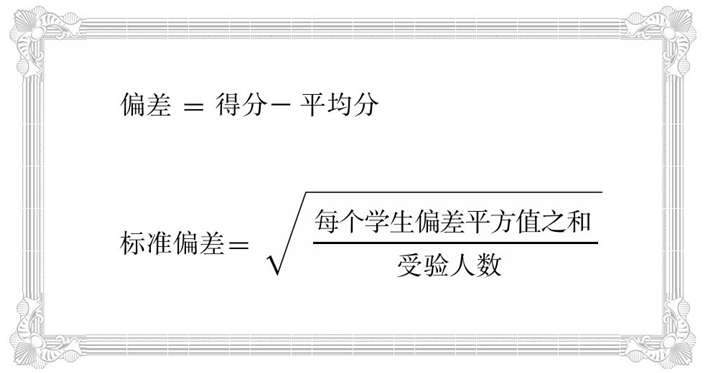
偏差值可以通过下面的公式来求得。

求偏差值的方法
偏差和标准偏差的求法
公式中的“标准偏差”的说法并不常见,它是用来表示“波动”的指标。标准偏差值很小时说明学生的得分都集中分布在平均分上下(几乎没什么波动),数值很大时得分分布得很广泛(有波动)。
将数值代入计算。
五个人的平均分可以通过他们得分的总和除以人数来求得。
五个人的平均分=(100+80+55+40+0)÷5
=275÷5
=55(分)
从平均值求得偏差,再由偏差求出标准偏差,得出34.4分。接下来用偏差和标准偏差来计算出每个学生的偏差值,得出以下结果。
<偏差值>
A:63.1
B:57.3
C:50
D:45.6
E:34.0
◆根据五个人的测试结果求出标准偏差
(A的偏差)2=(100-55)2=2025
(B的偏差)2=(80-55)2=625
(C的偏差)2=(55-55)2=0
(D的偏差)2=(40-55)2=225
(E的偏差)2=(0-55)2=3025
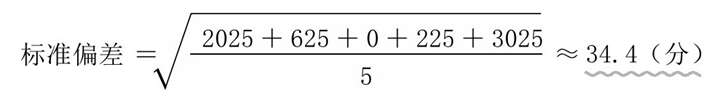
◆根据五个人的测试结果求出偏差值
A的偏差值=(100-55)/34.4×10+50≈63.1
B的偏差值=(80-55)/34.4×10+50≈57.3
C的偏差值=(55-55)/34.4×10+50=50
D的偏差值=(40-55)/34.4×10+50≈45.6
E的偏差值=(0-55)/34.4×10+50≈34.0
偏差值高于A和B为优秀,距离平均值有相当大的差距的E就要加油了,情况就是这样。
 大家要当心偏差值的圈套!
大家要当心偏差值的圈套!
在第一次考试中得了0分的E通过努力学习,在第二次考试中得到了80分的高分。
“跟上一次相比,偏差值应该有大幅提升……”E在期待中昂头挺胸地领回成绩单……没想到偏差值居然比上次还要低,真是岂有此理。E的惊讶程度可想而知。
听起来像是个玩笑,但这却是真实发生的。让我们来揭穿这个圈套吧。
分数明明比上次提高了,可是偏差值居然下降了……
<第二次考试的成绩>
A:100分
B:95分
C:95分
D:90分
E:80分
(五个人的平均分是92分)
<第二次考试的偏差值>
A:61.8分
B:54.4分
C:54.4分
D:47.1分
E:32.3分
(标准偏差是6.78分)
正态分布图
这是因为偏差值会根据平均分的不同而变化,“就算取得比0分高的分数却得到更低的偏差值”。在第二次考试中,五个人的成绩都很好,平均分高达92分。
平均分不同一眼就可以看出来,其实“偏差值的圈套”就是“得分的分布是否为正态分布”。考试结果的偏差值是否可信在很大程度上取决于这一点。
所谓正态分布,就是大多数的分数都集中在平均分上下,100分和0分都很少,画成图表就会呈左右对称的吊钟形。
参看偏差值时,重要的是“这是由几个人的集体中算出来的”。
成绩的分布一般呈正态分布。在全国几万人参加的大规模考试中,成绩的分布接近正态分布,这时得出的偏差值就比较可信。但是,只有几十人参加的考试无法形成正态分布,偏差值基本没有意义。
我们在看考试结果时,很容易被“偏差值”这项“数值”俘获,但此时我们必须了解清楚“这场考试有多少人参加”“分数是如何分布的”。
学生们不要因为偏差值而忽喜忽忧,要理解它的原理来当作前进的目标。