




尽管你记忆中对几何学的了解可能还停留在学生时代,即你对几何学的第一认知可能是:这是一门对空间进行测量
 的科学,而它所研究的问题需要考虑很多不同的距离和角度之间的数值关系(例如,著名的勾股定理,勾股定理探讨的是关于直角三角形与其三条边之间的数值关系),而实际上,许多空间中最基本的属性都不需要通过测算长度或是角度来进行研究。几何学的分支所关心的是与拓扑学或拓扑
的科学,而它所研究的问题需要考虑很多不同的距离和角度之间的数值关系(例如,著名的勾股定理,勾股定理探讨的是关于直角三角形与其三条边之间的数值关系),而实际上,许多空间中最基本的属性都不需要通过测算长度或是角度来进行研究。几何学的分支所关心的是与拓扑学或拓扑
 相关的问题,这同时也是数学中最令人兴奋却最为困难的部分之一。
相关的问题,这同时也是数学中最令人兴奋却最为困难的部分之一。
如果需要给出一个简单的拓扑问题方面的例子,我们得先设想有一个封闭的几何面,就拿一个球体的表面来说,这个球体被网状的线分割为诸多不同的区域。
通过在此球体表面定位任意数量的点,并用互不相交的线将这些点都连接起来,这样我们就可以备好一个符合要求的几何体。那么在原始点的数量、代表相邻地域间界线的数量以及区域的数量之间又存在着怎样的关系呢?
首先,我们必须非常明确的就是,若选用的不是常规的球体而是扁平的球体,比如南瓜,或是像黄瓜一样细长的几何体,那么这类球体上点的数量、线的数量以及面的数量和常规球体上的数量皆是一致的。
事实上,通过拉伸、挤压或是做任何我们想要的变形,就可随意塑造出各种闭合的表面。当然,在此过程中,唯独不能进行切割或是撕裂操作,只有这样才能保证这个几何体的构造或我们的问题的答案不发生一丝一毫的偏差。这与几何学上普通的数值关系(像线性维度、平面区域以及几何体体积之间所存在的关系)显然是相反的,形成了鲜明对比。的确,如果我们把一个立方体拉伸成一个平行六边形,或是把一个球捏成薄饼,这个关系就会发生实质上的扭曲。
用这个已划分好区域的球体,我们现在能做的就是将其每个区域都展平开来,让这个球体最终变为一个多面体(图7)。这样一来,原先连接各个不同区域的线就变作了这个多面体的棱,而最初任意选取的那些点也变为了多面体的顶点。
那么我们之前的问题(只因其考虑的关系发生了变化,而其本质和意义不发生任何改变)需要重新表述为:在一个任意类型的多面体中,其顶点数、棱数以及面数之间存在何种关系?
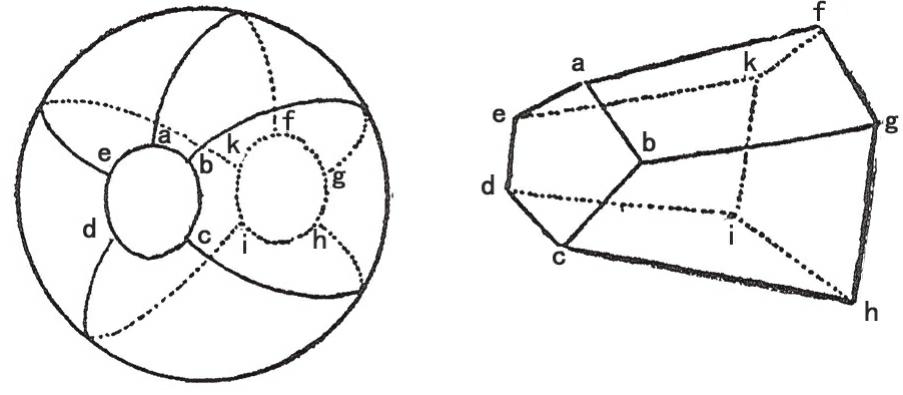
图7 一个因细分而转变成多面体的球体
在图8中,可以看见五个常规的多面体,换言之,所有这些面都拥有同等数量的棱、顶跟面,此外还附上一个仅凭想象画出来的非常规简化多面体。
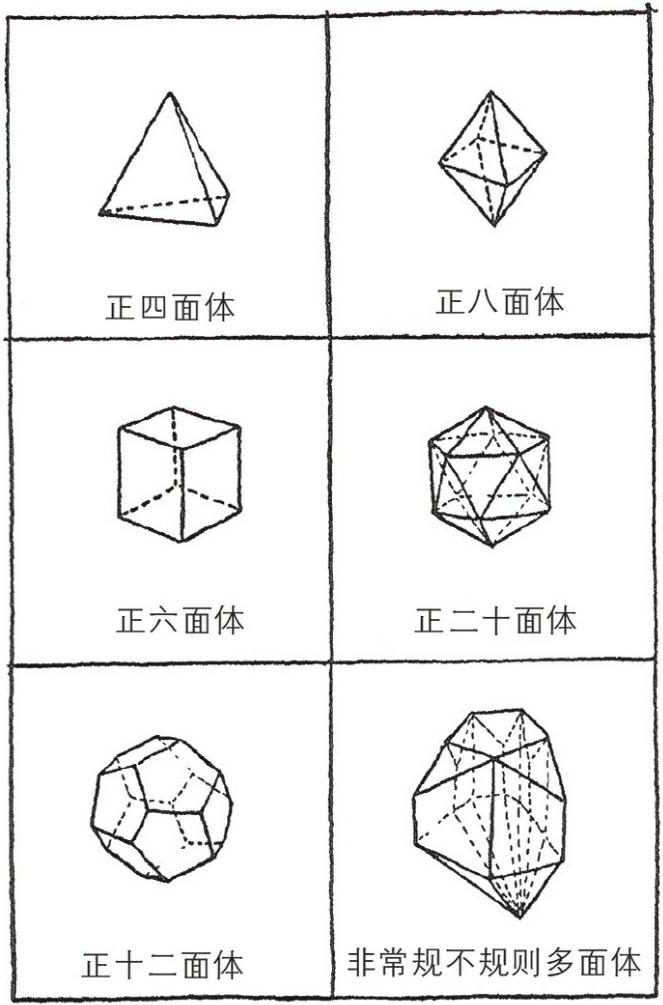
图8 五个常规多面体(只限于可能存在的
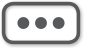
在这些几何体中,每一个我们都可以数清顶点的数量、边的数量以及面的数量。那么如果这些数值之间存在一定的关系的话,这关系会是什么?
通过直观地数算可列出以下相应的表格。
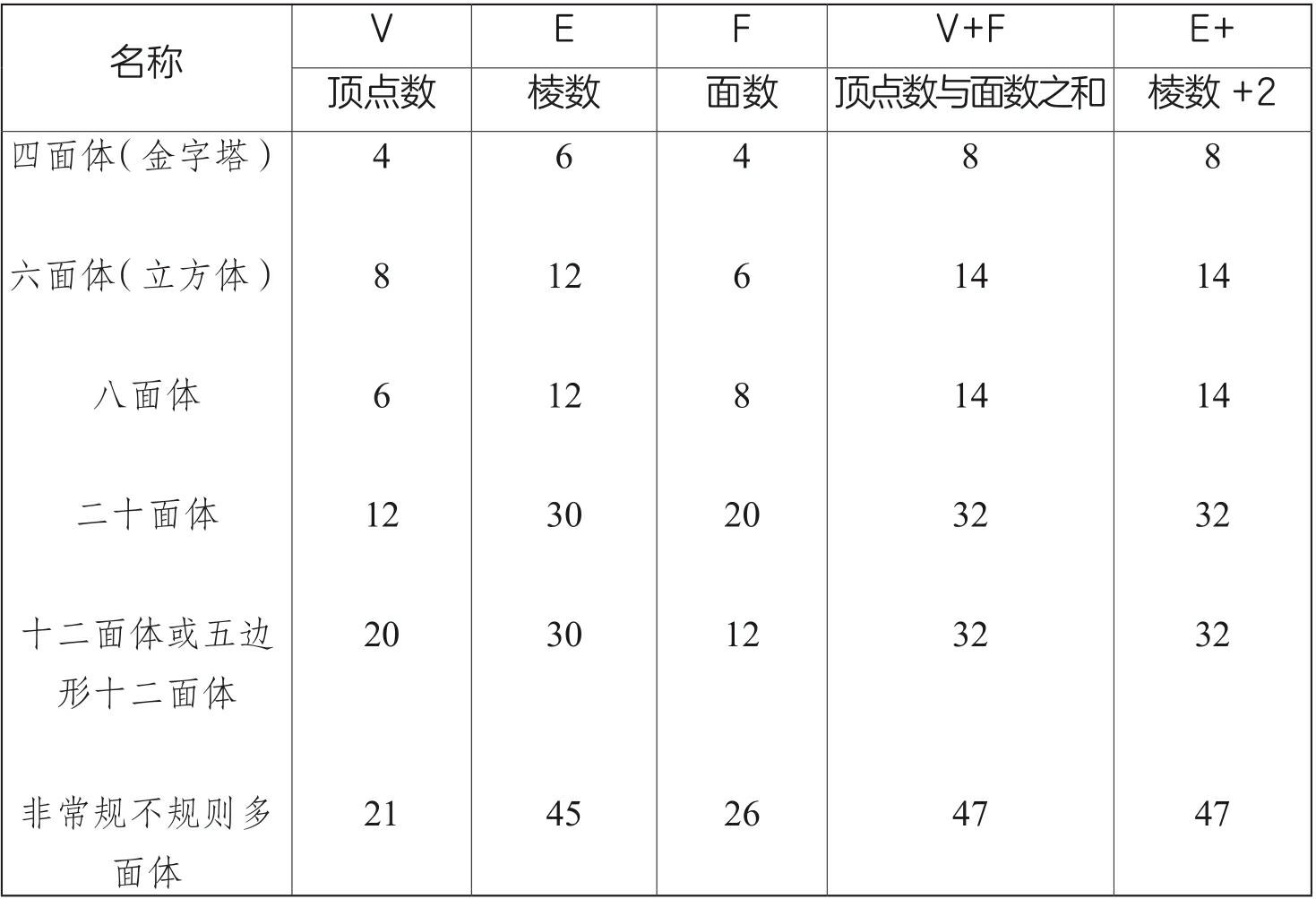
乍一看,上表前三栏所给出的数值(分别为V列、E列和F列下面的数值)之间似乎并不存在任何相关性,但仔细研究一番之后,你就会发现V栏(顶点)跟F栏(面)的数值总和总是比E栏(棱)的数值要大2。由此我们可得出如下数学关系:
V + F = E +2
那么这样的关系是否只存在于图8所列出的这五个多面体之中,抑或也同样适用于其他任何的多面体?如果你尝试着再画几个其他形状的多面体(不同于图8所列多面体),并统计一下它们的顶点数、棱数和面数,你将发现以上所得出的这种数学关系存在于每个多面体中。很显然, V + F = E +2就是一个拓扑性质的一般性数学定理,原因是其关系的表达不依赖于其棱边长度或是各个面面积的测量,而只需考虑到其中不同的几何单元(点、棱、面)的数目即可。
这样的关系只存在于一个多面体的顶点数、棱数以及面数之间,最先注意到这一关系的是17世纪法国的著名数学家勒内·笛卡儿
 。而对其进行严格证明的却是另一个数学天才莱昂哈德·欧拉(Leonhard Euler),现在这个定理正是以欧拉的名字命名的,即著名的“欧拉定理”。
。而对其进行严格证明的却是另一个数学天才莱昂哈德·欧拉(Leonhard Euler),现在这个定理正是以欧拉的名字命名的,即著名的“欧拉定理”。
现在我们一起来看一看欧拉定理(Euler's theorem)。下面是从R.柯朗
 与赫伯特·罗宾(H.Bobbins)合著的《什么是数学?》
与赫伯特·罗宾(H.Bobbins)合著的《什么是数学?》
 一书中节选出的一段原文,刚好阐明了以上所提及的欧拉定理:
一书中节选出的一段原文,刚好阐明了以上所提及的欧拉定理:
为了证明欧拉公式,我们得先设想所给定的简单多面体是空心的,且其各个面均由薄橡胶制成(图9)。那么如果切除这个空心多面体的其中一个面,我们就可以将其余的面进行形状变换,拉伸至所有面都平铺在同一平面上(图9b)。当然,在此过程中,多面体的各个面与角度之间的区域也会随着改变。但平面中的这个由顶点和棱所组成的网囊括的顶点数与棱数却是不会变的,只是多面体数会比之前少一个,这是因为在变形的过程中有一个面被移除了。这样一来,我们应该就能看出,对于平面网来说,
V
-
E
+
F
=1
 ,而对于原来的多面体来说,如果把移除的面也算在内,结果就会是
V
-
E
+
F
=2
,而对于原来的多面体来说,如果把移除的面也算在内,结果就会是
V
-
E
+
F
=2
 。
。
首先我们需要按如下方式将网状平面“进行三角形化”,也就是在此网状平面中,为形状不是三角形的多边形添加对角线(以形成三角形)。结果就是: E (棱)和 F (面)两者都增加了1,这样一来就保证了 V - E + F 的值恒定不变。现在我们继续添加对角线,将成对的点都连起来,直到此多边形完全变为内含三角形的图形为止,这才是我们最终要的效果(图9c)。在进行三角形化的网状图中, V - E + F 的值跟还未进行三角划分前的值一样,原因是进行对角线划分并不会改变这个数值。
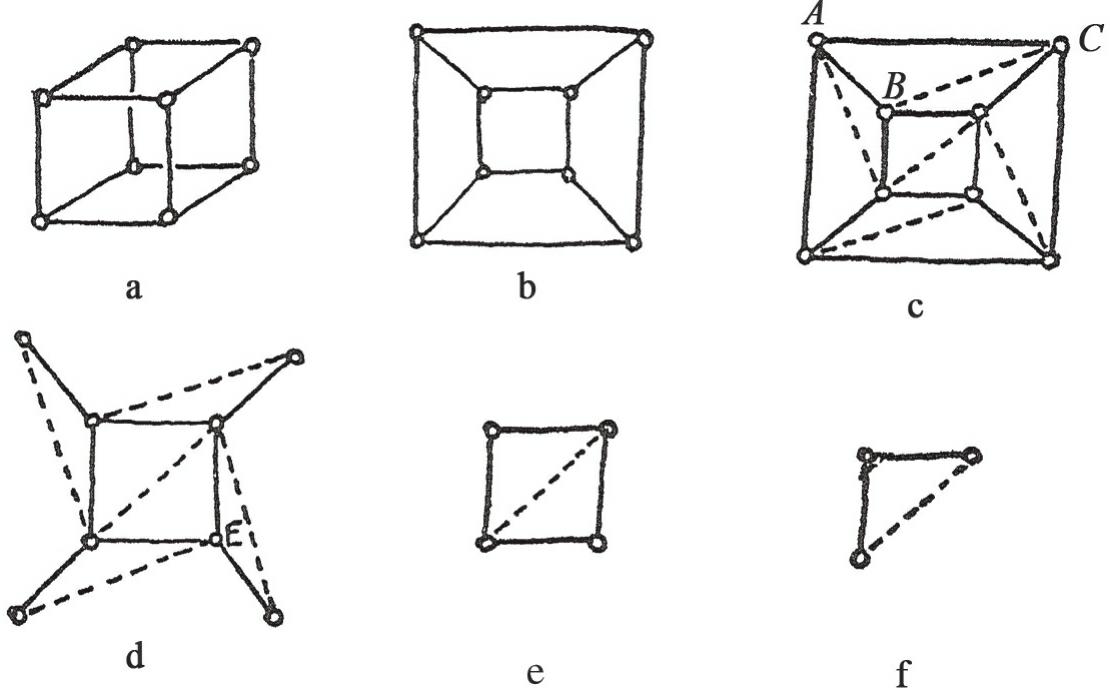
图9 欧拉定理证据。图中展示的是立方体的情况,但这不妨
有些三角形的边分布在网的边线上,与之重合。当然,还有些像三角形 ABC 这样的,只有一边位于边线上,以边线为三角形的其中一边,而另外一些三角形则可能有两条边与网的边线重合。我们取任意一个边线三角形,并去掉其中不属于其他三角形的部分(图9d)。这样在三角形 ABC 中,我们就移除了 AC 这条边以及这个面,而留下了顶点 A 、 B 、 C 以及 AB 和 BC 两条边;从三角形 DEF 中,我们需要移除三角形 DEF 这个面,以及 DF 、 FE 两条边和顶点 F 。
在对 ABC 这类三角形的移除过程中, E 跟 F 都减少了1,而 V (顶点数)则不受影响,由此得出 V - E + F 的值不变。在 DEF 这类三角形的移除过程中, V 减少了1, E 减少了2, F 减少了1,由此得出 V - E + F 的值再次保持不变。以适当的方式进行此类操作,我们可渐次移除边线三角(边线会随着每次移除发生改变),一直到最后只剩下一个三角形为止,亦即最终只剩下三条边、三个顶点和一个面(的三角形)。对于这个简单的网来说, V - E + F =3-3+1=1。但我们已经知道, V - E + F 不会随着三角形的减少而发生改变。因而在最初的平面网中, V - E + F 也必须是等于1的,且这样一来,对于少了一个面的多面体来说,这样的相等关系也还是存在的。我们于是得出如下结论: V - E + F =2适用于完整无缺的多面体。这样就完全支撑了欧拉公式。
欧拉公式中存在一项有趣的求证,即只可能存在五个常规多面体,也就是图8所示的各个多面体。
仔细回顾前几页所述的内容,你可能会注意到在画图8所示的各种多面体以及寻找证据以支撑欧拉定理的过程中,我们先做了一个隐含假设,结果导致我们的选择受到了很大的限制。也就是说,一直以来,我们习惯于将自己局限于多面体,不会有任何的洞透过其间。我们这里所说的洞,并不是那种橡胶气球上撕去一块而产生的洞,而是指甜甜圈或闭合的橡胶轮胎中间(凹陷)的空洞。
让我们来看一下图10,图10将会为您澄清这个情况。在图中我们可以看见两个不同的几何体,其中任何一个都与图8中所展示的几何体一样,都是多面体。
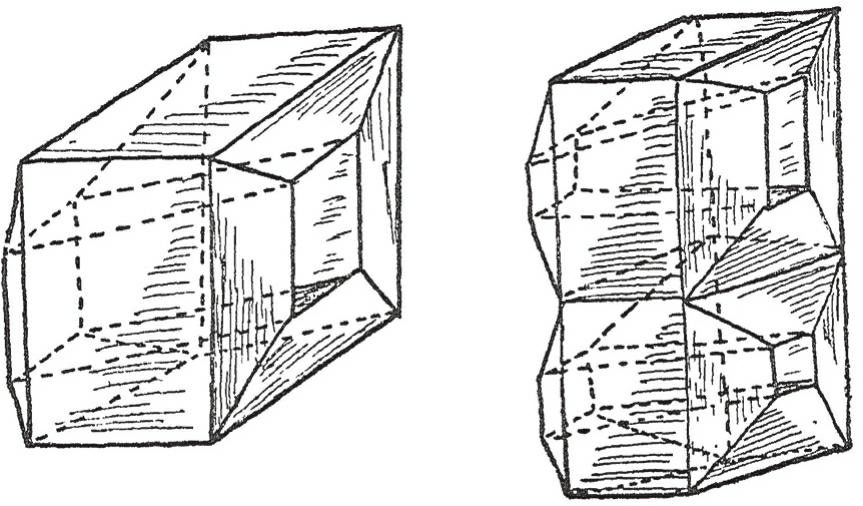
图10 这两个普通的立方体分别只有一个和两个洞自其中透
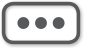
现在让我们来看看欧拉定理是否适用于这两个新的多面体。
在所给出的第一个案例中,(经计算)一共有16个顶点、32条棱以及16个面。这样的话, V + F =32,而 E +2=34。在第二个案例中,通过计算我们得知这个多面体共有28个顶点、60条棱和30个面,那么相应地, V + F =58,而 E +2=62。这又不对了!
那么为什么会这样呢?在上面所给出的例子中,为什么我们按欧拉定理给出的一般依据会不适用呢?问题到底出在哪里?
当然,问题就在于我们一直以来所研究的多面体可以看成一个球胆或气球,而这种新型的中空式多面体却更像是一个轮胎内胎或是橡胶制品中构造更为复杂的某种成品。
对于后面提到的这类多面体,以上所给出的数学证明就不适用了,原因是,对这种类型的几何体我们无法进行证明所需的所有步骤。所以,在实际生活中,遇到此类情况我们会被要求:“切除中空多面体的其中一个面,还要将余下的面都拉伸变形直至平摊到同一个平面上。”
如果你用剪刀剪去足球表面的一部分,你同样可以满足这个证明步骤。但如果你选用的是一个轮胎内胎的话,那么不管你多努力地做出尝试,你都不可能满足上述证明步骤。要是观察图10还不能让你完全信服这一点的话,你倒是可以换一个旧轮胎亲自试试!
但是,一定不要想当然地认为对于较复杂的多面体来说, V 、 E 和 F 之间就不存在任何关系了,关系肯定是存在的,只是有别于之前的关系罢了。而对于甜甜圈状的,抑或更科学严谨一点说,对于环形曲面状的多面体而言,计算公式 V + F = E 派得上用场。而对于椒盐卷饼状的多面体,我们又需要 V + F = E -2这样的公式。一般而言,在 V + F = E +2-2 N 中, N 表示的是透洞的数量。
另一类与欧拉定理密切相关的典型拓扑式问题是所谓的“四色问题”。
假设我们现在有一个表面被细分为数个区域的球,且需要给这些区域都标注上特定的颜色,还要求任意两个相邻的区域(那些共享一条边界的区域)的颜色不尽相同。那么,面对这样一项任务,我们将使用到的色调中,用量最少的会是什么颜色?很显然,当三条边界都归于一点(举个例子,观察标注在同一张地图的以下地点:图11中美国的弗吉尼亚州、西弗吉尼亚州和马里兰州)时,一般而言,两种颜色是不够用的,要为三个区域上色,必须用到三种不同的颜色。
而要找一个同时含有四种颜色的地图(这是德国吞并奥地利期间瑞士的地图标志)也不难(图11)
 。
。
图11 美国弗吉尼亚州、马里兰州、西弗吉尼亚州法国、德
不管你怎么尝试,你都绝不可能靠想象构建一张需要四种以上色调上色的地图,不论这地图是放在地球仪上来看还是放平在纸张
 上来使用。看起来,人制地图的时候不管多复杂,四种颜色也总是够用了,也足以避免边界混淆的情况发生了。
上来使用。看起来,人制地图的时候不管多复杂,四种颜色也总是够用了,也足以避免边界混淆的情况发生了。
如果最后的这个陈述是真的,那它一定能经由数学证明有效。但不论经过了多少代数学家的努力,最终的证明都没能给出。这属于那种实际生活中无人怀疑,但数学上却无人能证明的典型数学案例。现在,我们最多能成功地经由数学证明有五种颜色就足以应付所有会出现的情况。这个证明是基于对欧拉定理的实际应用做出的,证明的过程中考虑到了国家的数量、相应国家边界的数量,以及几个国家聚在一起时三倍、四倍等数量的交点。
我们不再演示这个证明过程,因为此过程实在太过繁杂难懂,很有可能将我们带离正在讨论的主题,读者自己(要是感兴趣的话)可从几本不同的拓扑学著作中找到相应的内容,并在其陪伴下度过一个愉快的夜晚(也可能是不眠之夜哦),以沉思个中奥秘。
要是有人能找出证据证明在给任何一张地图着色的时候,不需要五种颜色,其实四种就已经够用了;或者,要是有人对以上言论表示怀疑并设计出一张四种色调不够用的地图来,那么,以上两件事,只要有人做成了其中一件,那个人的大名就将于今后几世纪永载纯数学的史册。
但具讽刺意味的是,愈加复杂的表面,例如,甜甜圈或是椒盐卷饼的表面,都能被相对轻松地证明出来,而对于常规的球体或是平面,数学家却只能望洋兴叹、绕道而行,从未成功证明出来过。据可靠的例子表明,不管甜甜圈怎样划分和组合,七种颜色足以满足所有的需求,且能保证相邻的两个部分之间所上色调不尽相同。这还有相应的实例给予支持。
读者要是想再花些心思,弄到一个充气轮胎的内胎和一套七色的油彩,来给内胎表面上色,他得保证所涂的每一种颜色跟其他六种颜色相邻才行。完成这些之后,他就可以说:“我现在真的知道炸面包圈的方法啦
 。”
。”