




我们都知道空间是什么,但一旦被问及“空间”这个词所指的准确定义时,我们还是会尴尬地发现自己竟很难说出个所以然来。这时候我们的措辞很可能会是:空间就是环绕着、包裹着我们的所在,且通过它,我们可以在其中进行前后、左右乃至上下的移动。这个由三个相互独立且垂直的方位所组成的存在体,它代表的是我们居住的这个物理空间所具有的最基本的其中的一个属性;这就是我们会称我们所在的空间为三向抑或三维空间的原因。空间里的任何一个位置都可由这三个方向明确地定位出来。若我们现在正身处一座陌生的城市,并向酒店前台询问如何才能找到某个知名公司的办事处,这时候工作人员的回答可能是:“(您需要先)向南面步行五个街区,接着右转经过两个街区,最后再往上爬七层楼。”刚刚这个例子里所给出的三个数通常被认作是坐标(的组成要素),其中涉及了街区与建筑物楼层以及酒店大堂这个原始出发点之间的联系。而很明显的是,通过使用坐标系,同一个地点的方位可由另外的任何一个点指出,这个坐标系将准确地表明新的始发点与终点之间的联系。而只要我们知道新坐标之于已有坐标的相对位置,那么经由简单的数学演算,新坐标就可以通过已有坐标表达出来。这个过程就是所谓的坐标变换。这里可能需做出的补充是,所有的这三个坐标都不需要使用代表一定距离的数字来表示,而实际上,在某些特定的情况下,使用角坐标则会更便利一些。
举例而言,在纽约,街区和道路间相交形成了直角坐标系,那么这就是其最为自然而合理的地址表达方式;而莫斯科(俄罗斯)的地址体系则必然要通过变换为极坐标才能获得。长久以来,这座古老的城市就是围绕着中央要塞—克里姆林宫发展起来的,故以克里姆林宫为中心,街道向四周呈放射状发展,而与之纵横交错的是几条同心的环形林荫道,所以要是有人描述有一栋房子是位于克里姆林宫宫墙西北偏北方向二十个街区的位置上,这样的说法倒也合乎情理。
另一个关于直角坐标系和极坐标系的经典例子是美国海军部大楼以及华盛顿特区陆军部大楼,因其与“二战”期间的战争部署工作紧密相关,故(只要提到)每个人都很熟悉。
在图6所给出的样例中,经由三个或表示距离或表示角度的坐标,我们展示了如何通过不同的方式来描述一个点在空间中的位置。但不论我们所选用的是何种体系,都需要三个数据来进行定位,因为我们试图解决的是三维空间内的问题。
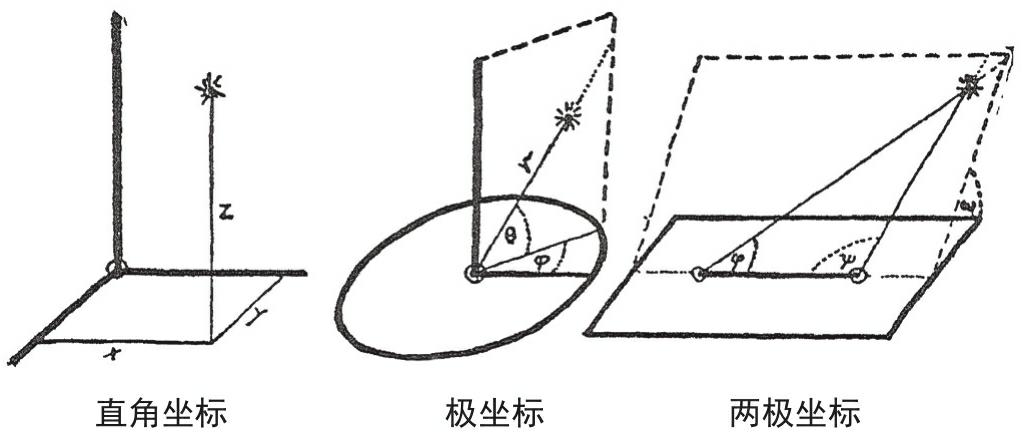
图6 三个坐标表示空间中一点的所在位置
虽然对我们来说,使用根深蒂固的三维空间概念去想象超空间,即所拥有的维度多于三维的多维空间(然而,正如我们稍后将会看到的,这样的空间确实存在)是一件很不容易的事情,但其实我们很容易就能在脑海中构架出一个少于三维的子空间。一个平面、一个球体的表面,或者其他任何物体的表面,其实都是一个二维空间,因为表面上的一个点,其位置总能由唯一的两个数字表示出来。同样,(或直或曲的)一条线是一个一维度的子空间,且只需一个数字用于标示其所在位置。我们也可以说一个点就是一个零维度的子空间,原因是在一个点内不存在两个不同的位置。但谁又会对点产生兴趣呢!
作为三维生物,我们会发现要理解线段跟平面的几何属性会更简单一些,因为我们可以“由内而外”看见其全貌,而对于我们更为熟悉的三维空间属性,正因我们身处其中
 ,则更难窥其全貌,也就更难理解(三维的概念所指)。这就解释了为何你能毫无困难地理解什么是曲线或什么是曲面,却会被三维空间也可以弯曲这种说法吓到。
,则更难窥其全貌,也就更难理解(三维的概念所指)。这就解释了为何你能毫无困难地理解什么是曲线或什么是曲面,却会被三维空间也可以弯曲这种说法吓到。
然而,只要通过一点练习来了解“弯曲率”这个词的真正含义,你就会发现一个弯曲的三维空间这样的概念的确非常简单,而在下一章的末尾部分,你将会(我们希望!)甚至是很放松地对一个乍一看似乎很可怕的概念—(将要提到的)弯曲的四维空间畅所欲言。
但在我们进行更进一步的讨论之前,让我们先来尝试接触一些有关普通三维空间、二维平面及一维线条的智力训练吧。