





数据分组是统计研究中非常重要的一环,分组的效果高度影响着总体特征的统计。如果数据分组不够科学,那么频数统计及其他研究也就失去了意义。然而,数据分组却是一个比较复杂的过程。
数据分组就是根据统计研究的任务,按照一定的标志,把我们所研究的社会现象总体区分为若干性质相同的组。简言之,数据分组就是把总体中性质相同的单位归并在一起,把性质不同的单位区分开来。其作用是区分现象的不同类型,研究总体的内部结构,分析现象间的依存关系。
例如,要了解我国人口状况,只知道总人口数量是不够的,而应将人口总体按照年龄、性别、民族、城乡、文化程度等分组,才能进一步深入地了解我国人口总体的年龄结构、性别比例、民族构成等。
数据分组是整个统计工作中常用的一种重要方法,在数据整理中,在统计数据研究中都要广泛应用分组。分组方法得当,对大量统计数字资料进行科学的整理和深入的分析,才能对一系列经济理论问题做出科学的判断。而分组方法不当,同一材料甚至可能得出完全相反的结论,可见,数据分组十分重要。分组的好坏直接关系到统计能否整理出正确的、中肯的统计信息,关系统计能否得出正确的结论。
1.数据分组的含义
从分组的性质来看,分组兼有分和合的双重性含义:
(1)对于现象总体而言,是“分”,即把总体分为性质相异的若干部分;对于单位而言,又是“合”,即把性质相同的许多单位结合为一组。
(2)对于分组标志而言,是“分”,即按分组标志将不同的标志表现分为若干组;而对于其他标志而言,是“合”,即在一个组内的各单位即使其他标志表现不相同也只能结合在一组。
由此可见,选择一种分组方法,突出了一种差异,显示了一种矛盾,必然同时掩盖了其他差异,忽略了其他矛盾。统计研究的任何一个社会现象总体都是由许多个体单位组成的,从总体现象的任一特征观察,这些个体单位之间既有共性,又有个性即个体单位之间的差别。如大学生总体,从爱好看就有文学、艺术、音乐、体育之分;从学习成绩看就有优秀、良好、及格、不及格之分;从性格看就有活泼、内向之分,等等。这就是说,为了研究现象总体的状况,就必须对总体进行各种分组,并从数量方面深入了解和研究总体的特征。
数据分组实际上是在总体内部进行的一种定性分类,分类的结果在各组之间自然就出现了显著的差异,无论是量的差异或质的差异,都能在一定程度上反映出不同的情况。如果没有显著的差异存在,分类就没有意义,因而也就没有必要。
2.数据分组的原则
科学的数据分组应遵循以下三项原则:
(1)同异原则。
必须坚持组内数据的同质性和组间数据的异质性,这是数据分组的一个基本原则。
(2)穷尽原则。
必须符合完备性原则,即所谓“穷举”性,所有数据都必须分到某一个组当中。
(3)互斥原则。
必须遵守“互斥性”原则,即任一单位都只能归属于一组,而不能同时属于两个或两个以上的组。
只有满足以上三项原则的分组才可能是科学的数据分组,即使只有一项原则不满足,也一定不是科学的数据分组。
3.数据分组的种类
分类标准不同,数据分组的种类也不同,主要有以下几种。
(1)按分组标志的多少,可分为简单分组和复合分组。将社会经济总体只选择一个标志分组称为简单分组。复合分组是用两个或两个以上分组标志重叠起来对总体进行的分组。例如,将人口先按“性别”分成男、女两组,然后在男性和女性两组中再分别按照“文化程度”划分为大学生及大学以上、高中、初中、文盲及半文盲五组。
(2)按分组标志的性质不同,分为品质分组(或称属性分组)和数量分组(或称变量分组)。品质分组就是按品质标志进行分组。一般来说,对于以定类尺度或定序尺度计量的,采用品质分组。数量分组就是按数量标志进行分组。
(3)按分组的作用和任务不同,可分为类型分组、结构分组和分析分组。把复杂的现象总体划分为若干个不同性质的部分,就是类型分组。在对总体分组的基础上计算出各组对总体的比重以研究总体各部分的结构,就是结构分组。为研究对象之间的依存关系而进行的数据分组即分析分组。
4.数据分组的方法
数据分组的基本方法有以下两种。
(1)按品质标志分组。
按照品质标志分组又称分类,这种方法比较简单,就是用反映事物的性质的标志作为分组标志,可以将总体单位划分为若干性质不同的组成部分。例如,人口按性别、文化程度、民族、籍贯等标志分组;企业按经济类型、轻重工业、隶属关系、企业规模等标志分组等。
(2)按数量标志分组。
按数量标志分组就是按变量的取值分组,要根据变量的性质是离散型或连续型来确定,这种方法比较复杂,但它却是统计研究中的重要内容。例如,地区经济按国内生产总值分组、企业按销售收入分组等。
5.数据分组的关键
数据分组的关键问题是:正确选择分组标志和合理确定分组界限。前者主要是指品质标志分组,后者主要是指数量标志分组。前者可根据统计研究问题的具体目的要求来选取,后者则情况较复杂。
对变量数列来讲,我们见到最多的是连续型变量,即两个变量值之间的取值是无限的,如工资、产值、学生的考试成绩、人口年龄、商品价格等。而变量值的分布又具有规则的、不规则的特征,面对复杂多样的统计数据,如何正确选择分组标志和合理确定分组界限是数据分组的关键。
分组标志是将具有同一性质的数据划归为一类,将不同性质的数据列入不同组的依据。因此,选择分组标志时,一定要突出各个个体在该标志下的性质差异,而其他方面的差异可以相对忽略。选择不同的分组标志,就会产生不同的分组结果,而不同的分组结果可能会产生不同的结论。所以,选择适当的分组标志也是数据分组的核心问题。
一般来说,数据分组标志的选择应当参考以下几个原则。
1.目的性
通过数据分组来表示数据的特点,其关键性问题就是要选择合适的分组标志,只有合适的分组标志才能科学地体现总体的分类特点。在总体的各个性质中,要选择最贴近统计研究目的的性质作为分类标志,才能实现科学的分组,进而得到准确的信息,否则会造成分组的科学意义缺失、研究价值降低以及科学性缺乏等弊端。
例如,已知各行业的从业人数、总产值、行业利润率、行业企业数量这四项数据,为了研究各行业的盈利能力,要对各行业的数据进行分组,最核心的问题就是选择合适的分组标志。在这里,可选的标志有“从业人数”、“总产值”、“行业利润率”、“行业企业数量”四个。考虑到我们的研究目的是分析各行业的盈利能力,而“行业利润率”是行业利润与行业资本的比值,是行业盈利水平的衡量指标;而“从业人数”、“总产值”、“行业企业数量”则是衡量行业规模的主要指标,与行业盈利能力并无直接明显的关联,选择它们中任何一个都不能分析各行业的盈利水平。综上所述,最贴近研究目的的标志是“行业利润率”,其他标志与行业盈利能力的关联不大,因此应选择“行业利润率”作为数据分组标志。
2.本质性
分组标志的选择应当能够反映事物或现象的本质特征。明确了统计研究的目的之后,可能还会遇到有多个标志可供选择的情况,此时判断和筛选这些可选标志中的本质含义就成了主要任务。在有效标志的筛选过程中,寻找到最能反映事物本质特征的标志,就可以实现科学的统计研究。
例如,已知各国的“GDP”和“人均GDP”数据,为了研究各国的富裕程度,欲将各国的数据进行分组。“GDP”和“人均GDP”都是一国经济发展水平和国民收入的相关指标,如果按照目的性原则都可以成为分组标志,但是两者的本质含义有所不同。“GDP”是对一国经济总量的衡量,而“人均GDP”是一国国民的平均产值,代表了一国国民的实际收入水平,即富裕程度。因此,“人均GDP”的本质才是各国富裕程度的代表。综上所述,应当选择“人均GDP”作为分组的标志。
3.时效性
值得注意的是,任何事物或现象都随着时间、地点的变化而变化,要准确把握事物的性质,进行科学的统计分析,就要对其分组标志进行及时更新,保证其时效性。时效性原则上保证了各数据之间可比的关系,进而规范了数据分组的逻辑和过程,是最基本的原则之一。
例如,研究分析我国各省的外商直接投资情况,就要求分组标志能够及时更新,保证其时效性。但是统计四川省的外商直接投资数据时会遇到这样的问题:1996年及1996年以前重庆市的数据是计算在四川省内的,而1997年及1997年以后重庆市的数据是单独统计的,很明显,这样的指标就不能选为分组的标志。
根据分组标志的不同性质,统计总体可以按品质标志进行分组,也可以按数量标志进行分组。按品质分组是按品质标志进行的分组,而按变量分组是按数量标志进行的分组,例如工厂规模分组可以按职工人数、生产能力等数量标志分组。而按照数量变量分组关键的问题就是分组界限的确定。
数量标志分组,其变量有离散型变量和连续型变量两种,前者指所描述对象的数量特征可以按一定次序一一列举它的数值;后者指所描述的数量特征在一个区间里可以有无限个数值,无法一一列举。两种不同的变量类型对应不同的分组界限。在介绍分组界限的确定之前,必须理解以下两个概念。
概念一:单项式分组
单项式分组是用一个变量值或分组标志值作为一个组的代表性质,每个变量或标志值对应一个分组,当总体数据是离散型变量且变量变动范围不大时,可以选择单项式分组的分组方法,同时,单项式分组的分组方法也是按品质标志分组的主要方法。
概念二:组距式分组
组距式分组是将变量按照一定的数量或质量关系划分为几个区间段,一个区间段就是某两个变量分类界限的距离,并把一个区间段的所有变量值归为一类到一组中,形成组距式变量数列,这段区间的距离就是组距。对于连续型变量或者变动范围较大的离散型变量,适宜采用组距式分组的方法。该方法也是数量标志分组的对应分组方法。
不同的数据将面临不同的分组界限,但归纳起来,主要有以下两种形式。
1.离散型分组界限
对于离散型数据的分组,如果数据变动幅度较小,分组可以是单项式的,即将每个性质的数据分别分为一组;如果数据变动幅度较大,分组应该用组距式分组,即合并某些性质相似的数据。
例如,欲研究某高校某专业本科学生毕业年龄,就要对年龄数据进行分组。显然,某专业的本科毕业生年龄为离散型数据,而且一般来讲多为20~24岁,变化幅度较小。此时,分组应当是单项式的,应当将每个性质的数据分别分为一组,即分为20岁、21岁、22岁、23岁、24岁这五组数据,而每个年龄值就成为此例中离散型数据分组的界限。
再如,欲研究该高校某专业教师现在的年龄,同样要对年龄数据进行分组。显然,该专业的教师年龄为离散型数据,而且从30~60岁均有,变化幅度很大。此时,分组就应当是组距式的,将某些相似性质的数据合并起来。具体来讲,30~60岁基本分为30~40、40~50、50~60这3个年龄挡,分别为青年、中年、老年三个阶段的教师,因此,30、40、50这3个数字就成了离散型数据的分组界限。
下面我们通过一个实验来介绍利用Excel 2013确定离散型分组界限的方法和步骤。
实验4-1:根据西部10省区2003年的旅行社数量(单位是个),对数据进行分组。图4-1所示是原始数据。
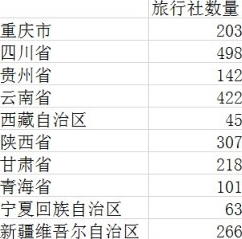
图4-1 实验4-1的原始数据
思考和操作过程如下:
(1)显然,此例中的旅行社数量是离散型的,最小的有45,最大的有498,相差十倍有余,足见变化幅度之大,所以应当将性质相似的数据分为同组,性质悬殊的分为不同的数组。我们还可以粗略地观察到,0~100,100~200,200~300,300~400这四个区间内,数据出现的次数相差不大,所以可以用这四个区间来对西部10省区进行分组。
(2)在单元格B14中输入“=COUNTIF(B2:B11,"<=100")”,按下Enter 键,得到旅行社数量在100以内的省区数。
(3)计算旅行社数量在100~200区间内的省区个数,在单元格B15中输入公式“=COUNTIF(B2:B11,"<=200")-COUNTIF(B2:B11,"<=100")”,按下Enter键,得到100~200区间内的数据个数。
(4)同理,在单元格B16和B17中依次输入公式“=COUNTIF(B2:B11,"<=300")-COUNTIF(B2:B11,"<=200")”和“=COUNTIF(B2:B11,"<=400")- COUNTIF(B2:B11,"<=300")”,按下Enter键,分别得到旅行社数量在200~300区间和300~400区间内的省区个数,结果如图4-2所示。

图4-2 实验4-1的分组结果
综上所述,分组结果比较均匀,离散型分组界限便最终确定。
2.连续型分组界限
由于连续型数据无法全部列举其数值,其分组只能是组距式分组。值得注意的是,按数量标志分组时,各个分组的数量界限的选择必须能反映各个样本的本质差异,还应根据被研究的事物或现象总体的数量特征采用适当的分组数,确定合适的组距。
例如,欲研究各个城市的海拔分布,就要对各个城市的海拔数据进行分组。很明显,各个城市的海拔是连续型的数据,对于这种数据分组必须采用组距式分组。而各个城市海拔有-40 m、10 m、2 000 m等不同数据,面对变化幅度如此之大的数据,如何选择分组界限成为最重要的问题。然而,研究城市海拔就要具备一定的地理常识,在地理学上,海拔0 m为海平面,海平面以下即海拔为负值的地区称做盆地,海拔高于0 m低于1 000 m的地区则称做平原,海拔高于1 000 m的地区称做高原,按照这种地理学常识来对各个城市的海拔数据进行分组,是最能反映数据本质特征的指标,而0 m、1 000 m则是该连续型数据分组的科学界限。
下面我们通过一个实验来介绍利用Excel 2013确定连续型分组界限的方法和步骤。
实验4-2:根据2007年全国主要城市的年降水量(单位是mm),对数据进行分组。图4-3所示是原始数据。
思考和操作过程如下:
(1)显然,此例中的降水量是连续型的,最小的有214.7,最大的有1 439.2,足见变化幅度之大,如何确定分组界限成为分组效果好坏的关键。这里研究降水量就要具备一定的地理常识,一般而言,年降水量在800 mm以上为湿润地区,年降水量在400~800 mm之间为半湿润地区,年降水量在200~400 mm之间为半干旱地区,200 mm以下为干旱地区。所以依据这个常识,我们就可以对这些降雨量数据进行分类。由于本例中的城市降水量最低值也在200 mm以上,因此这里可以分为200~400,400~800,800以上这三组,即半干旱地区、半湿润地区和湿润地区。
(2)在单元格C35中输入“=COUNTIF(B2:B32,">800")”,按下Enter键,得到降水量在800毫米以上的城市数。
(3)计算降水量在400~800区间内的城市个数,在单元格C36中输入公式“=COUNTIF (B2:B32,"<=800")-COUNTIF(B2:B32,"<=400")”,按下Enter键,得到400~800区间内的数据个数。
(4)同理,在单元格C37中输入公式“=COUNTIF(B2:B32,"<=400")-COUNTIF (B2:B11,"<=200")”,按下Enter键,得到降水量在200~400区间内的城市数量,结果如图4-4所示。
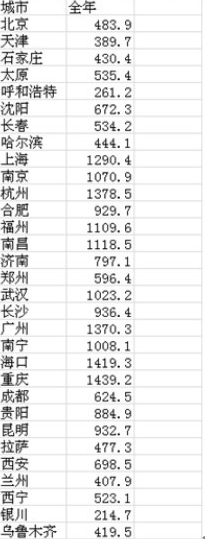
图4-3 实验
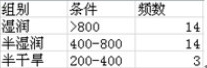
图4-4 实验4-2的分组结果
综上所述,分组结果有科学依据,连续型分组界限便最终确定。