




比较两个分数的大小,有两种基本方法,第一种是:如果两个分数分母相同,分子大的分数较大;第二种是:如果两个分数分子相同,分母小的分数较大。当分子、分母都不相同时,或统一分母,或统一分子,再进行比较。
但往往解题不会那么简单,有时我们会遇到分母特别大的时候,通分会不方便,这就需要我们采取作差法、相除法、交叉相乘法、倒数法、化为小数或循环小数等再进行比较,具体方法将在典型例题中一一讲解。
比较分数
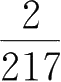 与
与
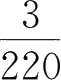 的大小。
的大小。
分析 由于分数的分母较大,可以先统一分子,再进行比较。
解
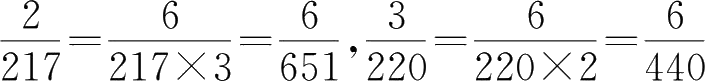 。
。
因为
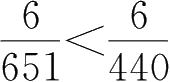 ,所以
,所以
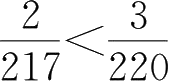 。
。
1.比较分数
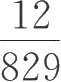 与
与
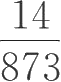 的大小。
的大小。
2.将下列分数按从小到大的顺序进行排列:
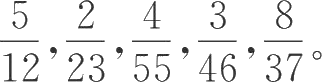
比较分数
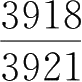 与
与
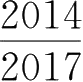 的大小。
的大小。
分析 由于分子、分母都比较大,采用统一分子和统一分母的方法都比较麻烦,所以我们采用作差法来比较两个数的大小。
解
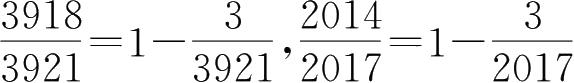 。
。
因为
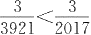 ,所以
,所以
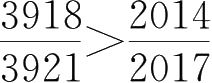 。
。
1.比较分数
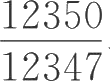 与23456的大小。
与23456的大小。
2.比较分数
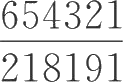 与
与
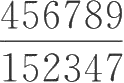 的大小。
的大小。
比较分数
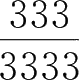 与
与
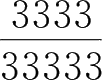 的大小。
的大小。
分析 先观察分子、分母,发现用倒数比较大小会比较容易。再遵循倒数大的原分数反而小的原理对原数进行比较。
解
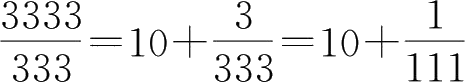 ,
,
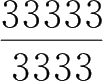 =10 +
=10 +
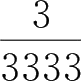 =10+
=10+
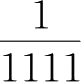 。
。
因为
 >
>
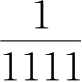 ,所以
,所以
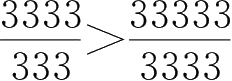 。
。
即
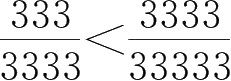 。
。
1.比较分数
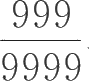 与
与
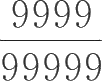 的大小。
的大小。
2.比较分数
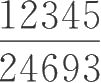 与
与
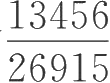 的大小。
的大小。
比较分数
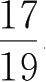 与
与
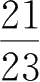 的大小。
的大小。
分析 这道题我们采用交叉相乘的方法来解题。
解
19×21=399,17×23=391,因为399>391,所以21所在的分数要比17所在的分数大,所以
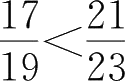 。
。
1.比较分数
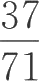 与
与
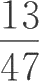 的大小。
的大小。
2.比较分数
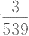 与
与
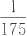 的大小。
的大小。