专题概述

在掌握三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等基本图形的面积计算公式的基础上，进行多边形的面积计算。本讲常见的解题方法有：

(1)对于多种基本图形的组合，利用已给的线段间的比例关系，求出多边形的面积；

(2)把图形进行切分、平移、翻转、补充、变形转化为基本图形，继而求出多边形的面积。

典型例题1

1.已知三角形ABC的面积为1,BE=2AB,BC=CD,求三角形BDE的面积。

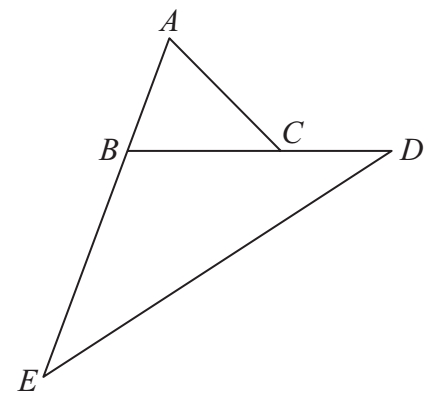
分析 利用已给的线段间的比例关系、三角形的面积以及三角形的面积公式，设法把三角形BDE划分成一些与三角形ABC的面积成相应比例的三角形。这样，三角形BDE的面积就能求得了。

解 见右图，连接CE。

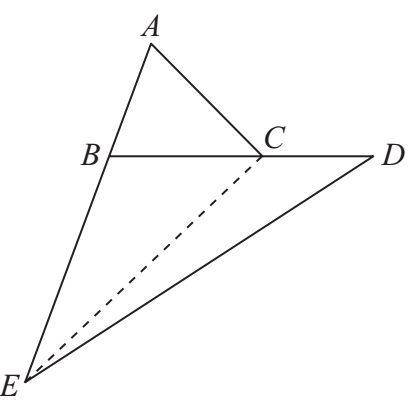
对于三角形ABC与三角形BEC,分别把AB和BE看成底，那么它们的高相等。此外,BE=2 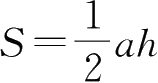可知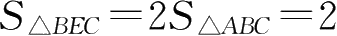， 。显然，三角形BEC和三角形CED是两个等底（BC=CD)、等高的三角形，因此 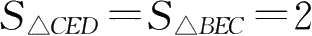。这样， 。

思维训练1

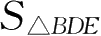
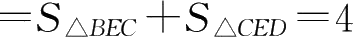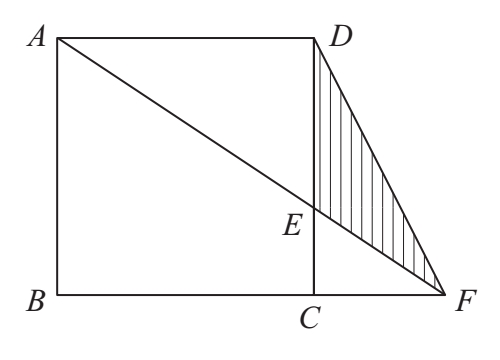
1.正方形ABCD的边长是18厘米，已知DE是EC长度的2倍，求三角形DEF的面积。

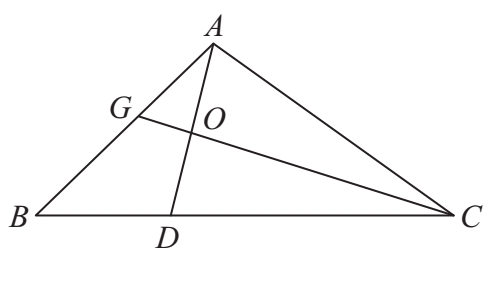
2.如图所示,DC=2BD,AO=OD,三角形AOG的面积与三角形DOC面积的和是16平方厘米。三角形ABC的面积是多少？

典型例题2

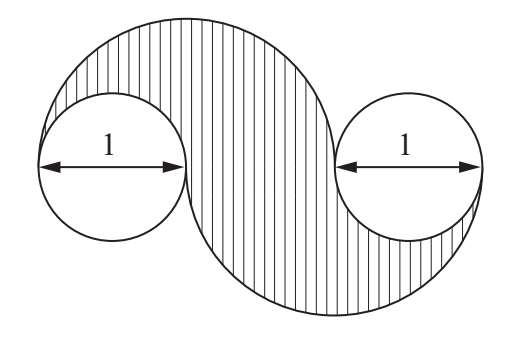
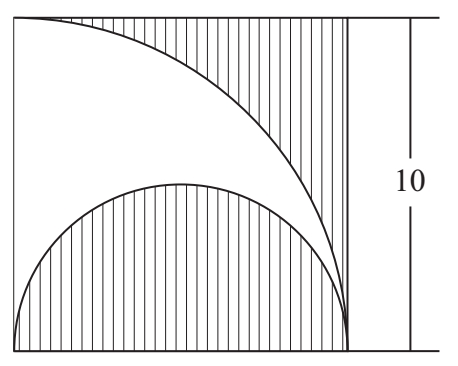
求图中阴影部分的面积。（大圆直径为2,单位：厘米，圆周率π取近似值3.14)

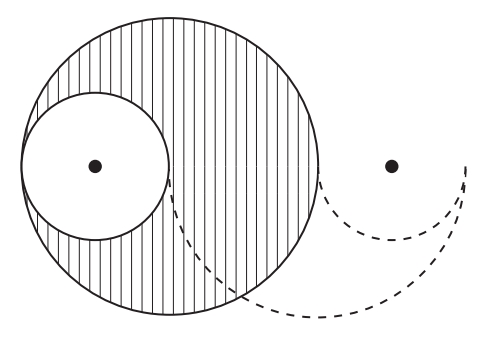
分析 如图所示，解题时可以先将图形下半部分翻转拼接，然后将图中的小圆移至中心。从图中不难看出，求原图中阴影部分的面积就是求一个圆环的面积。

解 大圆半径:2÷2=1(厘米），

小圆半径:1÷2=0.5(厘米），

阴影面积:3.14×(1 ² -0.5 ² )=2.355(平方厘米）。答：阴影部分的面积是2.355平方厘米。

思维训练2

1.如图，求阴影部分的面积。（圆周率π取近似值3.14)

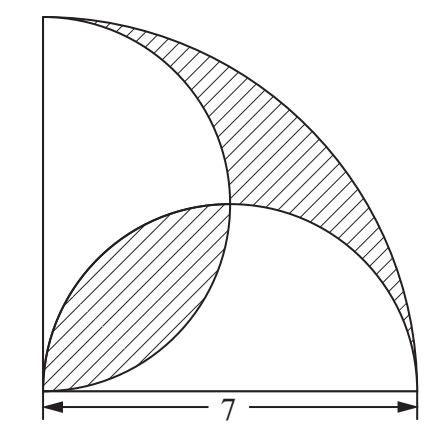
2.求图中阴影部分的面积。（单位：分米）

典型例题3

如图所示，一块长方形钢板，长截下4分米，宽截下1分米后，成了一块正方形钢板，面积比原来减少了49平方分米。原来长方形钢板的面积是多少平方米？

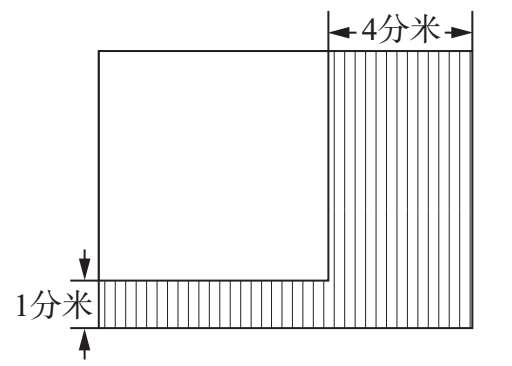
分析 初看起来，图中长方形长和宽，正方形的边长都不知道，无法求出长方形的面积，能否用特殊的方法思考呢？审题后发现长方形的长、宽和面积都和正方形有关系。对于图中的阴影部分，可以添一条“辅助线”，如图(1)或图(2)，把它分解成两个长方形。以图(2)为例。记正方形的边长为x分米。带阴影的小长方形长为（x+4)分米，宽为1分米，带阴影的大长方形长为x分米，宽为4分米。“面积比原来（长方形）减少了49平方分米”，也就是大长方形阴影部4分 面1积+小长方形阴影部分面积=阴影部分总面积=49平方分米，可以用方程解。

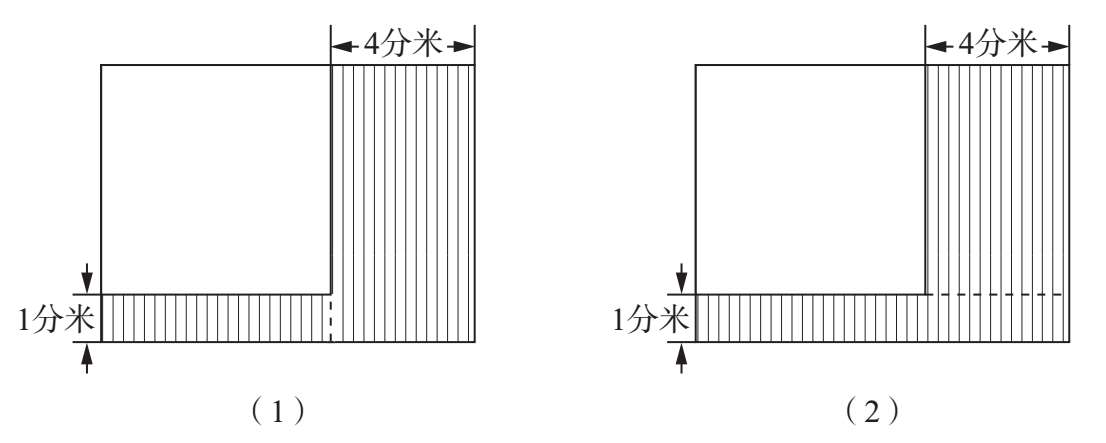
解 设正方形边长为x分米。

(x+4)×1+4x=49

x+4+4x=49

5x=45

x=9

9×9+49=130(平方分米）

答：长方形钢板面积为130平方分米。

思维训练3

1.某校将每年的三月份的第一周定为植树周。今年该校在市郊的一块如图(1)所示边长为100米的正方形山地上植树，图中的阴影部分是一个小水库。同学们要在每平方米内种一棵树，每天种树1075棵。问同学们几天能完成植树任务？（π取3.14)

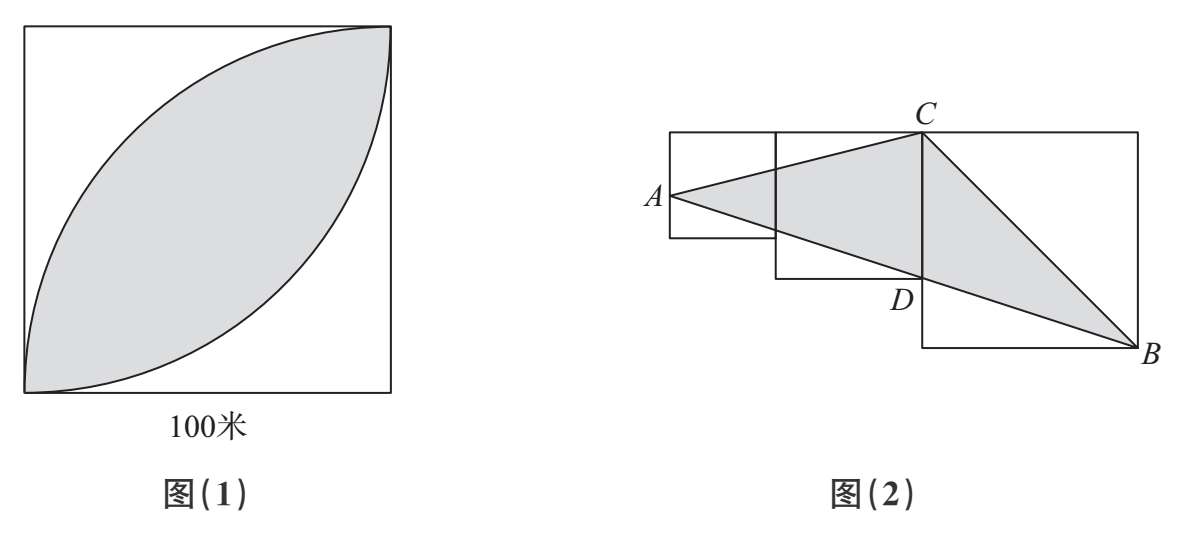
2.如图(2)，公园里有一片三个正方形相连的绿化带，三个正方形的边长分别是15厘米,20厘米,30厘米，绿化带中间有一个三角形花圃（阴影部分）。求这个三角形花圃的面积。 6aijA5/LWdmZ68xAIEnvTOcDlp6VnUziIEKNPJFFYDc4oFStQYnVhj0ZqWBv8UJj