




在面临长方体和正方体的面积、体积问题时,要注意单位的换算及公式的灵活运用。常见题型有:
(1)多个正方体拼接后得到长方体,求面积(或棱长和)的问题;
(2)求水池水深问题;
(3)长方体或正方体箱子的包装问题;
(4)容积问题;
(5)长方体、正方体面积、体积公式综合运用问题。
将七个完全相同的正方体组合成一个长方体后,棱长和为180厘米,原来每个正方体的棱长和是多少?
分析 每一个正方体有12条棱,七个共有12×7=84(条)棱,组合后共少了2×4+5×8=48(条)棱,即有36条棱,可求出每条棱的棱长,后求出棱长和。
解 七个正方体共有12×7=84(条)棱,组合后减少了2×4+5×8=48(条)棱,即组合后有36条棱,共180厘米长,因此每条棱长180÷36=5(厘米)。
原来每个正方体的棱长和为5×12=60(厘米)。
答:每个正方体的棱长和为60厘米。
1.将五个棱长是8厘米的正方体拼成一个长方体,这个长方体的表面积是多少平方厘米?
2.把一个棱长40厘米的正方体,分成五个完全相同的长方体,这五个长方体的表面积之和是多少平方厘米?
一个长方体水池,长50厘米,宽40厘米,高30厘米,里面装有12厘米深的水,把一个底面为边长20厘米的正方形的长方体铁块竖直放入玻璃缸,铁块还有一部分露出水面,这时水深多少厘米?
分析 由于铁块有一部分露出水面,利用公式体积=底面积×高,水的体积不变,可求水面高度。
解 水池里水的体积为50×40×12=24000(立方厘米),
铁块底面积为20×20=400(平方厘米),水池底面积为50×40=2000(平方厘米),
因此放入铁块后水深24000÷(2000-400)=15(厘米)。
答:这时水深15厘米。
1.一个长方体,如果高减少4厘米,就成为一个正方体。这时表面积比原来减少了96平方厘米。原来长方体的体积是多少立方厘米?
2.至少要几个小正方体才能拼成一个大正方体?如果一个小正方体的棱长是25厘米,那么大正方体的表面积是多少平方厘米,体积是多少立方厘米?
有一个礼盒需要用彩带捆扎,捆扎效果如图,打结部分需要15厘米彩带,一共需要多长的彩带?
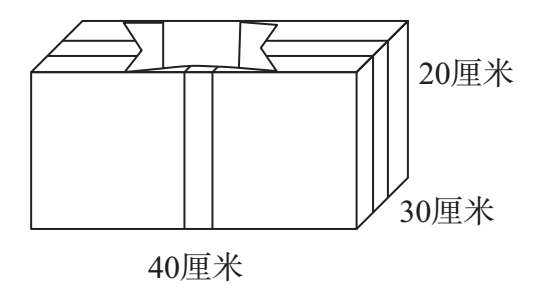
分析 本题虽然并未直接提出求棱长和,但由于彩带的捆扎是和棱相互平行的,因此,在解决问题时首先确定每部分彩带与哪条棱平行,通过求棱长和间接去求彩带长度。前面和后面的彩带长度=高的长度;左面和右面的彩带长度=高的长度;上面和下面的长的彩带长度=长的长度;上面和下面的短的彩带长度=宽的长度。需要彩带的长度=高×4+长×2+宽×2+打结部分长度。
解 20×4+40×2+30×2+15=235(厘米)
答:一共需要235厘米长的彩带。
1.一个长方体的纸包装箱,长30厘米,宽和高都是20厘米。做10个这样的包装箱,至少需要纸板多少平方厘米?合多少平方分米?
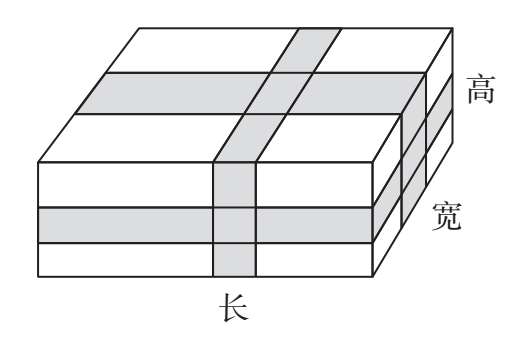
2.某工人在包装长方体箱子,使用麻绳在如图所示的三个方向上加固,麻绳长度分别为370,410,490厘米,如果麻绳之间接头重叠的部分都是10厘米,那么这个长方体箱子的体积是多少立方米?
有一个长为9分米,高为5分米,体积为270立方分米的硬纸盒,有一件陶瓷长为8.6分米,高为4.4分米,宽为6.2分米,是否可以放入该容器?
分析 只计算容器和陶瓷的体积,我们可以发现陶瓷体积<硬纸盒体积。但这并不意味着瓷器就可以装进盒子。我们还需要观察陶瓷长、宽、高与容器长、宽、高的大小。
解 硬纸盒的宽为270÷5÷9=6(分米),由于6分米<6.2分米,所以无法放入容器中。
答:不能放入容器中。
1.在一个棱长为5厘米的大立方体的顶部中央挖去一个棱长为2厘米的小正方体,现在这个大正方体的表面积是多少平方厘米?
2.把一个玻璃球放进一个底为12平方分米,高为7分米,水深3分米的长方体容器里后,水面升到离容器顶部2.6分米的位置,再放多少个球水将会溢出?