




|
|
|
|
蒯因(W·V·O·Quine),20世纪后半期美国哲学的领军型人物,也是同时期国际分析哲学界的代表性人物。在新近进行的一项国际性哲学调查中,他位列过去200年间最重要哲学家的第5位。
 蒯因首先是一位逻辑学家,在数理逻辑方面有很多建树;但更重要的是一位哲学家,他对逻辑哲学问题做了系统性探讨,提出了他自己的独创性理论;他还把数理逻辑运用到他的全部哲学研究中,发展了一个有统一主题和清晰脉络的哲学体系,“从逻辑和语言的观点看”是其哲学研究最鲜明的方法论特点之一。
蒯因首先是一位逻辑学家,在数理逻辑方面有很多建树;但更重要的是一位哲学家,他对逻辑哲学问题做了系统性探讨,提出了他自己的独创性理论;他还把数理逻辑运用到他的全部哲学研究中,发展了一个有统一主题和清晰脉络的哲学体系,“从逻辑和语言的观点看”是其哲学研究最鲜明的方法论特点之一。

傅伟勋曾提出“创造的诠释学”,主张在研究某位思想家的学说时,要依次考虑如下五个步骤或层面:(1)“实谓”:原作者实际上说了什么?(2)“意谓”:原作者真正意谓什么?(3)“蕴谓”:原作者可能说什么?(4)“当谓”:原作者本来应该说什么?(5)“创谓”:作为创造的诠释家,我应该说什么
 在本章中,我将把此方法应用到对蒯因逻辑哲学的系统探讨中。本章分三节:第一节讨论蒯因关于逻辑或逻辑真理究竟说了些什么,属于“实谓”和“意谓”层次;第二节分析蒯因的逻辑哲学遭遇到哪些难题、困境和悖论,可归于“蕴谓”层次;第三节探讨蒯因关于逻辑或逻辑真理本来应该再说些什么,属于“当谓”和“创谓”层次。我将遵循蒯因的自然化认识论的思路,发展出一种带有实在论和认知主义色彩的逻辑哲学。
在本章中,我将把此方法应用到对蒯因逻辑哲学的系统探讨中。本章分三节:第一节讨论蒯因关于逻辑或逻辑真理究竟说了些什么,属于“实谓”和“意谓”层次;第二节分析蒯因的逻辑哲学遭遇到哪些难题、困境和悖论,可归于“蕴谓”层次;第三节探讨蒯因关于逻辑或逻辑真理本来应该再说些什么,属于“当谓”和“创谓”层次。我将遵循蒯因的自然化认识论的思路,发展出一种带有实在论和认知主义色彩的逻辑哲学。
可以说,蒯因的逻辑哲学是他的自然化认识论的一部分,也是他关于知识或科学的整体主义的一部分。可以把他的逻辑观概括为如下11个论题。
T1.只有真值函项和带等词的)量化的逻辑才“逻辑”,视需要可将其称为“初等逻辑”、“谓词演算”、“量化理论”或“正统逻辑”。
在蒯因看来,逻辑有三个特征:(1)它是外延的。“我把两个闭语句称为共外延的,如果它们同真或同假。当然,两个谓词、普遍词项或开语句是共外延的,如果它们对于相同的对象或对象序列来说是真的。两个单称词项是共外延的,如果它们指称相同的对象。最后指出,一个表达式是外延的,如果用共外延的表达式替换其部分表达式总是得到一个共外延的整体。
外延主义
是外延理论的嗜好。”
 2)它是完全的。如果一个模式是有效的,那么它在逻辑系统中是可证的。(3)它有许多方法论甚至美学上的优点,例如方便性、有效性、优雅性、熟悉性、精致性、简单性等。
2)它是完全的。如果一个模式是有效的,那么它在逻辑系统中是可证的。(3)它有许多方法论甚至美学上的优点,例如方便性、有效性、优雅性、熟悉性、精致性、简单性等。
T2.真值函项和(带等词的)量化的逻辑为我们关于世界的知识体系提供了标准记法。
蒯因认为,“我们所面临的这个世界体系的构架,就是今天逻辑学家们十分熟悉的结构,即量化逻辑或谓词演算”
 ,“科学语言的基本结构,已经以一种熟知的形式被离析出来并得到系统化。这就是谓词演算:量化和真值函项的逻辑”
,“科学语言的基本结构,已经以一种熟知的形式被离析出来并得到系统化。这就是谓词演算:量化和真值函项的逻辑”
 。他十分关注本体论。为了揭示出一个科学理论的本体论承诺,我们不得不按照标准记法(即谓词演算的语言)改写这个理论,从而对该理论进行语义整编。然后,根据他的标准“存在就是成为约束变项的值”
。他十分关注本体论。为了揭示出一个科学理论的本体论承诺,我们不得不按照标准记法(即谓词演算的语言)改写这个理论,从而对该理论进行语义整编。然后,根据他的标准“存在就是成为约束变项的值”
 ,我们可以识别出该理论在本体论上所承诺的实体。最后,依据他的口号“没有同一性就没有实体”
,我们可以识别出该理论在本体论上所承诺的实体。最后,依据他的口号“没有同一性就没有实体”
 ,只有该理论提供了其所承诺的实体的个体化标准,我们才能接受这些实体。
,只有该理论提供了其所承诺的实体的个体化标准,我们才能接受这些实体。
T3.集合论被排除在逻辑的范围之外。
蒯因不把集合论看作逻辑,其中“∈”是初始谓词,类或集合是量化变元的值。不过,他把关于真类和关系的理论看作“伪装的逻辑”。他认为,“属于关系”(x∈a)不能还原为逻辑中的“谓述关系”(Fx)。在逻辑和集合论之间有三个重要区别:(1)逻辑是完全的,而集合论不是。从哥德尔不完全性定理可以推出,集合论在根本上是不可完全的。(2)逻辑是论题中立的,所以它没有本体论承诺,但是,由于集合论允许对类或集合进行量化,故它在本体论上承诺了类或集合的存在。(3)“集合论有许多种,其区别不仅在表述上而且在内容上:关于什么样的集合被说成是存在的。”
 相反,逻辑只有一种。我们虽然有不同的逻辑系统,但是它们并不在内容上不同,因为它们有相同的定理集或逻辑真理集。
相反,逻辑只有一种。我们虽然有不同的逻辑系统,但是它们并不在内容上不同,因为它们有相同的定理集或逻辑真理集。
T4.高阶量化理论不属于逻辑。
蒯因至少给出了两个理由:(1)从形式上说,逻辑是完全的,但是高阶量化理论不是完全的。也就是说,对于初等逻辑来说,逻辑真理集恰好是定理集,但是这种情形并不出现在高阶逻辑中。在他看来,这是所谓的“高阶逻辑”的一大缺陷。(2)逻辑就其本体论而言是中立的,但是高阶逻辑具有特殊的本体论承诺,例如,它允许对谓词和命题进行量化,所以它在本体论上承诺了抽象对象(例如,性质和命题)的存在。由于这些对象缺少个体化标准,蒯因拒绝承认它们作为抽象对象而存在。
T5.模态逻辑不应被看作逻辑。
众所周知,蒯因激烈地批判模态逻辑(即关于必然性和可能性的逻辑)和可能世界语义学。在他看来:(1)模态逻辑来源于混淆表达式的使用和提及,所以就其来源而言是不合法的。(2)模态语境是指称晦暗的,在其中同一替换规则和存在概括规则失效。模态逻辑失去了外延性。在蒯因看来,这是不能把它看作逻辑的最好理由。(3)为了处理模态语境的晦暗问题,我们不得不接受抽象对象,例如命题、性质和概念,这将造成很多棘手的哲学问题。即使如此,我们仍然不能摆脱困境,甚至还能通过证明p《□p使模态逻辑坍塌为初等逻辑。(4)模态逻辑将返回亚里士多德的本质主义,而蒯因将后者视为臭名昭著的柏拉图主义泥潭。因此,他拒绝模态逻辑和可能世界语义学,主张停留在标准语法(即量化逻辑)的范围内。
T6.没有必要发展关于命题态度词的逻辑。
蒯因断言,命题态度词(例如“认为”、“相信”和“希望”)导致指称晦暗语境,同一替换规则在其中失效。他考虑了对包含命题态度词的语句的几种可能解读,以“汤姆相信达尔文错了(Tom believes that Darwin erred)”为例:(1)承认如下构造,通过前置小品词“that”由语句形成单称词项。例如,“Tom believes that Darwin erred”被释义为三部分:Tom,believes和that Darwin erred。(2)承认如下构造,通过插入小品词“that”由二元谓词和语句形成一元谓词:Tom和believes that Darwin erred。(3)将“believes that”处理为新的词汇范畴——态度词,然后承认如下构造:通过把态度词“believes that”和语句“Darwin erred”连接起来形成一元谓词“believes that Darwin erred”。(4)承认如下构造,将语句看作其构成部分,并给出一元谓词。动词“believes”不再被视为一个词项,而是成为算子“believes[]”的部分(“[]”是内涵抽象记号),例如“Tom believes[Darwin erred]”。(5)通过语义上溯,把“Tom believes that Dar-win erred”看作“Tom believes‘Darwin erred’”、“Tom believes-true‘Darwin erred’”或者“Tom believes-true‘x erred’of Darwin”。蒯因拒绝(1)和(3),因为它们错误地把命题看作内涵实体。他偏向于(2)和(5),因为他讨厌的内涵实体(如命题)并不在其中出现。按照这种方式,他实际上消掉了态度词,只把它们看作逻辑标准语法的一般谓词,故没有必要再发展关于命题态度词的逻辑。

T7.关于逻辑真理的语言学理论是错误的。
根据语言学理论,逻辑真理是纯粹由于语言而真的,与我们生活于其中的世界毫无关系。具体地说,这个理论断言:(1)逻辑真理仅仅由于逻辑词项的潜在意义和使用而为真;(2)逻辑真理仅仅由于语言约定而为真。蒯因认为,即使(1)可能对于初等逻辑成立,它仍然没有解释力,因为我们可以通过其在行为方面的明显性或潜在明显性来解释逻辑真理,而不必诉诸(1)。(2)也不成立,因为如果我们通过约定而承认逻辑真理,我们就应该通过约定而承认任何学科的真理,也就是说,语言约定并不能区分逻辑真理和经验真理;还因为语言约定的证成(justification)不得不依赖于其他语言约定,这将导致循环论证和无穷倒退的谬误。蒯因指出,尽管逻辑理论极大地依赖于语言,但它并不是面向语言的,而是面向世界的。真谓词维持了逻辑学家与世界的联系,世界是他的注意力之所在。

T8.存在对逻辑真理的多种不同刻画。
在《依据约定为真》(1936)一文和《语词和对象》(1960)一书中,蒯因通过区分表达式的“本质出现”和“空洞出现”来刻画逻辑真理。在《逻辑哲学》(1970)一书中,他通过如下方式来定义逻辑真理:(1)根据结构:“一个语句是逻辑真的,如果所有分享其逻辑结构的语句都是真的。”(2)根据替换:“一个语句是逻辑真的,如果在改变其谓词的情况下它仍然是真的。”“逻辑真理被定义为这样一个语句,在用语句替换其简单部分时我们仍然只得到真。”(3)根据模型:“一个模式是有效的,如果它被它的所有模型满足。最后,逻辑真理是……任何可以在有效的模式中进行替换而得到的语句。”(4)根据证明:“如果我们选择这些证明程序其中之一……我们可以把逻辑真理简单定义为由这些证明规则产生的任何语句。”(5)根据语法:“一个逻辑真理是……其语法结构使得所有具有该结构的语句都为真的语句”,“逻辑真理是通过词汇替换而不会变为假的真理”
 。
。
在关于逻辑真理的这些定义中,蒯因预先假设了一个给定的逻辑词汇清单,使用了哥德尔完全性定理,把替换不变性置于重要位置,这些做法在某种程度上都是可被质疑的,有循环论证的嫌疑。
T9.逻辑真理具有三个显著特征。
蒯因指出:(1)逻辑真理在行为意义上是明显或潜在明显的。一个语句就其本身而言是明显的,如果在彻底翻译的语境下任何证据都直接地且毫不犹豫地支持这个语句,且在这样做时也不需要任何附加信息。一个语句是潜在明显的,如果它可以从明显的真理通过一系列单独明显的步骤而得到。(2)逻辑真理是论题中立的:它们缺少特殊的主题。“逻辑不偏爱词典的特别部分,也不偏爱变元值的这个或那个子域。”(3)逻辑真理是普遍适用的:“它[逻辑]是所有科学(包括数学在内)的婢女。”

T10.面对顽强不屈的经验,逻辑是可修正的。
根据蒯因的整体论,我们的知识总体或其中一个足够大的部分是被经验证据不充分决定的:它作为一个整体被经验证据所检验,其中的个别陈述不能被经验确定地证实或证伪。就其经验内容而言,知识体系内只有程度的差别:有些陈述或多或少地接近于观察边缘,比其他陈述具有或多或少的经验内容,不存在种类的不同:有些陈述具有经验内容,有些陈述没有。以这种方式,逻辑或数学陈述也具有它们的经验内容,仅仅就其是处于我们知识中距离感官证据较远的部分而言,它们不同于其他更接近于这些证据的陈述。在顽强不屈的经验面前,任何陈述都不能免于修正,即使逻辑或数学的陈述也不例外。
T11.不伤害或不修正逻辑总是一个合理的策略。
蒯因认为,虽然我们的知识体系作为整体面对经验法庭,但它仍然有其自身的结构,其中有不同部分和不同层次的差别。例如,有些部分或层次处于这个体系的观察边缘,具有较多的经验内容;其他部分或层次(例如逻辑和数学)处于这个体系的中心,具有较少的经验内容。在我们的认识和行动中,应该总是遵循最小损害原则。既然逻辑和数学处于我们知识体系的中心位置,远离观察和证据,倘若我们试图通过修正逻辑或数学来恢复系统的一致性,我们将做出代价很高甚至是很危险的选择,由此导致该知识系统的瓦解。因此,虽然逻辑是可修正的,但我们总是应该克制修正逻辑的冲动,而寻求别的解决问题之道。
除了T1~T11之外,蒯因还给出了关于逻辑或逻辑真理的其他观点,在下一节将予以讨论。
应该注意,如同康德试图把逻辑冻结在传统形式逻辑(其主要部分是亚里士多德的三段论和斯多亚派的命题逻辑)层次上一样,蒯因似乎试图把逻辑冻结在真值函项和量化的逻辑层次上,因为他并不接受任何其他版本的逻辑或逻辑分支。然而,当代逻辑的发展与蒯因的原初设想几乎背道而驰,可给出如下例证:
(1)由于卡尔纳普、康格尔、蒙塔古、普莱尔、亨迪卡、马库斯,尤其是克里普克的工作,模态逻辑及其可能世界语义学自从20世纪50年代以来取得了迅猛且成功的发展。在某种意义上,模态逻辑已经成为新的“经典”逻辑,可能世界语义学已经成为新的“经典”语义学:它们是发展新逻辑分支的必要的且强有力的工具。
(2)与蒯因的判断相反,命题态度词归属已经成为当代语言哲学、逻辑哲学、心灵哲学甚至形而上学和认识论领域内的热门话题。
(3)许多当代数学哲学家已经接受高阶逻辑,因为它对于发展数学理论来说是绝对必需的。例如,对某些数学哲学观点(如莱特的抽象主义和夏皮罗的结构主义)的论证都依赖于二阶逻辑。
(4)蒯因的集合论工作偏离了集合论的发展主流。请看如下评论:“……集合论的领军人物D·A·马丁在一篇评论文章中指出,虽然蒯因的《集合论及其逻辑》发表于1963年,那时ZF公理系统已被确定为标准系统多年(例如,它的一个版本或变体已被布尔巴基丛书的第一卷采纳),但该书对这个话题的处理似乎使人觉得,如何面对罗素悖论而继续发展集合论仍然是一个开放问题。”
 作为一位杰出的逻辑学家和哲学家,蒯因关于逻辑或逻辑真理的说法为什么会如此偏离当代逻辑的实际发展进程,甚至与其背道而驰呢?对于这个问题,我给出以下尝试性回答:蒯因给逻辑加上了太多的本体论重负,在逻辑和本体论之间施加了过于紧密的联系。如前所述,他提出了两个著名口号:“存在就是成为约束变项的值”,“没有同一性就没有实体”。在他的本体论中,遵循第二个口号,他愉快地接受了物理对象,有些不情愿地接受了类或集合的存在,但是他强烈拒绝承认内涵实体(例如命题)、抽象对象(例如性质)、可能个体等其他实体。主要出于本体论考虑以及方法论和美学上的偏好(例如完全性、简单性和优雅性),蒯因只把量化理论看作逻辑,却把集合论和高阶逻辑都排除在逻辑范围之外,忽视了发展一些新逻辑分支(如模态逻辑、时间逻辑、命题态度逻辑、反事实条件句逻辑等)的可能性。我认为,蒯因的这种做法是错误的,至少是值得商榷的。事实上,逻辑研究命题之间的推理关系,而这种关系只是假设性的:
如果
某个前提集是真的,
则
某个特定的结论也必须是真的。因此,逻辑是论题中立的,它可以适用于任何话语范围,甚至适用于完全虚构的话语范围。例如,关于魔鬼或外星人,我们也可以清楚地和理性地(即合乎逻辑地)谈论,互相交换有关它们的看法,不管我们是否承认它们确实在这个宇宙中存在。
作为一位杰出的逻辑学家和哲学家,蒯因关于逻辑或逻辑真理的说法为什么会如此偏离当代逻辑的实际发展进程,甚至与其背道而驰呢?对于这个问题,我给出以下尝试性回答:蒯因给逻辑加上了太多的本体论重负,在逻辑和本体论之间施加了过于紧密的联系。如前所述,他提出了两个著名口号:“存在就是成为约束变项的值”,“没有同一性就没有实体”。在他的本体论中,遵循第二个口号,他愉快地接受了物理对象,有些不情愿地接受了类或集合的存在,但是他强烈拒绝承认内涵实体(例如命题)、抽象对象(例如性质)、可能个体等其他实体。主要出于本体论考虑以及方法论和美学上的偏好(例如完全性、简单性和优雅性),蒯因只把量化理论看作逻辑,却把集合论和高阶逻辑都排除在逻辑范围之外,忽视了发展一些新逻辑分支(如模态逻辑、时间逻辑、命题态度逻辑、反事实条件句逻辑等)的可能性。我认为,蒯因的这种做法是错误的,至少是值得商榷的。事实上,逻辑研究命题之间的推理关系,而这种关系只是假设性的:
如果
某个前提集是真的,
则
某个特定的结论也必须是真的。因此,逻辑是论题中立的,它可以适用于任何话语范围,甚至适用于完全虚构的话语范围。例如,关于魔鬼或外星人,我们也可以清楚地和理性地(即合乎逻辑地)谈论,互相交换有关它们的看法,不管我们是否承认它们确实在这个宇宙中存在。
在蒯因的逻辑哲学中,有许多矛盾、冲突甚至悖论,其中最明显的是他关于逻辑所说的和所做的之间的鸿沟。在理论上,蒯因严肃地坚持逻辑的可修正性;在实践中,他却是极端保守的:只把关于真值函项和量化的理论看作逻辑,不承认对经典逻辑做实质性修正的任何变异逻辑是真正的逻辑,甚至不承认它们是对经典逻辑的真正修正。下面,我将讨论蒯因哲学中的四个“悖论”,包括卡茨的可修正性悖论,可修正性和坏翻译的悖论,可修正性和变异的悖论,以及用逻辑修正逻辑的悖论。根据我的分析,对于蒯因的逻辑哲学来说,其中的两个悖论是真实的,其他两个悖论则是表面的和虚假的,可以被解释掉。
1.卡茨的可修正性悖论
卡茨(Jerrod J·Katz)发现,有三个原则处于蒯因整体主义认识论的核心,即不矛盾原则(NC)、普遍可修正性原则(UR)以及简单性原则(S
 。然而,我倾向于把简单性原则替换为实用准则(PMs),因为实用准则更准确地反映了蒯因关于理论评价和选择的立场。因此,我们得到如下三个原则:
。然而,我倾向于把简单性原则替换为实用准则(PMs),因为实用准则更准确地反映了蒯因关于理论评价和选择的立场。因此,我们得到如下三个原则:
NC
:“……整个科学是一个力场,其边界条件是经验。与边缘经验的冲突导致力场内部的重新调整。对我们的某些陈述必须重新分配真值。”

UR
:“经验意义的单位是整个科学……如果我们在系统的其他地方做出足够巨大的调整,那么在任何情况下任何陈述都可以被认为是真的……相反……没有任何陈述是免于修正的。甚至排中律这一逻辑规律的修正已经被提议为简化量子力学的方式。”

PMs
:在评价或选择假说或理论时,我们必须考虑它们是否具有保守性、谦和性、简单性、概括性和可反驳性这些特征。

卡茨指出,第一个原则是说,在什么时候“必须”修正我们的信念系统:“若出现不一致,就要求修正”;第二个原则是说,我们在哪里进行修正:“该系统的任何陈述都不能免于修正”;第三个原则是说,我们应该如何修正:“它提供了在与经验冲突时最好去修正哪些陈述。”
 他强调,这些原则是蒯因整体主义认识论的构成性原则。然而,如果把它们放在一起,将会产生可修正性悖论:“由于这些原则是赞成信念修正的每个论证的前提,所以就一个支持信念修正的论证而言,不可能修正它们中的任何一个,因为修正它们中的任何一个都锯掉了这个论证所依赖的躯干。任何改变这些构成性原则真值的论证都必然得到与这个论证的某个前提相矛盾的结论,而且必然是关于修正这些构成性原则的不可靠论证。”
他强调,这些原则是蒯因整体主义认识论的构成性原则。然而,如果把它们放在一起,将会产生可修正性悖论:“由于这些原则是赞成信念修正的每个论证的前提,所以就一个支持信念修正的论证而言,不可能修正它们中的任何一个,因为修正它们中的任何一个都锯掉了这个论证所依赖的躯干。任何改变这些构成性原则真值的论证都必然得到与这个论证的某个前提相矛盾的结论,而且必然是关于修正这些构成性原则的不可靠论证。”

卡茨考虑了这个悖论的一个特例。假定UR、NC在原则上是可修正的。如果它是可修正的,那么存在一个可能的对其进行再评价的信念修正论证。但是,因为NC是一个构成性原则,它必然作为这个论证的前提出现。然而,如果在系统中正确地修正一个信念,该信念是完全错误的,那么它就不能是一个可靠论证的一部分。修正信念的论证就是不可靠的,没有为修正提供任何根据。因此,不存在任何修正NC的可靠论证,它是不可修正的。然而,因为所有信念都是可修正的,NC也必然是可修正的,因此,它既是可修正的又是不可修正的。他得出如下结论:“无限制的普遍性允许应用于自身的危险步骤,是悖论的熟知特征。把信念修正的认识论应用于自身,由此得到一个不可修正的可修正原则。因此,正如理发师悖论证明,不存在一个实际的理发师,他给那些且只给那些不给自己刮胡子的人刮胡子,可修正性悖论证明,不存在一个实际的认识论,它宣称一切东西包括它自己都是可修正的。”

一些学者有启发性地但也有争议地回应了这个悖论。
 我本人的回应是:该悖论是虚假的,论证如下:
我本人的回应是:该悖论是虚假的,论证如下:
(1)在讨论蒯因的可修正性论题时,我们应特别注意他本人使用的语词,例如:“readjustment”(再调整)、“redistribution”(再分配)、“reevaluation”(再评价)、“retract”(撤销)、“rescind”(废除)、“exempt”(免除)、“restore”(恢复)、“refute”(反驳)、“reject”(拒绝)等等。
 我将澄清蒯因的“可修正的”一词的如下确切涵义:
我将澄清蒯因的“可修正的”一词的如下确切涵义:
(i)加强或削弱。这两个词非常接近于蒯因的语词“再调整”“(真值的)再分配”“再评价”。当发现我们的理论与感官证据相冲突时,为了消除冲突且恢复一致,我们不得不首先在理论中进行调整,例如:把某些断言从存在陈述加强为全称陈述,或者从边缘陈述加强为核心陈述;相应地,把某些断言从全称陈述削弱为存在陈述,或者从核心陈述削弱为边缘陈述。
(ii)纳入、废除和替换。为了消除经验的反抗,我们把新的辅助假设加入理论中:“我们总是可以通过把恰当的前提明确地纳入S中来提供更为实质性的结论。”
 我们可以把某些陈述从理论中废除或撤销,让它们消失;也可以在系统中引入新陈述去替换掉旧陈述。
我们可以把某些陈述从理论中废除或撤销,让它们消失;也可以在系统中引入新陈述去替换掉旧陈述。
(iii)否定,这接近于蒯因自己的语词“反驳”和“拒绝”。用卡茨的解释,修正“在于把一个陈述从标记为真变成标记为假”
 ,或者(在我看来还应加上)把一个陈述从标记为假变成标记为真。也就是说,我们否认、反驳或拒绝一些原有陈述,把它们的真值从真改变为假,或者从假改变为真,或者将其转变成新形式,把后者保留在系统中。
,或者(在我看来还应加上)把一个陈述从标记为假变成标记为真。也就是说,我们否认、反驳或拒绝一些原有陈述,把它们的真值从真改变为假,或者从假改变为真,或者将其转变成新形式,把后者保留在系统中。
蒯因提纲挈领地阐述了如何去修正我们的理论:我们的理论蕴涵一个失效的观察断言句,我们不得不修补这个漏洞。在修补时,我们并不是只有一种选择,而是有很多选择,并且以简单性和最小损害原则为指导。我们按照这种方式进行尝试,直到有问题的蕴涵被消除。这就是他的整体论和可修正性论题的核心内容。

在重新表述他的可修正性悖论时,卡茨只考虑了两种修正方式:(1)“一个陈述从标记为真变成在系统中消失”,以及(2)“把一个陈述从标记为真变成标记为假”
 ,而且他更关注于(2)。即使他的论证在这些情况下是成立的,他仍然不能得到他的结论,因为他忽视了修正的其他情况,即加强、削弱、纳入和替换。很难证明,这四种情况也会导致可修正性悖论。
,而且他更关注于(2)。即使他的论证在这些情况下是成立的,他仍然不能得到他的结论,因为他忽视了修正的其他情况,即加强、削弱、纳入和替换。很难证明,这四种情况也会导致可修正性悖论。
就“可修正性”这个语词而言,我认为,克莱凡和埃尔斯坦分别犯了比卡茨更为严重的错误:他们都把“修正”等同于“否定”,即把“p被修正”等同于“¬p”。让我们看看柯里文的论证:
让我们把普遍可修正性(R)形式化为(∀x)◇Rx,其中Ra=“a被修正”,那么,这个论证是这样得出矛盾的:
1.(∀x)◇Rxw 1 (普遍可修正性)
然而,如果我们把1应用于它自身,并且把“被修正”读为接受其否定,则我们得到:
2.◇¬(∀x)◇Rxw 1 (在1中例示为1)
3.(∃x)□¬Rxw 2 (由2)
4.□¬Raw 2 (在3中例示为a)
5.◇Raw 1 (在1中例示为a)
6.Raw 3 (由5)
我们可以得到矛盾:
7.¬Ra w 3 (由4)
假设w
2
可通达w
3
。只有通达关系在像S5(D5或K5)这样的逻辑中是传递且对称的情况下,这个假设才成立。

克莱凡的结论是:关于认识论的恰当模态系统不能像S5一样强,这有令人信服的论证,故我们不应采取与S5一样强的认知逻辑,因此,卡茨的论证不成立,得不出他的“可修正性悖论”。按照与克莱凡类似的方式,我也可以得出结论:如果不把“p被修正”等同于“¬p”,那么(∀x)◇Rx并不蕴涵◇¬(∀x)◇Rx,克莱凡的论证就坍塌了。
埃尔斯坦宣称发现了一个新的可修正性悖论。他的论证非常简单。假定蒯因的一个原则UR:在经验面前任何信念在原则上都是可修正的;UR蕴涵ER:在经验面前有些原则是可修正的。因为ER也是我们的一个信念,所以它也是可修正的:“我们现在得到某种类似于悖论的方法。发现一个具有如下性质的信念:修正这个信念导致一个新的信念集,这个信念集禁止先前的修正。最明显的信念就是可修正性的存在断言(ER)……
在修正E R时考虑如下情况
:
得到的信念集包含¬E R
,
因此它禁止任何修正
。但是从修正后的角度看,人们不能把修正看作是得到证成的。当然,事先已经知道,任何对ER的修正都没有得到事后的证成。”

在埃尔斯坦的论证中,关键的步骤是让“ER被修正”等同于“¬ER”。根据我对“可修正的”一词的澄清,这个步骤是不合法的或无效的,因此,他所谓的“新的可修正性悖论”是子虚乌有的。
(2)我们应该严肃地对待蒯因的隐喻“力场”(a field of force)、“力场的边缘”(the periphery of the field)、“力场的内部”(the interior of the field)等等。
 按照我的理解,通过这些隐喻,蒯因强调了下面一点:尽管我们的知识或科学的各个部分连为一体,但其中仍可区分出不同的层次和复杂的结构。我这里把蒯因的隐喻转化为另一个隐喻:知识的金字塔。如下图示:
按照我的理解,通过这些隐喻,蒯因强调了下面一点:尽管我们的知识或科学的各个部分连为一体,但其中仍可区分出不同的层次和复杂的结构。我这里把蒯因的隐喻转化为另一个隐喻:知识的金字塔。如下图示:

所有这些项目构成了我们关于世界知识的整体,其中哲学(例如形而上学和认识论)也被包含进来,因为“自然主义哲学与自然科学是连续的”
 ,“哲学家和科学家在同一条船上”
,“哲学家和科学家在同一条船上”
 。这些项目仅有程度的差别:距离感觉刺激或远或近,经验内容或多或少,抽象程度或高或低,等等,而非种类的不同。
。这些项目仅有程度的差别:距离感觉刺激或远或近,经验内容或多或少,抽象程度或高或低,等等,而非种类的不同。
显然,蒯因承认知识整体中的这些项目是有区别的,例如有些陈述处于核心,有些处于边缘;有些处于抽象和普遍的层面;有些处于具体和特殊的层面;等等。按照这种方式思考,卡茨提到的三个构成性原则(即NC、UR和PMs)可能处于与我们的经验理论不同的层次上:经验理论是由关于外部世界的所有断言构成的,而构成性原则是关于这些理论的断言;换言之,经验理论是对象理论,而三个原则是关于它们的元理论,所以它们是关于如何修正经验理论的指导原则。
蒯因曾经明确表达了层次的观念。例如,为了消除冲突和反抗,“现在S中的某个或更多语句将不得不废除。我们免除S中的某些成员,因为不借助它们,这个重要的蕴涵关系仍然成立。因此,任何纯粹逻辑真理都是可免除的,因为无论如何,这些逻辑真理并没有为S逻辑蕴涵的东西增加任何东西”
 。也就是说,如果前提集S和逻辑一起蕴涵Q,那么集合S本身也蕴涵Q。逻辑承担着蕴涵关系。“这里我诉诸蕴涵:一簇语句蕴涵观察断言句。在这样做时,
我赋予逻辑一种特殊地位
:
逻辑蕴涵是理论和实验之间的纽带。
”
。也就是说,如果前提集S和逻辑一起蕴涵Q,那么集合S本身也蕴涵Q。逻辑承担着蕴涵关系。“这里我诉诸蕴涵:一簇语句蕴涵观察断言句。在这样做时,
我赋予逻辑一种特殊地位
:
逻辑蕴涵是理论和实验之间的纽带。
”
 从这些引文容易看出,蒯因相信逻辑是经验理论的基础或者超越于经验理论之外。
从这些引文容易看出,蒯因相信逻辑是经验理论的基础或者超越于经验理论之外。
通过蒯因隐含承认的陈述或理论的层级,我们可以避免卡茨的可修正性悖论:面对顽强不屈的经验,我们首先选择修正关于世界的理论中较为经验化的部分;如果这个策略行不通,我们可以选择修正我们的逻辑和数学;如果这仍然行不通,我们可以选择修正我们关于科学的哲学,其中包括那些构成性原则,如NC、UR和PMs。我们按照这种方式不断尝试:一个步骤接着另一步骤,一个部分接着另一部分,一个层次接着另一层次。
我的分析非常接近于塔明戛和维海格的分析。
 利用他人发展的基于认知保护带(epistemic entrenchment)的信念修正逻辑,他们论述说,卡茨错误地假定了构成性原则是关于世界的整体论的经验主义理论的内部陈述;实际上,最好把构成性原则看作关于科学探究的整体论的经验主义理论的属性。如果没有卡茨的那个错误假定,就无法得出他的可修正性悖论。
利用他人发展的基于认知保护带(epistemic entrenchment)的信念修正逻辑,他们论述说,卡茨错误地假定了构成性原则是关于世界的整体论的经验主义理论的内部陈述;实际上,最好把构成性原则看作关于科学探究的整体论的经验主义理论的属性。如果没有卡茨的那个错误假定,就无法得出他的可修正性悖论。
不过,为防止误解,我还要补充说,虽然在范围和层次上相互不同,我们知识的所有项目仍被连接为一个整体,与观察或感官证据相关联,因此,整体中的任何项目(包括逻辑和数学)仍然分享或多或少的经验内容,面对顽强不屈的经验在原则上都是可修正的。与此同时,对知识整体的任何修正都必须具有合理的证成,必须在不同的层次、部分、片段中进行,并且是分步骤进行的。利用罗尔斯所提出的来回往返法(back-and-forth),在修正科学总体时,我们最终将达到“反思的均衡”(reflective equilibrium)。
2.可修正性和坏翻译的悖论
这个悖论涉及蒯因的逻辑可修正性论题与他关于逻辑在翻译中的特殊地位的断言相冲突。
在谈论翻译时,蒯因通常指不同语言和文化之间的翻译,特别是指其极端情况:彻底翻译(radical translation),即语言学家把事先一无所知的丛林语言翻译为他们的母语。为了完成这项工作,语言学家不得不进入说这种语言的丛林部落,与这个社群生活在一起,与其中的成员交朋友,如此等等。假设有一个叫作“约翰”的语言学家,他来到某个部落,通常按如下方式进行翻译:
(1)观察这个部落的人在什么情境下说什么话,以及其他人如何回应他的话。(2)移情:约翰设想,如果他处于这些人的位置,他将会说什么和怎么说。(3)善意原则:约翰尽可能把部落的人看作与他和他自己的社群相似,如友善、温和、真诚、理性、在大多数情况下说真话,等等。
(4)“保持明显”的准则:“翻译的一个准则是,如果所断定的句子明显有错误,那多半在于有一些隐而不显的语言差别。”
 “在理解一种陌生语言时,我们应该做的是使那些明显的语句转变成真的,最好还是明显的英语句子。”
“在理解一种陌生语言时,我们应该做的是使那些明显的语句转变成真的,最好还是明显的英语句子。”
 5)逻辑真理特别是那些包含逻辑常项的真理是明显的或潜在明显的,所以在把丛林语言翻译为他的语言时,约翰应该把他的逻辑施加于丛林部落。约翰让逻辑成为翻译手册的一部分。根据他的手册,丛林部落将赞同所有的经典重言式,反对所有的经典矛盾式。
5)逻辑真理特别是那些包含逻辑常项的真理是明显的或潜在明显的,所以在把丛林语言翻译为他的语言时,约翰应该把他的逻辑施加于丛林部落。约翰让逻辑成为翻译手册的一部分。根据他的手册,丛林部落将赞同所有的经典重言式,反对所有的经典矛盾式。
(6)因此,在丛林语言的翻译中不能违反我们的逻辑规律。一个丛林人表面上反对形如“p或非p”的语句,或表面上赞同形如“p且非p”的语句,这就意味着我们的翻译出错了,我们做了坏的翻译甚至是荒谬的翻译。
(7)蒯因的结论是:很可能存在前逻辑文化,但是肯定不存在逻辑外或非逻辑的文化。“我们看到,两种文化的逻辑至多是不可比较的,却从不处于冲突之中,因为冲突将会使我们的翻译不可靠。”

于是,我们得到蒯因逻辑哲学中的第二个悖论:
P1.根据蒯因的整体主义,逻辑是可修正的。
P2.根据他关于彻底翻译的论证,逻辑是不可修正的。
结论:逻辑既是可修正的又是不可修正的。
这个悖论的根源是什么?如何消解它?我们有两个选择:第一个是否认P1,第二个是否认P2。我不喜欢第一个选择,因为我真诚地信奉蒯因的自然化认识论及其大多数结论,特别是其整体主义知识论。因此,我决定拒斥P2。
根据我的看法,善意原则和“保持明显”的准则是蒯因关于翻译的论证中最成问题的,而且它们之间有密切关联:“‘保持明显’的准则禁止把外族人表征为与我们的逻辑相矛盾(可能除复合语句中可改正的混乱之外)的任何翻译手册”,“我的意思仅是,在逻辑与翻译的不可分性中不存在
附加的
意味。无论其原因如何,明显性都足以说明这种不可分性”。“逻辑与翻译不可分,正如任何明显的东西都与翻译不可分。”

善意原则亦称“最大一致原则”。在我看来,这只是一个实用原则,并没有被充分证成,更别提是绝对确定的了。我们可以想象某种情形,其中这个原则不仅是错误的,甚至是危险的和灾难性的。在这个世界上,确实存在着恶棍、灵媒、魔鬼、精神病人、精神变态者、巫师、纳粹分子以及食人部落等。至少在某些情形中,他们并不像我们那样正常和有理性,他们可能以完全不同于我们的方式行动和思考。例如,丛林部落有可能遵循三值逻辑:当知道某个说法为真时表示同意,当知道该说法为假时表示反对,当不知道其为真为假时则沉默不语。在这种情况下,如果“非p”对其成员来说意味着p是假的,那么他们否认形如“p或者非p”的语句并不十分荒谬。这个部落也有可能是思维浅薄的,只要能够满足他们的当下要求,他们乐于在一个场合持有信念p,而在另一场合持有信念¬p,也就是说,他们乐于持有相互冲突的信念。
“保持明显”的准则甚至是更成问题的,因为我们不知道“明显”一词究竟意味什么。“明显——易于看到或理解;清楚的、显然的”[Obvious—easy to see or understand;plain,evident.(《韦伯斯特新世界词典》)],但是此定义没有解释任何东西。关于这个语词的任何解释都易于导致分歧和争论。我们认为有些东西是非常明显的,但是其他人并不这样认为。想象这样一个情形:你与一个丛林人聊天,他是这个部落的巫师,但是你不知道这个事实。突然间,开始下雨。这个人欢快地呼喊:“Nala hama gutai!”根据善意原则和“保持明显”的准则,你猜想他是在说:“下雨了!”或者“终于下雨了!”但他实际上在说:“神出现了!”或者“神来了!”最好还是引用蒯因自己的例子:甚至在面对行为证据的实指层面上,我们都不能分辨土著语词“gavagai”的正确翻译是什么:是兔子、兔子的片段、兔子的未分离部分、兔性,还是其他?这就是蒯因的著名论题——“指称的不可测知性”。如果甚至在实指层面上都不能达到明显性,我们还能指望在更为普遍和抽象的层次上达到它吗?
3.可修正性和变异的悖论
蒯因认为,变异逻辑其实并不是正统逻辑(即经典逻辑)真正的竞争对手,因为它们与经典逻辑表面上的不相容可以解释为相关逻辑联结词发生意义改变的结果。他宣称:“……当某人采纳一种其规律与我们的逻辑规律明显相反的逻辑时,我们宁愿猜想他只是把新的意义赋予一些熟悉的词汇(‘并且’‘或者’‘非’‘所有’等等)。”
 在反思关于矛盾律的争论时,他的评论是:“我关于这个对话的观点是,两边都不知道他们在谈论什么。他们认为他们在谈论否定、‘~’、‘非’;但是,当他们把‘p·~p’这样的合取式看作是真的,并且不把这种语句看作蕴涵所有其他语句时,这个记号无疑不再被视为否定。
很明显
,
变异逻辑学家在这里陷入了困境
:
当他试图否定这个学说时,他只是改变了主题
。”
在反思关于矛盾律的争论时,他的评论是:“我关于这个对话的观点是,两边都不知道他们在谈论什么。他们认为他们在谈论否定、‘~’、‘非’;但是,当他们把‘p·~p’这样的合取式看作是真的,并且不把这种语句看作蕴涵所有其他语句时,这个记号无疑不再被视为否定。
很明显
,
变异逻辑学家在这里陷入了困境
:
当他试图否定这个学说时,他只是改变了主题
。”

我把蒯因关于变异的论证重新表述如下:
(1)如果存在变异,则肯定存在相关逻辑联结词的意义改变。
(2)如果存在逻辑联结词的意义改变,就不存在变异逻辑与经典逻辑之间的真正冲突和对立。
(3)结论:在变异逻辑和经典逻辑之间没有真正的冲突和对立,因为在变异逻辑中显然存在逻辑联结词的意义改变。
因为变异逻辑是对经典逻辑的现成仅有的“修正”,如果它们不是对经典逻辑的真正修正,那么我们将面临一个困境:或者“逻辑是可修正的”是一句空话,或者逻辑本身是不可修正的。由此,我们得到蒯因逻辑哲学中的第三个悖论:
P1.根据蒯因的整体论,逻辑是可修正的。
P2.根据他关于变异的论证,或者“逻辑是可修正的”是一句空话,或者逻辑是不可修正的。
C.逻辑既是可修正的又是不可修正的。
我不接受蒯因关于变异逻辑的论证,所以我不接受上述P2,我也不认为这个悖论是真实的悖论,但它对于蒯因的逻辑哲学来说是 真实的 ,如果蒯因不改变他关于变异逻辑的观点的话。就变异逻辑和经典逻辑的关系而言,我持有如下两个主要观点:(i)在变异逻辑和经典逻辑之间,当然有逻辑联结词的某种意义改变,但是这种改变并不是完全的和彻底的,以至于像蒯因所断定的那样,变异逻辑完全改变了主题,因而在谈论与经典逻辑所谈论的不同的东西。(ii)在变异逻辑学家和经典逻辑学家之间有实质性的分歧、冲突和竞争,但是这种冲突和对立并不是全局的和总体性的,而是局部的和部分的。因此,变异逻辑和经典逻辑仍然有某些共同之处,我们可以在语法和语义上对它们做比较,甚至可以用某种方式把其中之一翻译成另一种。
对蒯因关于变异的论证中(1)的最明显论证将诉诸如下论题:逻辑联结词的意义完全是由包含它们的系统的公理或推理规则给出的。由这个论题大概可以得到,采用一个变异公理集蕴涵着其联结词的意义改变。但是,这个论题已经受到普莱尔的联结词“tonk”的挑战。他设计了一个包含联结词“tonk”的系统,遵循如下引入规则和消除规则:
A┣A tonk B
A tonk B┣B
普莱尔试图用这个系统表明,联结词的意义不能由系统的公理或推理规则给出。可以看到,“tonk”的两个规则既不是语法上恰当的,因为它们允许A┣B,也不是语义上恰当的,因为无法给出与这两个规则一致的唯一真值表。既然这两个规则是不可接受的,它们不能给出“tonk”的意义也就不足为奇了。我引用哈克的断言:“联结词的意义被看作,一部分来自它们在其中出现的系统的公理和规则及其形式语义,一部分来自赋予这些联结词的非形式解读以及形式语义的非形式解释。”

另外,哈克认为,即便如此,意义是由公理或推理规则给出的这一论题是否支持(1),这仍然是可质疑的。因为变异系统的典型情形是:它们的公理或规则非常接近于但不完全等同于经典逻辑的公理或规则,所以联结词在变异系统中的意义部分地而非完全地不同于它们在经典逻辑中的意义。她还认为,无论如何,对“变异逻辑必定包含意义改变”这一点并没有给出合理的一般性论证。

针对蒯因关于变异的论证中的(2),我将引用两个论证说明,联结词的意义改变并不足以表明,在变异逻辑与经典逻辑之间没有实质性对立。
哈克考虑了如下情况:一个变异逻辑学家D否认合式公式“(p∨q)→(¬p→q)”是逻辑真理。经典逻辑学家C却把这个合式公式看作定理。后来发现D用“∨”所指的正是C用“&”所指的东西。由此可得,当D反对“(p∨q)→(¬p→q)”是逻辑真理时,他所反对的不是C在断定“(p∨q)→(¬p→q)”是逻辑真理时所断定的东西。但是不能由此得出,在C和D之间就不存在实质性分歧,因为C也认为“(p∨q)→(¬p→q)”是逻辑真理。所以当D否认“(p∨q)→(¬p→q)”是逻辑真理时,他所否认的仍然是C所接受的东西。

威廉姆森重新发现了一个原本被卡尔·波普尔证明过的结论,与下面的意义改变论题相反:经典逻辑学家与直觉主义逻辑学家之间的区别仅仅是语词上的,因为他们把不同的意义赋予相关的逻辑词语,故他们在谈论不同的东西。他认为:“如果争议是口头的,那么我们需要消除那些逻辑词的歧义,比如区分经典否定‘并非
C
’和直觉主义否定‘并非
I
’。此时的图景是,每一方关于自己的话都是对的:‘并非
C
’的逻辑是经典的,而‘并非
I
’的逻辑是直觉主义的。因此,特别地,由于双重否定在经典逻辑中可消去,‘P是并非
C
并非
C
真的’应该蕴涵‘P是真的’;与此不同的是,双重否定在直觉主义逻辑中通常不能消去,‘P是并非
I
并非
I
真的’不应该蕴涵‘P是真的’。在此图景下,只要从符号上区别开来,‘并非
C
’和‘并非
I
’可以在同一语言中和平共处的逻辑原则就足够强以至于蕴涵了‘并非
C
’和‘并非
I
’等价,所以‘并非
C
’满足双重否定律,仅当‘并非
I
’也满足该定律。于是,和平共处是不可能的。经典逻辑与直觉主义逻辑之间的争议是真正的争论,而不只是口头上的。我将这种思考方式推广到与其他逻辑词有关的问题上,比如‘存在’。”

我要追问一个在我看来更为重要的问题:即使在变异逻辑中确实存在逻辑联结词的意义改变,为什么会发生逻辑联结词的这种意义改变呢?实际上,蒯因本人部分地(在我看来,正确地)回答了这个问题:“在拒斥排中律时,他实际上是
抛弃了经典否定或析取
,
或是两者都抛弃了
;
他可能有他的理由
。”
 “尝试我们所想做的,三值逻辑却原来是忠实于形式的:
它是对经典的真假二分法或经典否定的拒斥
。”
“尝试我们所想做的,三值逻辑却原来是忠实于形式的:
它是对经典的真假二分法或经典否定的拒斥
。”
 “直觉主义者不应被看成,在某些固定的逻辑算子即否定和析取的那些真的定律方面,与我们有争执。
他毋宁应该被看成是反对我们的否定和析取
,
认为是不科学的观念
,
而提出他自己的某种别的有些类似的观念
。”
“直觉主义者不应被看成,在某些固定的逻辑算子即否定和析取的那些真的定律方面,与我们有争执。
他毋宁应该被看成是反对我们的否定和析取
,
认为是不科学的观念
,
而提出他自己的某种别的有些类似的观念
。”

我想强调指出,变异逻辑学家与经典逻辑学家在重要问题上的分歧还可以追溯到更为根本的层次:关于逻辑与实在的关系、逻辑与认知和思维的关系,以及逻辑与数学的关系,他们持有很不相同的立场。例如,作为变异逻辑的直觉主义逻辑根植于一种非常独特的数学哲学——直觉主义。达米特正确地指出,直觉主义者“承认,他附加给数学词语的意义不同于经典数学家附加给它们的意义;但是,他坚持认为,经典的意义是不融贯的,出自经典数学家对数学语言如何起作用这一点的误解。于是,对‘如何可能去怀疑基本的逻辑规律’这个问题的回答就是:在有关逻辑的不一致的背后,还有更为根本的关于正确的意义模式的不一致,也就是关于我们应该把什么东西看作理解一个陈述的构成要素方面的不一致”
 。
。
4.用逻辑修正逻辑的悖论
在《依据约定为真》(1936)一文中,蒯因论述说,无论是逻辑的约定还是非逻辑的约定,都要符合于相关词项的日常用法;在证成我们所选择的约定时,我们不得不诉诸其他的约定,这将导致循环论证和无穷倒退:“……如果逻辑是从约定中产生的,那么,为了从约定中推出逻辑,也需要逻辑。”

达米特、哈克和博格西安都注意到了相同的现象:在证成最根本的逻辑规则时,例如肯定前件式和否定后件式,我们不得不使用那完全同样的规则,所以我们在进行某种循环论证,这似乎是“悖论性的”。

类似的情形也出现在蒯因的逻辑可修正性论题中:在修正逻辑时,我们不得不使用逻辑。这种情形似乎也是悖论性的,暂且称其为“用逻辑修正逻辑的悖论”。不过,我认为这个“悖论”不是真实的。我将诉诸蒯因最著名的隐喻——“纽拉特之船”来论证这一点:“纽拉特把科学比喻为一条船,如果我们想对其重建,我们必须在航行过程中一块甲板接着一块甲板地重建。哲学家和科学家在同一条船上。”
 下面,我用该隐喻去证成逻辑的可修正性而并不导致矛盾和循环论证。
下面,我用该隐喻去证成逻辑的可修正性而并不导致矛盾和循环论证。
(1)在修正逻辑(即经典逻辑)时,我们通常拒绝经典逻辑的一些规律,而接受经典逻辑的大多数其他规律。例如,直觉主义逻辑仅仅放弃了排中律、间接证明、双重否定律以及经典逻辑的相关规律;弗协调逻辑仅仅排除了矛盾律、爆炸律(即A∧¬A→B)以及经典逻辑的相关规律。在修正经典逻辑的某个部分时,可以使用我们仍然接受的经典逻辑的其他部分。这里根本没有什么矛盾或悖论。实际上,我们既不能拒绝经典逻辑的所有规律,也不能构造一个与经典逻辑完全不相同的新逻辑。
(2)即使我们用一种新的逻辑来修正经典逻辑,这种新逻辑与经典逻辑并不处于相同的层次。在这种情况下,经典逻辑是对象逻辑,而新逻辑是元逻辑。我们用元逻辑来评价或修正对象逻辑,然后用另一种新逻辑去证成第一种新逻辑。按照这种方式,我们没有任何明显的循环或悖论,但有某种无穷倒退论证。不过,并非任何无穷倒退论证都是恶性的,至少它们中的一些是合理的和可证成的,正如蒯因所言,在证成整个科学时,我们没有最后的立足点。
(3)逻辑可修正性论题仅仅意味着:若有必要,我们可以修正逻辑;它并不意味着:我们在某些情形下必须修正逻辑。换言之,修正逻辑只是一种可能性,而不是必然性。我们还要清楚地意识到:修正逻辑是代价最大的选择,我们必须慎之又慎;在考虑选择去修正经典逻辑时,我们必须依据翔实的分析和深入的思考,必须有足够充分的理由。
为什么逻辑是可修正的?逻辑与我们生活于其中的世界、与我们关于这个世界的认知、与我们的语言实践有联系吗?如果有联系,如何联系?如果逻辑确实是可修正的,我们如何修正逻辑?更具体地说,我们通过什么样的方式、程序或手段来修正逻辑?为什么对于大多数人来说,甚至对于某些资深哲学家来说,接受逻辑的可修正性论题显得如此困难?等等。对于这些问题,蒯因的整体论只为我们勾勒出一幅非常粗略的图画;他没有为我们提供更为翔实的解释和合理的论证。如果他还活着,他应该进一步处理这些问题,并且给出一个足够成熟的说明。然而遗憾的是,他不能再做这些事情了。所有这些工作都留待我们去完成。
在我看来,所有这些问题都可以还原为一个带有根本性和实质性的问题:我们需要对逻辑及其可修正性做全面的证成吗?我的回答是:当然需要!因为逻辑处于我们知识体系的基础和中心,如果它出错了,这将给我们的知识体系带来危险,甚至造成这个体系的崩溃。如果我们要清楚正确地理解我们的自然知识的本性,我们就不得不首先清楚正确地理解我们的逻辑知识的本性。下面,我将遵循蒯因的自然化认识论的精神,发展出对逻辑及其可修正性的系统性证成,其中包括实在论证成和认识论证成。
我的基本观点是:逻辑与我们生活于其中的世界、与我们关于这个世界的认知以及与我们的语言和思维实践有关联。明确地说,逻辑理论包含关于世界、认知、语言和思维的描述性内容或事实性因素。描述对于被描述者而言可真可假,逻辑理论也有可能出错,这就是为什么逻辑是可修正的根本原因。

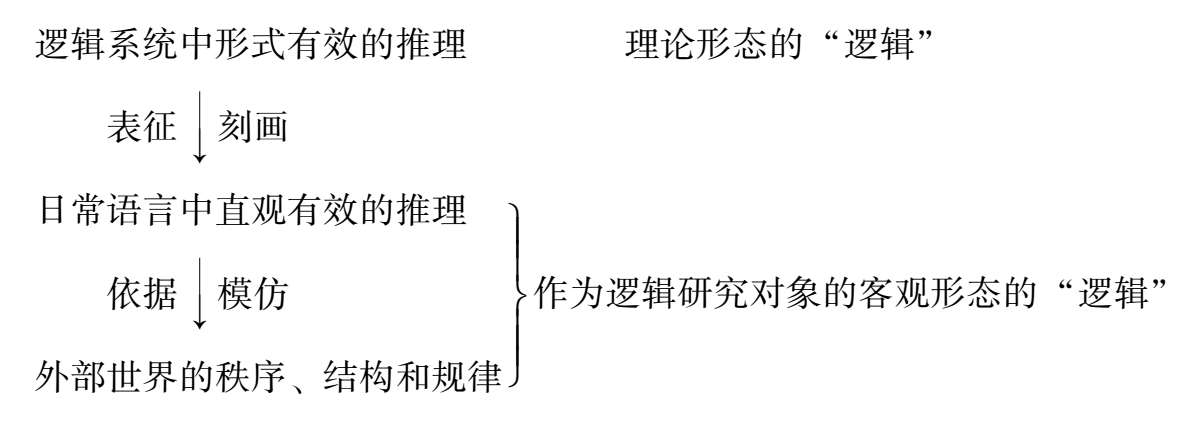
作为预备性工作,我想强调“客观逻辑”(objective logic)与“理论逻辑”(theoretical logic)之间的区别。“客观逻辑”是一种广义上的存在逻辑,即作为外部世界的秩序、结构和规律而存在的逻辑,人们在其日常生活中遵循这种逻辑,去指导和规范他们如何思考和行动。“理论逻辑”则体现为逻辑学家们所构建的逻辑系统,它们是对客观逻辑的描述、刻画和重构,因而不是被发明而是被发现的,所以可真可假。我提出如下的逻辑研究模型:
1.逻辑及其可修正性的实在论证成
我认为,逻辑深深地根植于我们的认知方式、思维方式和语言使用方式之中,所有这些都最终建基于外部世界的秩序、结构和规律。因此,逻辑与外部世界具有直接或间接的联系。如果逻辑在这个世界中起作用,它必须以这个世界为基础,然后从世界那里获得合作。对于上述观点,我给出如下五个从弱到强的理由。
(1)非常基本的逻辑规律同时也是存在的规律、认知的规律和语义的规律,例如矛盾律和排中律。亚里士多德在《形而上学》
 中已经论证过这一点。
中已经论证过这一点。
第一,亚里士多德断言,矛盾律和排中律是事物的规律和存在的规律。“……事物不能同时既是又不是。”(996 b 29-30)“同一属性不能在同一时间且在同一方面既属于又不属于同一对象。”(1005 b 18-20)“我们现在已经设定,任何事物不可能同时既是又不是,由此也已经表明,这是所有原则中最不可争议的。”(1006 b 3)“同一事物不能在同一时间既是又不是。”(1061 b 34- 1062 a 1)
第二,亚里士多德宣称,这两个规律是我们的认知行为(例如知道、相信、肯定和否定)的指导原则。“任何人不可能相信同一事物既是又不是。”(1005 b 23-24)“同一个人不可能同时相信同一事物既是又不是。”(1005 b 28-30)“对立之间没有居中地带,但我们对于一个主词必须或者肯定或者否定一个谓述。”(1012 b 11-13)“不可能同时真正地肯定和否定。”(1011 b 20)“所以不可能对同一主词真正地做出相对立的肯定和否定。”(1062 a 23-24)
第三,亚里士多德认为,这两个规律是支配语句或陈述真假的语义学规律。“对立陈述不同时为真”;“对立的东西对于同一事物同时为真,这是不可能的”(1011 b 13-16)。“不能对同一主词同时做出对立的陈述,也不能做出相反的陈述”(1063 b 15-18)。“对于任何东西,或者肯定是真的或者否定是真的。”(143 b 15)我们由矛盾律和排中律得到二值原则:任何语句、命题或陈述必须或者是真的或者是假的,它们有且仅有一个真值:真或假。矛盾律、排中律和二值原则共同刻画或确定了亚里士多德的真概念:“说是者为非或非者为是,这是假的,而说是者为是或非者为非,这是真的;因此,说任何东西是或不是,将或者说真的或者说假的。”(1011 b 25- 26)
更为重要的是,亚里士多德表明,矛盾律和排中律作为存在规律可以解释它们作为认知和语义规律的地位,前者决定后者。“……如果对立的性质不可能同时属于同一对象……显然,同一个人也不可能同时相信同一事物既是又不是。”(1005 b 26-31)也就是说,事物如何存在决定了我们应该如何认识和思考。矛盾律和排中律首先是作为存在的规律,然后派生出它们作为认知和语义的规律。
(2)经典逻辑不是本体论中立的,它有自己的本体论承诺。
经典逻辑在本体论上并不是完全中立的,它有许多定理对外部世界或经典逻辑的论域做出了存在性断言,例如,∃x(x=x)、¬∃x(Fx∧¬Fx)和∃x(Fx∨¬Fx),其中“∃x(x=x)”是说某物存在。经典逻辑还有两个关于论域的假定:(i)其论域必须是非空的,即是说,经典逻辑的量词毫无例外地有存在涵义,经典逻辑的所有单称词项都指称该论域中的个体,故经典逻辑中不存在无指称的词项。否则,对于一个含无所指词项的句子,我们将无法确定其真值,二值原则将不成立,还会导出一些很不自然的结果。(ii)其论域也不能太大,例如,既不能存在绝对无穷的个体,也不能包含所有集合的集合。否则,经典逻辑将会产生一些悖论。

(3)逻辑理论依赖于我们如何对外部世界进行概念化。
亚里士多德引入了十个范畴:实体、数量、性质、关系、地点、时间、状态、具有、主动和被动。实体范畴是所有其他九个范畴的核心,它们都从不同角度规定和说明了实体范畴,都可以归属于“属性”范畴。实体是所有属性的承担者,可以用作语句的主词。相反,所有其他范畴仅可以用作语句的谓词。因此,亚里士多德十范畴系统的一个逻辑后果是对语句做主谓式分析,在此基础上他发展出关于直言语句、直接推理和三段论的理论,这是人类历史上最早的逻辑系统。这种逻辑给出了如下的世界图景:世界由第一实体(个体)和第二实体(种和属)构成,实体具有其他九个范畴所刻画的属性或性质,例如可感的、在时空之中等等。
康德引入了范畴表和判断表。他的范畴表有四组,其中每组又有三种范畴:(1)量:统一性、多样性和总体性;(2)质:实在、否定和限制;(3)关系:实体和偶性、原因和结果、主动和被动之间的交互作用;(4)模态:可能和不可能、存在和不存在、必然和偶然。他的判断表也有四组,每组又有三种判断:(1)量:全称、特称和单称;(2)质:肯定、否定和无限;(3)关系:直言、假言和选言;(4)样式:或然、实然和必然。康德给出了比亚里士多德更为丰富的内容,也描绘了一幅更为复杂的世界图景:世界由对象和对象的类构成,它们不仅具有特定性质,而且处于复杂的相互关系中,其中最重要的关系是因果关系。但是,康德并没有摆脱对语句做主谓式分析的藩篱,只是增加了基于因果关系的语句之间的条件关系(由“如果,则”表达),以及“可能”和“必然”这些模态性质。19世纪之前的传统逻辑就是建立在康德对世界的概念化基础上的。
弗雷格用他对语句的主目函数分析取代了亚里士多德对语句的主词-谓词分析。在数学中,函数有空位(自变元或主目),是不饱和的,需要填充;填充并经过适当运算后就得到一个应变元。弗雷格从不同方面扩展了函数的概念,例如,自变元和定义域、函数的运算,以及应变元和值域,并且提出了如下的重要主张:概念是从对象到真值的函数。如果概念有一个空位,如F(x),它是一元概念;如果概念有两个空位,像R(x,y),它是二元概念;以此类推。这类语句是原子的,由此通过逻辑联结词和量词可以构造复合语句。最后,我们得到真值函项和带等词的量化逻辑。弗雷格的分析为我们提供了关于外部世界的另一幅图景:世界由个体或个体的类构成,其中的个体不仅具有特定属性或性质,还处于复杂的相互关系之中……
(4)逻辑是自然的教导,它对人类来说甚至具有生存价值。
蒯因曾用达尔文的自然选择理论说明了物种的相似标准、预期的成功以及归纳的效率。他谈道,“达尔文给了我们某种鼓舞。假如人们的性质划分是与基因有关的特性,那么已经导致最成功归纳的划分将会倾向于在自然选择中占据主导地位。在其归纳过程中犯错误的生物有一种可怜却值得赞扬的倾向:在繁衍其种类之前就已经死去”
 ,“我感谢归纳的有效,并且注意到,如果达尔文的进化论是真的,那么它有助于解释哪种归纳是灵验的”,“学习能力本身是具有生存价值的自然选择的产物”
,“我感谢归纳的有效,并且注意到,如果达尔文的进化论是真的,那么它有助于解释哪种归纳是灵验的”,“学习能力本身是具有生存价值的自然选择的产物”
 。
。
我同意蒯因的说法,并且想把他对归纳的说明扩展到对演绎逻辑效力的解释中。实际上,语言和逻辑都是人类为了满足他们的生存需要而回应外部世界以及相互合作的手段。正是自然界本身以及从中获取生存经验的老一代人教会新一代人如何思考和行动。世界对我们正确的思想和行为给予成功的奖赏,对我们的错误思想和行为给予失败的惩罚。日积月累,我们不断积累正确的思维方式,并且将它们内化为我们的认知和行为的普遍结构,这就是客观形态的逻辑,也就是逻辑学家试图在他们的研究中发现和刻画的对象。
因此,我们的逻辑(即经典逻辑)在外部世界中有事实基础。有些逻辑真理不仅是语义有效的,而且是事实真的。举例说明。∀x(x=x)是说,所有事物都是自身同一的;¬∃x(F(x)∧¬F(x))是说,世界上没有任何事物具有某个性质同时又不具有这个性质;所谓“莱布尼茨律”,即∀x∀y((x=y)→(F(x)→F(y)))是说,如果两个事物是同一的,即它们是相同的事物,那么,如果其中之一具有某个性质,则另一个也具有该性质,反之亦然。所有这些公式都是事实真的,因为它们报道了世界的实际情况,世界的事物正如这些公式所说。另外,有些推理形式,例如肯定前件式(p→q,p┣q)和三段论(如MAP,SAM┣SAP),表达了世界的自然秩序以及事物的真实关系,所以它们是关于世界的事实真理。如果遵循它们去思考和行动,我们就有可能获得成功。相反,有些公式,例如∀x(x¹x)、∃x(F(x)∧¬F(x))以及所谓的“莱布尼茨怪律”,即∀x∀y((x¹y)→(F(x)→¬F(y))),既不是语义有效的,也不是事实真的。例如,莱布尼茨怪律说:如果两个事物不同一,那么,如果其中一个具有某性质,则另一个必定不具有该性质。这等于预设了下面一点:世界中任何两个不同的事物都具有完全不同的性质;换言之,相同的性质不能被世界中不同的对象所分享。这个主张是事实假的:这是关于世界的一个荒谬假定。另外,有些推理形式,例如肯定后件式(p→q,q┣p)和三段论(如PAM,SAM┣SAP)错误地表达了世界的自然秩序和事物之间的关系,所以它们不是事实真的。如果我们遵循它们去思考和行动,我们最终会失败,自然界会惩罚我们的错误思考。
谢尔(Gila Sher)正确地断言:“在某种程度上,使用其他错误理论会导致飞机失事、工人失薪、核电站关闭(或爆炸)、汽车熄火(或相撞)等等,所以,使用错误的逻辑理论也会导致这些情况。的确,科学实在论者对科学理论(或这些理论的抽象部分)所说的也适用于逻辑理论:如果逻辑理论不与世界一致,那么,它在世界中的作用将会变得神秘莫测。
因此
,
在设计一个逻辑系统时
,
必须将世界考虑在内
。”

(5)逻辑通过真谓词指向世界。
蒯因认为,虽然逻辑必须诉诸语义上溯,但它与实在有关:在把真谓词归属于语句的同时,也把这个谓词以间接的方式归属于实在。“在这里,真谓词如实地能用来通过语句指向实在;它能用作提醒者,提示我们,虽然提到语句,但实在仍然是全部的关键”,“逻辑理论虽然严重依赖于语言的谈论,但已经是朝向世界而非朝向语言了,真谓词使之如此”
 。
。
谢尔把这个想法发展为对逻辑的一个很系统的基础性解释,其中包含了对逻辑的实在论说明。她将其称为“基础整体论”(foundational holism)。我认为,她的理论在总体上是正确的,与我先前的想法不谋而合。
 下面我用自己的话概述谢尔的论证。
下面我用自己的话概述谢尔的论证。
众所周知,逻辑是研究推理和论证的,特别是它们的形式有效性。逻辑后承(logical consequence)是逻辑的核心概念。可以用两种不同的方式来刻画它:语法(或证明论)和语义(或模型论)。我偏向于语义刻画。对逻辑后承的塔斯基式标准定义是:
语句α是语句集Γ的后承一,当且仅当,不存在个模型使得Γ的所有语句是真的而α是假的。用符号表示:
Γㅑ L α
这里,“L”指任一逻辑系统,我们也可以称其为一个逻辑。
为简单起见,我们只考虑两个语句S 1 和S 2 之间的推理关系:
S 1 ㅑ L S 2
根据塔斯基式定义,逻辑后承的最重要特征是:无论推理的链条多长,从推理的前提到结论保持真或传递真。因为涉及语句或语句集的真,世界必须参与,用谢尔的话说,“世界必须合作”
 。一个语句是真的,仅当世界的相关事物如同这个语句所说;一个语句集是真的,仅当该集合的任何一个语句都是真的,即仅当世界的相关事物如同这些语句逐个所说。另外,由于后承关系是语句的真的传递或保持关系,故在处理后承关系时,我们必须考虑事物所是的诸方式(相对于相关语句)之间的联系(或缺少联系),也就是说,语句集G是语句a的后承,当且仅当,存在语句集G所说的事物与语句a所说的事物之间的联系。我们由此得到谢尔的如下图示:
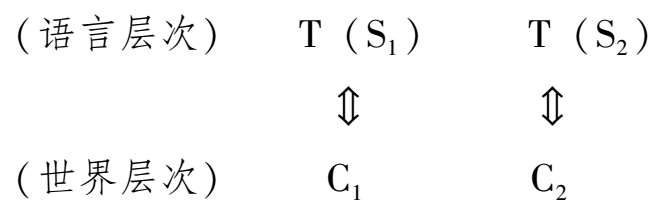
。一个语句是真的,仅当世界的相关事物如同这个语句所说;一个语句集是真的,仅当该集合的任何一个语句都是真的,即仅当世界的相关事物如同这些语句逐个所说。另外,由于后承关系是语句的真的传递或保持关系,故在处理后承关系时,我们必须考虑事物所是的诸方式(相对于相关语句)之间的联系(或缺少联系),也就是说,语句集G是语句a的后承,当且仅当,存在语句集G所说的事物与语句a所说的事物之间的联系。我们由此得到谢尔的如下图示:
(逻辑层次)S 1 ㅑ L S 2
假定S 1 是真的。为了让(3)是真的,S 1 的真必须保证S 2 的真,即如下情况必须成立:
(语言层次)T(S 1 )→T(S 2 )
令C1和C2是让这两个语句为真而在世界中所要求成立的条件(情形):
谢尔继续论证,实在对逻辑有两种方式的影响。一种方式是“逻辑被世界所限制,即世界至少对逻辑具有负面影响”
 。如果我们同时发现世界的两个情形C1和非
C
2,这就确定了T(S
1
)而非T(S
2
),这个发现将直接让逻辑后承“S
1
ㅑ
L
S
2
”无效。另外,如果我们发现:世界的情形C1出现无论如何不能保证情形C2出现,这个发现就意味着,T(S
1
)不能保证T(S
2
),所以这也使逻辑后承“S
1
ㅑ
L
S
2
”无效。
。如果我们同时发现世界的两个情形C1和非
C
2,这就确定了T(S
1
)而非T(S
2
),这个发现将直接让逻辑后承“S
1
ㅑ
L
S
2
”无效。另外,如果我们发现:世界的情形C1出现无论如何不能保证情形C2出现,这个发现就意味着,T(S
1
)不能保证T(S
2
),所以这也使逻辑后承“S
1
ㅑ
L
S
2
”无效。
另一种方式是
世界使逻辑成为可能
(logic is also enabled by the world),这意味着“世界或许使得从一些语句
逻辑地得到
其他语句(假如给定某些东西,如语言和意义)”
 。例如,假定世界被如下很可能是必然且普遍的规律所支配:
。例如,假定世界被如下很可能是必然且普遍的规律所支配:
A∪(B∩C)非空⇒A∪B非空
这个规律足以支持如下断言:
∃x(Ax∨(Bx&Cx))ㅑ L ∃x(Ax∨Bx)
我同意谢尔的如下总结:“理论上,逻辑通过如下方式根植于实在:(i)它与真的内在联系,(ii)真与实在的内在联系,以及(iii)从(ii)到(i)的内在相关性。而且逻辑根植于支配世界的特定规律,这些规律具有极强的模态力量……”

2.逻辑及其可修正性的认识论证成
蒯因主张,“我们在学习语言的过程中学习逻辑”
 。他认为:“因此,从‘p并且q’到‘p’推理的逻辑规律正是通过对‘并且’的学习成为我们的习惯。对于合取的其他规律以及析取和其他真值函项的规律也是类似的。相应地,对于量化的规律也类似……因此
,对我们的基本逻辑习惯的习得可以用我们对语法构造的习得来解释
。”
。他认为:“因此,从‘p并且q’到‘p’推理的逻辑规律正是通过对‘并且’的学习成为我们的习惯。对于合取的其他规律以及析取和其他真值函项的规律也是类似的。相应地,对于量化的规律也类似……因此
,对我们的基本逻辑习惯的习得可以用我们对语法构造的习得来解释
。”
 “归纳本身与动物的期望和习惯的形成在本质上是相同的,只不过有程度的差别。语词的实指学习是归纳的一个隐含例子。”
“归纳本身与动物的期望和习惯的形成在本质上是相同的,只不过有程度的差别。语词的实指学习是归纳的一个隐含例子。”

我同意蒯因的观点:我们在学习语言的过程中学习逻辑,但是语言的学习过程实际上是一个归纳过程,至少是与归纳有关的。从这些前提出发,我们可以推出逻辑的学习过程也与归纳有关这个结论吗?我认为是如此的。客观逻辑根植于我们的语言和认知实践中,也根植于我们的思维方式中。理论逻辑是对客观逻辑进行表述、抽象和理想化的结果。
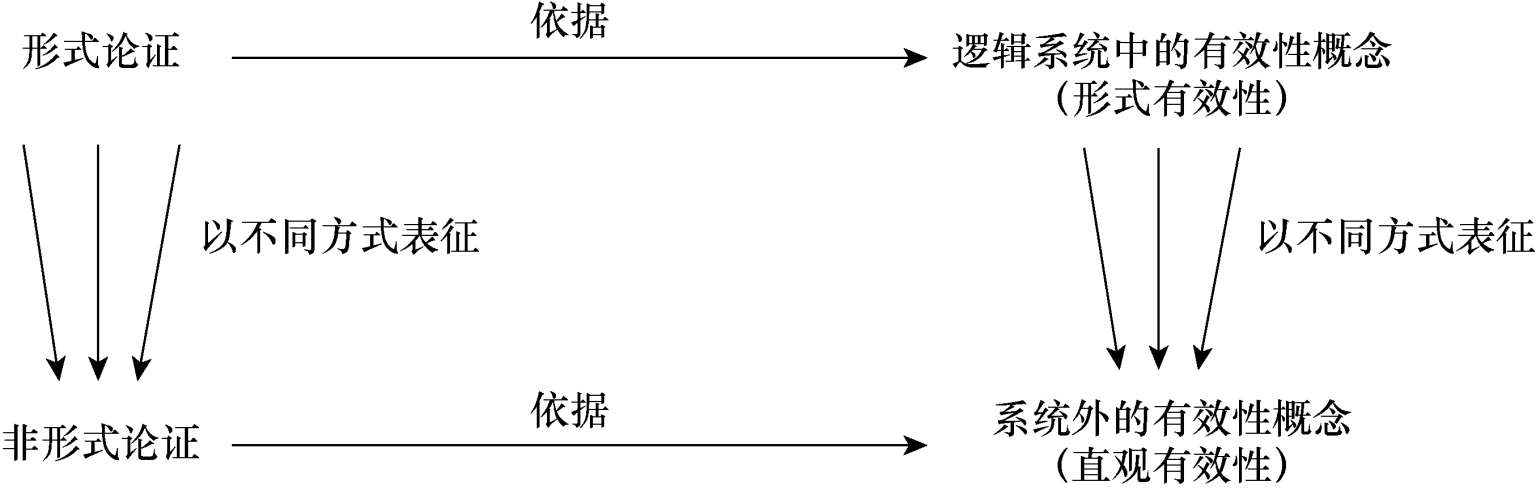
通常,逻辑学家把用自然语言表述的我们日常思维中的推理重新表述为用形式语言表述的逻辑系统中的推理。日常语言中的推理可被称为“非形式论证”,逻辑系统中的推理被称为“形式论证”。前者依赖于系统外的有效性这个概念,亦称“直观有效性”;后者依赖于逻辑系统中的有效性这个概念,亦称“形式有效性”。哈克指出:“形式逻辑系统试图对非形式论证进行形式化,试图用精确、严格和一般化的词项来表达它们;而一个可接受的形式逻辑系统应该是这样的,如果一个给定的非形式论证通过某种形式论证在其中得到表达,那么,只有非形式论证在系统外的意义上是有效的,形式论证才应该在系统中是有效的。”

当然,在这一过程中,我们会遇到许多模糊和含混,不同的逻辑学家对非形式论证及其直观有效性将做出不同的理解和解释,对此构造出不同的甚至相互排斥的逻辑系统。因此,一个普遍的现象是:不同的逻辑或逻辑系统同时并存。这种观点被称为“逻辑多元论”,图示如下:
在这一过程中,逻辑学家必须对我们的认知和语言实践进行某种经验研究,包括我们形成概念、做出判断、进行推理、论证和反驳的方式和方法。不过,逻辑学家既不关心推理的具体心理过程,也不关心推理前提和结论的实际真值,而是专注于如下问题:通过何种规则、程序和方式,从真前提可以推出真结论。因此,逻辑学家的工作不同于心理学家的工作,至少是研究侧重点有所不同。
总之,像在其他科学中一样,在逻辑系统中也存在对我们认知和语言实践的描述、刻画、提炼、精释、抽象、概括和理想化。逻辑理论需要得到关于自然语言和日常思维的直观的支持,并且与关于世界、认知和语言用法的经验材料有关联。
我的上述逻辑观近似于麦迪(P·Maddy)的自然主义逻辑观,后者包括三个论题:
(1)人类是如此构造的,以至于他们使用康德/弗雷格的形式和范畴对这个世界做概念化,也由于这个原因,他们的思考要受到逻辑规律的约束,但现代逻辑的全部规律要等到某些重要的理想化处理和补充假设出现之后才会产生出来。(2)在很大程度上,这个世界具有与这些形式和范畴相对应的一般性的结构特征,但也有例外的情况,在那里即使是那种基础的逻辑也会失去其基础。(3)人们之所以相信逻辑的基础部分,是因为它们由其基本概念装置所决定,但他们得知那些规律,也只是因为那些基本的概念化处理可以被证明是真实的。

不难理解,蒯因的逻辑可修正论题可以得到这种逻辑观的强有力的支持。
3.我们如何修正逻辑?如何构建和评价一个新逻辑?
因为修正经典逻辑总是导致建构一种“新”逻辑,所以我把上面两个问题合而为一:构建一个逻辑系统的程序以及评价该系统的标准是什么?
在我看来,逻辑学家与其他领域的科学家没有本质性区别。他们都必须使用假说演绎法:先发现问题,确立研究目标;搜集经验材料,为以后的理论化做准备;构造尝试性假说;根据各种标准,对这个假说进行评价;从该假说推出许多结论或预测,通过实践或推测进行检验;不断改进这个理论,直到得到广泛认可和应用。许多逻辑学家不这样认为,只是因为他们各自只做了构建逻辑系统这个整体任务中的部分工作,逻辑学家共同体不得不完成所有其他的工作,包括对所构建的逻辑系统做评价、选择和使用。

(1)发现问题,确立研究目标。
例如,对于莱布尼茨来说,他想发明一套普遍语言和理性演算,把所有的推理都化归为计算,由此达到思维的程序性、严格性和精确性。他一生不断尝试实现这一目标。又如,对于弗雷格来说,他想把数学化归为逻辑,由此证明数学的一致性和可靠性。但当时已有的逻辑不能用来实现这个目标,所以他竭尽全力创造一种新逻辑。当代计算机科学和人工智能提出了许多经典逻辑不能满足的新要求,故逻辑学家们正在构造各种新的逻辑系统,例如认知逻辑,关于行动、博弈和决策的逻辑,关于自然语言表征和理解的逻辑。
(2)进行预备性的经验考察。
在建构新逻辑系统之前,逻辑学家必须对相关领域有足够的理解。例如,他们应该澄清相关领域中重要的概念和命题,消除它们的歧义和不精确性,清楚地理解那些概念和命题之间的实际逻辑关系,从而确定哪些概念和命题是基本的,哪些概念是可定义的,哪些命题是派生的。例如,在构造时态逻辑、道义逻辑、认知逻辑时,逻辑学家必须先进行有关时间、义务和规范以及知识的哲学研究,从而为以后的形式化工作奠定实证基础。
(3)构造新的形式系统。
这是逻辑学家的本职工作,也是构造逻辑系统的关键步骤。具体工作包括:先设计一个形式语言,然后选择演绎装置的集合,其中包括目标系统的公理和推理规则,最后从这个系统的演绎装置集合中推出许多定理,由此构成一个形式化系统。
(4)对形式系统的元逻辑证成。
并非任何构造出来的形式系统都有资格被看作逻辑。合格的系统必须具有一些元逻辑特征,例如可靠性、一致性、完全性、独立性、可判定性、范畴性等等。其中最重要的是形式系统的可靠性,它关系到一个形式系统是否成立的问题,即该系统的所有定理是否都是逻辑真的。不可靠的形式系统可以推出矛盾,而推出的矛盾足以摧毁那个系统。系统的完全性也是非常重要的,因为它与系统的推演能力有关,即是否所有逻辑真理都可以作为该系统的定理推演出来。既可靠又完全的形式系统一直是逻辑学家们所追求的目标。
然而,形式系统的可靠性和完全性却不能充分证成一个逻辑系统,可以给出两个理由:(i)相互冲突的逻辑系统可以分别是可靠的和完全的;(ii)在各种可靠和完全的系统中,有的得到广泛认可和应用,有的则被忽视甚至被完全遗忘。发生此种现象必定另有原因。
(5)对形式系统的认识论证成。
既然逻辑系统是对于我们的语言和认知实践的抽象化和理想化,并且与外部世界有关,因此,还必须给出系统的认识论证成。我们应该考虑,系统是否对应于我们的认知、思维和语言使用,是否与我们在相关领域的直观和常识相冲突,等等。
夏皮罗(S·Shapiro)指出,模型论和证明论都给出了逻辑后承的概念:前者通过解释或模型来说明后承,后者通过推理规则来说明后承。可靠性和完全性是关于形式系统的数学概念,它们仅是证成系统的必要条件。除此之外,演绎后承概念和模型论后承概念都预设了直观的和前理论化的后承概念,即自然语言中正确推理的概念。在某种意义上说,演绎后承概念和模型论后承概念是对自然语言中正确推理概念的刻画和描述,因此有如下问题:这些刻画或描述是否正确和充分?一个模型论语义学是正确的,如果它有足够的解释去拒绝任何混合意义上非有效的论证;一个模型论语义学是充分的,如果任何自然语言中混合意义上有效的论证都对应于一个模型论后承。类似地,一个演绎系统是正确的,如果它的任何初始推理规则都对应于一个合法的且没有间隙的推理步骤;一个演绎系统是充分的,如果任何自然语言中合法且没有间隙的推理链条都被重新纳入这个系统中。

(6)对形式系统的实用性证成。
在已经构建成功的逻辑系统中,我们的学术共同体进行选择的一个重要标准是:这些系统是否具有重要的理论和实践价值,是否有助于解决困难问题,是否得到普遍且有效的运用,以及是否简单和方便,等等。在开始阶段,一个逻辑理论不可避免地是幼稚和肤浅的,其理论和实践的价值常常不太高,例如,道义逻辑、认知逻辑、偏好逻辑等曾经处于这种情形中。不过,这种现象是很自然的,也会不断得到改进。世界中绝大多数人都是功利主义者,他们对没有价值或价值很小的东西没有耐心。然而,我想强调的是,请更耐心地对待逻辑的发现和创造,以长焦距、广镜头从不同侧面去评价一个逻辑系统。
4.为什么逻辑可修正性论题如此难以被认同?
下面讨论一个心理学问题,但其实也是一个认识论问题:对于大多数人来说,甚至对于某些资深哲学家来说,接受蒯因的逻辑可修正性论题为什么显得如此困难?我至少可以给出如下三个理由:
(1)逻辑与外部世界以及我们的认知的联系是如此之遥远和间接,以至于人们错误地认为没有这种联系。我想问一些很重要的问题:如果逻辑只是对世界无所言说的重言式,为什么它们可被运用于世界甚至在世界中管用?如果实际上不存在逻辑真理与人类思维实践之间的联系,为什么逻辑规律和规则对我们的思维具有支配性力量?在我看来,逻辑学家不应该构造这样的逻辑系统,即它们与我们的常识和语言直观有根本性冲突,且在我们的思维中毫无应用;即使他们这样做了,他们所构造的“逻辑”系统也不值得认真对待。如果不承认逻辑与人类经验之间有直接或间接的联系,逻辑真理的有效性对于人类认知来说将是难以理喻的谜团。实际上,并不是我们把自己的认知模式强加于世界,而是世界教导我们学习和遵循这些模式。人类在与世界打交道的过程中代代相传的积累的模式对于个别人来说是先天的,但是对于整个人类来说却并非如此,因为通过最终的分析,这些模式都具有实在论或经验论的起源。
(2)逻辑处于人类知识体系的中心地位。面对顽强不屈的经验,如果选择修改逻辑,我们将付出沉重代价。有些人由此再走一步,得出了逻辑不可修正的结论。但是,这个结论是错误的,因为逻辑真理在人类知识体系中的中心性并不等同于它的分析性、必然性和先天性,难以修正逻辑并不等同于逻辑可免于修正。的确,修正逻辑将导致巨大的改变,甚至导致世代积累的知识体系崩溃。这仅仅说明我们不能轻易修改逻辑,而并未证明我们不能修改逻辑。人类知识体系的巨大变化,即所谓的“科学革命”,在过去已经发生过多次,在未来很有可能还会发生。
(3)对逻辑可修正论的一种反对意见是:在修改逻辑时,我们也不得不使用逻辑,所以逻辑可修正性论似乎是自我否定的。我已在上面第二节回答了这个反驳。如我所论证的,经典逻辑的修正并不是全面的和整体的,而是部分的和局部的。因为经典逻辑按照某种方式反映和刻画了外部世界和我们关于世界的认知,它将被长期有效和普遍地使用,不是完全错误的,故不能被完全否弃。因此,在修正经典逻辑时,我们可以使用经典逻辑中我们仍然接受的那些部分。另外,有些逻辑学家用T2修正T1,其他逻辑学家用T3修正T2,更一般地说,另外一些逻辑学家用T n 修正T n-1 ,等等。我们必须一个接着一个地完成对经典逻辑的单个修正,就其本身而言,这些单个的修正是一致的和融贯的。因此,逻辑可修正性论并不是一个自毁的论题。
正如在日常生活层面,像休谟这样的怀疑论者与普通人没有什么区别一样,像我这样的逻辑修正论者与其他那些坚持逻辑不可修正的同行之间也没有实质性区别。虽然不承认逻辑真理具有绝对分析性、必然性和先天性,但我仍然认为,逻辑真理处于我们知识系统的中心,具有相对而言的分析性、必然性和先天性,所以,倘若修正逻辑,我们将付出巨大代价。我们行动的指导原则是蒯因的“最小损害原则”,所以我相信,虽然逻辑是可修正的,但我们不能任意地修正逻辑,我们必须具有非常强劲且充分的理由来这样做。对我们来说,不修正逻辑或许总是一个合理的策略和更好的选择。
