




你是否还记得初中的时候,老师让你做因式分解时的状况呢?
“为什么要做这种事啊?”我想很多人都会提出过这种疑问吧。
因式分解的目的当然不是为了折磨学生,其意义是增加式子的“信息量”。关于式子的信息量,我在《写给全人类的数学魔法书》中也有提及,去翻阅一下吧。
信息量会根据式子的形式发生改变。
式子的信息量

① A+B=0
② A×B=0
由式子①我们可知,
A+B=0
但是,相加得0的2个数字组合有无数个,比如1和-1、5和-5、10和-10……
也就是说,即使知道和为0,也无法确定A和B的数值。我们再看看式子②。
A×B=0
A×B的积为0,说明其中一个必定是0。即“A=0或B=0”。与①相比,②的信息量明显增加了。
与和相比,积的信息量更丰富,这就是进行因式分解的目的。
我在《写给全人类的数学魔法书中》介绍过的“与其考虑相加,不如考虑相乘”,就是“遇到任何数学题都能够解答的10种解题思路”之一。
在开始学习因式分解之前,让我们先总结一下多项式的计算吧。算式中的不同字母要区别对待。
5x+2y
举个例子,我们可以将上述式子简单地理解为5个苹果和2个橘子。
(5x+2y)+(x+3y)
我们可以把这个式子理解为,除了5个苹果和2个橘子外,又加了1个苹果和3个橘子。这时,我们就可以通过加法算出苹果和橘子的个数。
苹果:5+1=6(个)
橘子:2+3=5(个)
在此基础上,用代数式进行计算:
(5x+2y)+(x+3y)=(5+1)x+(2+3)y=6x+5y
字母相同(苹果、橘子)的项就被称为同类项。在多项式的加法运算中,同类项可以通过系数(字母前的数字)相加进行合并。
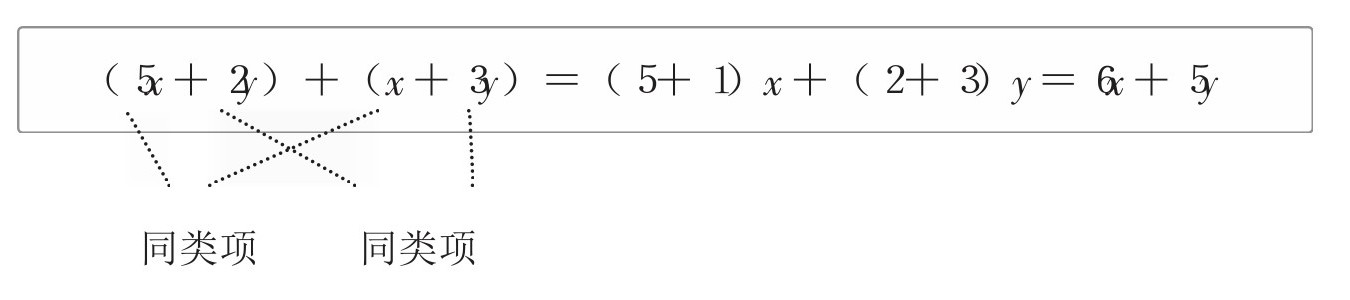
上面提到,只有同类项的系数可以进行加法运算,这根据的是下面的计算法则(分配法则)。
分配法则
(m+n)x=mx+nx
我们可以通过下面的图形,论证分配法则。
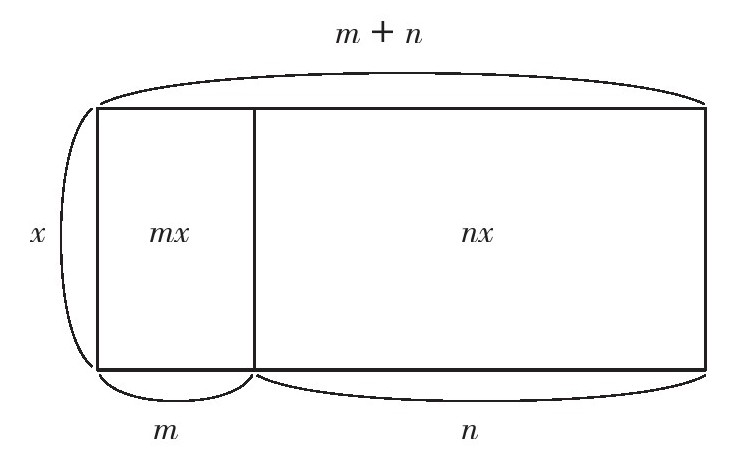
图中大长方形的面积是(m+n)x,该面积等于里面2个小长方形的面积mx和nx之和。
(m+n)x=mx+nx……①
所以上述等式是成立的。另外,A×B与B×A的结果相同,所以分配法则可以写成下面这种形式。
x(m+n)=mx+nx……②
如果A=B,那么B=A,所以分配法则也可以左右颠倒。
mx+nx=(m+n)x
下面的等式就是根据分配法则变形的。
5x+x=(5+1)x
2y+3y=(2+3)y
多项式×多项式也可以按照上述的分配法则进行计算。

多项式×多项式
(m+n)(x+y)=mx+my+nx+ny
该计算的正确性也可以通过下面的图形证实。
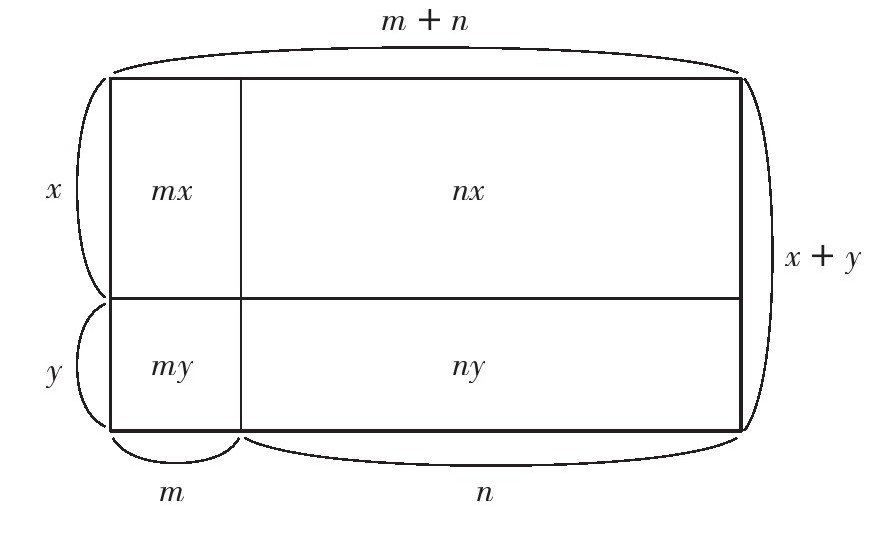
大长方形的面积=(m+n)(x+y)
4个小长方形的面积之和=mx+my+nx+ny
因为大长方形的面积等于4个小长方形的面积之和,
(m+n)(x+y)=mx+my+nx+ny
所以,上述计算是正确的。
我们今后会经常用到多项式×多项式,所以一定要反复练习,加以巩固。
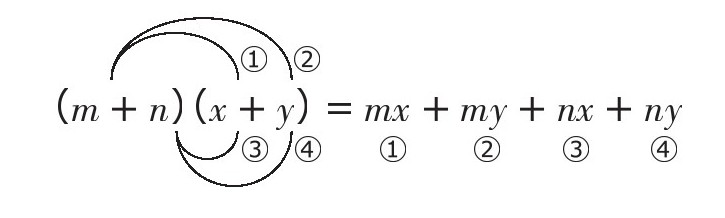
多项式×多项式的计算有多种形式,我整理出了下列公式。
乘法公式
(1)(x+a)(x+b)=x2+(a+b)x+ab
(2)(x+a)2=x2+2ax+a2
(3)(x-a)2=x2-2ax+a2
(4)(x-a)(x-a)=x2-a2
记住这些并不难,下面我们就用这些公式做几道练习题吧。我先把公式(1)~(4)的证明过程写出来,大家一定要多多练习,能独立用这些公式解题。
【证明】
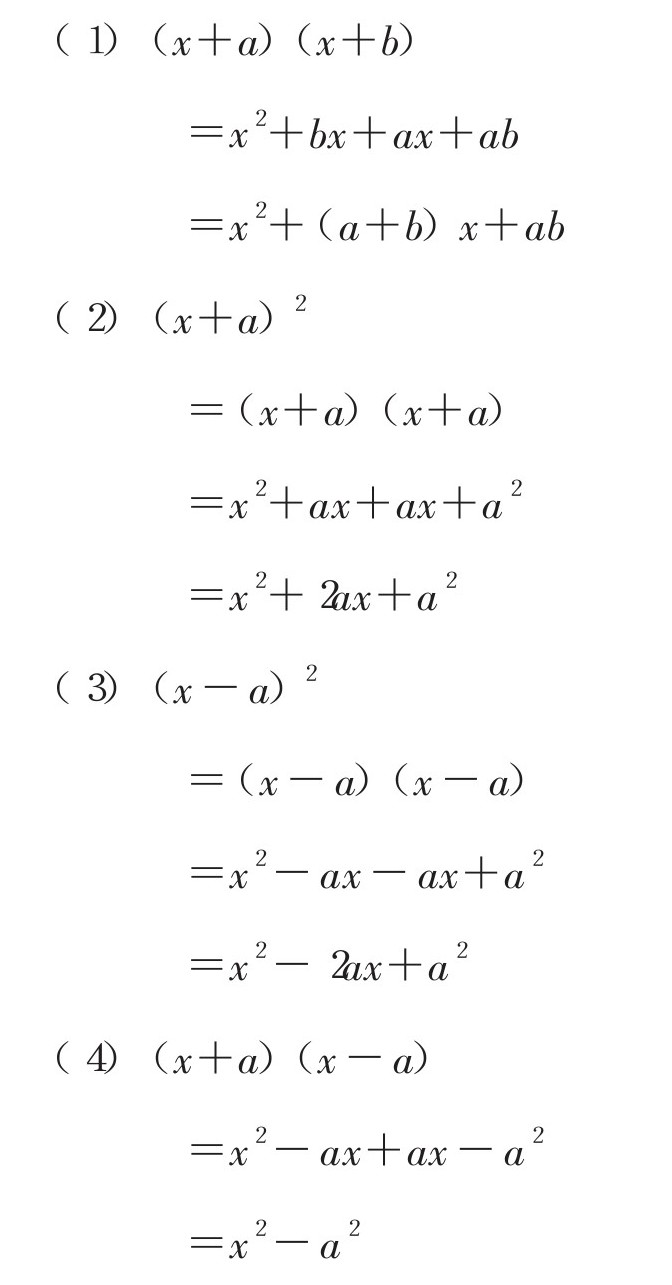
以上4个公式都很重要,其中最重要的是(4)。在公式(4)的证明中,(x+a)与(x-a)相乘后,-ax与+ax相互抵消,只剩下x2与-a2。对数学感兴趣的人,一定会惊叹“这个结果真神奇”,和与差这两个完全相反的概念相互抵消后,结果就变得简单明了了。或许你会觉得我的描述有些夸张,只要你亲自证明一下公式(4),也一定会发出这样的感慨:“哦哦!真的消掉了啊!”如果真是这样,你就发现了数学的乐趣和美妙。
接下来,我们就用公式(4)解一道应用题吧。
问题
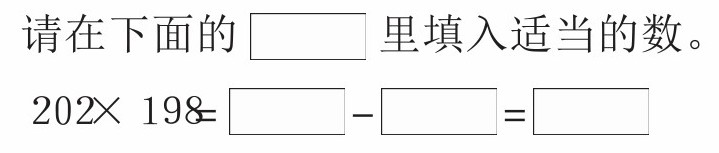
[明治学院高中部]
当然,你完全可以用笔算的方法得出202×198的答案,如果让你换种思路,也可以用公式(4)解开这个问题。
因为,
202=200+2
198=200-2
所以,
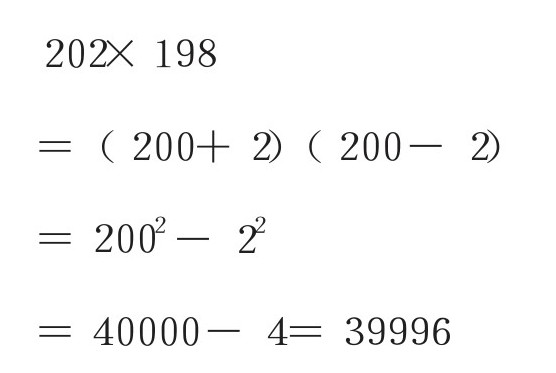
综上可见,①=40000,②=4,③=39996
因式分解的方法
多项式×多项式的式子变形成没有“()”的式子(分散),叫作“展开式”;反过来,将分散的式子变为多项式×多项式这种乘法运算形式,则叫作因式分解。
任何教科书上都会提到以下3条因式分解的基本要求。
因式分解的基本要求
①提取共同的因数
(例)ax+ay=a(x+y)
②对最低次的字母进行整理
③公式的利用
因式分解的公式
(1)x 2 +(a+b)x+ab=(x+a)(x+b)
(2)x 2 +2ax+a 2 =(x+a) 2
(3)x 2 -2ax+a 2 =(x-a) 2
(4)x 2 -a 2 =(x+a)(x-a)
因数分解与展开式相反,左右颠倒乘法公式,就是因式分解的公式。
在因式分解的基本要求中,第2条“对最低次的字母进行整理”最容易被学生遗忘。一小部分勤奋的学生虽然记住了这一条,却没有几个人能说明,为什么要对最低次的字母进行整理。
学习数学的目的是为了锻炼逻辑能力,解开未知的问题。会因式分解,却不能从中总结出能进行广范围应用的思考方法,就等同于学无所成。
因式分解是指,将算式改写成乘积的形式,换句话说,因式分解相当于式子的整理。
接下来的内容有点儿跑题,不过我还是希望大家能看看下面的照片。
书架上摆满了物理和化学的习题集,上面2层是物理习题,下面2层是化学习题。同一科目的书籍按照尺寸进行排列,同一尺寸的书籍按照出版社类别进行排列。

假设这个书架因为某些原因倒了,你会怎样整理散落一地的书呢?没错,首先按照科目类别分成物理和化学,然后按照尺寸大小排列,最后再按照出版社类别来排列。
从这个例子我们可以看出,整理事物时,最有效的方法是从变化较少的方面着手分类。再举个例子,如果想对面前的男女老少进行分类,那么最快的方法就是先按照男女类别来划分。
因式分解就是对式子的整理,所以也可以按照这种思路思考。
比如下面这个式子。
x 2 +xy-x-y
这个式子中,x是二次式,y是一次式。
(i)对x进行整理,式子就会分成3部分。
〇x 2 +△x+□
(ii)对y进行整理,式子只会分成2部分。
〇y+△
正如前面所说的,整理要从分类较少的方面着手。因此,对最低次的字母进行整理是最有效的方法。
x 2 +xy-x-y
不仅如此,对上面式子中的y进行整理后,还会得出下面的式子:
(x-1)y+x 2 -x
如果这个式子能进行因式分解,那么(x-1)或y都要加上括号。后半部分的x 2 -x中没有y,所以自然而然地会在x 2 -x中寻找(x-1)。像这样对最低次的字母进行整理,我们能从中得到一些启示,进而从式子中找到因式分解的出路,最后只要继续因式分解便能得出答案。
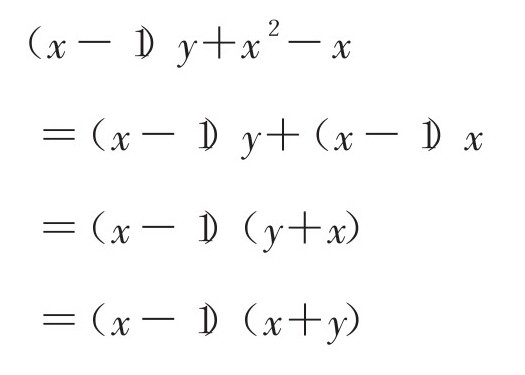
要想熟练地完成因式分解,实践练习必不可少,让我们来练习一下吧(不好意思,我在此直接用了高中的入学试题)!
问题
请对下列式子进行因式分解:
①x 2 y+5xy-14y [清风高等学校]
②3(x-3) 2 -48 [法政大学第二高等学校]
③a 2 b-b 2 c-b 3 +ca 2 [关西学院高中部]
【解答】
在①式所有的项中,共有的因数是y,所以先提出来。
x 2 y+5xy-14y=y(x 2 +5x-14)
接下来我们看括号里的内容。你看出括号里的式子是因式分解公式(1)的形式了吗?现在把公式和括号里的式子单独列出来。
x 2 +(a+b)x+ab=(x+a)(x+b)
x 2 +5x-14=?
综上所述,只要找到满足下述条件的a和b,就能完成因式分解。那么该如何处理呢?前面说过,积的信息量比和多,这里也是一样,积的式子包含了更多信息。
ab=-14
让我们来思考一下哪些a和b的组合能让该式子成立。在此,你可以限定a和b都为整数(非整数的例子到高中才会出现),因此,a和b的组合只有下列几个。
(a, b)=(1,-14)、(-1,14)、(2,-7)、(-2,7)
然后你再从中找出a+b等于5的组合,就只有唯一一个。
(a, b)=(-2,7)
综上可见,
x2+5x-14=(x-2)(x+7)
在面对下列候选组合时,
(a, b)=(-14,1)、(14,-1)、(-7,2)、(7,-2)
其实不用考虑正负颠倒的问题,因为
(x-2)(x+7)和(x+7)(x-2)
没什么区别。
在②式中先提取共有的因数3。
3(x-3) 2 -48=3{(x-3) 2 -16}
你发现了吗?16是个平方数(某个数平方后得到的数)。如果你发现了这个奥秘,就可以借助因式分解公式(4)进行解答。
(x-3) 2 -16=(x-3) 2 -4 2
为了方便大家套用,我在此把因式分解公式(4)也列出来。
x 2 -a 2 =(x+a)(x-a)
(x-3) 2 -16=?
利用这个公式,我们就能进行因式分解了,而解题的重点是将(x-3)看成一个整体。为方便起见,我在此用一个新的字母将其替换——假设(x-3)=X。
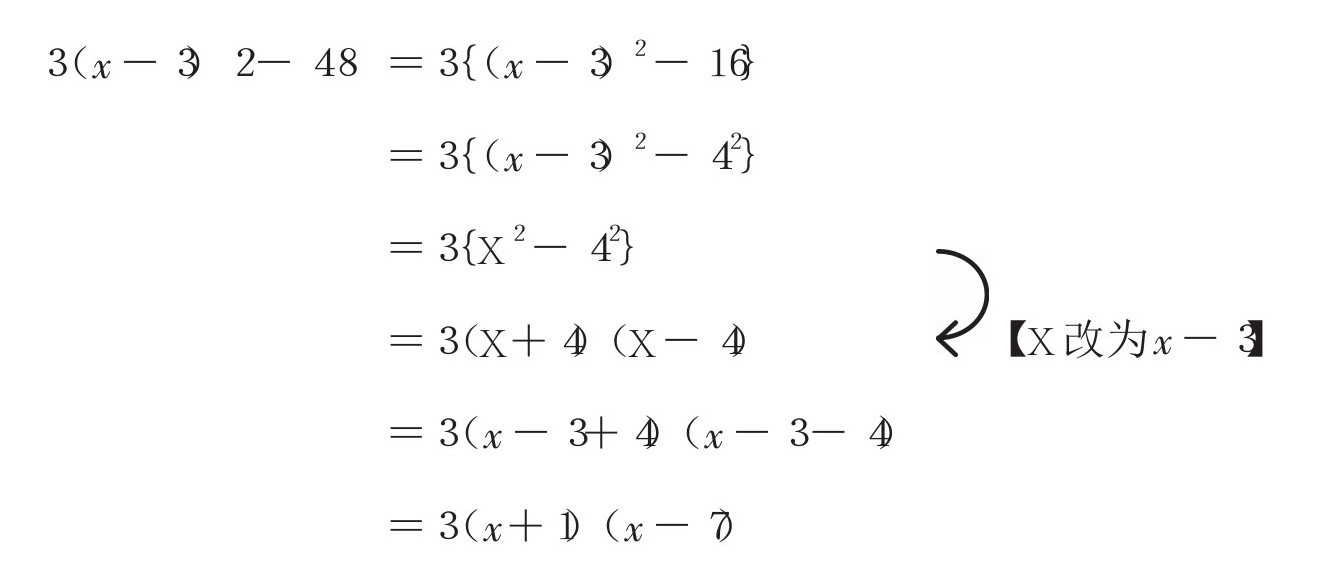
式子③有些复杂,而且其中没有共有的因数,这时就需要参考因式分解的基本要求“对最低次的文字进行整理”。我们通过式子可以得知,a是2次、b是3次、c是1次。c为最低次,所以我们就要对c进行整理。
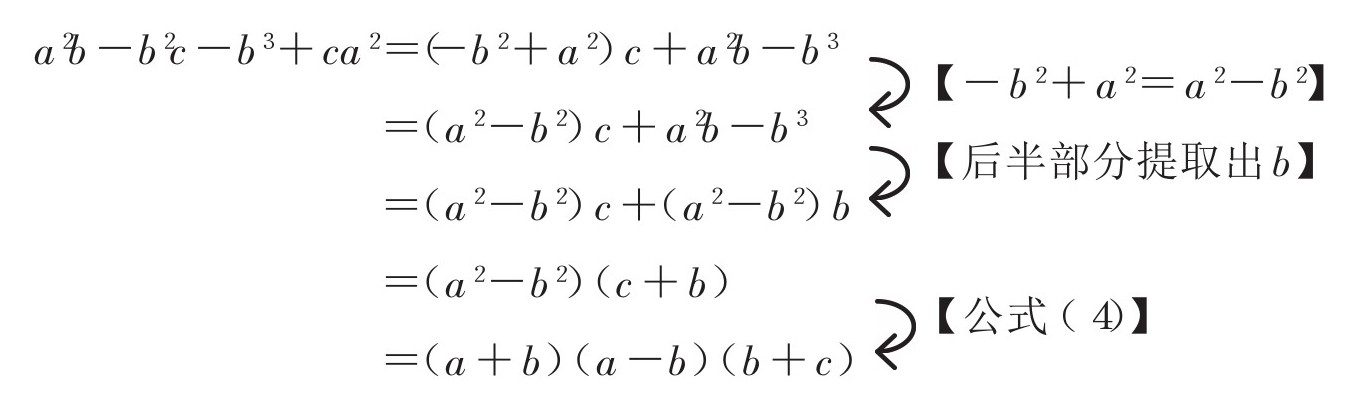
对二次方程进行因式分解,我们会切实感受到式子释放的信息量变多了。在下一章,我将对一次方程、二次方程的解题方法进行详细介绍。