




数学与算数最大的差别在于,解答数学问题会使用负数和字母。我们已经在上一章学过负数。那么,为什么数学会使用字母呢?简而言之,是为了抓住事物本质。例如,
-1、0、3、8、15、24、35、48、63、80、99……
大家知道这些数字之间有什么联系吗?如果你发现了其中的奥秘,说明你的洞察力相当敏锐(其实是有些难度的)。在描述这些数字之间的关系时,我们就需要代入一个字母。
n 2 -1(n为正数)
如此一来你就明白了吧——上面的数是平方数(某个数平方后得到的数)减去1之后得到的数字。其实字母不具备具体属性,无法明确表达意义,却能帮助你发现本质,你可以用一个列式表示所有拥有同一性质的数。
比如,如果你想列举所有的偶数,用数字的话,根本不可能完成。
0、2、4、6、8、10、12、14、16、18、20、22、24、26……
写到最后,你只能用“……”表示省略。但是,使用字母后,你只要写成:
2n(n为整数)
这个简单的数字字母组合就能代表所有的偶数,这就是所谓的“一般化”。
本质指的就是概念。我们在前一章提到过负数和无理数,这两种数都需要借助概念才能理解,可以说,理解“概念”是学习数学的一大目标。
一旦使用字母代替数字,我们便走进了代数(algebra)的世界。
代数,是9世纪的波斯数学家阿尔·花剌子模的著作——IIm al-jabr wal-muqubalah中“al-jabr”的词源,原本是“移项”的意思。阿尔·花剌子模又被称为“代数之父”。
“某个数的5倍减去3等于7。这个数是多少?”代数起源于3世纪,这种语言描述形式的文辞代数(rhetorical algebra)是代数发展的第一阶段。你也许会觉得这样的描述很啰嗦,如果使用字母和符号,这个问题就可以用下面的式子表示。
5x-3=7
这种算式(代数式)最早出现于17世纪。完善这种符号代数(symbolic algebra)的正是那位因“我思故我在(《方法论》)”而闻名天下的笛卡尔。
在式子中使用字母时,必须遵守几个规则,下面我们就来整理一下。
代数式的规则
规则1:省略乘法运算的符号(×)。
a×b=ab
规则2:数字与字母相乘,数字要写在前面。
a×3=3a
规则3:相同字母之积写成乘方。
a×a=a 2
规则4:不使用除法运算符号(÷),除法用分数表示。
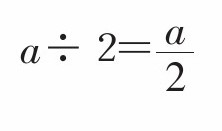
与“1”或“-1”相乘时,1要省略,这点需要特别注意。
1×a=a
(-1)×a=-a
另外,看到代数式时,一定要时刻想着“1”可能被省略了。在式子变形时,这一点非常重要。
【例】

我们一开始就说过,在算式中使用字母,可以帮你抓住算式的本质。假设你不知道三角形的面积公式,有人给你看了下面这张图,
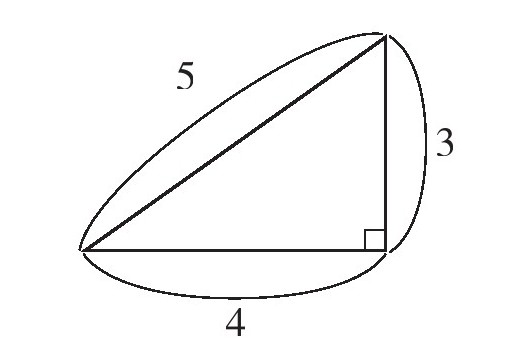
然后告诉你“这个三角形的面积是6”,不知你能否发现“6”是这样计算出来的:
4×3÷2=6
或许,你会误以为“6”是这样算出来的:
5+4-3=6
如果别人给你的图是这样的,并告诉你“这个三角形的面积是1/2ab”,你就能立刻发现它的本质:
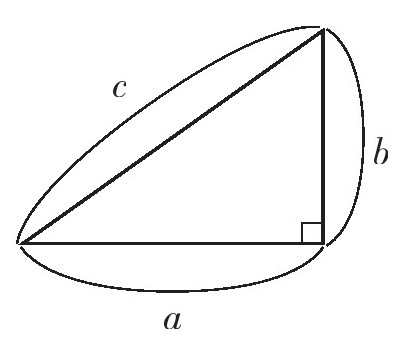
三角形的面积=
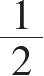 底边长×高(=底×高÷2)。
底边长×高(=底×高÷2)。
如果再遇到下面的三角形,你就能准确地求出它的面积。
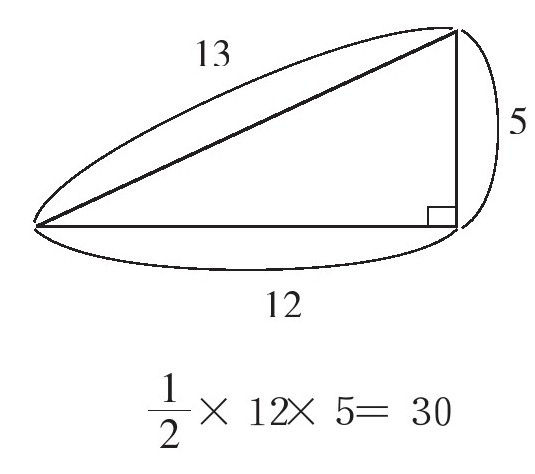
这就是字母的作用,认识到这一点非常重要!学会代数式的表达,并熟练将其应用于具体事例,你会发现很多复杂的东西都能变得很简单。
抓住事物的本质,总结出共同的概念,这就是所谓的一般化。数学的基本精神,就是从多个具体事例中找出潜藏的本质。因此,在学习数学过程中,我们应该随时想到用字母来表示对象。
以三角数为例。将物品以三角形式排列,我们会得到一串数字:1、3、6、10……我们将这些数字称为三角数。
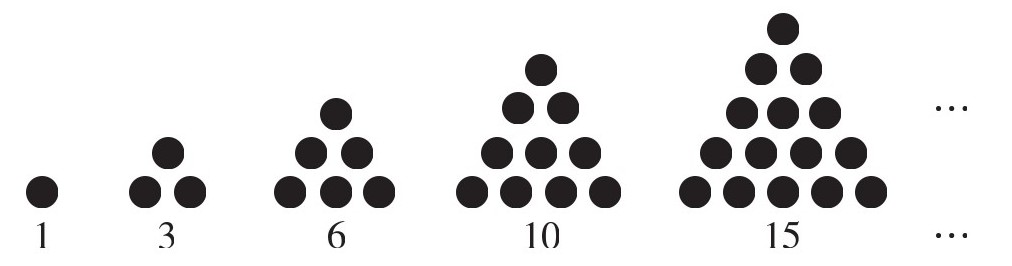
这里列举了5个数,那么,第10个数是多少呢?
“等一下,我画图看看……”
如果你肯这么费心地解答我提出的问题,那我不得不说,你真是个有耐性的人啊。但是,如果我问你第100个三角数是多少呢?我想,即便你再有耐性也不想画,一定会说:“我怎么知道。”
但是,如果你知道三角数可以用下列代数式表示,
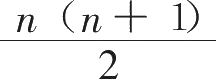 (n为自然数)就能轻松计算出第10个数:
(n为自然数)就能轻松计算出第10个数:
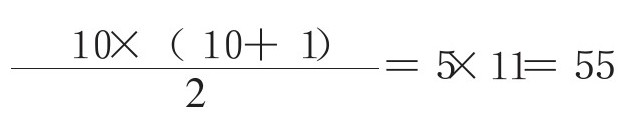
即便是计算第100个三角数,也不在话下。
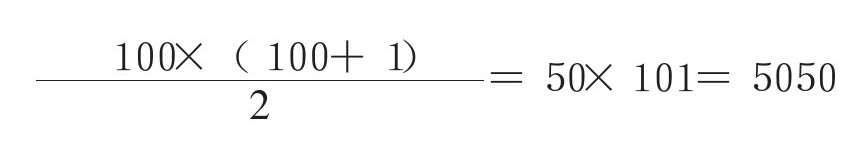
用字母表示对象,实现一般化,就能轻松解决麻烦的问题,是不是很神奇?
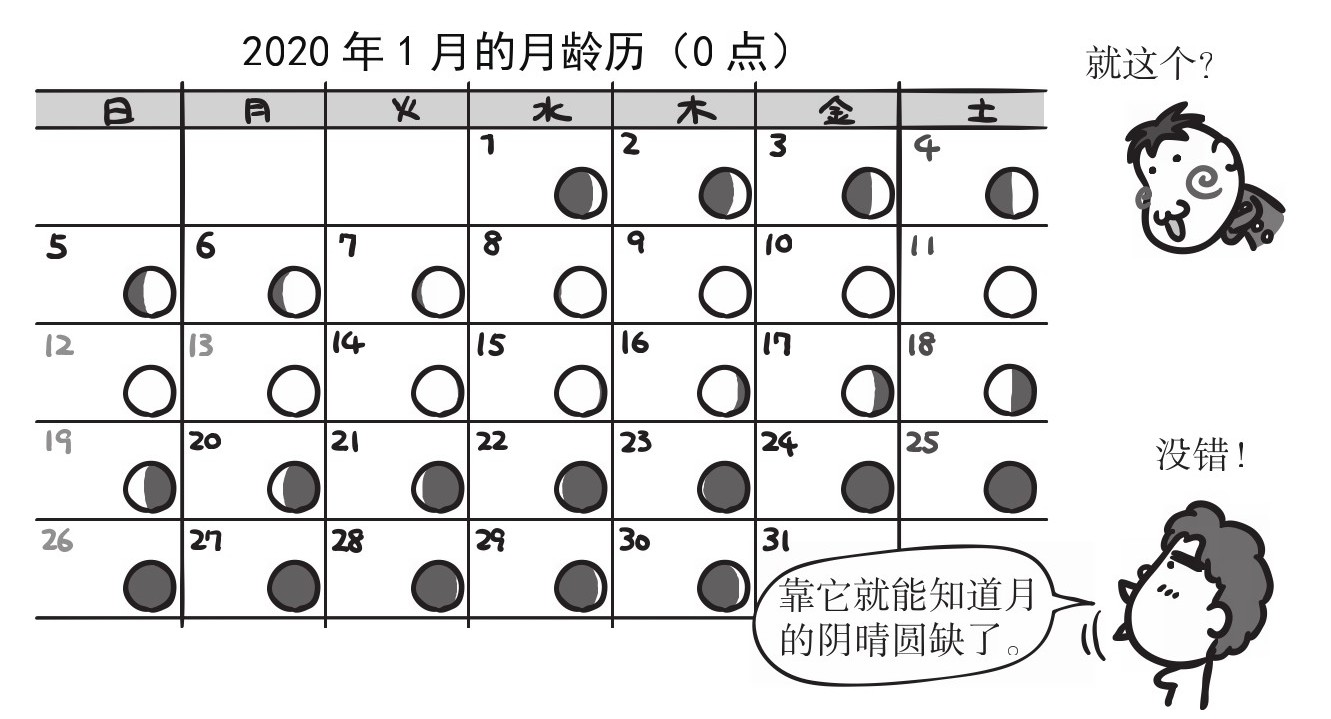
我再举个例子。大家听说过“月龄历”吗?
月龄历上记下了月亮一整年的圆缺情况,市面上有许多种类。另外,在某些网站也能查到指定日期的月龄,不论是多少年以前的,都能查到,你知道这是为什么吗?顺便说一句,这世上可不存在“天气日历”哦。
y年m月d日的月龄a可以用以下公式求出。

p(m)是每月都会变化的补充项,所以应根据所求月份,代入下列表格中的值。

例如,我们要求出2020年1月1日的月龄。
将y=2020、p(m)=0(根据上表)、d=1代入上面的公式。

因此,月龄为5日。
该公式是简略版的,所以最多会出现2天的误差。在一些能进行详细计算的网站上查询,2020年元旦的月龄是5.4日,所以差不了多少。
月龄可用代数式表示,因此我们能轻松地算出指定日期的月龄。但是,目前我们完全不能通过将日期代入某算式,得知该日期的天气状况。也就是说,月龄被一般化了,但天气并未一般化,即便是天气预报,也经常报不准。
我们来做几个练习,试着借助一般化的概念,解决一些简单的问题吧。题目的内容冗长,我们的目标是用代数式来表示它!
问题
已知某个自然数能被9整除,同时各位数字之和也能被9整除。假设该自然数是个3位数,证明上述假设成立。
[涉谷教育学院幕张高中]
【答案】
问题中出现的是“3位数的自然数”,首先,我们要考虑用字母来表示。这是十进制的计算题,在序章中,我们已经了解了部分和十进制相关的知识,比如,当我们看到789这个数时,会根据所学知识认为,789是由7个100、8个10、9个1组成。也就是说,我们会下意识地认为789是这么构成的:
789=100×7+10×8+1×9
假设百位数为a、十位数为b、个位数为c的数,我们可以用以下代数式表示一个3位数。
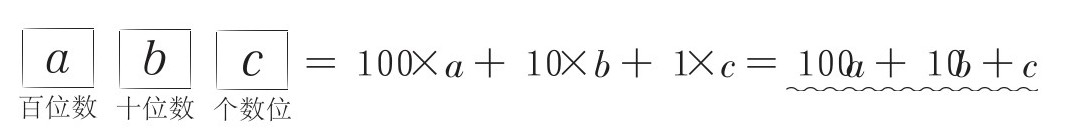
接下来用字母表示“能被9整除”的数也就简单了。能被9整除,就相当于是9的倍数。9的倍数是“9×整数”,所以设m为整数,那么能被9整除的数,就能用9m表示了。综上所述,“某个3位数的自然数能被9整除”这句话,可以“翻译”成下列算式。
100a+10b+c=9m(m为整数)……①
将文字应用题改成算式(先随便取个名字,就叫“数译”吧)的方法,第3章中会详细解说。
“各位数字之和也能被9整除”,这句话可以转换成下面的代数式。
a+b+c=9×整数……②
现在我们要对①式进行变形,去掉c。
消去c的原因,将在下一章讲述。
根据①得出,
100a+10b+c=9m
⇔c=9m-100a-10b ……③
将③代入②。
a+b+c=a+b+9m-100a-10b
=(1-100)a+(1-10)b+9m
=-99a-9b+9m
=9×(-11a-b+m)
因为a、b、m为整数,所以“-11a-b+m”也是整数。
没错,上面的式子已经变形成下面的等式(②的形式)了。
a+b+c=9×整数
也就是说,我们已经得出了a+b+c(各位数的和)是9的倍数(能被9整除数),这个结论。
上述内容证明了“3位数的自然数能被9整除的同时,各位数的和也能被9整除”。
不熟悉式子变形的人,请认真阅读接下来的“式子的计算(初中2年级)”。这里最重要的不是式子变形,而是用字母表示“3位数的自然数”或“能被9整除的数”,这就是一般化的过程。3位数的自然数是100~999,一共有900个,能被9整除的数不计其数,但只要用1个式子来表示,就能完全列举。
使用字母实现一般化,会将具体的描述转化成抽象的代号。但是,使用字母能表示无穷尽的数,还能抓住事物的本质,你难道不觉得很神奇吗?毫不夸张地说,通过符号代数,数学实现了向抽象世界的飞跃!