




生活在公元前5世纪的古希腊人,坚信所有的数都可以用整数的比(分数)来表示。特别是以哲学家毕达哥拉斯为首的毕达哥拉斯学派,认为“数是万物之源”,他们就像信仰神明一样,忠实地坚信整数和整数的比,甚至给数字1~10下了如下“定义”,也就是所谓的“毕达哥拉斯数秘术”。
毕达哥拉斯数秘术
1:理性2:女性3:男性4:正义●真理
5:结婚6:恋爱与灵魂7:幸福8:本质与爱
9:理想与野心10:神圣的数
毕达哥拉斯数秘术也可用于计算,例如,
2+3=5是“女性+男性=结婚”
2×3=6是“女性×男性=恋爱”
2+5=7是“女性+结婚=幸福”
3×3=9是“男性×男性=野心”
是不是觉得很容易?当然,万事不能一概而论。与一般人相比,数学家更能感受到每一个数字的“个性”,因此,他们这样定义数字也是可以理解的。顺便说一句,占星术和塔罗牌占卜术都源于毕达哥拉斯数秘术。
虽然当时的古希腊人认为,整数和整数的比能描述一切数的概念,但是在已被神化的毕达哥拉斯学派中,已经有人察觉到,其实世上存在无法用整数的比来表示的数。最讽刺的是,那个数的存在,还是通过毕达哥拉斯定理(也称勾股定理)证明出来的。
勾股定理(毕达哥拉斯定理)
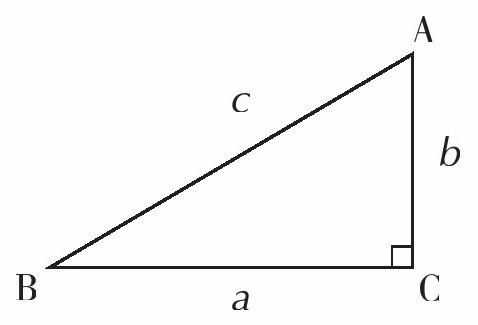
两条直角边的平方之和等于斜边的平方。
在左侧的直角三角形ABC中,
a 2 +b 2 =c 2 是成立的。即,
详细内容参见第6章“令人信服”。
毕达哥拉斯学派的希帕索斯发现,下面这种直角三角形的斜边长度c无法用分数表示。
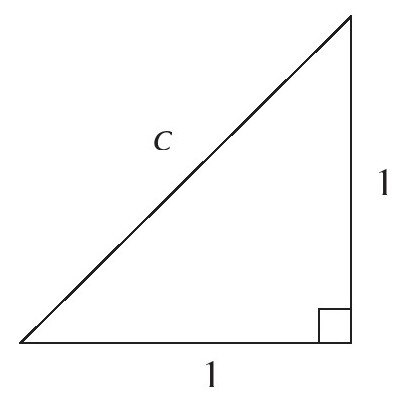
据说,当时听到这一说法的毕达哥拉斯非常震惊,要求所有弟子不得向外界泄露这个数的存在,甚至为了维护自己的权威而杀害了希帕索斯。希帕索斯发现的这个无法用整数的比(分数)来表示的数,就是无理数(irrational number)。
irrational number是指无法用比(ratio)来表示的数,所以有些人认为不应该将其翻译成“无理数”,翻译成“无比数”更贴切。
在讲解无理数之前,我先来复习一下平方根。首先从定义开始:“平方”是指自乘,“根”是指自乘的数。
平方根的定义
一个数平方后等于a,这个数则被称为a的平方根。
换言之,a的平方根是指下面这个等式的解,即x。
x 2 =a
例如a=4,
x 2 =4
则,
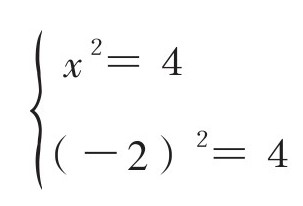
所以,
x=2或x=-2(x=±2)
因此,4的平方根就是2或-2(有2个!)。
一般来说,a为正数时,a的平方根有正负2个,可写成“±x”。“±”读作“正负”。
那么,7的平方根是什么呢?哪个数字自乘后等于7呢?想必没人能说的出来吧。因此为了描述这种数字,我们要引入一个新的符号,那就是√(根号)。
√(根)根号的定义
在a的2个平方根中,正数根用√a表示,读作“根号a”。
之所以特别强调“正数”,是因为正负的概念在之后(高中数学)的学习中非常重要,一定要特别注意。
使用√后,平方根便可以这样表示。
a的平方根是√a和-√a(±√a)
a的平方根是“x 2 =a”的解,因此,
x 2 =a,
x=±√a
所以说,7的平方根就是±√7。
我们已经知道,4的平方根是±2。使用根号后,4的平方根就变成了±√4。难道4的平方根有2种表示?完全正确。
±√4=±2
一般来讲,如果里面的数字是平方数(某个数自乘后得到的数),就可以像下面这样去掉根号。
去掉√的方法
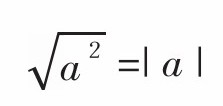
请注意,等号右边是绝对值。
我之前强调过,在a的平方根中,正数的平方根用√a表示。即,
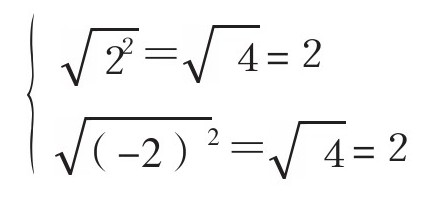
所以,
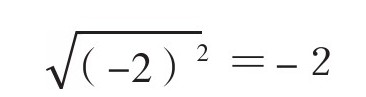
这个结果是错误的,应该是,
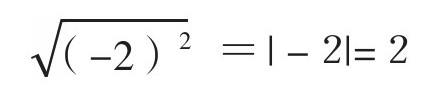
接下来我要介绍的是数的种类。
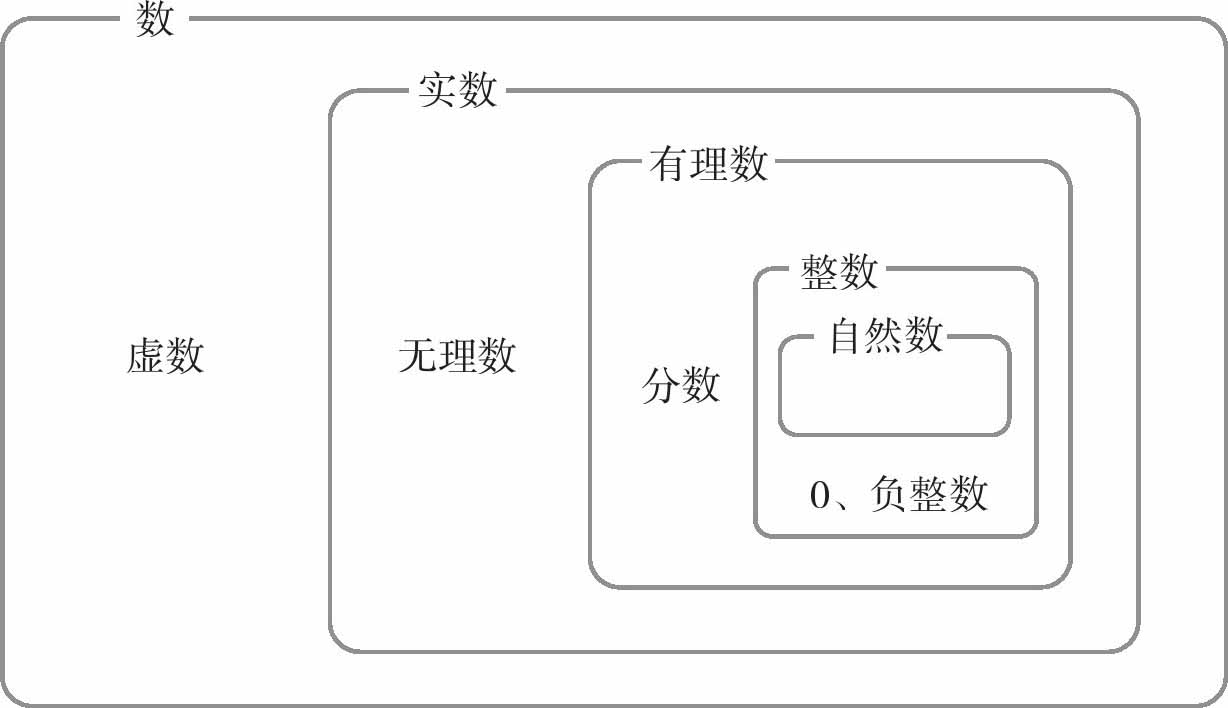
虚数(imaginary number)是指平方后得到负数的数,而这已经超出了初中数学的范围,到了高中才会学到。
有理数(rational number)是指可以用分数,也就是比(ratio)来表示的数。整数可以用分数表示,所以属于有理数。
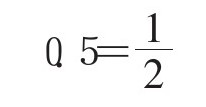
另外,像下面这种,
0.33333333…
0.18181818…
小数点后面重复出现相同数字的小数(又叫作循环小数),也可以用分数表示,所以也属于有理数。

我们之前提到过,无法用分数表示的数被称为无理数,如√2、-√5、3√7、π(圆周率)等,都是无理数。
利用英文简单记忆圆周率
用单词替换数字:
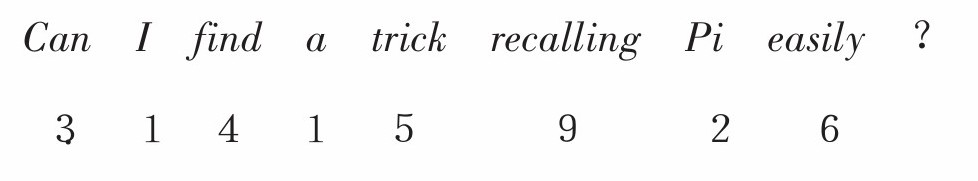
学习数学虽然无需背诵公式和解题方法,但是还是要知道一些数字的概念。无理数的概念对概算有很大的帮助,所以最好记住。
在这一节的开头我曾经提到过,发现无理数的希帕索斯被毕达哥拉斯和本学派的弟子们杀害,那么,为什么毕达哥拉斯宁可杀人也不肯承认无理数的存在呢?是因为不想让别人知道自己的理论是错误的吗?
我认为除此之外还有别的原因。以下纯属我的个人推测:可能毕达哥拉斯等人一直坚信,世间万物都可以用数字表示,而无法用分数表示的无理数,是只有“大概值”的数。比如,我想知道(估算)√5到底等于几。
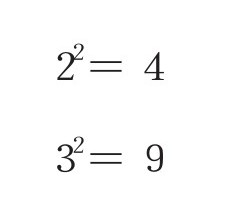
因为,
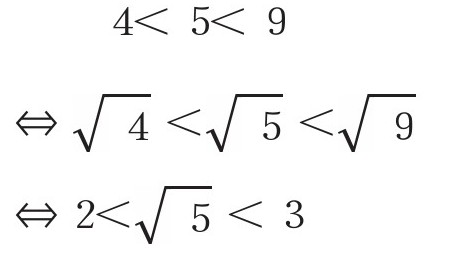
所以我们能得知,√5是介于2和3之间的数。接着再进一步计算,因为,
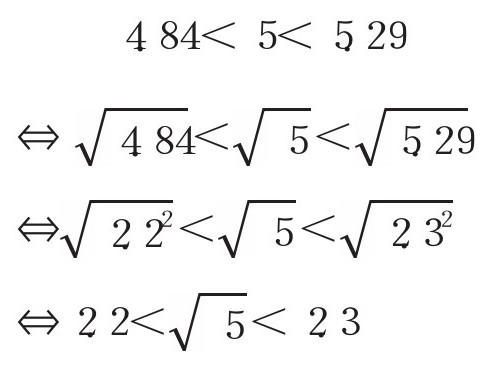
通过推算,我们得出了上述结果,可无论怎么算,我们也无法准确地算出√5的值。
在数轴上,只能知道√5的大概位置。
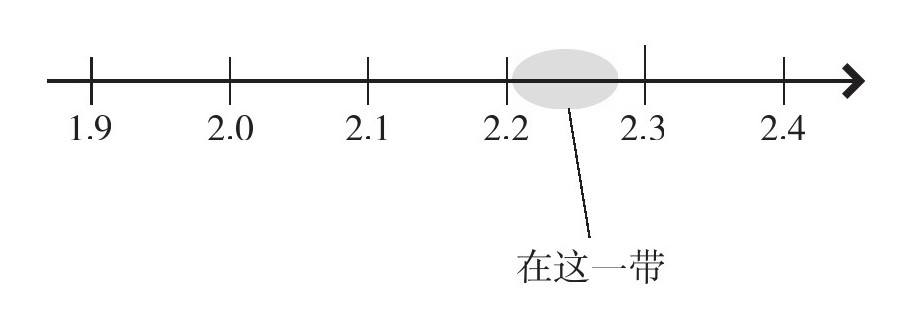
我想,这才是毕达哥拉斯最无法接受无理数的原因。
其实,爱因斯坦也曾遇到过类似的情况。20世纪20年代,有科学家发现,实物粒子也具有波动性,波长可以预测,物质波理论的提出开创了现代量子力学的时代(看不懂也没关系,可直接跳过)。换句话说,在微观世界里,一个粒子会出现在地点A还是地点B是不可以预测的。而对此,爱因斯坦强烈批评道:“神是不会掷骰子的。”他认为,在之前的物理学概念中,自然现象的未来遵循自然的法则,未来只有一种,但是,如今几乎没有一个科学家会怀疑量子力学。
毕达哥拉斯和爱因斯坦都想通过数学诠释自然现象,也许正是这种强烈的意念,导致毕达哥拉斯做出了过激的行为。
言归正传,“无理数”是我们最初遇到的“无法确定的数”。为了计算,自然数诞生了;为了分配、求算比例,分数诞生了;为了表示“无”的状态,0诞生了;为了在同一概念中掌握相反的概念,负数诞生了……这些数都有具体的数值,但无理数的值却难以确定。无理数只是个有大概值的数,但我们可以知道无理数自乘后的结果,这是不是很神奇呢?
我希望大家能通过认识“无理数”,学会从不同的角度理解事物的概念,只要有了这种认知意识,就能理解本不存在的虚数(平方后等于负数的数)。也许随着研究继续深入,我们会发现这个世界不是三维的,可能是“九维”乃至是“十维”的,而到那个时候,我们就不会觉得这种“超弦(玄)理论”不切实际了。
每个人都会对不了解的事物感到不安。如果能抛开事物的本体,在概念的层面思考问题,我们的思维就能在宇宙的尽头穿梭,认识基本粒子的世界。认识“无理数”,正是我们踏上自由之旅的第一步。
无理数平方根是难以确定的数,所以在加法和乘法的计算中,我们不能将其设为未知数(代数)。下面,我们要详细讲解代数式的计算。
【加法】
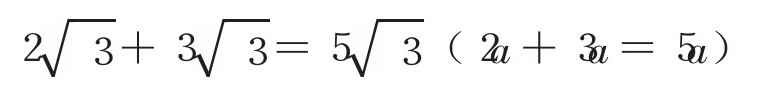
【减法】
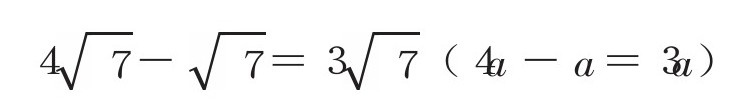
乘法和除法的计算过程更简单。
【乘法】
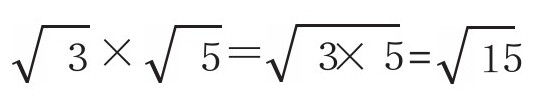
【除法】
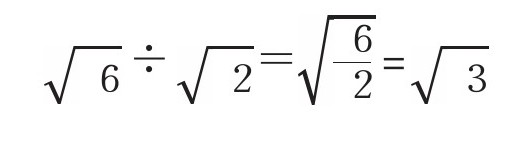
有些人可能会对无理数乘除法运算法则有疑问,我在此给大家分析一下。
现在,我们假设x是a的正平方根,y是b的正平方根。即,
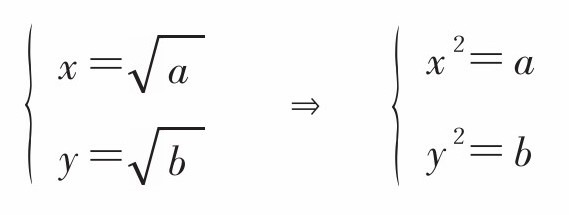
代入算式后,得出,
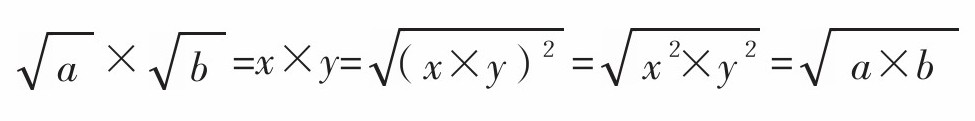
因此,
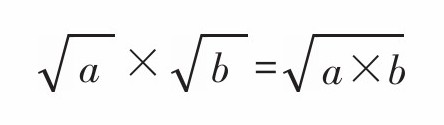
同上,除法只需将除法改成倒数的乘法计算即可。
包含2个以上的平方根的加减法,需要特别注意。
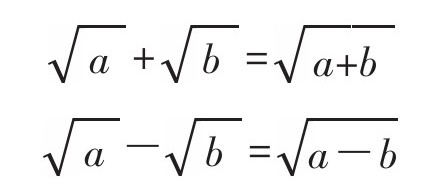
上面的算式是不成立的,你仔细一想,就会发现这样的计算是错误的。
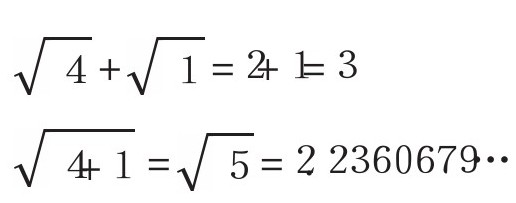
所以,
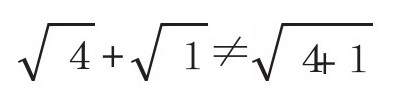
减法也一样,
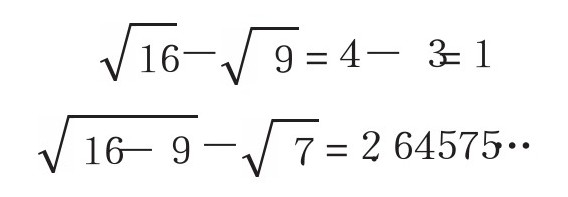
结果很明显:
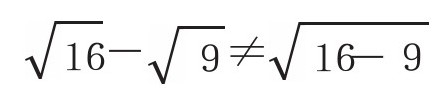
接下来我要介绍简单的平方根计算方法。
简单的平方根计算
a>0,b>0时,
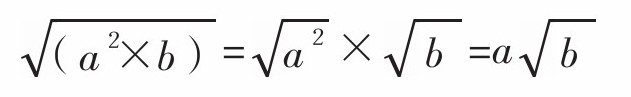
我们在前面已经学过,
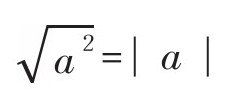
由于a>0,所以,
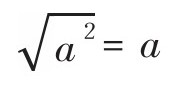
接下来,就让我们就具体应用一下吧。
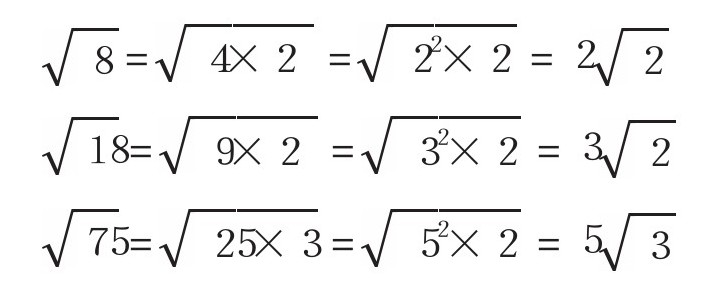
要想快速得出结果,就必须记住平方数(某个数平方后得到的数)。如果你能将1到15的平方数牢记在心,用起来会非常方便。
平方数
1,4,9,16,25,36,49,64,81,100,
121(=11 2 ),144(=12 2 ),169(=13 2 ),196(=14 2 ),225(=15 2 )