




2012年7月,“发现疑似希格斯玻色子的粒子”的新闻一经发布,马上成为当时最热门的话题。希格斯玻色子?一般人恐怕连听都没听说过,为什么这一发现能轰动全世界呢?
那是因为在20世纪60年代,有科学家提出物质世界中存在17个基本粒子,而希格斯玻色子是一直未被发现的基本粒子。如果希格斯玻色子不存在,就表示得到广泛认可的“标准模型”构想是错误的,由此也会引发一系列的严重问题。也就是说,希格斯玻色子的发现如果得到证实,就是一个“跨世纪的大发现”,可以补全历经50年发展至今的基本粒子物理学中缺失的一环。
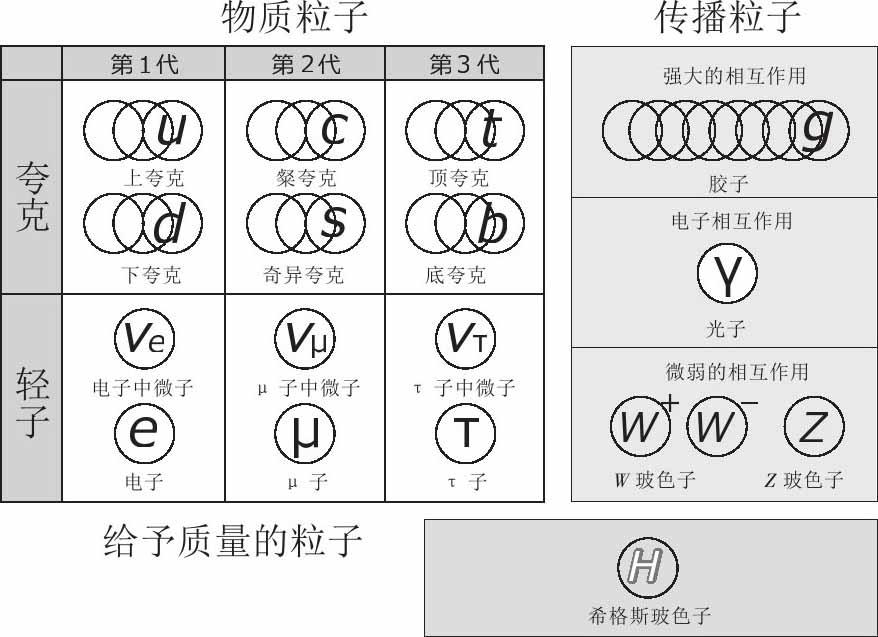
基本粒子构成的物质世界的“标准模型”
出处:作者参考高能加速器研究机构的研究结果,自行绘制
简而言之,基本粒子(elementary particle)是指不可分割的粒子,世界上的所有物质都由这17种基本粒子组成,他们是万物的基础。因此,这样的新闻不仅引起了科学家的广泛注意,也激起了许多人的求知欲(也许吧)。
从古至今,人类一直在追求万物的根源。比如,日本人认为万物的根源是“五元”,即风、火、土、金、水;而中国则借助“五行”的概念——金、木、水、火、土来解释森罗万象;同时,印度人认为风、火、地、水、空这五大元素是物质的“基础”;古希腊人则认为风、火、土、水这四大元素才是物质的“基础”。
人类追求万物根源的执着精神,与原子和分子的发现密切相关,正是这种精神引领着科学家们展开了对基本粒子的深入研究。
那么,在数的概念中,有像基本粒子这种“不可分割的‘基础元素’”吗?当然有!那就是“质数”。也就是说,质数就是数的基础。
质数的定义如下。
质数的定义
一个大于1的自然数,除了1和它本身外,不能被其他自然数整除。
具体是指以下的数字:
2、3、5、7、11、13、17、19、
23、29、31、37、41、43、47…
在此我们要特别注意,“1”不是质数。为什么呢?如果说定义就是这么规定的,那我们就没必要继续讨论了,其实如此定义也是有原因的。首先,我们要清楚“任何数被分解质因数后,只有一种表示形式”。如果质数中包括1,那么某个数被分解质因数时,就会出现以下这种情况:
6=1×2×3
6=1×1×2×3
6=1×1×1×2×3
如此一来,将一个自然数分解质因数,就会出现无数种答案。为了避免这种情况发生,我们才把“一”剔除在质数之外。说到这里,可能有人会问:为什么分解质因数非要拘泥于“一种表示形式”呢?分解质因数的方法只有一种,意味着某个数字与其分解为质数的方法之间成立“单射”关系。质数中不包含1,因此将6分解质因数后只能得到“2×3”这一个结果,而质因数分解为“2×3”的数也只有6。这种对应关系就是我们要强调的重点。
“单射”概念或许会让你觉得有些晦涩难懂,其实这就如同学校的鞋柜与鞋子、棒球队球衣与选手之间一对一的关系,如果能这样理解的话就一点儿都不难了。
如果“单射”关系成立,那么这个概念就能用其它表达方式进行阐述,你可以从另一个角度加以理解。
比如,

在上述推断中,田中的鞋柜和田中的室内鞋是一一对应的(译者注:为了维护学校的清洁,日本有进学校换室内鞋的传统),且田中的室内鞋和田中自己也是一一对应的,因此我们能根据田中的鞋柜没有室内鞋,从而得出田中还在学校里的结论(当然,如果田中已经回家,但是有人恶作剧拿走了他的鞋子,那就另当别论了)。综上所述,在逻辑推理中,单射关系是非常重要的。
详见第4章的“抓住因果关系”。
如前面所说,把一个自然数分解成若干个质因数的乘积的形式,即求质因数的过程叫作分解质因数。在这里,我大致介绍一下这个概念的定义。
因数:整数相乘,整数就是积的因数
质因数:顾名思义,既是质数又是因数
分解质因数的顺序
1)依此除以能整除的质数
2)把用于分解的质数和最后剩下的质数写成乘积形式
分解质因数时使用的短除号就是倒过来的除号,我们一起练习一下吧。
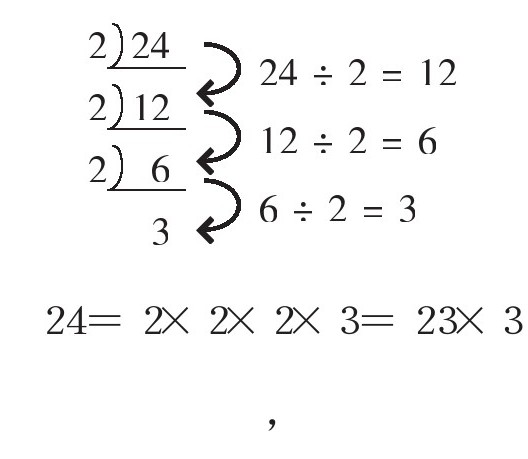
如此一来,我们就完成了24的分解质因数过程。也就是说,24可分解为3个“2”和1个“3”。
学会分解质因数后,我们就能清楚地知道指定的数是由什么“零件”(因数)组成。不仅如此,只要搞清楚数的“零件”,就能弄明白不同数之间拥有哪些相同的性质,从而展开各种推算。让我们通过接下来要学的公因数和公倍数,来加深对分解质因数概念的印象吧。
公约数的定义
两个或两个以上的整数,如果有一个整数是它们共同的因数,那么这个数就叫作它们的公约数,也称公因数。
【例】12和40
12的约数:1、2、3、4、6、12
40的约数:1、2、4、5、8、10、20、40
因此,12和40的公约数是有3个:1、2、4。公约数中最大的数被称为最大公约数,同时,各个公约数都是最大公约数的约数。到此为止,我们都可以通过计算的方式来理解。
我们也可以借助分解质因数的概念,去理解公约数。
首先我们要注意的是,某个数经分解质因数后,得到的因数(零件)一定是那个数的约数。
对12进行分解质因数:
12=2×2×3
其中,1个“2”和1个“3”相乘得出的“6”,就是12的约数。
先把数字12分解成“零件”,再将它的约数进行归纳,可得到如下表格。
【12(=2×2×3)的约数】
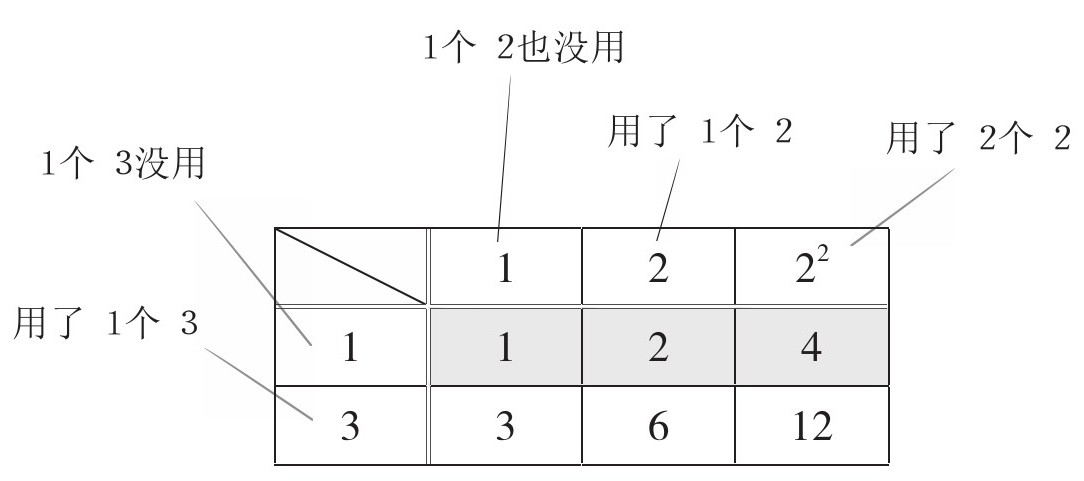
同样的道理,
40=2×2×2×5
40的约数可以通过如下表格进行归纳。
【40(=2×2×2×5)的约数】
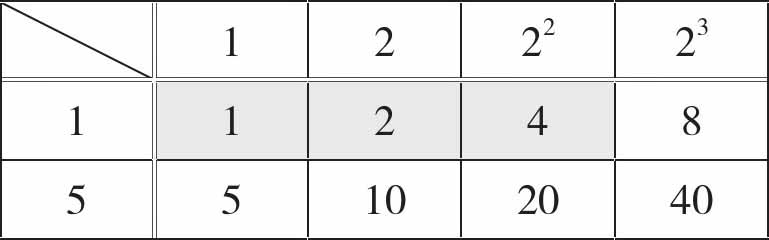
表格中灰色格子中的数,是12和40共有的“零件”,即公约数。只要经过分解质因数,数字共有的“零件”就能一目了然。
公倍数的定义
在两个或两个以上的自然数中,如果它们有相同的倍数,这些倍数就是它们的公倍数。
【例】4和6
4的倍数:4、8、12、16、24、28、32、36、40、44、48…
6的倍数:6、12、18、24、30、36、42、48、54…
因此,4和6的公倍数是12、24、36、48……公倍数中最小的数,被称为最小公倍数,而所有的公倍数都是最小公倍数的倍数。以上内容也都属于计算范畴。
让我们继续借助分解质因数来理解公倍数吧。
4和6分别进行分解质因数,
4=2×2
6=2×3
由此可见,双方共有的质因数(2),乘以其余的质因数(2和3),得出的结果(2×2×3)就是最小公倍数。
通过分解质因数来思考4和6的倍数,可用表格进行归纳,我们会发现“2×2×3”及其倍数是共有的。
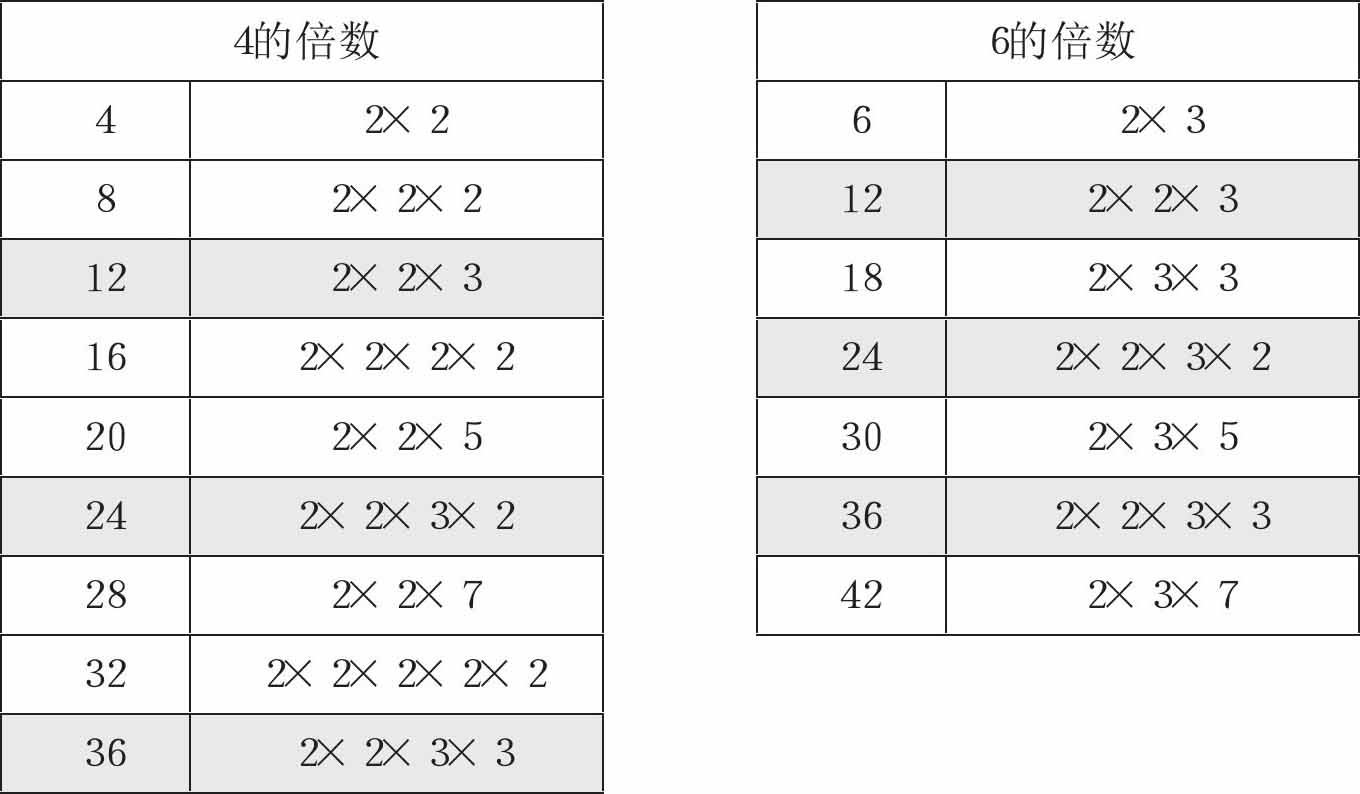
最小公倍数是统合(相乘)各自共有的零件(因数)与非共有的零件(因数)之后,得出的数。因此,几个数共有的零件越多,公倍数就越小。比如,4和6的最小公倍数是12,但4和9由于没有共同的因数(如下),
4=2×2
9=3×3
所以,它们的最小公倍数比12要大(如下)。
2×2×3×3=36
当两种想法并存时,共通的部分越多,越容易进行统合,但通常得到的结果只是已经存在的部分;当双方共通的部分较少时,虽然统合起来更加困难,但往往能合力取得更大的成果。
所谓的“革命”,通常是由非常规的思维引发的。原本完全没有关联的东西,经过组合从而诞生出新的东西,这种情况并不少见。一桥大学技术革新研究中心的教授米仓诚一郎先生曾经说过:“技术革新指的就是重组。”米仓先生举了几个例子,例如“化妆品与男性(男性化妆品)”“录音机与耳机(随身听)”“夜晚与商场(唐吉诃德)”(译者注:唐吉诃德是日本一家24小时不打烊的折扣百货店)等等。将那些没有关联的东西进行组合,就可能创造出令人震惊的巨大成果(价值),这与通过分解质因数得出公倍数的原理是相通的。
在某电视节目中,曾有人对某个人企业的总经理提出质疑,问为什么公司不采取合议制,而是由社长独裁专断。他当时的回答非常有趣:“最大公约数太小。”确实,不同要素之间的差异性越大,集合得到的“最大公约数”越小,小到最后可能只剩下“1”。公司要开会做一个决定,如果采取合议制,反而很难做出能带来最大利益的决断,这个观点我也认可。
团队在执行某个项目时,各干各的是最危险的,因为最终的项目成果,很可能变成各个成员之间的“最大公约数”,小之又小。
为了让项目创造巨大的收益,除了全员共有的“最大公约数”,充分发挥每个人的作用才是关键。
分解质因数告诉我们,将每个东西分解为“不可再分的质数”,无论是解决“公因数”还是“公倍数”的问题,都是最有效的方法。当然,发现事物的“质”绝非易事,但只要我们追根溯源,就能发现事物的本质,所以我希望大家在思考问题的时候不要半途而废,要有追根究底的精神。
千万不要小觑公约数、公倍数的概念。借助分解质因数的概念求出公约数和公倍数,能帮助我们发现不同事物的共同特点,还能对统合事物的难度和成果进行推测,是一项非常实用的技术。
让我们来挑战一下高中的入学考试题吧。要注意,最大公约数是共有的因数,而最小公倍数是共有的因数及其他因数之积。
问题
2个自然数的最大公约数为3、最小公倍数为210,它们的和为51。求这2个数分别是什么。
[青山学院高中部]
【答案】
假设2个数中较小的数为x,较大的数为y(x≤y)。
最大公约数为3,意味着x、y共有的因数(零件)只有3。即,
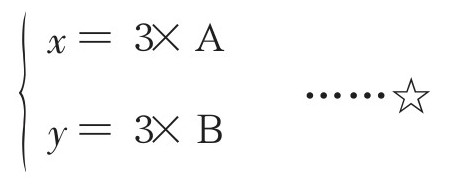
这里要注意的是,A和B没有共有的因数(二者皆为质数),由于x≤y,我们可得出A≤B(后面会用到)。
另外,2个数的最小公倍数为共有的因数3及其他因数(A和B)相乘之积。题干中提到2数的“最小公倍数为210”,
210=3×A×B
∴A×B=70
“∴”是表示“所以”的数学符号,下文中会经常出现。
为了分别求出A和B,我们先把70进行分解质因数(如下)。
70=2×5×7
因此,
A×B=2×5×7
由于A和B没有共有的因数,且A≤B,所以A和B可能为下列组合之一。

将这些可能代入☆号算式中,得出x与y的可能答案。

到这里,我们就要使用最后的条件啦——“和为51”。代入后……没错!
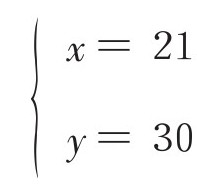
因此,这2个数为21和30。