古怪的数学题

解方程的时候，可能会碰到一些情况，让没有足够数学经验的人不知所措。下面，我们就来举几个这样的例子。

例1：有一个两位数，它十位数上的数字比个位上的数字小4。如果把十位和个位上的数字对调，新得到的两位数比原来的两位数多27。求这个两位数。

假设这个两位数十位上的数字是x，个位上的数字是y，根据题意可得到下面的方程组：

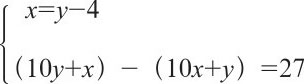
将第一个方程代入第二个方程，可得到下面的方程：

[10y+（y-4）]-[10（y-4）+y]=27

化简得到：36=27

也就是说，我们没有得出x和y的值，反而得到了一个矛盾的等式，这是怎么回事呢？

这说明，要求的两位数是不存在的，因为方程组中的两个方程是矛盾的。

化简第一个方程得到的是：y-x=4

化简第二个方程得到的是：y-x=3

上面两个方程的左边都是（y-x），但第一个方程的右边是4，而第二个方程的右边是3，显然这是矛盾的。

在求解下面的方程组时，也会遇到类似的问题：

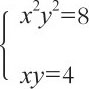
两个方程的两端分别相除，可得到下面的方程：

xy=2

第二个方程是xy=4，对比可得出这样一个结论：4=2，显然这是不可能的。所以，满足这个方程组的数也是不存在的。一般我们称这种情况为“不相容”方程组或“矛盾”方程组。

例2：把例1中的已知条件稍加改变，又会遇到另一种意外的情形。比如，已知这个两位数十位数上的数字比个位上的数字小3，而不是小4，其他条件不变，求这个两位数。

假设这个两位数十位上的数字为x，个位上的数字则为x+3，可得到类似例1中的方程：

[10（x+3）+x]-[10x+（x+3）]=27

通过计算，可得出：

27=27

显然，这个等式是恒等式，但我们并未计算出x的值。是不是不存在这样的两位数呢？

情况刚好相反，这个恒等式说明，无论x的值是多少，方程永远成立。事实上，也很容易验证这一点，题目中讲到的已知条件，对于任何一个十位上的数字比个位上的数字小3的两位数来说，都是成立的，比如：

41-14=27

52-25=27

63-36=27

74-47=27

85-58=27

96-69=27

例3：有一个3位数，满足以下条件：

（1）十位上的数字是7；

（2）百位上的数字比个位上的数字小4；

（3）如果把这个三位数颠倒过来写（即个位与百位上的数字互换），新得到的数比原来的3位数大396。求这个三位数。

假设这个3位数个位上的数字为x，则有：

100x+70+x-4-[100（x-4）+70+x]=396

化简上面的方程，得到：

396=396

通过例2的经验，我们知道这个结果表示：任意一个三位数，只要它百位上的数字比个位上的数字小4，不考虑十位上的数字，那么，如果把这个三位数颠倒过来写，得到的新数就会比原来的那个数大396。

上面讨论的这些问题都比较抽象，之所以列举这些例子，就是为了帮助读者养成一个习惯：遇到这样的问题，把方程列出来，剩下的就是求解方程的问题了。现在，我们已经有了这样的理论知识，接下来就能解决日常生活、体育或军事方面的问题了。 EJxFDOQAHMwp0g4gzXXOWyJt8R+gatyM/sLOxKhkPPCO1RgD+7ndPH5VrnQrNC9o