




【题目】一个割草组接到了一项任务,要把两块草地上的草割掉,其中大块草地的面积是小块草地面积的2倍。上午,割草组的所有人都在大块草地上割草;下午,他们对半分开,分别到两块草地上割草。到了晚上,大块草地上的草都割完了,小块草地上的草还剩下一小块,需要一个人花一天的时间才能割完。(图6)

图6
假设割草组所有的人割草速度都一样,请问,这个割草组共有多少人?
【解答】假设割草组的人数是x,此外还需要另一个辅助未知数,即每个人每天割草的面积数,可用y来表示。先用x和y表示出大块草地的面积。根据题意,在上午,x个人割草的面积是:
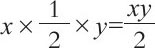
下午,只有一半的人割剩下的草,即只有x/2个人割草,这些人割的草地面积是:
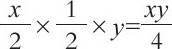
所以,大块草地的面积是:
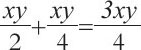
我们再来看如何用x和y来表示小块草地的面积。下午,x/2个人在这片草地上割了半天,那么,他们割的一共面积是:
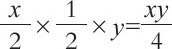
这时,还剩下一小片,其面积刚好是y,也就是一个人在一天的时间里割草的面积。所以,小块草地的面积是:
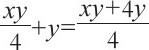
因为大块草地是小块草地面积的2倍,所以:
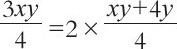
化简后,可得:
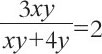
约掉方程左边的辅助未知数y,方程就变成了下面的形式:
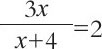
即:3x=2x+8
解得:x=8
也就是说,割草组一共有8个人。
在《趣味代数学》第一版出版后,我收到了A.B.齐格教授寄给我的一封信,他在信中谈到了这道题目,并认为这道题的意义在于,它不能算是一道代数题,而是一道简单的算术题,根本没必要用这种死板的公式来求解。
教授还说:“关于这道题的来龙去脉,其实是这样的。我的叔叔伊·拉耶夫斯基和列夫·托尔斯泰是很好的朋友,以前我的父亲和叔叔一起在莫斯科大学数学系学习。当时的数学系课程中,根本没有关于教学法的内容,所以学生们就要到对口的城市公民中学实习,跟那些有经验的中学老师一起探讨教学方法。在他们的同学中,有一位叫彼得罗夫的人,他是一个很有天赋和创造力的人,可惜他身患肺痨,英年早逝。彼得罗夫提出过这样的观点:课堂上教的算术不是教会学生学习,而是毁了学生,因为过于僵化的教学模式会束缚学生的思维,让他们只能用固定的方法解决固定的问题。为了证明自己的观点,他甚至想出了很多题目。这道割草的题目就是其中之一。这些灵活多变的题目难住了那些‘有经验的优秀的中学老师’。那些没有接受过刻板教学的学生,却很容易地解开了这些题目。对于那些有经验的优秀的老师来说,借助方程式或方程组,能够把这道题目解答出来,但是事实上只需要通过简单的算术计算,问题就解决了。”
接下来,我们就看看如何使用简单的算术方法解答这道题。
大块的草地需要全组的人割半天,再加上半组的人割半天,所以半组人在半天的时间里,共可以割这块草地的1/3。所以,小块草地剩下的那块就是1/2-1/3=1/6,而一个人一天刚好可以割完这部分。在一天中,全组人一共割草的面积是:6/6+1/3=8/6。所以,割草组的总人数就是8人。
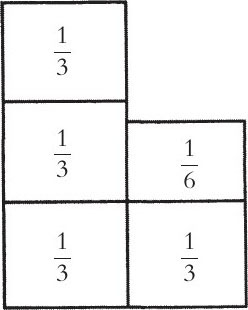
图7
托尔斯泰很喜欢这类有变化但又不是太难的问题。当他听到这个题目时,提出该题目还可以通过图形来求解,如图7所示。那是最简单的图,也很容易让人理解。
下面再来看几道题目,这些题目都能用巧妙的方法来求解。