
下载掌阅APP,畅读海量书库
立即打开




【题目】河的两岸长着两棵棕榈树,它们隔岸相对。其中一棵树高30肘尺(古代的长度单位,大概等于肘关节到手指尖的长度),另一棵树的高度是20肘尺,两树之间相距50肘尺。在两棵棕榈树的树梢上,分别落着一只鸟。忽然间,两棵树之间的河面上出现了一条鱼,两只鸟都看到了这条鱼,并同时朝着这条鱼飞过去,最后同时到达了目标,如图4所示。
试问,这条鱼距离30肘尺高的棕榈树的树根有多远?
图4
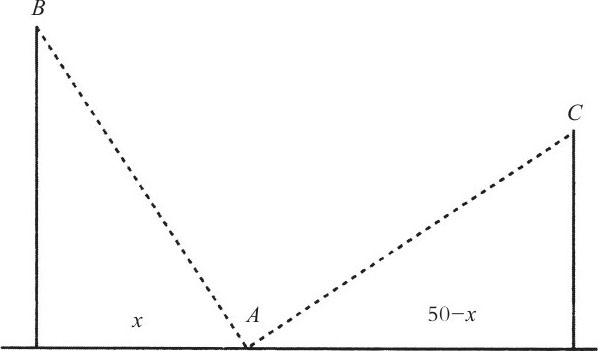
图5
【解答】如图5所示,根据勾股定理,可得出下列关系:
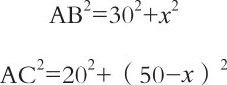
由于两只鸟飞到A处所用的时间相同,即可得到AB=AC(此处认为鸟的飞行速度无差别)。所以有:
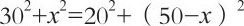
简化后,可得:
100x=2000
即x=20。
也就是说,这条鱼距离30肘尺高的棕榈树的树根有20肘尺。