我最喜欢的趣味代数书最新章节_洛维奇·别莱利曼著

共有多少种可能的国际象棋棋局

在本节中，我们粗略地计算一下，在国际象棋的棋盘上，共可能出现多少种不同的棋局。这里只是想让大家知道，这个数目究竟有多大，非常精确的计算没什么意义，所以我们只是估算。有本书叫作《游戏的数学和数学的游戏》，里面有这样一段文字：

由于白方的每个卒都能向前走1个格或2个格，共有8个卒，16种走法。2个马分别有2种走法，共有4种走法。所以，白方的第一步共有16+4=20种走法。同样，黑方的第一步也有20种走法。白、黑两方各走第一步之后，会出现20×20=400种不同的棋局。

走了第一步之后，后面的走法就更多了。比如，如果白子第一步走的是e2-e4，那么，第二步就有29种走法。再走第三步，可能走法还会更多。以王后为例，假设它本来在d5格中，且它所有的出路均为空格，那么它可能的走法就有27种。不过，为了计算更简单，我们不妨取它们的平均数：

在双方的前5步中，假设每步的走法都是20种，在以后的每一步中，假设每步的走法是30种。另外，假设双方在比赛中各走了40步。这样，我们就能计算出，在这盘比赛中，所有可能的棋局数目是：

（20×20） ⁵ ×（30×30） ³⁵

要求出上式的近似值，我们可以对上式进行一些变形：

上式中，用20 ¹⁰ 代替10 ³ ，是因为20 ¹⁰ ≈1000=10 ³ 。

对3 ⁷⁰ 可以进行下面的近似：

于是，有：

传说中，奖给象棋发明者的麦粒数是（2 ⁶⁴ -1），这个数大概是18×10 ¹⁸ ，象棋的棋局数比这个数大很多。假如地球上所有人每天24小时都在下棋，假设每走一步需要1秒钟，那么，想把这些棋局全部实现，大概需要10 ¹⁰⁰ 个世纪！

自动下棋机中隐藏的秘密

出现可以自动下棋的机器，你肯定觉得很神奇。棋子在棋盘上的不同组合有很多，甚至可以说是无限多个。倘若告诉你，历史上曾经出现过可以自动下棋的机器，你一定觉得不可思议：怎么可能制造出这样的机器呢？

事实上，这不过是人们的美好愿望罢了，并不是真的出现过自动下棋的机器。匈牙利有一个叫沃里弗兰克·冯·坎别林的机械师，因为发明了一种能够自动下棋的机器而声名远扬。据说，他曾经在皇宫里展示过这一机器，继而又在巴黎和伦敦进行过公开的展览，甚至连拿破仑都想跟这台机器较量，并坚信自己能够取胜。在19世纪，这台机器被带到了美国，不幸在费城的一次大火中被烧毁。

据说，当时还出现过一些其他的自动下棋机，只是不如上面介绍的那台那么有名。不过，人们并未因此灰心，而是一直致力于发明一种能够进行有效运算的机器。其实，那时候发明的这类机器，都无法真正实现自动运算。很多时候，在机器的内部藏着一位棋手，他不停地移动棋子。虽然这种机器看起来很逼真，但其实它们只不过是内部空间很大，且装着一些复杂机械零件的箱子而已。箱子里装着棋盘和棋子，棋子的移动通过一个木偶的手来完成。在下棋之前给我们展示时，箱子里只有一些机器零件，其实它的内部空间很大，完全能够装下一个个子较小的人。

著名的棋手约翰·阿尔盖勒和威廉·刘易斯都曾经饰演过这个角色。当展示箱子的一部分时，藏在里面的人就偷偷地向其他位置移动。所以，这个箱子里面的机械只是道具而已，在下棋的时候，它们并未真的发挥作用。

综上所述，我们能够得出一个结论：棋子间的组合不计其数，并不存在真正的自动下棋机，那些所谓的机器不过是某些机械师骗人的伎俩而已。所以，没有必要对这种所谓的自动下棋机感到恐惧或不可思议。

随着科技的发展，现在我们已经制造出了这种可以自动下棋的机器，这就是计算机，它能在1秒钟的时间里运算几千次，甚至更多。前面我们提到过这种机器，那么，它到底是怎样工作的呢？

其实，计算机所有的工作都建立在运算的基础上，除此以外它什么都不会。但是，我们可以事先编一些程序，让计算机按照一定的步骤进行运算。

数学家就是根据下棋的一些战术来编写程序的。这些战术都是根据走棋的规则制定的，依照这些规则，每个棋子对应的每个位置都有唯一的最佳路线。左边的表格就是一种下棋的战术，其中对每个棋子都规定了一定的分值。

另外，在编写程序时，还按照一定的原则来衡量棋子所处位置的优劣。比如，棋子在中间还是边上，棋子的灵活度如何，等等。位置的优劣也占有一定的分值，通常来说，这个分值不到1分。最后，把白方和黑方的总分相减，所得的差就代表了双方棋局上的优劣。如果是正的，就代表白方占优；如果是负的，则代表黑方占优。

计算机在计算时，通常只计算三步之内的差数，且会判断怎样让这个差数的改变值最大，从而在这三步的所有组合中选择一个最优的方案，并在卡片上打印出来，这就算走完了一步。计算机的运算速度很快，根本不会出现时间不够用的现象。

如果一个机器只能“想出”后面紧跟着的三步棋，它并不能算是一个好的“棋手”。不过，随着计算机技术的发展，计算机“下棋”的技术一定会越来越好。我们在这里不可能详细地描述这类下棋的程序，在下一章中，我们会介绍几个比较简单的运算程序。

用3个2写一个最大的数

【题目】大家肯定都知道如何用3个数写出一个尽可能大的数来。比如，给出3个9，可以写成这样的形式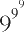：，所得的数就是9的第三级“超乘方”。

那么，这个数到底有多大呢？可以说，根本找不到一个东西来帮我们理解这个数字到底有多大。就算是把宇宙中所有的电子加起来，得到的数字都无法跟这个数相提并论。

下面，我们来看这样一个问题：不使用运算符号，把3个2摆成尽可能大的数。

【解答】有了前面3个9的例子，很多读者第一个想到的肯定是这样的摆法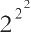：，实际上，得到的结果可能会让你失望，因为它其实并不大，甚至比222还要小很多，它是2 ⁴ ，也就是16。想要用3个2摆成一个最大的数，这个数不是222，也不是22 ² =484，而是2 ²² =4194304。

这个例子很有意思，它说明一个道理：如果用类推法去解决数学问题，很有可能会得到错误的推断。