




接下来,我们研究一下地球公转轨道的形状。地球的运行与其他行星一样,都遵守开普勒第一定律,即行星在椭圆形的公转轨道上运行,太阳位于椭圆的焦点。

图17 在椭圆形中
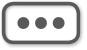
那么,地球公转轨道究竟是一个什么样的椭圆形呢?
在中学的教科书上,我们经常会看到,地球公转轨道被画成一个拉得很长的椭圆形,这让很多人误以为,地球的公转轨道就是一个标准的椭圆形。实际的情况并非如此,地球公转轨道基本上跟圆形差不多,如果画在纸上,你可能会以为它就是一个圆,哪怕把这个轨道的直径画成1米,肉眼看起来依然跟圆形差不多。所以,就算是艺术家那样敏锐的眼睛,也很难区分这种椭圆形和圆形。
如图17所示,这是一个椭圆,AB是椭圆的长径,CD是短径。除了“中心”点O以外,长径AB上还有两个重要的点,被称为“焦点”,它们对于中心点O两边相互对称。在图18中,我们以长径AB的(1/2),即以OB为半径,以短径的端点C为圆心画弧,与长径AB交于点F和点F',那么,这两个点就是椭圆的焦点。这里,OF的长度与OF'相等,通常用c表示,而长径和短径经常用2a和2b表示。c与a的比值,也就是c/a代表椭圆伸长的程度,在几何学上称之为“偏心率”,偏心率越大,椭圆跟圆形的差别越明显。

图18 找出椭圆形焦点F和F'的方法。
可见,倘若我们知道了地球公转轨道的偏心率,就能够确定它的形状。计算偏心率无须知道轨道的大小。我们说过,太阳位于椭圆轨道的一个焦点上,所以,地球公转轨道上的点到太阳的距离都不相等,这就使得太阳看上去时大时小。比如,在7月1日那天,太阳位于图-18的焦点F',而地球位于点A,所以人们看到的太阳最小,如果用角度表示,则是31'28″。到了1月1日,地球位于点B,这时人们看到的太阳最大,如果用角度表示,就是32'32″。由此,可以得出下面的比例关系:

依据上面的比例式,有:

即:

于是又有:

这就是说,地球公转轨道的偏心率是0.017。可见,只要测出太阳的可视圆面,就能确定地球公转轨道的形状。
我们还能用下面的方法验证椭圆轨道和圆形的区别。如果把地球公转轨道画作一个半长径为1米的椭圆,那么,它的短径是多少呢?
利用图18中的直角三角形OCF',可以得出:

两边都除以a 2 :

c/a是地球轨道的偏心率,等于1/60,而a 2 -b 2 =(a+b)(a-b),a和b的差别很小,所以,我们可以用2a来代替(a+b),即把上式简化为:

所以:

这个值小于1/7毫米。
可见,就算是在这么大的一个圆上,这个椭圆轨道的半长径和半短径也只差了不到1/7毫米,比铅笔画的线还要细。所以,就算把轨道画成圆形也没关系。
我们不妨来分析一下,在这张图上,太阳应该在哪儿?前面我们说过,它应该在焦点上,那它距离中心有多远呢?换句话说,图中的OF或OF'有多长呢?我们可以通过计算得出:


图19 假设地球公转轨道比正常情况下扁长许多,且焦点在
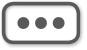
这就是说,太阳在距离轨道中心1.7厘米的地方。如果把太阳的直径画成1厘米,恐怕艺术家也难以发现它是不是处在轨道的中心。
所以,我们画地球公转的轨道时,完全可以把太阳画在轨道的中心,用圆圈来表示。
通过分析我们可知,太阳所处的位置很接近轨道的中心。从严格的意义上讲,如果它真的处在中心位置,会不会影响到气候呢?我们可以深入探讨一下。
假设地球公转轨道的偏心率增加到0.5,即椭圆的焦点刚好平分它的半长径,这时的椭圆会更加扁长,像鸡蛋一样。当然,这里只是做一个假设。实际上,在整个太阳系中,水星轨道的偏心率是最大的,大约是0.25。
如图19所示,假设地球在1月1日时依然位于距离太阳最近的点A,在7月1日时位于距离太阳最远的点B,由于FB是FA的3倍,所以7月1日的太阳到地球的距离将是1月1日的3倍,1月的太阳视直径是7月的3倍。太阳照射到地面的热量与它跟地球的距离平方成反比,所以,1月时地面接受到的热量是7月的9倍。这就是说,在北半球,虽然冬季的太阳高度很低,昼短夜长,但因为距离太阳很近,依然能够接受到更多的热量,所以天气也变得暖和很多。
依据开普勒第二定律,我们知道,在同样的时间里,向量半径扫过的面积是相等的。这里的“向量半径”指的是太阳和行星的连线。当地球围绕太阳公转时,向量半径会不断变化,且在运动时扫过一定的面积。依据开普勒定律,在同样的时间里,这些面积应该是相等的。如图20所示,依据这一原理,想在相同的时间里使扫过的面积相等,那么,地球在运行到距离太阳较近时的速度要比距离太阳较远时的速度快一些,因为向量半径小一些。
在前面的假设下,每年的12月到第二年的2月,由于地球距离太阳很近,它运行的速度应该比6月到8月快。也就是说,在北半球,冬天将过得很快,且夏天会变得很长,这样地面接受到的热量会更多。
由此,我们可得出图21所示的季节长短图。
图中的椭圆形是假定偏心率为0.5时的地球公转轨道。为了便于分析,我们把轨道划分为12段,分别用数字1~12标记,每一段表示地球在相等时间内运行的路程。依据开普勒定律,这12块面积应该相等,因为这12个点与太阳的连线是向量半径。比如,1月1日,地球在点1;2月1日,地球在点2;3月1日,地球在点3,以此类推。这样就很容易得出,春分(A)会在2月上旬出现,秋分(B)会推到11月下旬。也就是说,在北半球,冬季将从12月底开始,第二年的2月初就结束,前后只有1个多月的时间,在从春分到秋分的9个半月时间里,昼长夜短,太阳距离地球也比较远。

图20 开普勒第二定律:如果弧线AB、CD、EF是行星
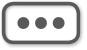

图21 假设地球公转轨道变得更扁长,季节长短也会发生变
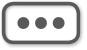
如果是南半球,情况就不同了。在昼短夜长、太阳位置较低时,太阳距离地球较远,所以地面接受到的热量很少,只有地球离太阳较近时的1/9。但是,在昼长夜短、太阳位置较高时,地面接受到的热量是地球距离太阳较远时的9倍。也就是说,在南半球,冬季比北半球更长、更冷,而夏天则更短、更热。
在这个假设下,还会产生另一个结果。由于1月时地球运行得很快,所以,真正中午跟平均中午之间会差很多,有时甚至会差几个小时。对我们来说,这会严重影响我们的作息。
可见,在前面的假设下,太阳“偏心”位置不同,影响也不一样:在北半球,冬季比南半球更短、更暖,而夏季刚好相反。实际上,我们每个人都会观察到这样的现象。在1月的时候,地球到太阳的距离比7月近了2×1/60=1/30,1月份地球接受到太阳的热量是7月的
 倍,也就是比7月多了7%左右。所以,北半球的冬天相对暖和一些。
倍,也就是比7月多了7%左右。所以,北半球的冬天相对暖和一些。
另外,在北半球,秋季和冬季的天数加起来要比南半球少8天,而春季和夏季的天数加起来则比南半球要多8天,这大概就是南极上的冰雪比北半球多一半的原因吧。在下面的表中,我们列出了南北半球四季的时间。

显而易见,北半球的夏季比冬季多了4.6天,春季比秋季多了3天。但是,由于天体空间中地球轨道的长径不断变化,导致轨道上距离太阳最远和最近的点也不停变化,所以,北半球的这个优势也会变化。有人计算过,大概每过21000年,这个变化会重新来一次,从公元10700年开始,这一优势将会转移到南半球。
实际上,地球公转轨道的偏心率的确在逐渐发生变化,从接近圆形的0.003变成像火星轨道那样的0.077。目前,地球公转轨道的偏心率在逐渐变小,大概24000年后,将会缩小到0.003,在接下来的40000年里,又会逐渐变大。当然,我们的讨论现在也只是存在于理论中,没有任何的实际意义。