




《义务教育数学课程标准(2011年版)》(以下简称“课标(2011年版)”)第一学段和第二学段分别列入了“探索规律”的课程内容,其中第一学段对这一内容给出的解释为“探索简单情境下的变化规律”,第二学段的解释为“探索给定情境中隐含的规律或变化趋势”。这些说法尚显笼统、宽泛。需要进一步搞清楚的问题是:这里所说的情境具有什么特点?其中的“规律”是什么意思?“探索规律”指的是什么样的学习活动?
为了理解这里所说“规律”的含义,先来分析“课标(2011年版)”中给出的例题。针对“探索规律”这一课程内容,“课标(2011年版)”中一共出现了4道例题,其中第一学段中共有2道(在“课标(2011年版)”中为例9和例10),见例题2-1和例题2-2。
在下列横线上填上合适的数字、字母或图形,并说明理由。
1,1,2;1,1,2;______,______,______;
A,A,B;A,A,B;______,______,______;
 ,
,
 ,
,
 ;
;
 ,
,
 ,
,
 ;______,______,______;
;______,______,______;
在图2-1中,描出横排和竖排上两个数相加等于10的格子,再分别描出相加等于6,9的格子,你能发现什么规律?
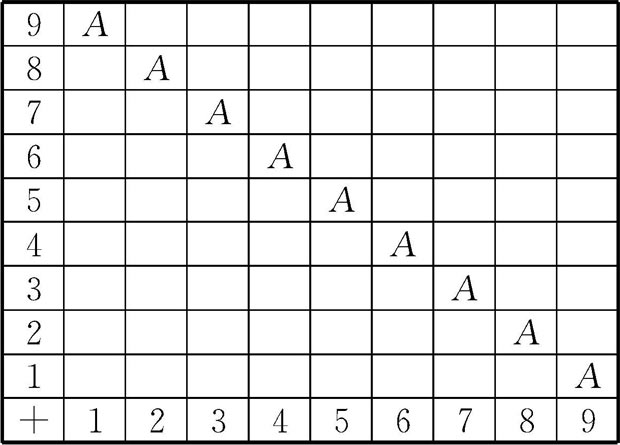
图2-1
例题2-1所给出情境的特点是多个对象(数字,字母,图形)有序排列,并且按照确定的个数3重复出现,构成循环,学生发现这样的规律后就可以预见后面相应位置的情况了。例题2-2的特点是相加为10的格子涂色后,恰好构成了自左上到右下的“对角线”图案(图2-1中字母A处)。
“课标(2011年版)”第二学段课程内容中关于“探索规律”的2道例题分别是例30和例31,本书此处见例题2-3和2-4。
联欢会上,小明按照3个红气球、2个黄气球、1个绿气球的顺序把气球串起来装饰教室。你知道第16个气球是什么颜色吗?
一个房间里有4条腿的椅子和3条腿的凳子共16个,如果椅子腿数和凳子腿数共60条,那么有几个椅子和几个凳子?
例题2-3所描述情境的特点与前面例2-1是类似的,仍然是多个对象有序排列,并且按照固定个数重复出现,体现的是循环的规律。例题2-4从表面看不具备前面例题中“有序排列”和“图案”的特征,但可以用下面的表格(表2-1)将问题情境改造为“有序排列”的表述方式:
表2-1 情境改造表

表2-1第一行表达出椅子个数依次递增的有序排列,第二行表示凳子个数依次递减的有序排列,第三行则显现出总腿数“每个数比前一个数多1”的排列规律。
从上面4道例题可以发现,这里所说的规律指的是运动或变化过程中的不变因素,这样的不变因素将不同对象或同一对象的不同运动状态联系起来,进而使得这种运动或变化状态和趋势可以把握。简单说,所谓规律就是“变中的不变”,比如前面的例题2-3的表2-1中,随着椅子和凳子个数的不断变化,总腿数从48开始也在不断变化,在这个变化过程中,对应的椅子个数和凳子个数的和(16)是确定不变的,进而导致总腿数每次增加1也是不变的,正是这样的规律使得椅子个数、凳子个数以及总腿数之间建立了联系,进而使得它们的变化状态和趋势可以把握了。
与这一含义较为接近的英文单词应该是“pattern”,这一单词在英汉词典中通常译为“模式”。《麦克米伦高阶英语词典》针对“pattern”的第一条释义为:“一系列行为或事件,共同展示了事物是如何规范地发生与发展的。”与这里所说的“规律”的含义基本一致。因此,所谓探索规律的一个重要内容就是在运动与变化过程中寻找不变因素,在国外许多教科书中把这样的内容叫做“发现规律(finding pattern)”,就是我们通常所说的“探索规律”。
“发现”作为人类的认识活动,要基于客观存在和主观意愿的共同作用。这种主观意愿主要包括两方面,第一是相信规律的存在,第二是有把握事物及其变化的意愿或动机。在此基础上,通过对个别、具体对象及其关系的观察和比较,找到能够制约这些对象及其关系的确定性因素,进而通过归纳和解释确定具有普遍性的规律,之后根据情况对这样的规律进行推广和应用。
如果把“发现规律”看作是学生的学习活动,那么这样的学习活动一般来说起码应当包括六个环节。一是建立“目标和动机”,这一环节的目的是让学习者明确“我想要做什么”或者“我需要做什么”,为后面的活动明确目标,形成动机。二是明确“情境与对象”,这个环节具有承上启下的作用,一方面可以帮助学生回忆已有的相关知识和经验,另一方面建立后面活动的观察对象。三是针对相关情境或研究对象的“观察与比较”,这是发现规律的核心环节,不仅需要观察对象本身,更需要把注意力放在对象之间的关系方面;四是对初步结论的“归纳与解释”,通过观察与比较,可能会得到一些相对零散的结论或者猜想,这时就需要找到他们的共性,归纳出具有一定普遍性的结论或者猜想,而后对这样的结论或者猜想的正确性进行解释和验证。五是对所得结论的“推广或应用”,任何一个规律往往会孕育着更具普遍性的规律,同时发现了规律往往意味着很多相关问题可以得到解释,因此这个环节的目的在于培养学生推广与应用的意识。六是对发现过程和结论的“反思和总结”,发现规律的过程中会生成很多想法,把这些想法及时总结并固化为文字,这样的过程可以培养学生及时反思和总结的习惯,同时逐步培养学生用语言表达自己想法的能力。下面用一个实际例子说明这样的过程。
20世纪末期曾经出现了一个世界范围的困惑与争论:即将来临的21世纪的第一年应当是2000年,还是2001年?

要想回答这个问题,自然应当把公元纪年的规律搞清楚。首先需要明确两个前提。第一,公元纪年起始年为公元1年或元年,也就是没有公元0年;第二,一个世纪规定为100年。为了便于观察和比较,可以把从公元元年开始的纪年方式有序地排列出来:

图2-2 公元纪年图示
观察图2-2,纵向看公元1世纪最后一年是公元100年,公元2世纪最后一年是公元200年,依此类推可以得到初步结论:“公元n世纪最后一年的年数是n×100。”据此就可以初步得到结论,21世纪最后一年是2100年,因此倒推100年得到21世纪第一年是2001年。
横向看相邻两个世纪对应年数相差100,比如公元3世纪第一年201比公元2世纪第一年101多100。由此推断出21世纪第一年应当比1多20个100,因此21世纪第一年应当是2001年。也可以先求出20世纪最后一年是2000年,进而得到21世纪第一年是2001年,这样就进一步验证了结论的正确。运用同样的规律可以知道公元22世纪的第一年是2101年等等。如果把以上内容设计成一节课的教学方案(简称“教案”),则可以用如下表格(表2-2)的方式呈现。
表2-2 例题2-5的教案
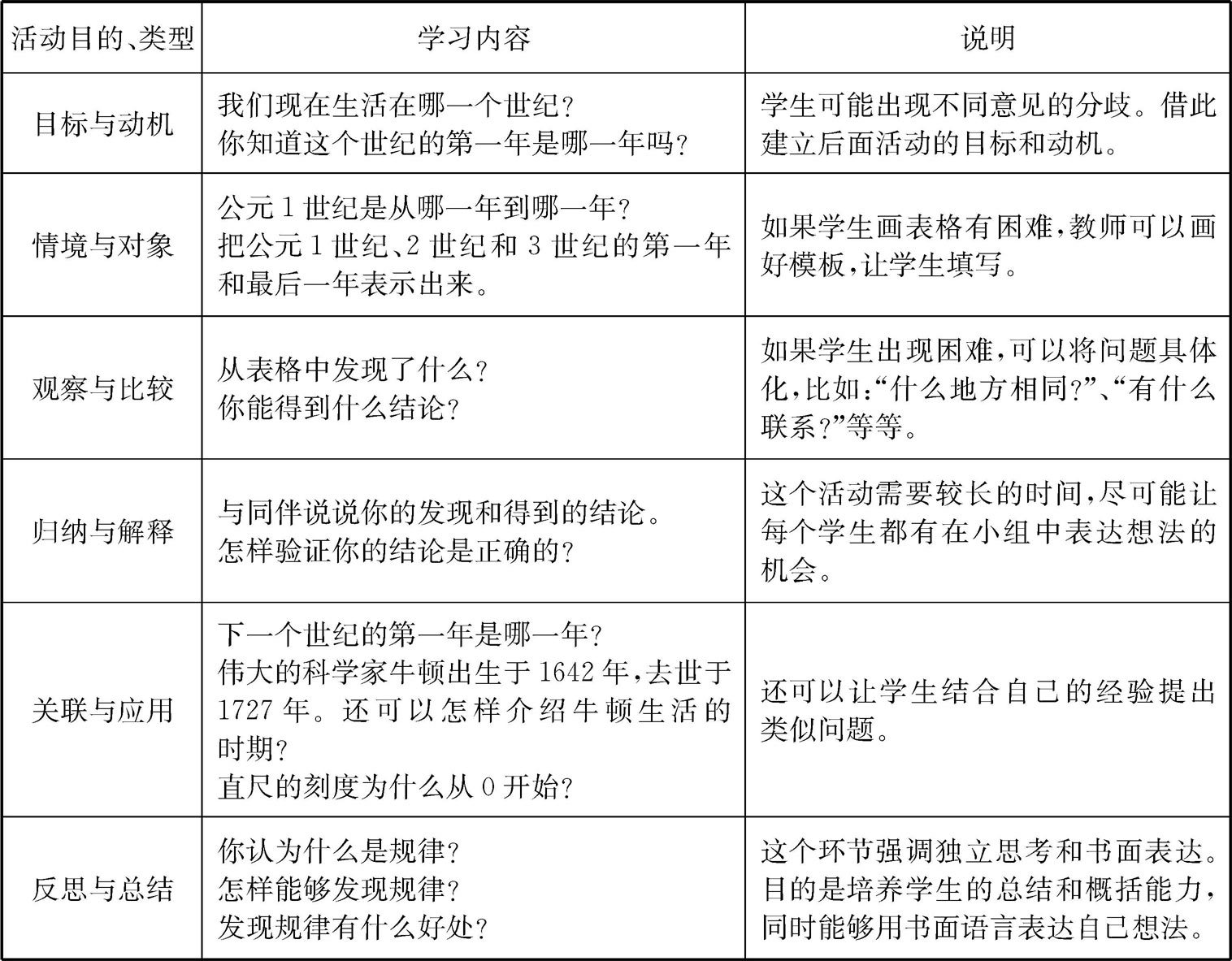
以上学习过程的核心环节是“观察”,观察的重点特别要关注对象之间的关系,这种关系往往体现为“变化过程中的不变因素”。这样的学习活动设计应当说突出了规律的本质。除此之外,学习活动的设计中还应当重视渗透文化和关联思考。比如表2-2中关于牛顿生卒时间的问题以及直尺刻度的问题设计,都是出于这种考虑。
广义的规律指的是事物之间必然的联系,这样的联系大致说有两种类型。一种是前面所说的“运动与变化过程中的不变因素”,需要通过观察和比较去发现,不妨叫做“显性的规律”。还有一种事物之间的联系体现为“原因和结果”或“本质与现象”之间依赖与制约的关系。通过观察与比较往往发现的是“结果”或“现象”这样显性的内容,探索规律还应当包括揭示产生结果的“原因”,或导致现象发生的“本质”。这样的规律可以称之为“隐性的规律”。下面用小学数学课程中“数的整除特征”为例进行说明。
“2,3,5的整除特征”通常是小学五年级的课程内容。其教学过程大致来说是通过观察和比较一些具体特例,找到“变化中的不变因素”,而后归纳出结论。以“5的整除特征”为例,人民教育出版社出版的义务教育课程标准实验教科书《数学(五年级下册)》关于这一内容的安排为,先在1—100的数表中找到“5”的倍数,然后发现其个位数字都是“5”或“0”,因此得到“个位数字为5或0的数是5的倍数”的结论(见图2-3)。
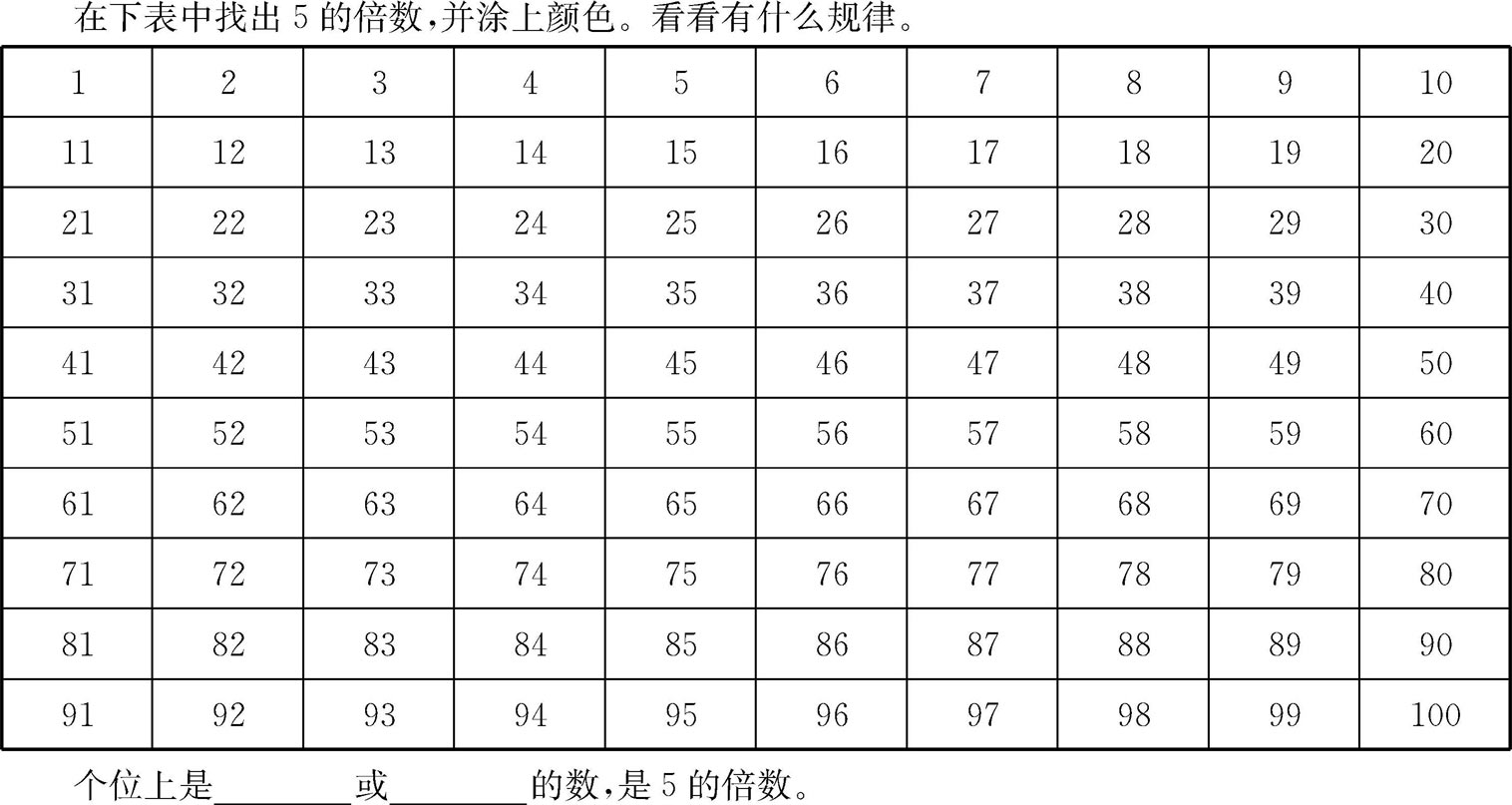
图2-3 人教版教科书“5的整除特征”扫描图
这样的设计存在两个问题,第一个问题是从特例中归纳(实际上是“不完全归纳”)出的结论应当是“如果一个数是5的倍数,那么其个位数字是5或0”,而不是其逆命题“如果一个数的个位数字是5或0,那么这个数是5的倍数。”第二个问题是没有引发学生去进一步探索隐性的规律,也就是5的倍数具有这种特征的原因是什么?为什么5和2具有相同的整除特征?
事实上,任何一个正整数都可以写成一个10的倍数与其个位数字之和的形式,比如“84”可以写成“8×10+4”,“2015”可以写成“201×10+5”等等。而“10”是“5”的倍数,因此这个数是否是“5”的倍数就由个位数字决定了。同样道理,“10”同时也是2的倍数,所以“2”和“5”的整除特征是一样的。这样的内容还能为中学数学和物理中的“科学记数法”做铺垫,所谓“科学记数法”就是把一个多位数,比如n+1位数“
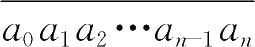 ”写成如下的形式:
”写成如下的形式:
a 0 ×10 n +a 1 ×10 n-1 +a 2 ×10 n-2 +…+a n-1 ×10 1 +a n ×10 0 [2]
基于以上分析,为了引导学生用“探索规律”的过程学习“数的整除特征”这一内容,可以将“2”和“5”的整除特征放在一起同时学习,为此设计如下的教学方案表2-3。
表2-3 “2”和“5”整除特征教案
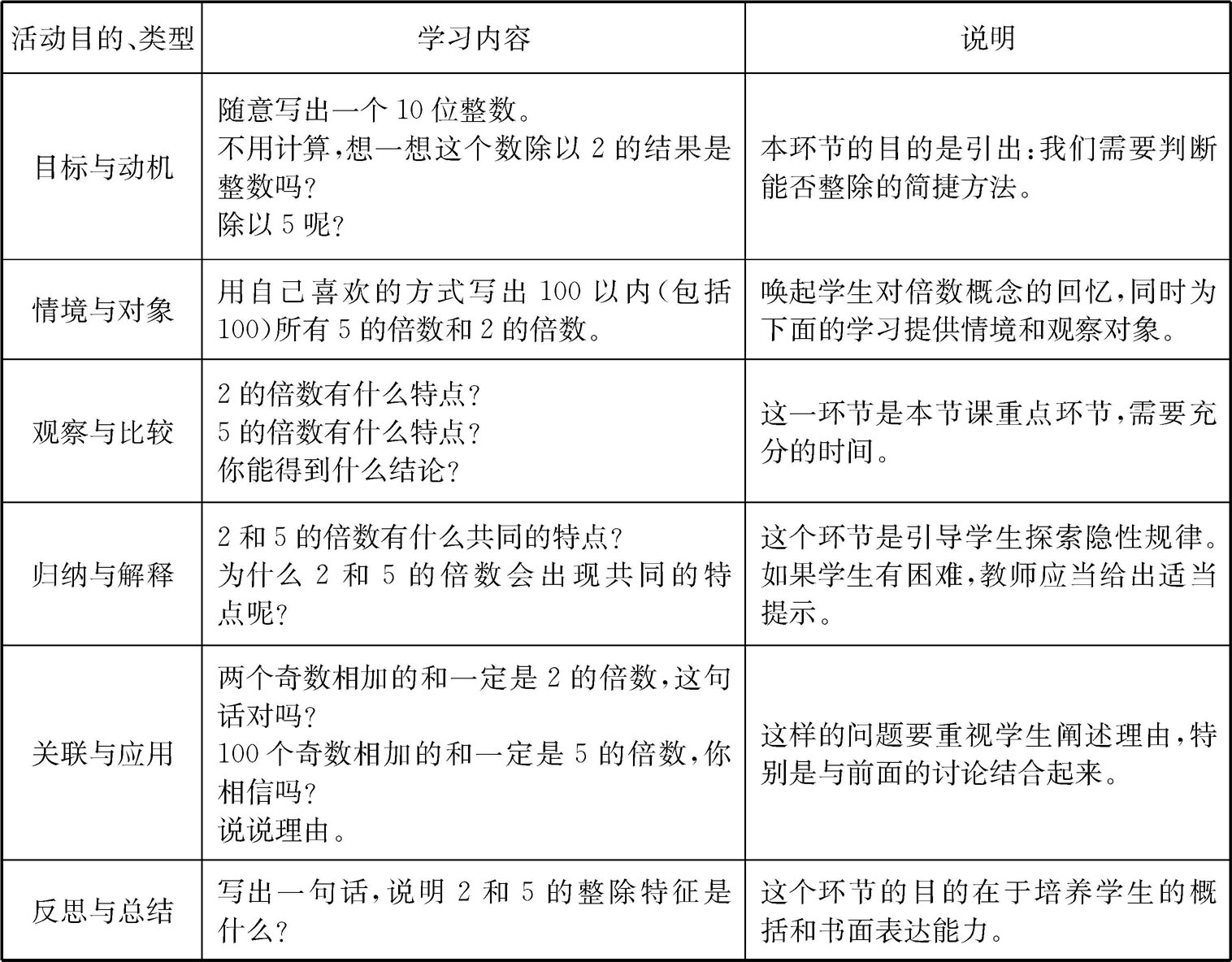
这个教学设计与前面“发现规律”的设计框架是一样的,其中对隐性规律的探索体现于“归纳与解释”这个环节中了。
“课标(2011年版)”以及教科书是将“探索规律”与诸如数的认识、数的运算以及常见的量并列为课程内容,这可能是想突出这一内容的重要性。事实上,个人建议把探索规律看作人的认识活动以及学生的学习活动,应当贯穿于整个数学学习的过程中。
[2]
还可以写成更简单的形式“
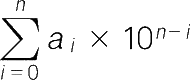 ”。
”。