




在16个小方格中先给定了若干个1~4之内的数字,称为数独的谜题,如图1-2所示。谜题中给出6个已知数2、1、4、2、2、3,解题时还需要在空格中填上10个数字,使四字数独中的每行、每列、每个四宫格中都有1~4的数字。也就是说,在每行、每列、每个四宫格中只能出现1~4之内的1个数字,每个数字只能出现1次,不能重复,也不能缺少,而且答案是唯一的,如图1-3所示。
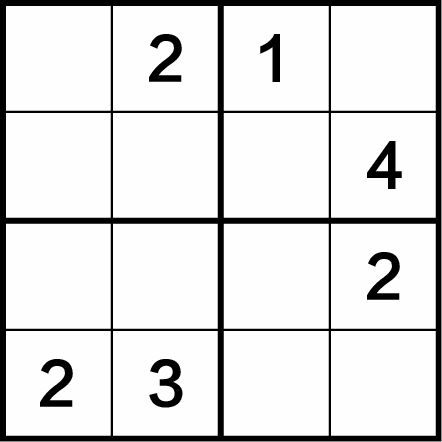
图1-2
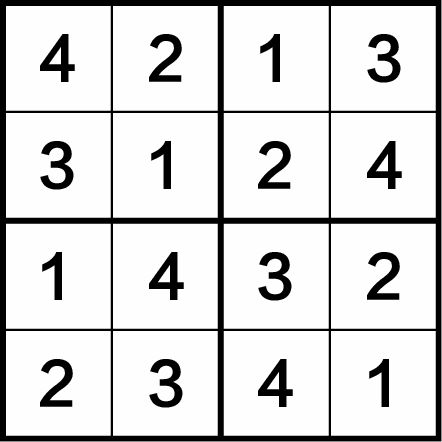
图1-3
这是一种最简单、最直接的解题方法,就是在每行或每列中已给出3个数字,还缺1个数字。根据数独的性质,只要把所缺的数字填上,使每行、每列中的数字1~4不重复即可。由图1-4可看出,该谜题的第一行、第二行、第三列都是“四缺一”。解题步骤如下。
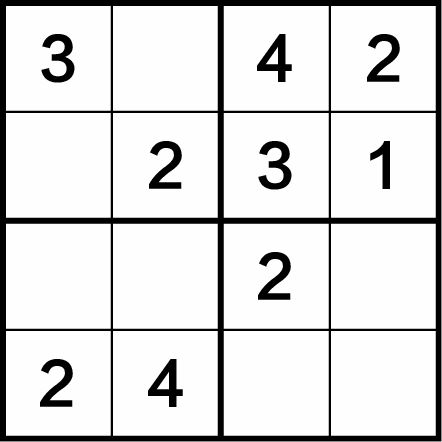
图1-4
第一步:如图1-5(a)所示,用画直线的方法来表示某行、某列是“四缺一”,再用画圆圈的方法来表示该行或该列所缺的数字,这样就很容易找到(1,2)格中应填入数字1,(2,1)格中应填入数字4,(4,3)格中应填入数字1。
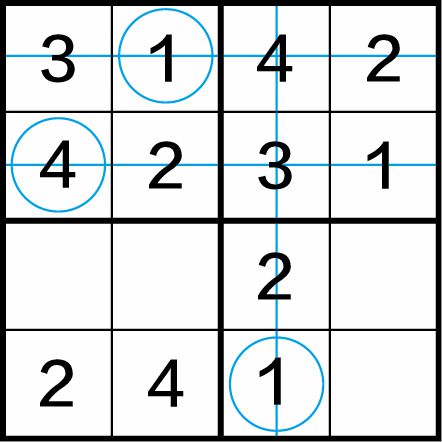
图1-5(a)
第二步:如图1-5(b)所示,在第四行、第一列、第二列中又是“四缺一”,用圆圈表示尚需填入的数字,(4,4)格中应填入数字3,(3,1)格、(3,2)格中应分别填入数字1和3。
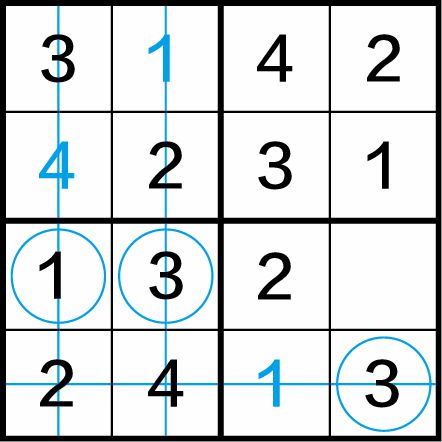
图1-5(b)
第三步:在图1-5(c)中,(3,4)格是待填数字的空格,仍用圆圈表示,这也是“四缺一”。该小格中应填入数字4,至此就得到了最后的解题结果。
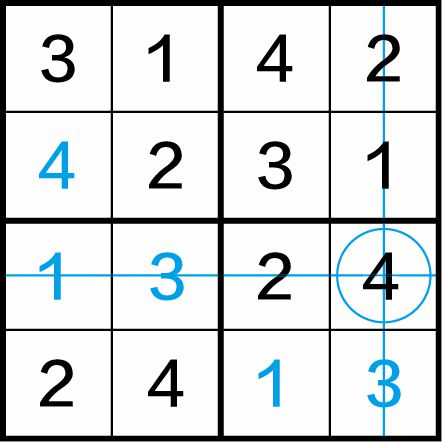
图1-5(c)
四宫格“四缺一”法与上述解题方法相似,是一个四宫格中已知3个数字,只缺1个数字待填。如图1-6所示,该谜题中已给出8个数字,还有8个空格需要填入相应的数字,解题步骤如下。
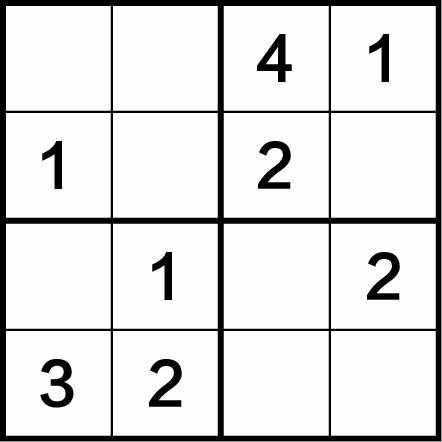
图1-6
第一步:图1-7(a)中,在左下的四宫格的圆圈中应填入数字4,在右上四宫格的圆圈中应填入数字3。
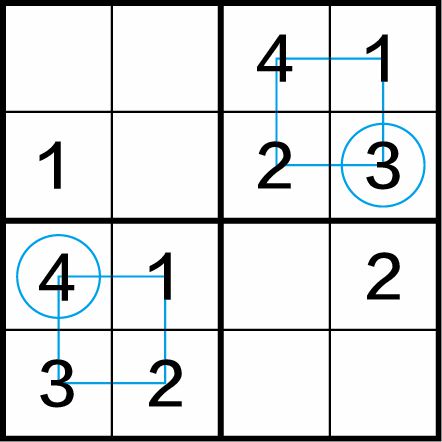
图1-7(a)
第二步:图1-7(b)中,第二行、第三行都是“四缺一”,因此,(2,2)格中应填入数字4,(3,3)格中应填入数字3。
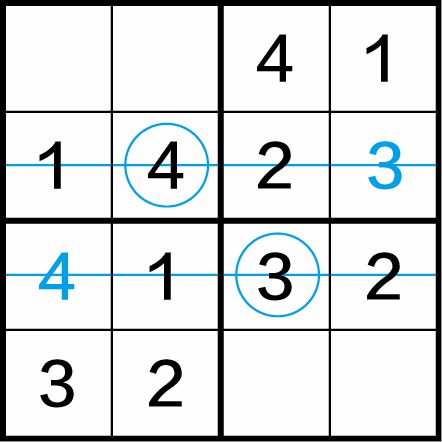
图1-7(b)
第三步:图1-7(c)中,第一、第二、第三、第四列中都是“四缺一”。应分别填入数字2、3、1、4,得到最终结果。
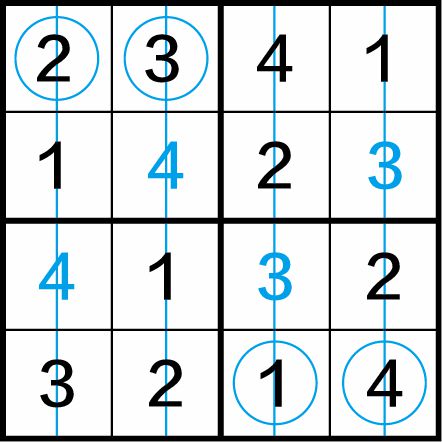
图1-7(c)
由此可知,在这道题的整个解题过程中,不仅使用了某个四宫格“四缺一”的解题方法,而且同时应用了某行或某列“四缺一”的解题方法。
在图1-8的四字数独中,已填有6个数字4、3、2、3、4、2,待填入的数字有10个。在每一行、每一列、每一个四宫格中最多只有2个数字,显然,在此谜题中不能运用“四缺一”的解题方法来解题。此时,可应用“二筛一”的筛选方法进行解题,即从2个空缺的数字中筛去一个。解题步骤和方法如下。
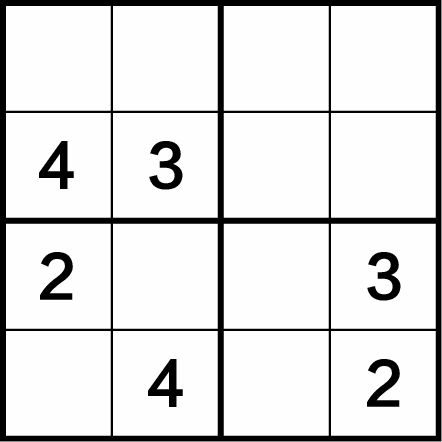
图1-8
第一步:如图1-9(a)所示,在第二列中已有数字3和4,还缺2个数字1和2。那么如何选择呢?看第三行,(3,1)格已有数字2,则(3,2)格中不能填入数字2,只能填入数字1,所以数字2只能填入(2,1)格中。
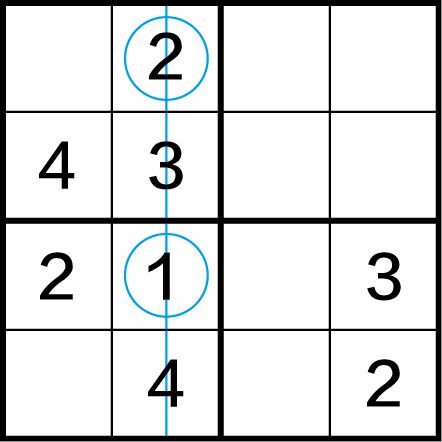
图1-9(a)
第二步:再利用四宫格“四缺一”的方法,得到(1,1)格中应填入数字1,(1,4)格中应填入数字3,如图1-9(b)所示。
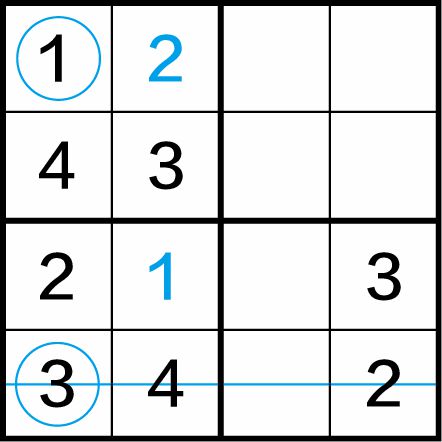
图1-9(b)
第三步:利用行“四缺一”法,得到(3,3)格中应填入数字4,(4,3)格中应填入数字1,如图1-9(c)所示。
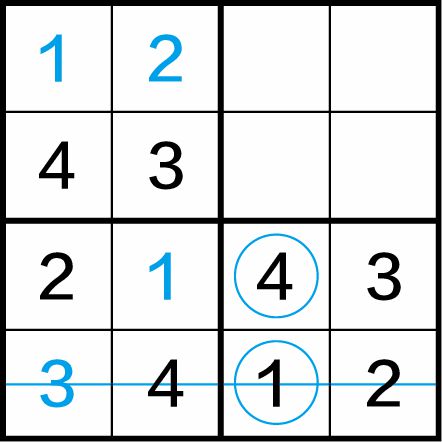
图1-9(c)
第四步:最后利用“二筛一”法,由于第三列中有数字4,第四列中有数字3,则(1,3)格中应填入数字3,(1,4)格中应填入4。同理,由于第三列中有数字1,第四列中有数字2,所以,在(2,3)格中应填入数字2,(2,4)格中应填入数字1。其结果如图1-9(d)所示。
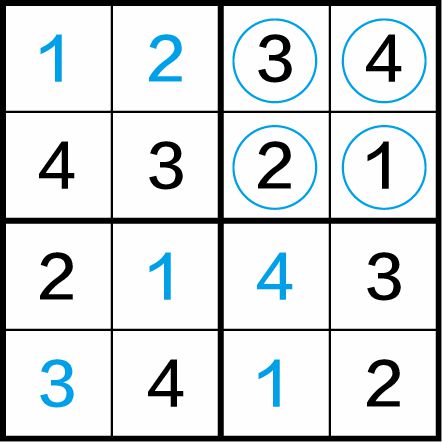
图1-9(d)
如图1-10所示,在此数独中只填有4个数字3、4、1、2,还缺12个数字。初看起来,似乎很难求解。难解的原因是每一行、每一列及每个2×2的四宫格中都只有1个数字,尚缺3个数字。解这一类数独可采用“三筛二”法,具体解题步骤如下。
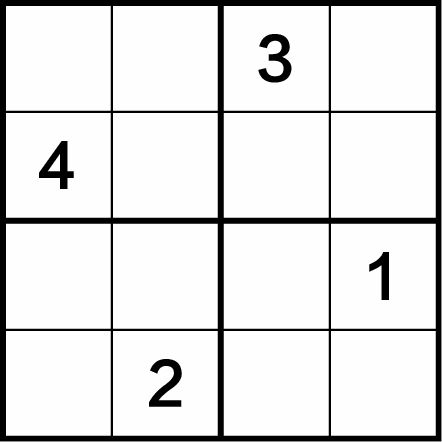
图1-10
第一步:先看第三行(当然,先看其他行也可以),已有数字1,尚缺2、3、4,但在左下方的四宫格中已有2,所以(3,1)格、(3,2)格中不能填入数字2,只能在(3,3)格中填入数字2,如图1-11(a)所示。
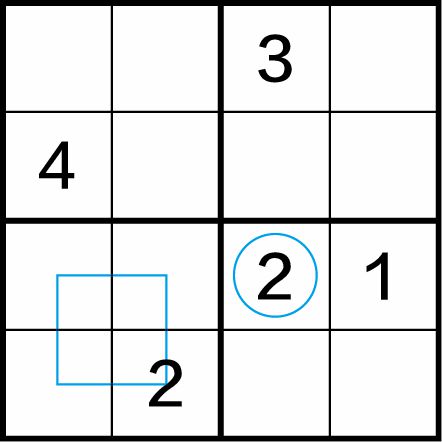
图1-11(a)
第二步:至此,在第三行中已有数字2和1,尚缺3和4,由于在第一列中已有数字4,采用“二筛一”法来解题,得到(3,1)格中应填入数字3,(3,2)格中应填入数字4。此时,再来看左下方的四宫格,在(4,1)格中应填入数字1。接着看第一列是“四缺一”,则(1,1)格中应填入数字2,如图1-11(b)所示。
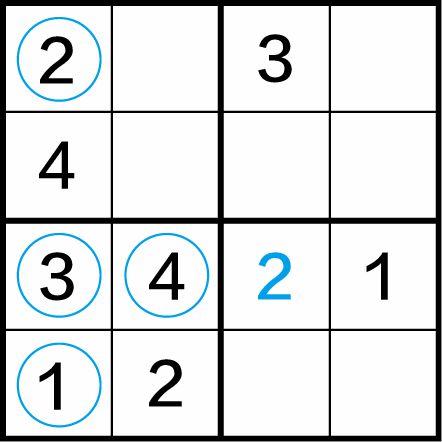
图1-11(b)
第三步:再来看第一、第四行,在这两行中可以采用“二筛一”法,从空缺的2个小方格中筛去1个数字。在第一行中缺1和4,但在第四列中已有数字1,所以(1,4)格中不能填入1,而应填入4,则在(1,2)格中应填入1。同理,在第四行中已有数字1和2,尚缺3和4,因在第一行的第3、第4个小方格中分别有3和4,所以,在(4,3)格中应填入数字4,(4,4)格中应填入数字3,如图1-11(c)所示。
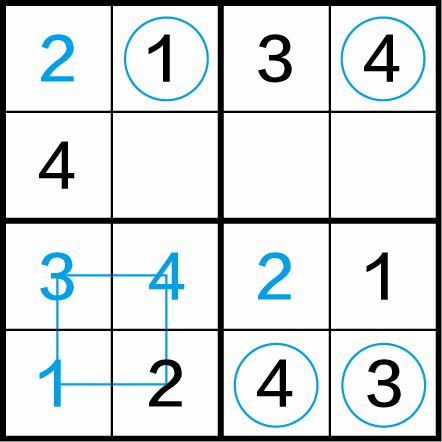
图1-11(c)
第四步:看图1-11(d),在第二、第三和第四列中,都只有3个数字,应用“四缺一”法,得到(2,2)格中应填入3,(2,3)格中应填入数字1,(2,4)格中应填入数字2,得到最终结果。
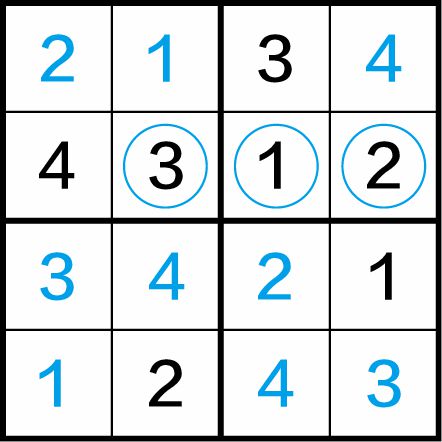
图1-11(d)
如图1-12所示,在此数独中,只有4个数字2、1、4、3,还有12个空格需要填入数字。初看起来,此题似乎也很难求解。我们现在学习“排除法”来解题,解题步骤如下。
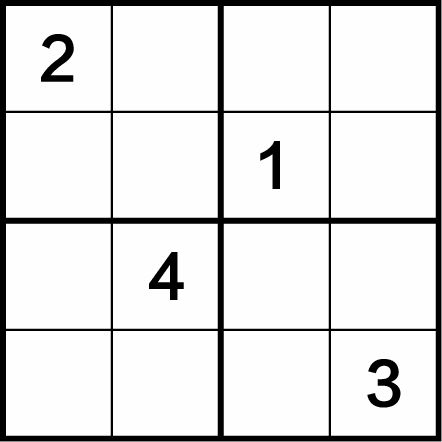
图1-12
第一步:先看第一、第二行,因为(4,4)格中已有数字3,则(1,4)格、(2,4)格中不能填入3,所以右上四宫格(1,3)格中应填入数字3。同理,(2,1)格中只能填入数字4;(3,4)格中只能填入数字1;(4,2)格中只能填入数字2,如图1-13(a)。
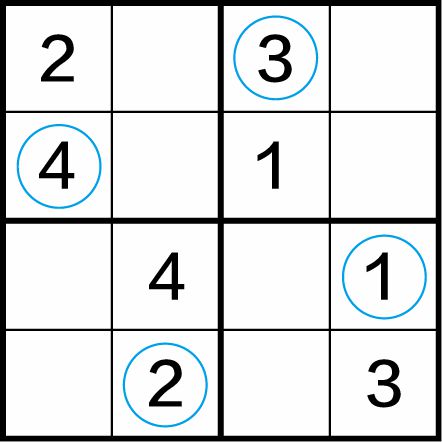
图1-13(a)
第二步:继续使用“排除法”,得到(3,1)格、(4,1)格中应分别填入数字3和1;(2,2)格、(2,4)格中应分别填入数字3和2,如图1-13(b)所示。
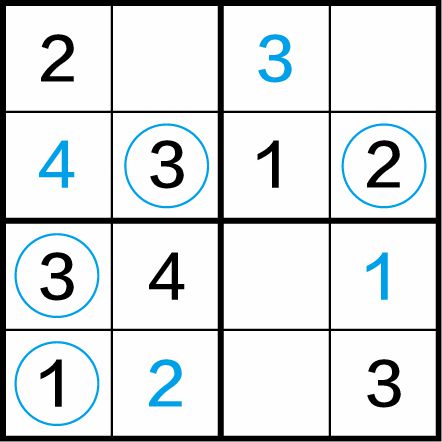
图1-13(b)
第三步:利用“四缺一”法,得到最终答案,如图1-13(c)所示。
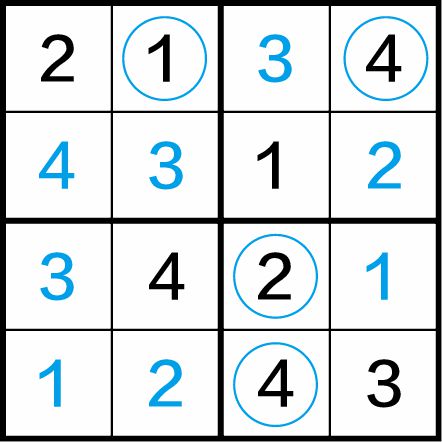
图1-13(c)