





计算流体力学(computational fluid dynamics,简称CFD)是以计算机数值计算为基础,对流体流动、传热以及反应等相关现象进行分析的一种研究方法 [22~24] 。CFD的基本思想是把原来在空间及时空上连续的物理场(如速度场),用有限个离散点变量值的集合来替代,通过一定原则和方式创建关于这些离散点场变量之间关系的代数方程组,然后求解这些代数方程组获得场变量的近似解。随着对CFD的深入研究,其准确性、可靠性、计算效率等都得到大幅提高,已经从简单的定性分析发展到定量计算,可以部分或完全代替实验装置;其在新工艺、新设备的开发、设计、改造中应用愈来愈广泛。尽管一般情况下计算方法并不能完全取代实验测试,但对实验的依赖可显著降低。通过数值模拟,不仅可以充分认识流动规律,方便评价、选择多个设计方案,进行优化设计,还可以大幅度减少实验和测试等试验研究的工作量。在降低设计成本、缩短开发周期以及提高自主研发能力等方面起到了非常重要的作用。
为实现对CFD数值计算的自动化、可视化,CFD数值计算方法已经软件化。目前,常用的CFD软件有PHOE-NICS、FLUENT、STAR.CD、CFX、POLYFLOW等。其中FLUENT软件是目前应用最为广泛的CFD计算软件 [25] 。FLUENT自1983年问世以来,被广泛应用于航空航天、航海、材料、冶金、石油化工、汽车、能源、生物、医药等领域。FLUENT软件包含了基于密度的隐式求解器、基于密度的显示求解器、基于压力的分离求解器和基于压力的耦合求解器。多求解器技术使FLUENT软件可以用来模拟从不可压缩到高超音速范围内的各种复杂流场,而且FLUENT软件中包含了很多经过工程确认的物理模型,可以较为准确地模拟高超音速流场、传热与相变、化学反应与燃烧、多相流、旋转机械、动/变形网格、噪声、材料加工等复杂机理的流动问题。
CFD软件由前处理、求解器和后处理三部分组成。前处理、求解器及后处理三大模块,各有其独特的作用。前处理的主要功能是创建所要求解模型的几何结构并进行网格划分,并为解算器定义需要解决问题的参数。主要内容包括:建立模型(1D、2D、3D),网格划分,定义物性参数,设置边界条件。数值模拟的求解是在网格基础上进行的,故网格愈多计算结果愈精确,但同时也对计算机提出了更高的要求,所以网格的数量应综合考虑计算精度需求与计算量来确定。求解器的任务是求解一系列的方程,是流体计算的核心部分。现有的求解方法主要有三种:有限差分法、有限元法和有限体积法。FLUENT软件采用有限体积法对控制方程进行离散,即类似于控制容积法来离散方程,因而可以保证数值计算结果的守恒特性。后处理用于从各个方面观察流体计算结果和输出数据。它主要包括:计算域与网格的显示、速度和压力等矢量图、等值线图、云图等。
CFD是对流体流动、传热以及反应等相关现象进行分析的一种研究方法,而对流体流动与传热进行描述的基本定律包括质量守恒定律、动量守恒定律和能量守恒定律。对于含有不同成分的反应体系还应遵循组分守恒定律。以上这些守恒方程的数学描述便是控制方程组。在进行数值计算分析时,控制方程可经过适当的数学处理化为通用微分方程 [26] ,具体形式如下:
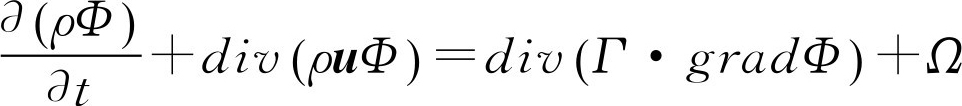
Φ 为通用变量,可以表示速度矢量、温度、组分浓度等变量。公式中各项依次表示瞬态项、对流项、扩散项和源项。对于不同的控制方程, Φ 、 Γ 和 Ω 所对应的形式也有所不同,具体对应关系如表1.2所示。
表1.2 通用控制方程中各符号的具体形式

一般来讲,工程燃烧装置内的流动都是湍流流动。湍流是一种非常复杂的非稳态三维多尺度流动。湍流中流体的各种物理量,如速度、压力、密度和温度等都随时间与空间发生随机的变化。描述湍流的基本方程就是非定常三维Navier-Stokes方程。目前,对于湍流的处理主要有三种方式,它们分别是:直接模拟(direct numerical simulation,DNS)、大涡模拟(large eddy simulation,LES)和雷诺平均法(Reynoldaaveraged Navier-Stokes,RANS) [27~29] 。第一种方法为直接数值模拟(DNS),即直接求解非定常的Navier-Stokes方程。由于湍流含有极小的时间、空间尺度,因此必须采用非常小的时间与空间步长,从而对计算机CPU速度及内存提出了极高的要求。目前,DNS仅限于分析一些几何形状较为简单的理论问题,对于实际工程装置内的流动问题,在近期内尚难以实现DNS计算。另一种仅次于DNS的数值模拟是大涡模拟(LES),其基本思想是对大尺度涡直接求解N-S方程,对小尺度涡则采用湍流封闭模型,从而获得封闭方程组。LES可以模拟湍流发展过程的一些细节,其计算量较DNS小了许多,但仍大得难以用于解决工程实际问题。目前工程中常用的是第三种方法,即采用Reynolds(雷诺)平均Navier-Stokes方程,其中的雷诺应力,用湍流模型进行模拟。这种方法的计算量远小于前两种,获得了广泛的应用。
近年来,湍流模型的研究是一个十分活跃的课题。除常见的零方程、一方程、两方程模型外,针对各种特定条件的湍流模型不断出现,它们各有各的优缺点。但迄今为止,尚无一种模型可以适用各种湍流。最常用的湍流模型有标准模型、RNG模型、带旋流修正的Realizable模型和雷诺应力模型 [30~32] 。
标准模型属于双方程模型,已经广泛应用二十年以上,它是基于漩涡黏度各向同性假设上的半经验模型。该方法首先求解湍动能 k 方程和湍流耗散率 ε 方程,之后将计算所得 k / ε 的值代入湍流黏度公式,计算黏度,最后依据Boussinesq假设获得雷诺应力解。标准模型假定流场是充分发展的湍流,忽略了流体分子之间的黏性,因此,标准模型只适用于完全湍流的流场。
RNG模型是由瞬态N-S方程进行数学推导而来的,解析性也由标准模型推导而来,其与标准模型的主要区别在于以下几点。
①标准模型是以传统的雷诺平均为基础而得到的,而RNG模型是通过更加精确的统计方法得到。
②在RNG模型中, ε 方程内有一项专门考虑了快速变形流动的影响,所以对于快速变形流动来说,该模型的预测更加准确。
③RNG模型中包含了湍流中漩涡的影响,可以在一定程度上提高涡旋流预测的准确性。
④标准模型中,湍流流动Prandt数是一个常数,而RNG模型同时考虑了低雷诺数和高雷诺数的影响,所以也适用于低雷诺数流体的模拟。
所有上面所列的这些特点使得RNG模型比标准模型更加准确和可靠,它特别适用于模拟以下这些流动方式:分层流、环流、在弯曲几何体里的流动、快速变形的流动、剪切层不稳定的流动、涡旋流、低Prandt数流体的传热、低雷诺数流体流动或过渡流。但是,在旋转坐标系中,RNG模型的预测结果是否正确,还需进一步验证。
Realizable模型与标准模型、RNG模型的不同之处主要体现在 ε 方程上,在该模型 ε 方程中产生的一项没有包含在 k 方程中。另外,Realizaable模型与标准模型、RNG模型在对涡流黏度的表达方式上也不相同,各自的能量耗散方程也不同。通过一系列的理论和实验验证,带旋流修正的Realizable模型与RNG模型的适用范围具有很多相似点,不但适用于靠近壁面处流体的流动、具有高度弯曲流线的流体流动、低雷诺数情况下的流体流动、尾流和漩涡流等,而且也适用于在旋转坐标系下非均相的剪切流、靠近边界层的流体流动等。
雷诺应力模型(Reynoldss tress model,RSM)是现阶段较先进的模型,它不再使用Boussinesq中关于湍流动力黏度各向同性、时均速度梯度与湍流应力呈线性关系的假设,因而它对各向异性的不均匀湍流运动的模拟显示出了不可比拟的优势。同时也考虑了流体旋转流动以及流动方向改变对整体流场的影响。该模型本身含有11个未知参数,即需要求解11个多参数方程,而且该模型中有14个经验系数,这些系数确定起来较为困难。近年来,该模型已经在尝试用于预测燃烧室及燃烧炉内的浮力流动或者强旋流动,在很多工况下所给出的结果优于其他模型所得的结果,因为它考虑了浮力效应、近壁效应等,但总体来讲其带来的益处远不及它的计算复杂性,在实际工程预测中并不常见。
燃烧是一种化学反应,受反应器内流动、传热等诸多因素的影响,尤其当其中的流动为湍流时,如何模拟反应与湍流间的相互作用,是一个十分复杂的问题。湍流与反应之间有强烈的相互作用,例如,反应可通过放热引起密度变化而影响湍流;另一方面,湍流可能通过浓度及温度脉动而强化组分的混合与传热,从而显著地反作用于反应速率。一般来说,层流中反应速率取决于分子水平上的混合,而湍流中反应速率则受湍流涡团间混合影响较大。
层流或湍流中瞬时反应率,如果按简单的一步统观反应动力学概念,可表达成如下的Arrhenius公式形式:
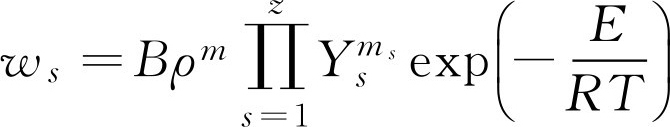
其中, w s 为 S 组分反应率,即单位时间单位体积内产生或消耗的 S 组分物质(kg/m 3 ·s), E 为活化能, R 为通用气体常数, Y s 为 S 组分质量分数, B 为指数前因子, m =∑ m s 为反应级数。为简单起见,设反应为两组分浓度起支配作用的二级反应,其反应率为:
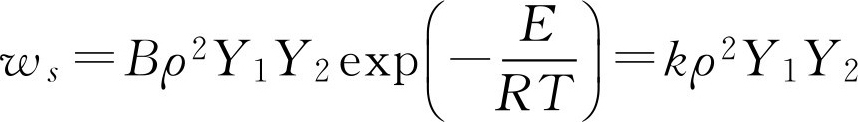
湍流反应模拟的中心问题是反应率的时均值不等于均值的反应率,为了说明这一问题,可对瞬时反应率进行Reynolds展开,即取:
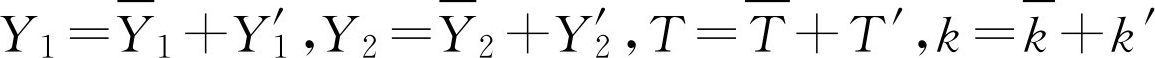
如果忽略密度脉动(即 ρ '=0),则对反应率取时均值后,可有:
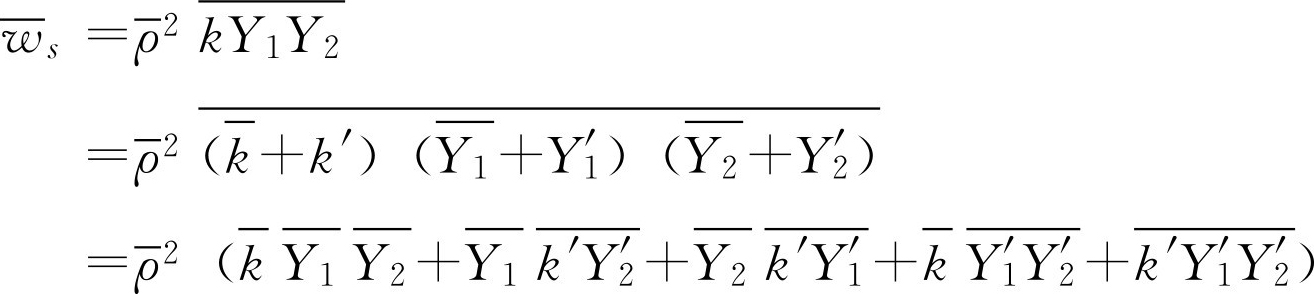
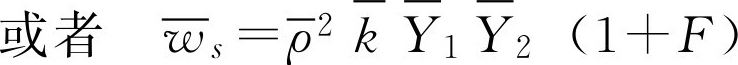
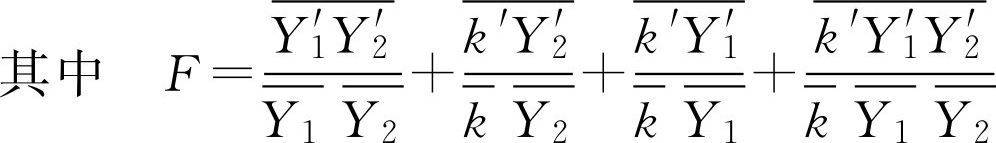
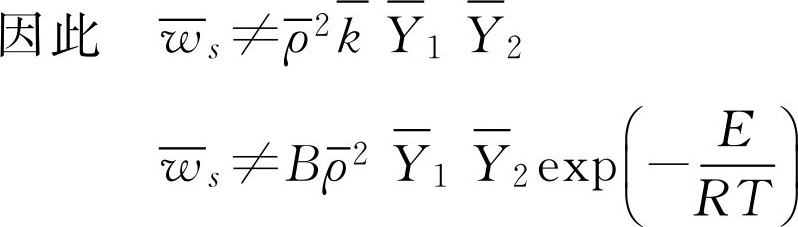
湍流反应模拟的困难在于如何模拟关联项
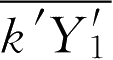 ,
,
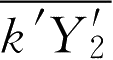 ,
,
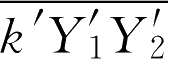 等。由于
k
中含有高度非线性的指数函数,使上述关联项的直接模拟遇到很大困难。有一种办法就是模仿湍流流动模拟,对以上各关联项写出输送方程,然而其封闭问题,特别是源项的处理很麻烦,但可以通过对问题作一定简化后找出可行的封闭方法。
等。由于
k
中含有高度非线性的指数函数,使上述关联项的直接模拟遇到很大困难。有一种办法就是模仿湍流流动模拟,对以上各关联项写出输送方程,然而其封闭问题,特别是源项的处理很麻烦,但可以通过对问题作一定简化后找出可行的封闭方法。
Spalding于20世纪70年代提出了旋涡破碎模型(Eddy-Break-Up Model,简称EBU模型)
[33]
。它是直接由物理上的设想出发,对湍流反应率所作的一种假设,其基本思想是:把湍流燃烧区考虑成未燃气微团和已燃气微团的混合物,化学反应在这两种微团的交界面上发生;化学反应速度取决于燃气微团在湍流作用下破碎成更小微团的速率,破碎速率与湍流脉动动能衰变的速率成正比,如果用
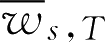 表示涡旋破碎频率,则
表示涡旋破碎频率,则
 ,其中
g
为浓度脉动均方值,
,其中
g
为浓度脉动均方值,
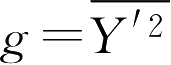 。
。
出于量纲上的考虑,
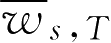 的最终表达式为:
的最终表达式为:
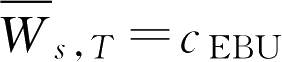 U ρgε/k
U ρgε/k
其中
c
EBU
为经验系数,
c
EBU
=0.35~0.4,对浓度脉动均方值
g
可以简单地假定为
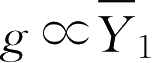 或
或
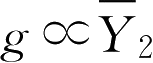 ,或g∝min [
,或g∝min [
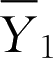 ,
,
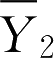 ,
,
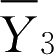 ],在燃烧问题中,
],在燃烧问题中,
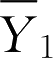 ,
,
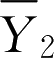 ,
,
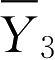 可分别表示燃料、氧化剂、燃烧产物浓度等。其中最后的式子称为Mag-nusen修正的EBU模型。
可分别表示燃料、氧化剂、燃烧产物浓度等。其中最后的式子称为Mag-nusen修正的EBU模型。
EBU模型突出了湍流混合(或者说流动状态)对燃烧速率的控制作用,但它未能考虑分子输送和化学动力学因素的作用,以致在有些化学工程实际问题中产生不可忽视的误差。针对这一不足之处,Magnussen和Hjertager在旋涡破碎模型的基础上作了修正,修正后的模型称之为涡耗散模型(eddy-dissipation model,简称ED模型) [34] 。涡耗散模型弥补了EBU模型的缺陷,获得了广泛的应用。在涡耗散模型中,对于反应 r ,组分 j 的净生成率 R j,r 取为下面前两式求得的最小值,然后以此反应率作为组分守恒方程中的源项。
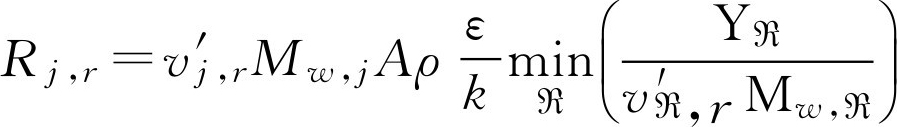
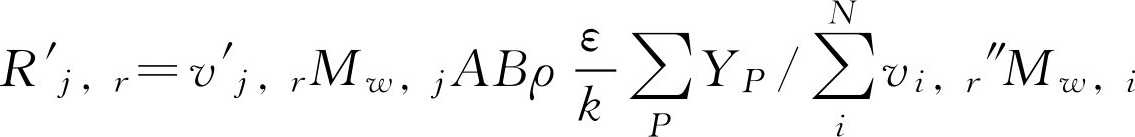
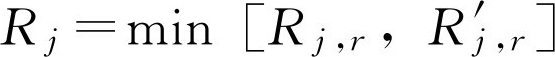
其中,
Y
P
、
Y
R
分别为任一化学产物
P
和特定的反应物
R
的质量组分,
A
,
B
都是经验常数,分别为4.0和0.5,
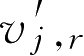 为反应
r
中反应物
j
前的反应系数,
为反应
r
中反应物
j
前的反应系数,
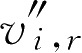 为
r
反应中生成物
i
的反应系数,
N
为化学反应中的物质数,
M
w,j
为物质
j
的分子质量。
为
r
反应中生成物
i
的反应系数,
N
为化学反应中的物质数,
M
w,j
为物质
j
的分子质量。
辐射换热是燃磷塔内传热的主要形式,并直接或间接地影响燃磷塔内其他过程。辐射换热过程有其特殊性,在燃烧装置中,火焰的热辐射与火焰中介质的温度以及介质的辐射吸收、散射能力有关,而介质的辐射、散射能力与辐射波长有关。另外,燃烧空间中任意一点对空间中其他任一点都有辐射换热,燃烧装置的壁面通常对辐射具有反射作用。
由于辐射换热的以上特性,使辐射换热的求解较为复杂、困难。如果给定介质的辐射性质及温度分布(包括壁面温度),火焰及燃烧产物对壁面的辐射换热是可以直接计算出来的。但通常温度是一个未知量,与温度有关的介质辐射性质也有待确定。因此,辐射换热方程与整个能量方程需要耦合求解。辐射换热的贡献体现在能量守恒方程的源项之中。
选择辐射传热模型的主要依据是光学厚度 aL ( a 为吸收系数, L 是所讨论问题的光路长度,在化工工程的燃烧炉中,取为燃烧炉的几何尺寸),因为各个模型适用的光学厚度范围不同。在常用的五种辐射模型中 [35~39] ,DTRM(discrete transfer radiation model)模型适用的光学厚度范围是 aL <1,P- N 模型适用范围是1< aL <3,Rosseland模型适用的范围是 aL >3,DO(discrete ordinates)模型的适用范围是 aL <1,S2 S(surface-to-surface)模型仅适用于没有介质充填的封闭空间,有介质时不一定总是有效。相较于其他模型,P- N 模型不仅考虑了发射和散射的影响,还考虑了气体和其中液、固粒子的相互热交换。
P- N 模型,即球形谐波法( N 表示级数的阶数)是Jeans研究星际辐射时提出的,后来经Murray、Davison和Lourganoff进一步完善并应用于求解一维辐射传热问题。球形谐波法的求解思想为:将当地辐射强度用具有正交性质的球谐函数展开,并将级数和截成 N 项,同时对散射相函数按多项式展开,代入微分形式的辐射传递方程,求解辐射换热问题。
理论上,随着阶数 N 的增大,解的精度不断缓慢提高,当 N 为无穷时,趋近于精确解。但是,随着阶数的增加,数学上的复杂性与计算量也急剧增加。目前较为实用且广泛采用的是P-1模型,即一阶球形谐波法。P-1辐射模型是P- N 模型中最简单的一种,它将辐射强度 I 展开成正交的球谐函数的级数。
两步法热法磷酸生产工艺包括燃烧与水化两个步骤,其中燃烧过程在燃磷塔内进行,液态磷和一次空气通过磷喷枪的同轴圆环套进入喷枪,液态磷经一次空气剪切为雾滴,并在二次空气的共同作用下开始燃烧,燃烧产生的热量使液态磷汽化而使燃烧过程持续进行,这是一个复杂的两相流燃烧过程。由于两相流在塔内复杂的运动及其燃烧的相互作用,其最高燃烧的局部温度高达2600~2800℃,很难用实验方法对内部各点的流场、温度场和浓度场等物理参数进行测试。因此为获取燃磷塔运行过程中塔内的局部细节信息,进一步实现燃磷塔的优化设计,采用CFD数值模拟方法很有必要。然而燃磷塔内部涉及流动、传热和反应等多个过程,开展符合实际的数值模拟具有一定难度,迄今将CFD技术与热法磷酸生产相结合的文献报道很少。目前仅郭印诚、刘宝庆等公开发表了有关燃磷塔数值模拟的文章。其中郭印诚等首次在全面考虑燃磷塔内磷的燃烧、湍流流动及辐射传热等物理机制的基础上,建立了基于标准 k-ε 模型、P-1辐射模型等的数值模拟方法,并针对云南省磷化工中试基地所提供的燃磷塔设计结构,进行了磷燃烧过程的数值模拟,其模拟获得的壁面热流值与现场试验结果符合较好 [40] 。此后,刘宝庆等针对240kg/h燃磷塔的流场、温度场和组分浓度场也进行了模拟,并进行了相关影响因素的分析,为燃磷塔的优化运行提供了指导 [41] 。但上述研究都对燃磷塔结构、物性进行了较大的简化,且针对的都是小型燃磷塔,同时相关研究未考虑结构因素如高径比、塔型等的影响,故有必要开展更加深入的数值计算,以指导实际工程设计。