





模糊数学是研究和处理模糊性现象的一种数学理论和方法。模糊集是模糊数学的理论基础。此处所谓的模糊性,主要是指客观事物的差异在中间过渡过程中的不分明性,如某一生态条件对某种害虫、某种作物的存活或适应性可以评价为“有利、比较有利、不那么有利、不利”等状态;人从身高的角度可以分为“很高、高、中等、矮、很矮”等。这些通常是本来就属于模糊的概念,为借助计算机模拟人类处理分析这些“模糊”概念的数据,便产生了模糊集合论。
 2.1.1 模糊集的定义
2.1.1 模糊集的定义
模糊数学将经典数学的应用范围从清晰、精确的传统领域拓展到了模糊领域,相应的将经典集合理论也扩展为模糊集合理论。
定义2.1 已知论域 U ,在其上做映射 A ,有
A : U →[0,1], u ∈ U
u → A ( u ), A ( u )∈[0,1]
则称映射 A 是 U 上的一个模糊集,记作 A , A ( u )称为 F 集 A 的隶属函数(或称 u 对 A 的隶属度)。
约定:
为方便,本书将模糊简记为
F
,论域
U
上的模糊集记为
F
集。论域
U
上的
F
集合的全体用
F
(
U
)来表示,本书中称其为模糊幂集,易知空集
 与论域
U
都属于
F
(
U
)。
与论域
U
都属于
F
(
U
)。
由上述定义不难看出,普通经典集合与 F 集合的差别主要就在于特征函数的值域取值范围,前者是离散集合 {0,1},后者是连续闭区间[0,1]。因此可以认为 F 集是普通集的推广,而普通集是 F 集的一种特殊情况。
通常情况下,根据论域 U 中元素的个数不同分为有限论域与无限论域。有限论域 U 上的一个 F 集合 A 有如下几种表示方法:
(1)Zadeh表示法
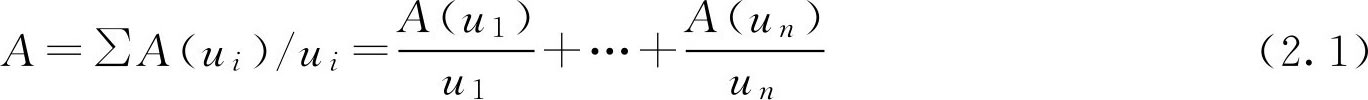
(2)向量表示法
A =( A ( u 1 ), A ( u 2 ),…, A ( u n )) (2.2)
(3)序偶表示法
A ={( u , A ( u )) u ∈ U ,0≤ A ( u )≤1} (2.3)
如果 U 是无限论域, F 集合 A 可表示为
A =∫ A ( u )/ u (2.4)
注意: 式中“/”不是通常的分数线,只是一种记号,它表示论域 U 上的元素 u 与隶属度 A ( u )之间的对应关系;符号“∑”及“∫ ” 也不是通常意义下的求和与积分符号,都只是表示 U 上的元素 u 与其隶属度 A ( u )的对应关系的一种体现。
例2.1 设某学习小组共5人,用论域 U ={1,2,3,4,5}表示,现在对每个同学的性格稳重程度打分,按百分制打分再都除以100,则给定一个 U 到区间[0,1]间的映射,按照 F 集的定义可把“性格稳重程度”看作一个 F 集合 A ∈ F ( U ),各值属于 A 的程度与其隶属度 A ( u i )如表2.1所示:
表2.1 性格稳重程度

请用 F 集的表示方式表示 F 集合 A 。
解:
A 可用不同的方式表示为
(1)
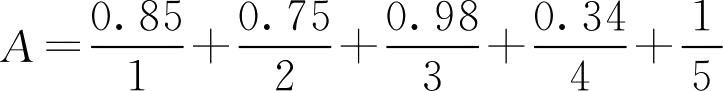
(2) A ={(0.85,1),(0.75,2),(0.98,3),(0.34,4),(1,5)}
(3) A =(0.85,0.75,0.98,0.34,1)
例2.2 在标志年龄[0,150]的实数轴上,标记出“老年人”和“青年人”的区间。故取论域 U =[0,150], F 集合 A 与 B 分别表示“老年人”和“青年人”。给出他们的隶属函数(图2.1)分别为
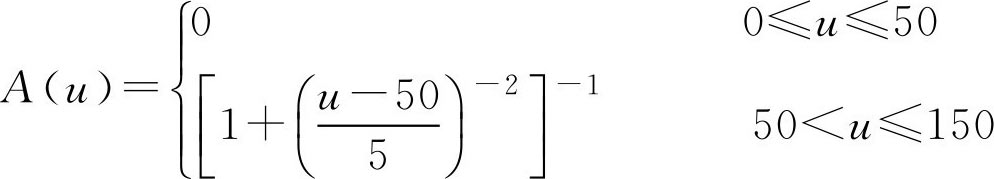
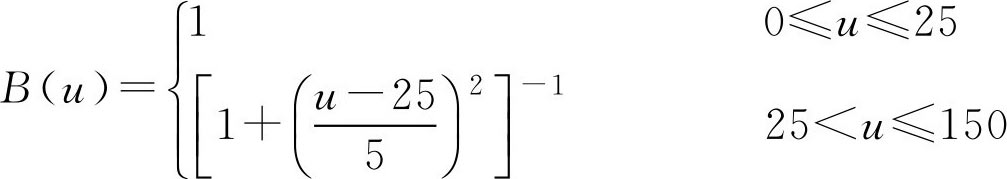
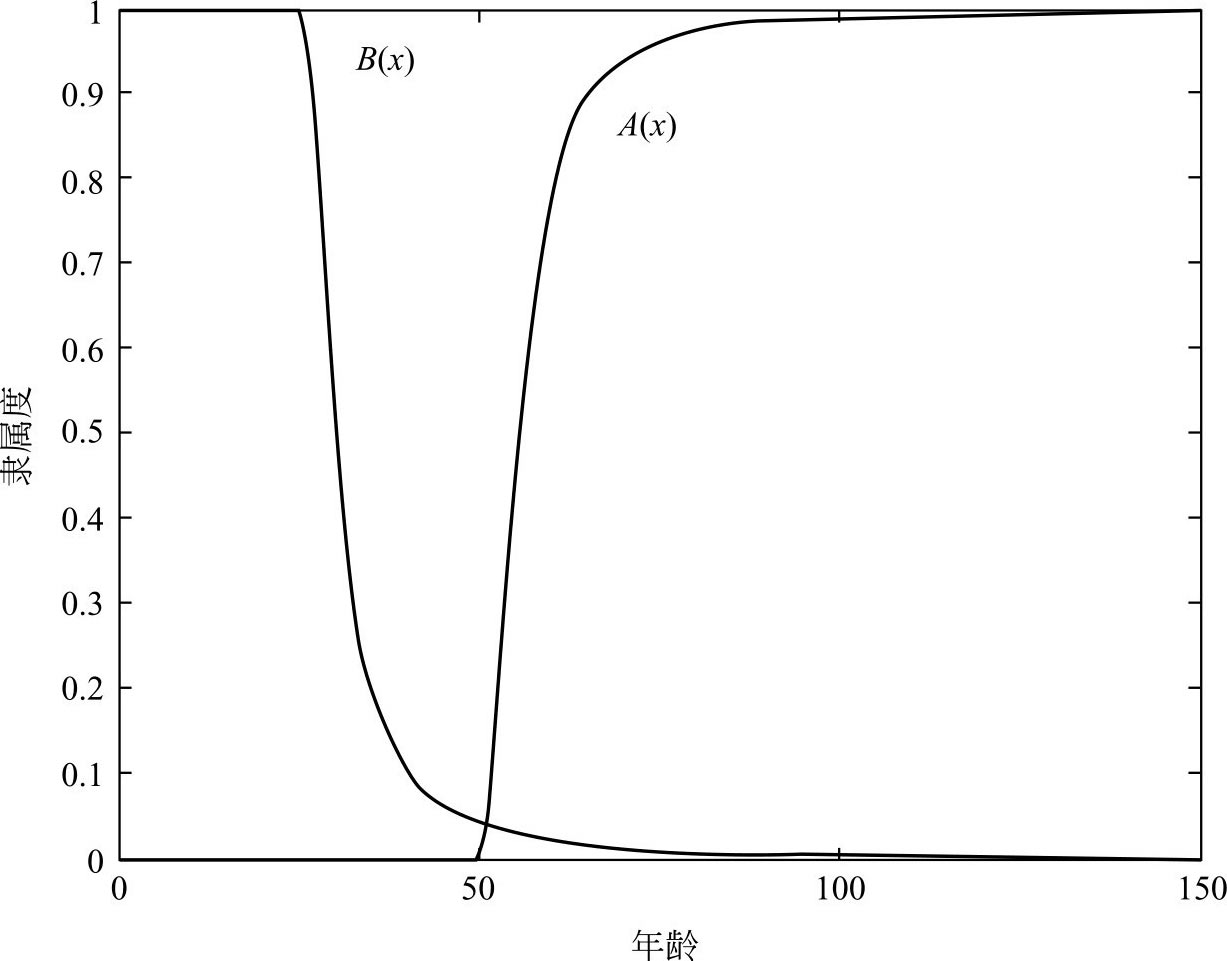
图2.1 老年人与青年人隶属函数
请用 F 集的表示方式表示 F 集合 A 与 B 。
解:
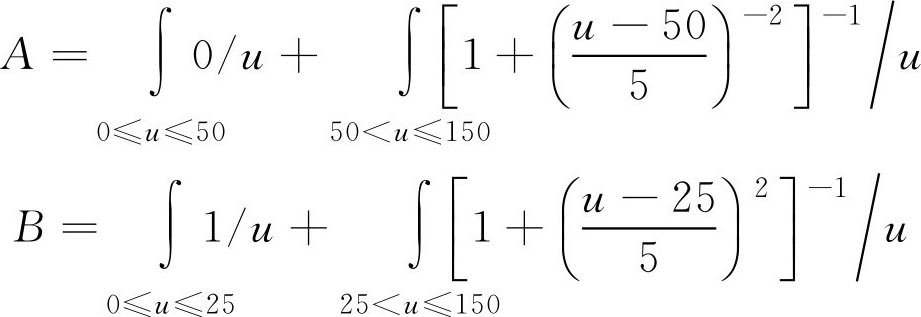
说明: 当 u 取50岁以下各年龄值时, A ( u )=0,表示50岁以下不属于“老年人”这一集合;当 u 取值超过50岁,并逐渐增大时,对于“老年人”这一集合的隶属度也愈来愈大,如果 u =70,有 A (70)=0.94,表明年龄为70岁时属于“老年人”的隶属度已达94%。相应的,对于 F 集 B 的隶属函数 B ( u )也可类似地分析各取值的含义。
 2.1.2 模糊集的运算
2.1.2 模糊集的运算
两个
F
集间的各种运算,实际上就是逐点对两个
F
集相应的隶属函数作运算。本书为了描述方便,采用符号“
 ”表示“对任意”。
”表示“对任意”。
设
A
,
B
∈
F
(
U
),若
 u
∈
U
,
B
(
u
)≤
A
(
u
),则称
A
包含
B
,或者称
B
包含于
A
,记为
B
u
∈
U
,
B
(
u
)≤
A
(
u
),则称
A
包含
B
,或者称
B
包含于
A
,记为
B
 A
;如果
A
A
;如果
A
 B
且
B
B
且
B
 A
,则称
A
与
B
相等,记作
A
=
B
。
A
,则称
A
与
B
相等,记作
A
=
B
。
定义2.2 设 A , B ∈ F ( U ),分别称运算 A ∪ B , A ∩ B 为 A 与 B 的并集、交集。称 A c 为 A 的补集,也称为余集。他们的隶属函数分别为
( A ∪ B )( u )=max( A ( u ), B ( u )) (2.5)
( A ∩ B )( u )=min( A ( u ), B ( u )) (2.6)
A c ( u )=1- A ( u ) (2.7)
约定: 为方便,本书将两个 F 集的取大运算记做max[ A ( u ), B ( u )]= A ( u )∨ B ( u ),两个 F 集的取小运算记做min( A ( u ), B ( u ))= A ( u )∧ B ( u )。
因为
 a
,
b
∈[0,1],都有0≤
a
∨
b
≤1,0≤
a
∧
b
≤1,0≤1-
a
≤1,故对任意
A
,
B
∈
F
(
U
),有
A
∪
B
,
A
∩
B
,
A
c
∈
F
(
U
)。
a
,
b
∈[0,1],都有0≤
a
∨
b
≤1,0≤
a
∧
b
≤1,0≤1-
a
≤1,故对任意
A
,
B
∈
F
(
U
),有
A
∪
B
,
A
∩
B
,
A
c
∈
F
(
U
)。
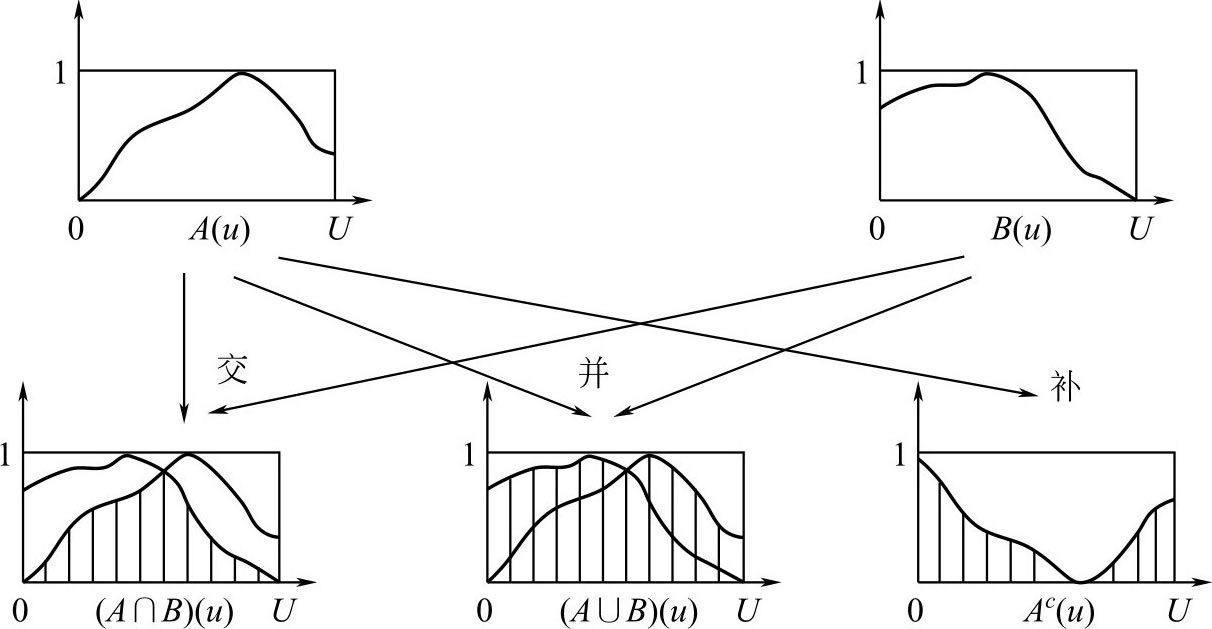
图2.2 F 集的交、并、补运算结果
一般地, F 集 A 与 B 的并、交和余的计算(图2.2),按照论域 U 的有限和无限的不同,可以分为以下两种情况表示:
①设论域
U
={
u
1
,
u
2
,…,
u
n
},
F
集
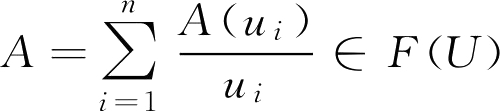 ,
F
集
,
F
集
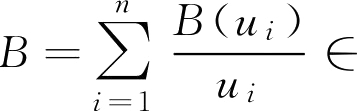
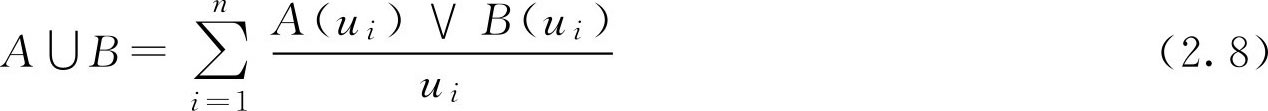
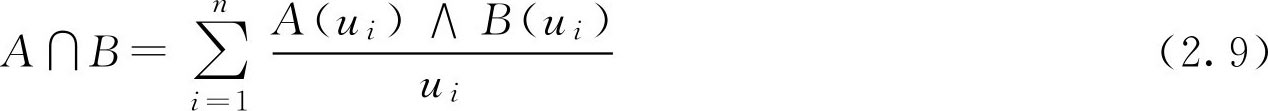

②设论域
U
为无限集,
F
集
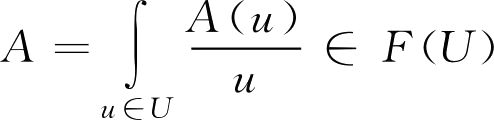 ,
F
集
,
F
集
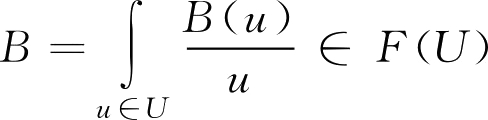 ,则有
,则有
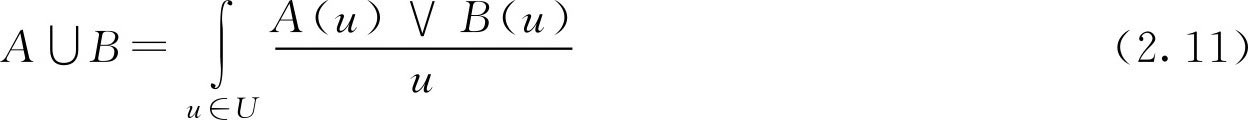
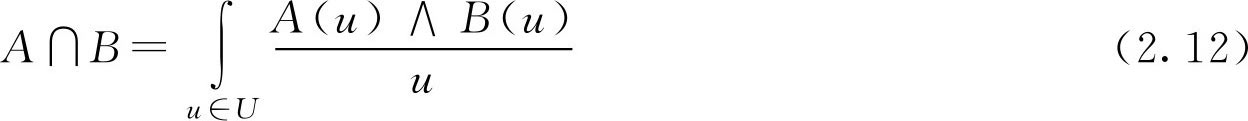

两个 F 集间的并、交运算可以推广到任意多个 F 集间的并、交运算。
推广: 设 A t ∈ F ( U ), t ∈ T , T 为指标集。对任意 u ∈ U ,有
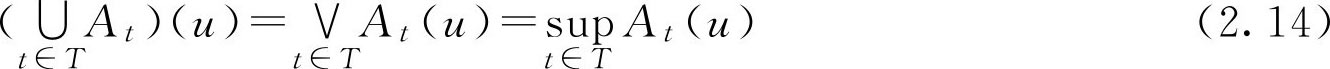
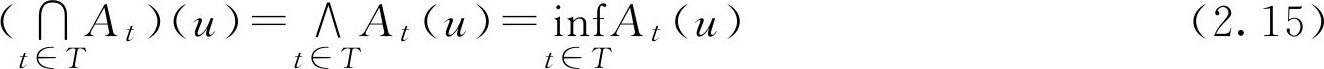
其中sup和inf分别表示全体F集“取最大”和“取最小”运算。显然,
 。
。
设 U 表示论域, A , B , C ∈ F ( U ),有如下性质:
(1)幂等律 A ∪ A = A , A ∩ A = A
(2)交换律 A ∪ B = B ∪ A , A ∩ B = B ∩ A
(3)结合律( A ∪ B )∪ C = A ∪( B ∪ C ),( A ∩ B )∩ C = A ∩( B ∩ C )
(4)吸收律( A ∪ B )∩ A = A ,( A ∩ B )∪ A = A
(5)分配律( A ∪ B )∩ C =( A ∩ C )∪( B ∩ C ),( A ∩ B )∪ C =( A ∪ C )∩( B ∪ C )
(6)0—1律 A ∪∅= A , A ∩∅=∅, A ∪ U = U , A ∩ U = A
(7)复原律 ( A c ) c = A
(8)对偶律( A ∪ B ) c = A c ∩ B c ,( A ∩ B ) c = A c ∪ B c
证明:
此处仅证明对偶率( A ∪ B ) c = A c ∩ B c ,其余由读者自行完成。
 u
∈
U
,(
A
∪
B
)
c
(
u
)=1-(
A
∪
B
)(
u
)
u
∈
U
,(
A
∪
B
)
c
(
u
)=1-(
A
∪
B
)(
u
)
=1- A ( u )∨ B ( u )
=(1- A ( u ))∧(1- B ( u ))
= A c ( u )∧ B c ( u )
=( A c ∩ B c )( u )
故( A ∪ B ) c = A c ∩ B c 。
例2.3 设论域 U ={ u 1 , u 2 , u 3 , u 4 , u 5 }, A =(0.2,0.5,0.8,0.7,0.2), B =(0.8,0.2, 1,0.4,0.3),计算 A ∪ B , A ∩ B , A c 。
解:
A ∪ B =(0.2∨0.8,0.5∨0.2,0.8∨1,0.7∨0.4,0.2∨0.3)
=(0.8,0.5,1,0.7,0.3)
A ∩ B =(0.2∧0.8,0.5∧0.2,0.8∧1,0.7∧0.4,0.2∧0.3)
=(0.2,0.2,0.8,0.4,0.2)
A c =(1-0.2,1-0.5,1-0.8,1-0.7,1-0.2)=(0.8,0.5,0.2,0.3,0.8)
例2.4 求例2.2中两个 F 集的交、并等运算,包括 A ∪ B , A ∩ B , A c 。
解:
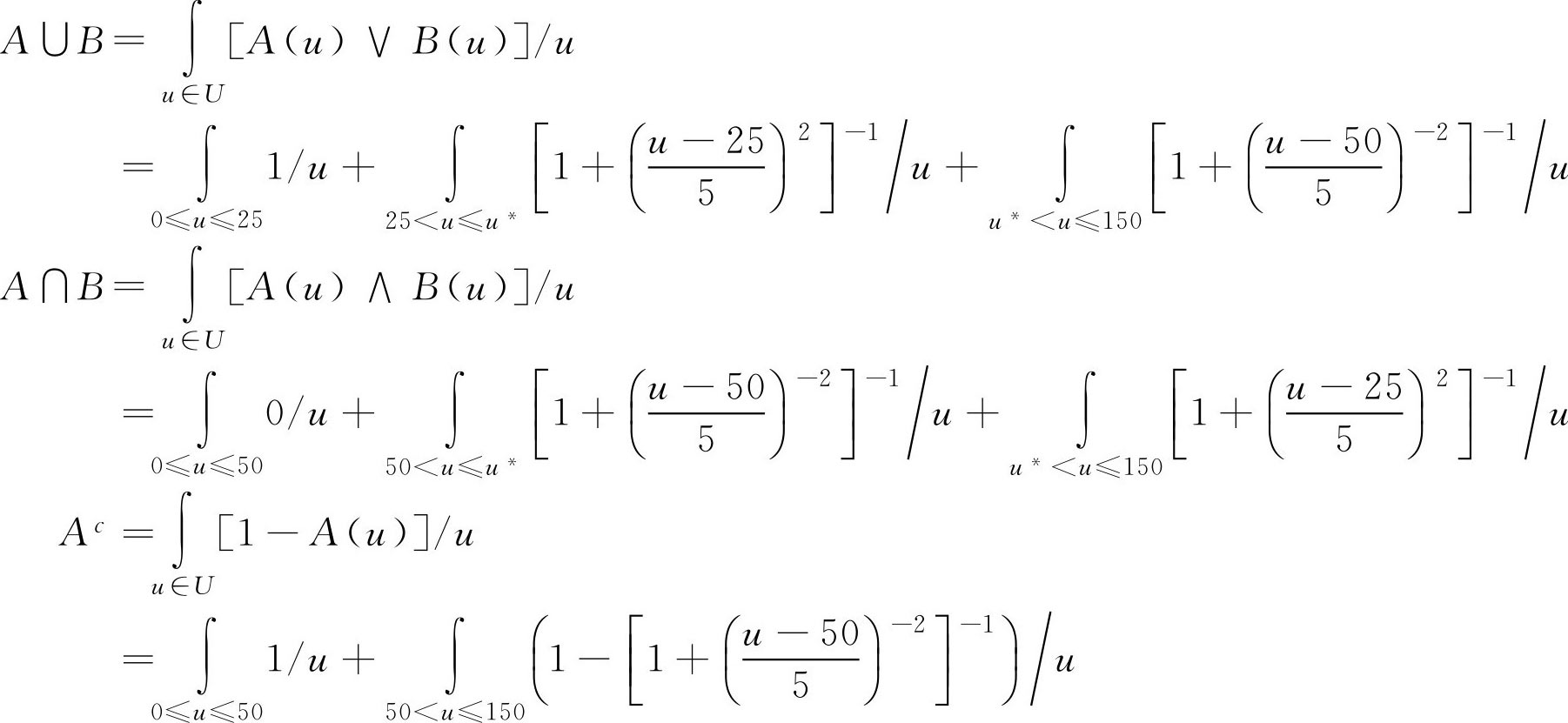
注意: 例2.4中的 u * 表示两个隶属函数的交点。
 2.1.3 隶属函数的确定方法
2.1.3 隶属函数的确定方法
从定义2.1可知,隶属函数是对 F 概念的定量描述。我们遇到的 F 概念不胜枚举,然而准确地反映 F 概念的 F 集合的隶属函数,却无法找到统一的模式。如何正确地确定隶属函数,是运用 F 集合理论解决实际问题的基础,本部分给出研究描述模糊现象和确定隶属函数的一般方法。
在很多情况下,隶属函数可以通过 F 统计试验的方法来确定,此处利用确定 F 集“青年人”的隶属函数为例子来说明。
以人的年龄作为论域 U ,调查 n 个人选,请他们认真考虑“青年人”的含义后,提出自己认为的“青年人”最合适的年龄区间,如表2.2所示(统计129人后给出的结果)。
表2.2 关于青年人年龄区间的调查结果
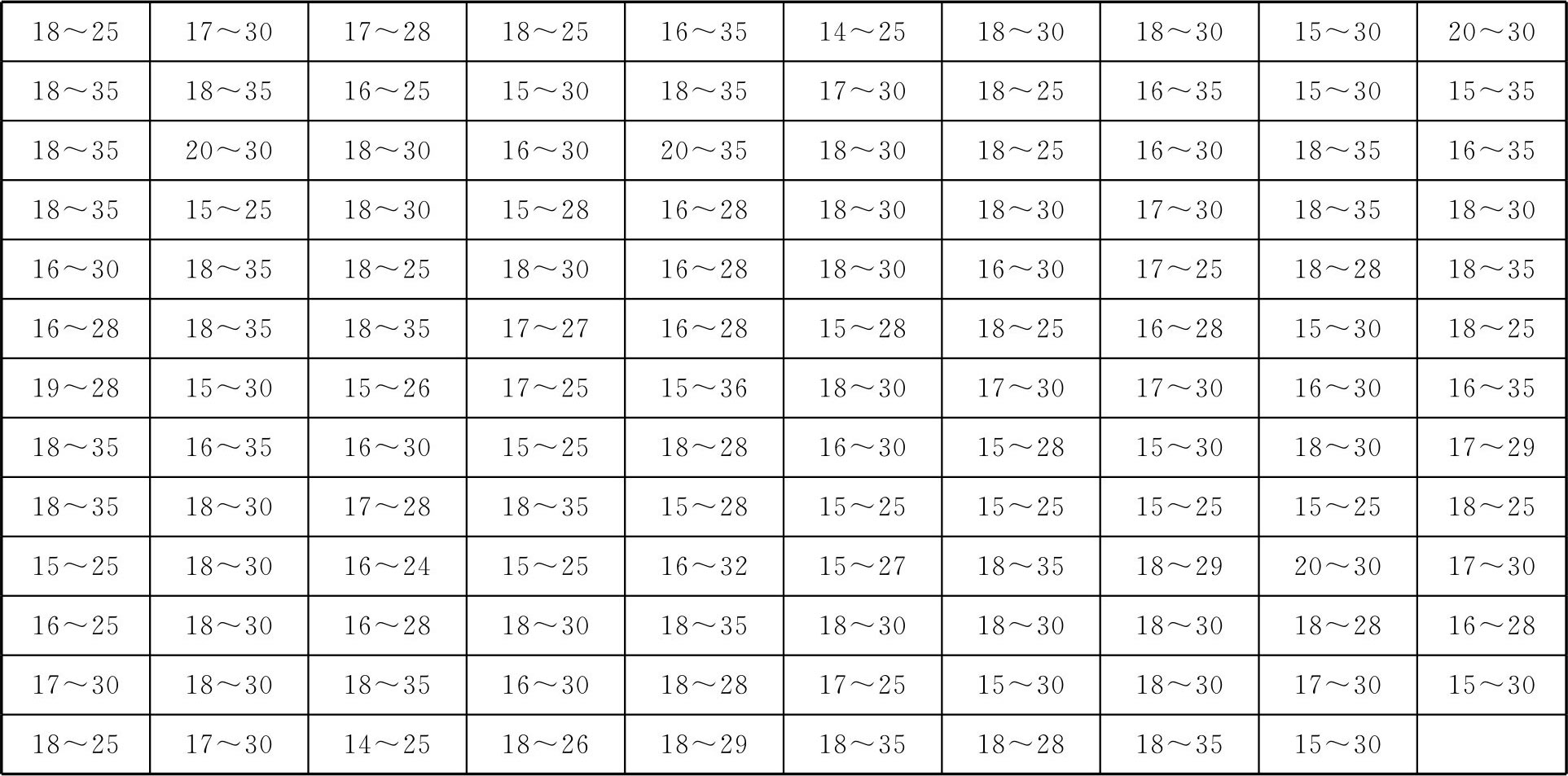
为了确定某个年龄(如 u 0 =27)隶属于“青年人”这一 F 集合 A 的程度,尝试进行如下试验,计算出27岁被 n 个人给出的年龄区间的覆盖次数 m ,则称 m / n 为27岁对于“青年人”的隶属频率。表2.3给出了部分抽样调查结果。
表2.3 27岁对青年人的隶属频率

容易发现,随着 n 的个数增加,27岁隶属于“青年人”这一集合的频率逐步稳定在0.78附近,因而可取
A (27)=0.78
接着,考虑“青年人”的隶属函数。将论域 U 进行分组处理,每组以中值为代表分别计算各组的隶属频率,即可确定出14~37岁各年龄隶属于 F 集 A 的隶属度,其隶属度函数曲线如图2.3所示。
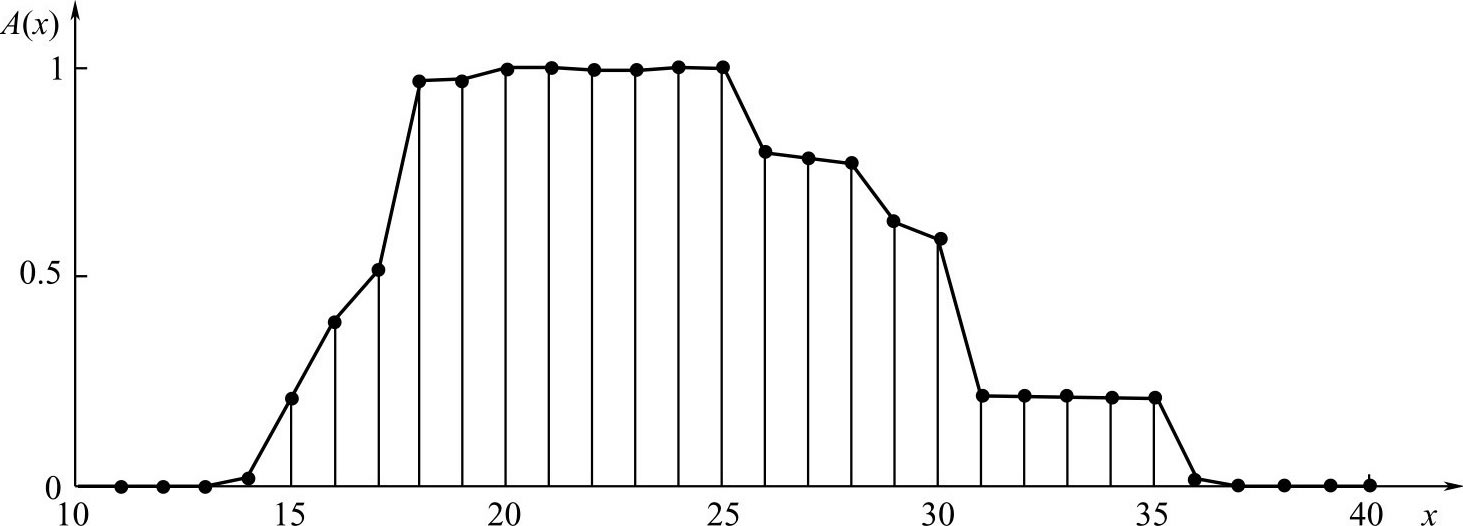
图2.3 青年人的隶属函数
注意: 从图2.3获得具体隶属函数表达式的方法可以利用数值分析中的插值或拟合的方法,亦可利用下面将要讲述的 F 分布法。
统计试验方法可以比较客观地反映论域中元素相对于 F 概念的隶属程度,也具有一定的理论基础,因而是一种常用的确定隶属函数的方法。但需要指出的是, F 统计与概率统计是有本质区别的:一般说来,概率统计可以理解为“变动的点”是否落在“不动的圈内”,而 F 统计则可理解为“变动的圈”是否能够覆盖住“不动的点”。
人们对于客观事物的描述分析,主要可以分为偏大型、中间型和偏小型,比如描述人的体型可以说“胖”、“适中”和“瘦”,描述温度可以说“冷”、“适中”和“热”,而这些都是以实数 R 作为论域的情形。通常,人们把实数集 R 上 F 集的隶属函数称为 F 分布。当所讨论的客观模糊现象的隶属函数与某种已知的 F 分布相类似时,即可选择这个 F 分布作为所求的隶属函数,然后再通过先验知识或数据实验确定符合实际的 F 分布中的各未知参数,从而得到具体的 F 集的隶属函数。
本书给出几种常见的 F 分布及其图形,以供读者参考选择。
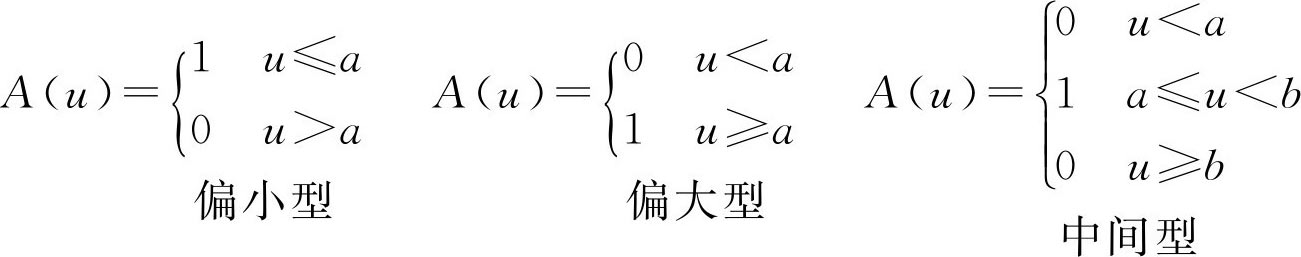


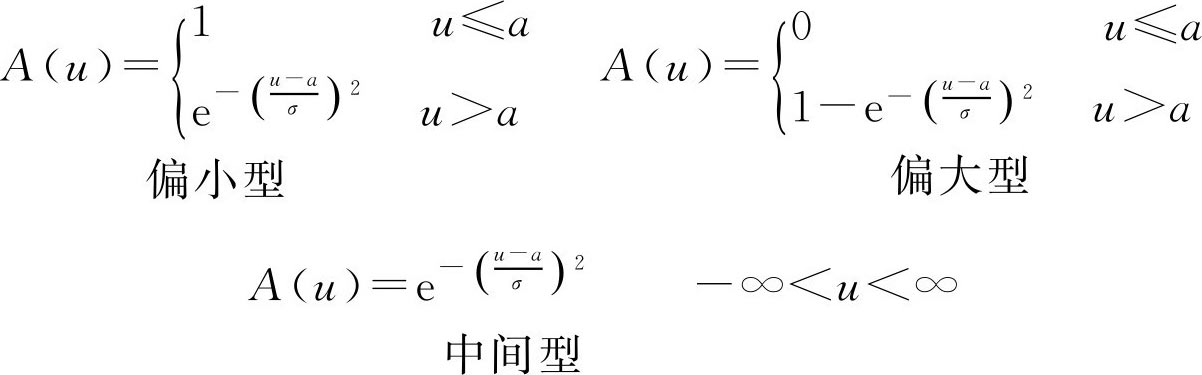



本书给出了六种 F 分布,在实际应用中请根据讨论对象所具有的特点加以选择。或者可以根据统计资料描述出大致曲线,结合 F 统计方法选择最接近的一个,再根据实际情况确定出较符合实际的参数即可。
注意: 数学软件MATLAB包含模糊数学工具箱,其中提供了丰富的 F 分布函数,可供读者直接利用。
三分法是用随机分界点的思想来处理模糊性的统计试验模型。下面通过建立“矮个子”、“中等个子”、“高个子”三个 F 集的隶属函数来给出三分法的具体步骤。
设论域 U =(0,3),单位为米, A 1 , A 2 , A 3 ∈ F ( U )为相应的三个 F 集,因为每次模糊试验可以确定 U 的一个划分,而每次划分恰好可以确定一对数( ξ , η ),其中 ξ 表示矮个子与中等个子的分界点, η 表示中等个子与高个子的分界点。反之,如果能够给出数对( ξ , η ),则把论域 U 划分为矮个子、中等个子和高个子三个部分。即( ξ , η )确定了映射 e ,有
e ( ξ , η ): U →{ A 1 , A 2 , A 3 }
因为矮个子、中等个子和高个子的区间是随机区间,则 ξ 和 η 是具有正态分布的随机变量,即
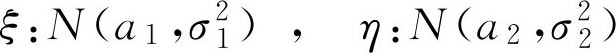
从而有
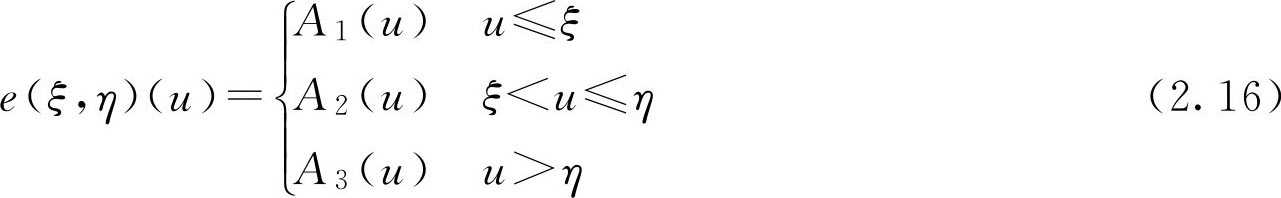
概率 P { u ≤ ξ }是随机变量 ξ 落在区间[ u , b )的可能性的大小。若 u 增大,则区间[ u , b )变小,落在区间[ u , b )的可能性也随之变小。概率 P { u ≤ ξ }的这一特性与矮个子 F 集 A 1 相同,从而有
类似的,有
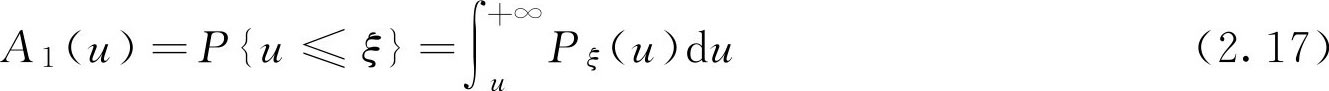
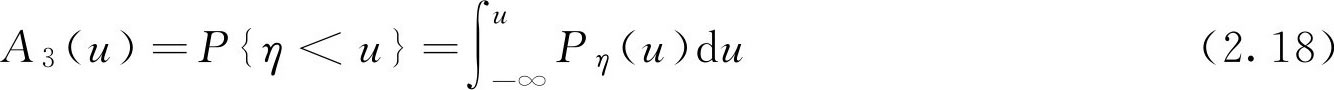
这里的
P
ξ
(
u
),
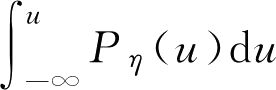 表示随机变量
ξ
和
η
的概率密度,而
表示随机变量
ξ
和
η
的概率密度,而
A 2 ( u )=1- A 1 ( u )- A 3 ( u ) (2.19)
这其中
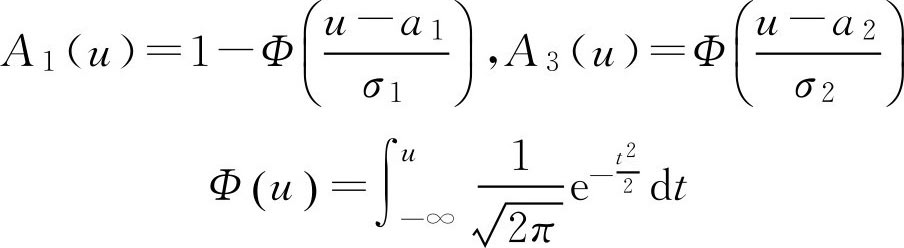
 2.1.4 模糊集的截集
2.1.4 模糊集的截集
虽然模糊集合能够客观地反映现实中存在的模糊概念,但在处理实际问题的过程中,特别是要最后作出判断或决策时,往往又需要将模糊集合化成各种不同的普通集合,这就需要在模糊集合与普通集合间架起一座桥梁,使得模糊集和普通集能够相互转化,这种任务通常由 λ 水平截集来完成。
定义2.3 设 A ∈ F ( U ), λ ∈[0,1],记
A
λ
={
u
|
 u
∈
U
,
A
(
u
)≥
λ
} (2.20)
u
∈
U
,
A
(
u
)≥
λ
} (2.20)
称 A λ 为 F 集 A 的 λ 截集, λ 称为阈值(或置信水平)。
例2.5
设
A
∈
F
(
R
),
R
为实数域,其隶属函数为
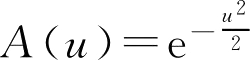 ,求
A
0.5
。
,求
A
0.5
。
解:
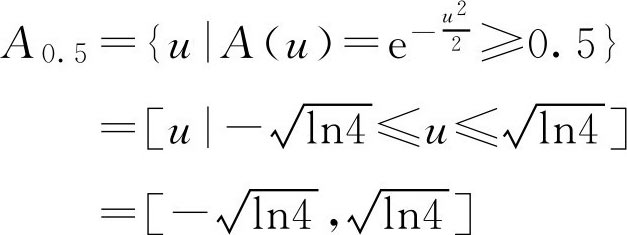
说明: F 集 A 的 λ 截集 A λ 是一个普通集合,它是通过对 A 在 λ 水平上的截取实现的。
例2.6 在古代史分期中,记奴隶社会为 F 集 A ,其表示如下
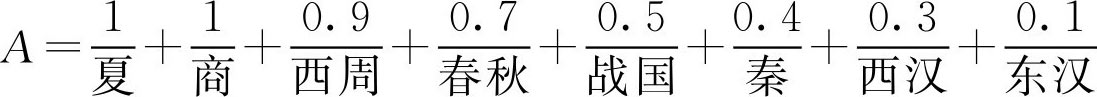
若取 λ =0.5的截集作为奴隶社会的划分界限,问奴隶社会包含哪些朝代?
解:
A 0.5 ={夏,商,西周,春秋,战国}
定义2.4 设 A ∈ F ( U ),记
Supp A ={ uu ∈ U , A ( u )>0},K er A ={ uu ∈ U , A ( u )=1} (2.21)
分别称Supp A 、Ker A 为 F 集 A 的支集与 A 的核。
由定义可知,核是由 F 集 A 中隶属度等于1的元素组成的普通集合,核中的元素是完全隶属于集合 A 的,而支集则是由 A 中隶属度大于0的元素组成的普通集合,如果引入变动的水平 λ ,让其从1趋于0,则 A λ 将从核开始不断扩大,把越来越多的元素吸收进来,最终变成 A 的支集。因此,普通的截集集合族{ A λ } λ∈ [0,1] 就像一个具有游移边界的集合,一个可变的、运动的集合,一个具有包含关系的集合套。
在例2.6中, F 集 A 的核与支集分别为
Ker A ={夏,商}
Supp A ={夏,商,西周,春秋,战国,秦,西汉,东汉}
定义2.5 设 A ∈ F ( U ), λ ∈[0,1],定义 λA ∈ F ( U ),它的隶属函数为
( λA )( u )= λ ∧ A ( u ) (2.22)
F 集 λA 称为数 λ 与 F 集 A 的乘积。
特别的,若 A 是普通集合,则有
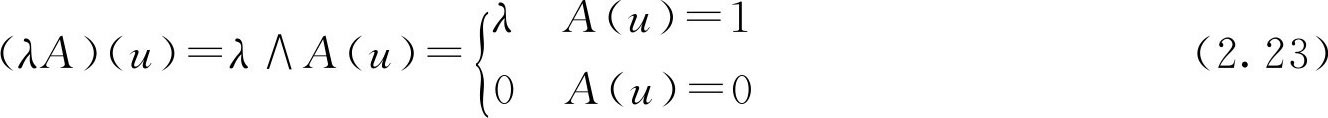
此处的 λA 也为 F 集。
不难证明, λ 与 F 集 A 的乘积 λA 具有如下性质:
性质1
若
λ
1
≤
λ
2
,则
λ
1
A
 λ
2
A
;
λ
2
A
;
性质2
若
A
 B
,则
λA
B
,则
λA
 λB
。
λB
。
证明略。
λ 截集有如下性质( λ ∈[0,1])。
性质1 设 A , B ∈ F ( U ),则
( A ∪ B ) λ = A λ ∪ B λ ,( A ∩ B ) λ = A λ ∩ B λ (2.24)
证明:
( A ∪ B ) λ ={ u |( A ∪ B )( u )≥ λ }={ u|A ( u )∨ B ( u )≥ λ }
={ u|A ( u )≥ λ }∪{ u|B ( u )≥ λ }= A λ ∪ B λ
而( A ∩ B ) λ ={ u ( A ∩ B )( u )≥ λ }={ uA ( u )∧ B ( u )≥ λ }
={ u|A ( u )≥ λ }∩{ u|B ( u )≥ λ }= A λ ∩ B λ 。
对于 F ( U )中的有限个 F 集,性质1仍然成立,即上式中 T 表示有限指标集。
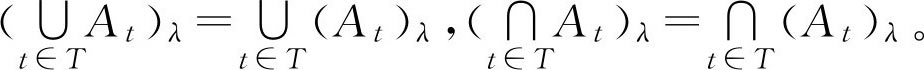
但是,对于无限个 F 集的并,性质1中的等号未必成立,一般有如下结论。
性质2
若{
A
t
t
∈
T
}
 F
(
U
),则
F
(
U
),则
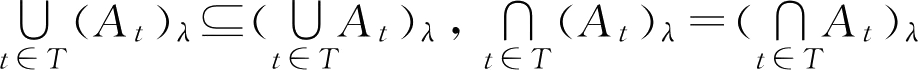
证明:
(仅证第一式)
设
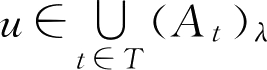 ,则存在
t
0
∈
T
,使得
,则存在
t
0
∈
T
,使得
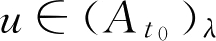 ,于是
,于是
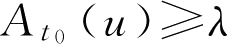 ,即
,即
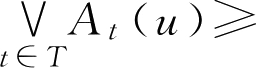
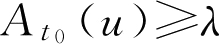 ,故
,故
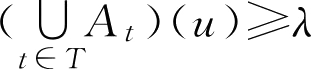 ,从而有
,从而有
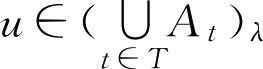 。
。
第二式的证明由读者自行完成。
例2.7
设有无限论域
U
,其上的
F
集
A
n
(
n
=1,2,…)的隶属函数为
A
n
(
u
)=
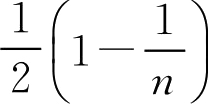 ,请分别求解
,请分别求解
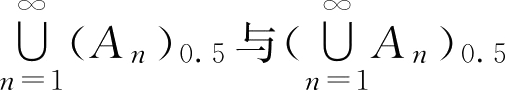 。
。
解:
 u
∈
U
,则有
u
∈
U
,则有
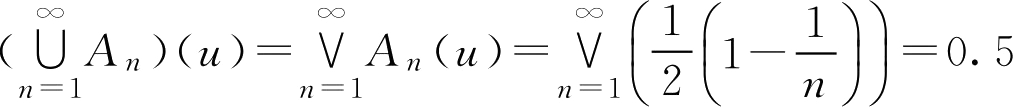 ,即
,即
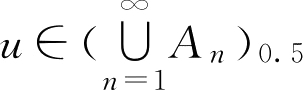 ,于是
,于是
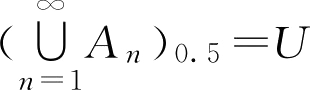 。
。
但是,对于
 u
∈
U
,有
u
∈
U
,有
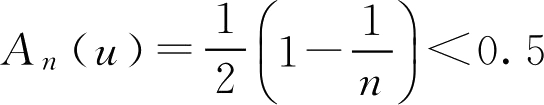 ,则有(
A
n
)
0.5
=
,则有(
A
n
)
0.5
=
 ,
n
≥1,从而有
,
n
≥1,从而有
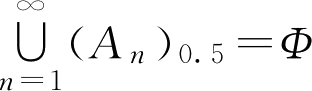 。
。
可见,性质2中的包含关系不能写成等式。
性质3
设
λ
1
,
λ
2
∈[0,1],
A
∈
F
(
U
)。若
λ
2
>
λ
1
,则
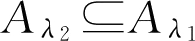 。
。
证明:
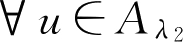 ,有
A
(
u
)≥
λ
2
>
λ
1
,即
,有
A
(
u
)≥
λ
2
>
λ
1
,即
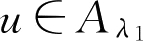 ,则
,则
 。
。
从性质3可知,截集水平越低, A λ 所包含的元素个数越多, A λ 越大;反之,截集水平越高, A λ 越小。特别的,当 λ =1时, A λ 最小,当 λ =0时, A λ 最大。
性质4
设
 t
∈
T
,
λ
t
∈[0,1]则
t
∈
T
,
λ
t
∈[0,1]则
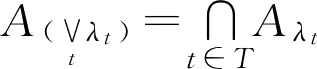 。
。
证明:
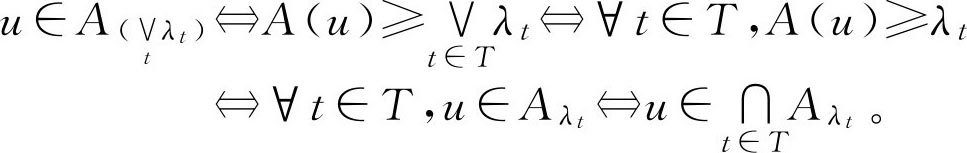
 2.1.5 模糊集的分解定理
2.1.5 模糊集的分解定理
分解定理是模糊数学理论发展的重要组成部分,它给出了如何把 F 集分解成普通集,从而可把 F 集里的问题化成普通集里的问题来讨论,前文介绍的 λ 截集概念,实际上给出了一种把 F 集化为普通集的方法。
定理2.1(分解定理) 设 A ∈ F ( U ),则

证明:
 u
∈
U
,则有
u
∈
U
,则有
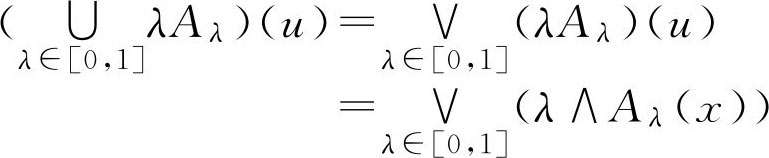
由于 λ 与 A λ ( u )之间的大小不确定,为此给出如下讨论:
当 λ ≤ A ( u )⇒ u ∈ A λ ⇒ A λ ( u )=1⇒ λ ∧ A λ ( x )= λ
当 λ > A ( u )⇒ u ∉ A λ ⇒ A λ ( u )=0⇒ λ ∧ A λ ( x )=0
所以
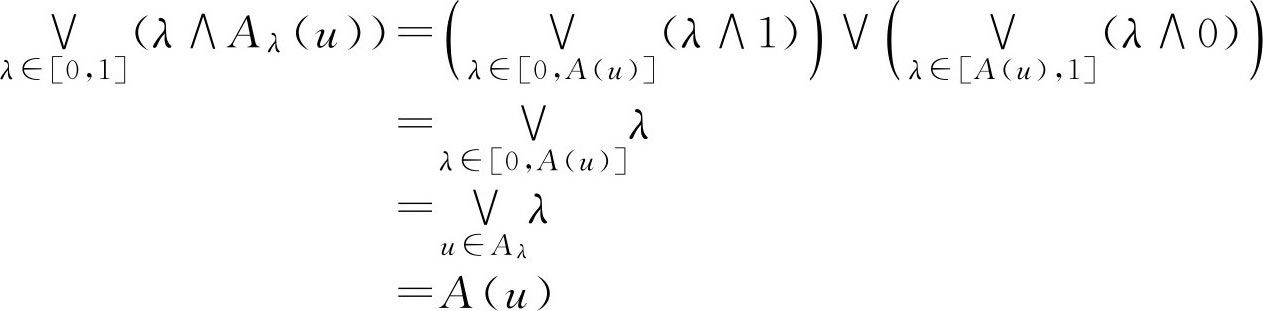
即
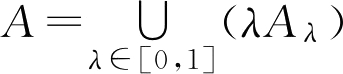
F
集
λA
λ
的隶属函数
分解定理反映了 F 集与普通集的相互转化关系。
例2.8
设
F
集
 ,取
λ
截集,得到
,取
λ
截集,得到
A 1 ={ u 3 }
A 0.9 ={ u 1 , u 3 }
A 0.7 ={ u 1 , u 3 , u 4 }
A 0.3 ={ u 1 , u 3 , u 4 , u 5 }
A 0.1 ={ u 1 , u 2 , u 3 , u 4 , u 5 }
将
λ
截集写成
F
集的形式,例如
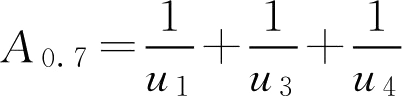 。于是按数与
F
集的乘积定义,得
。于是按数与
F
集的乘积定义,得

应用分解定理即可构成原来的 F 集
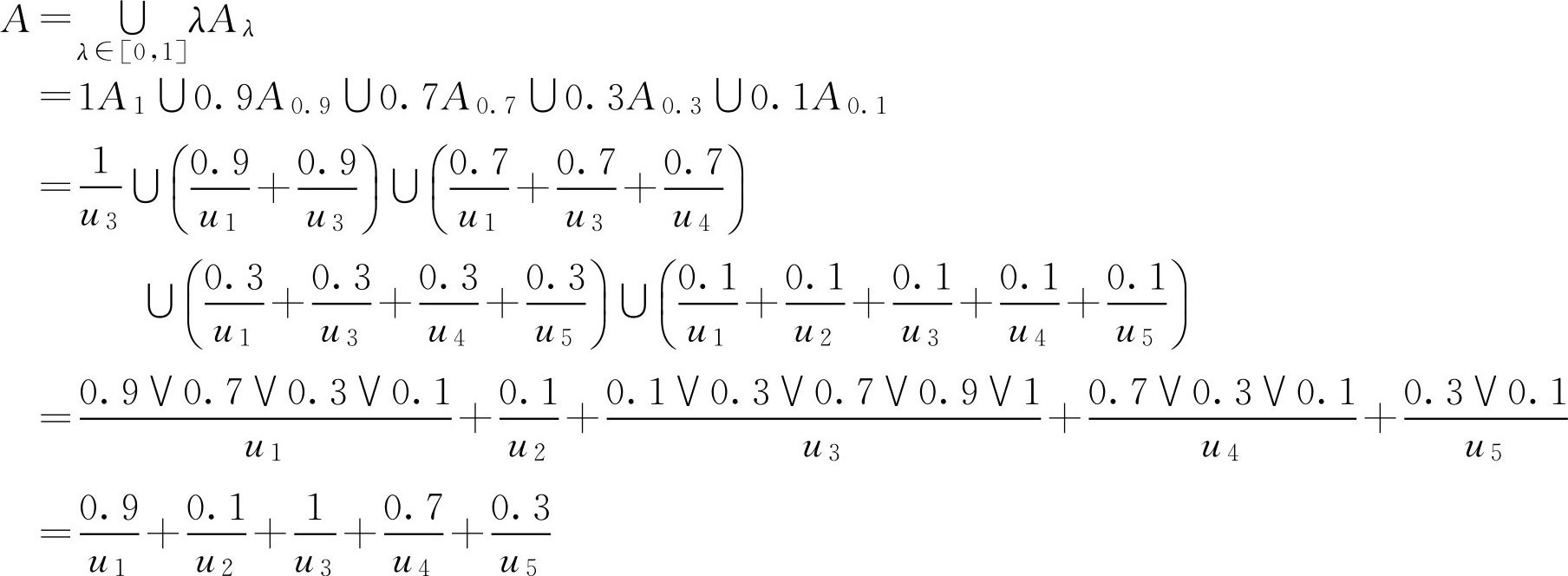
推论:
已知
F
集
A
的各
λ
截集为
A
λ
,
λ
∈[0,1],则
 u
∈
U
,有
u
∈
U
,有
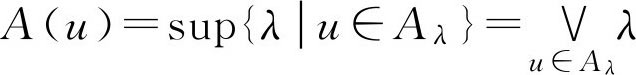
例2.9 设 U ={ u 1 , u 2 , u 3 , u 4 , u 5 },
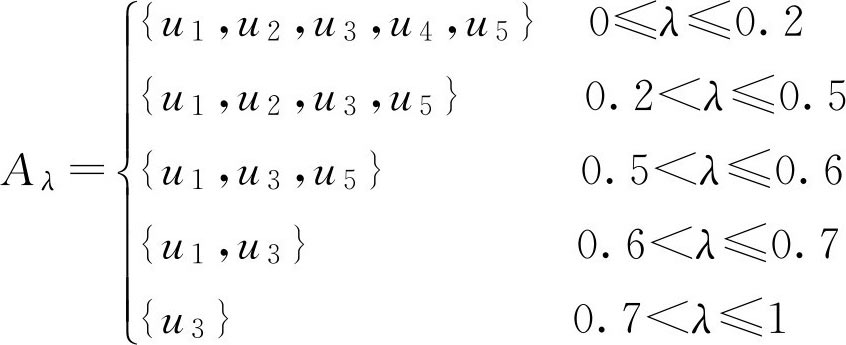
试求出 F 集 A 。
解:
由于含有元素 u 1 的一切 A λ 中,最大的 λ 值为0.7,所以 A ( u 1 )=0.7;含有元素 u 2 的一切 A λ 中,最大的 λ 值为0.5,所以 A ( u 2 )=0.5;类似可得 A ( u 3 )=1, A ( u 4 )=0.2, A ( u 5 )=0.6,于是 F 集 A 可表示为
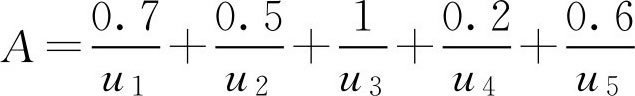
 2.1.6 模糊集的数量指标
2.1.6 模糊集的数量指标
2.1.2小节描述了 F 集之间的交、并、补运算,本小节给出刻画 F 集模糊程度的一些概念。
定义2.6 设 A ∈ F ( U ),记
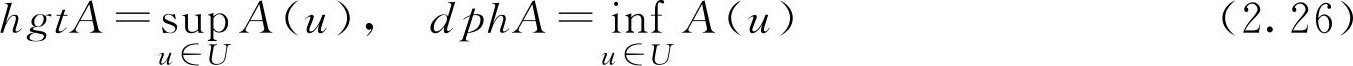
分别称为 F 集 A 的高度和深度。
F 集 A 的高度和深度反映了各元素隶属于 F 集的两个极值状态。高度反应的是“极大”方面的情况,深度反应的是“极小”方面的情况。对于有限论域上的 F 集,高度和深度反映了 F 集隶属函数的最大值与最小值,对于无限论域的情况,请看例2.11。
特别的,当 hgtA =1时,称 F 集 A 为正规 F 集,否则称为非正规 F 集。
若 F 集 A 为非正规 F 集,且存在 u 0 ∈ U ,使得 A ( u 0 )= hgtA ,则对任意的 u ∈ U ,令
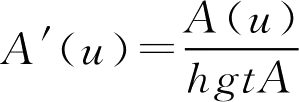 ,则
A’
化为了正规
F
集,这一过程称为
F
集的正规化。
,则
A’
化为了正规
F
集,这一过程称为
F
集的正规化。
例2.10
设论域
U
={
u
1
,
u
2
,
u
3
},且
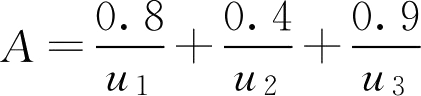 ,为
U
上的一非正规
F
集,求
hgtA
,
dphA
,并求
A
的正规化
F
集。
,为
U
上的一非正规
F
集,求
hgtA
,
dphA
,并求
A
的正规化
F
集。
解:
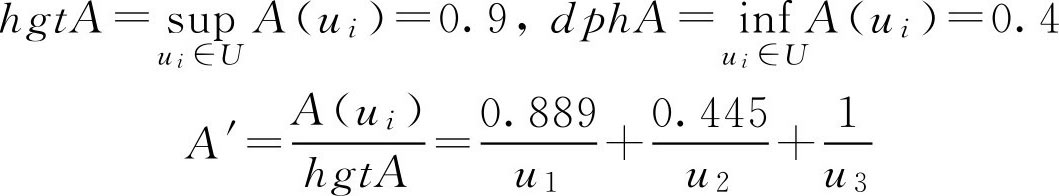
例2.11 设 A ∈ F ( R ), R 表示实数域, A 表示“所有比1大得多的实数”,其隶属函数表示如下,求 hgtA , dphA 。
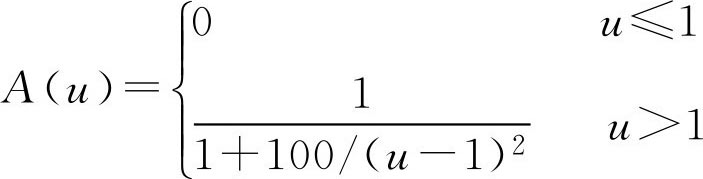
解:
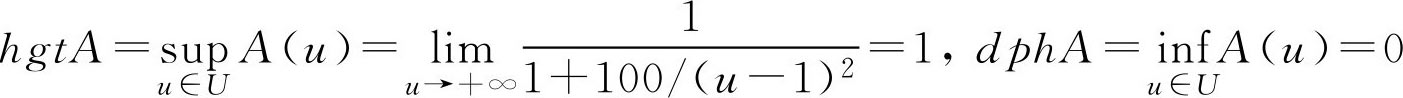
定义2.7 设论域 U ={ u 1 , u 2 ,…, u n }为有限论域, A ∈ F ( U ),记
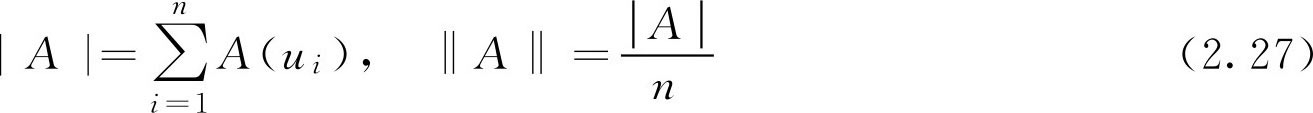
分别称为 F 集 A 的基数和相对基数。
注意: 本章后面的内容如不做特殊说明,将默认所有论域都为非空有限论域。
基数是反映 F 集 A 的“容量”的数量指标,如果 A 为普通集合,基数实际上就是集合元素的个数。相对基数则是描述 A 的“浓度”的指标。
例2.12 求例2.10中 F 集合 A 的基数与相对基数。
解:
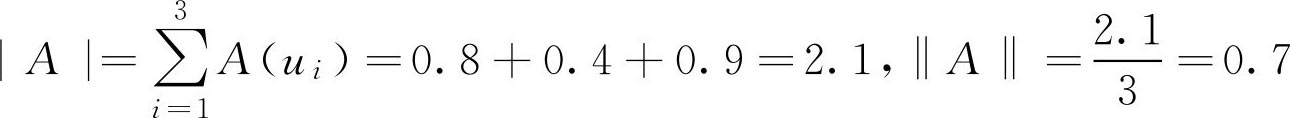
关于 F 集的高度、深度与相对基数,有下面的结论。
性质 设 A ∈ F ( U ),则下列性质成立:
(1) dphA ≤‖ A ‖≤ hgtA
(2)‖ A ‖+‖ A c ‖=1
(3) dphA =1- hgtA c
证明:
仅对(2)给出证明
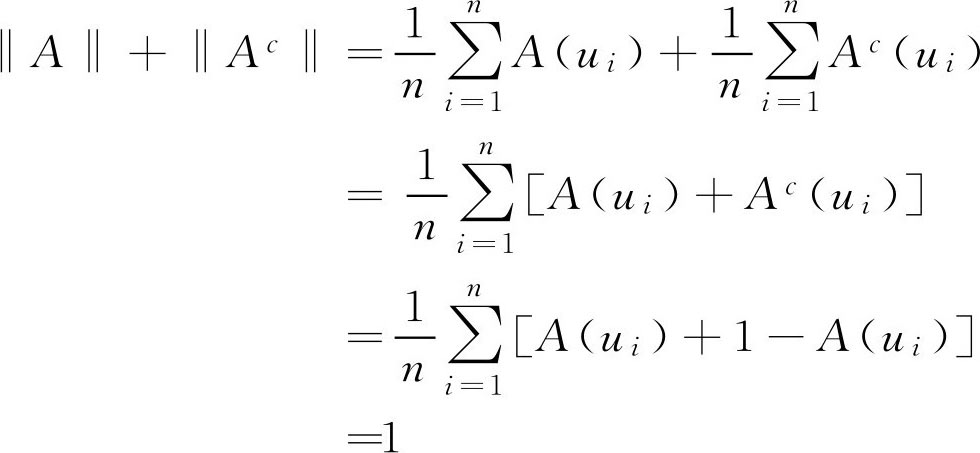
在利用模糊数学知识刻画某一实际问题中的模糊性概念时,常常需要用一个数量来表明这一模糊性概念的模糊程度,这个量就是模糊度。
定义2.8 若映射 d : F ( U )→[0,1]满足条件:
(1)
d
(
A
)=0
 A
为普通集合,
A
为普通集合,
(2)
 u
∈
U
,
d
(
A
)=1
u
∈
U
,
d
(
A
)=1
 A
(
u
)=0.5,
A
(
u
)=0.5,
(3)
 u
∈
U
,
A
,
B
∈
F
(
U
),若
B
(
u
)≤
A
(
u
)≤0.5或
B
(
u
)≥
A
(
u
)≥0.5,则有
d
(
A
)≥
d
(
B
),
u
∈
U
,
A
,
B
∈
F
(
U
),若
B
(
u
)≤
A
(
u
)≤0.5或
B
(
u
)≥
A
(
u
)≥0.5,则有
d
(
A
)≥
d
(
B
),
(4) d ( A )= d ( A c ),
则称映射 d 为 F ( U )上的一个模糊度, d ( A )称为 F 集 A 的模糊度。
定义2.8给出了一个关于模糊度的公理化定义,仔细分析可知,条件(1)表明只有 F 集才有模糊度,条件(2)和(3)表明元素对集合的隶属度越靠近0.5, F 集的状态越模糊,这种亦此亦彼的状态是最难决策的,条件(4)表明 F 集与它的补集具有相同的模糊度。但是,这一公理化的定义并不适用于计算,在实际应用中还需给出其具体的形式。下面我们给出一种可供计算的模糊度。
定义2.9 设 A ∈ F ( U ),记
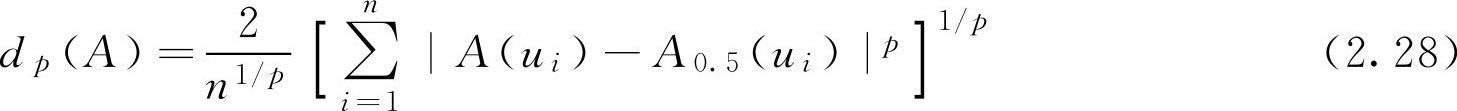
d p ( A )称为 A 的明科夫斯基(M inko w ski)模糊度( p 为正实数)。特别的,当 p =1, 2时的模糊度分别称为海明(Haming)模糊度和欧几里得(Euclid)模糊度(读者自行按照定义2.8证明定义2.9是否满足公理化定义)。
例2.13 已知 F 集

解:
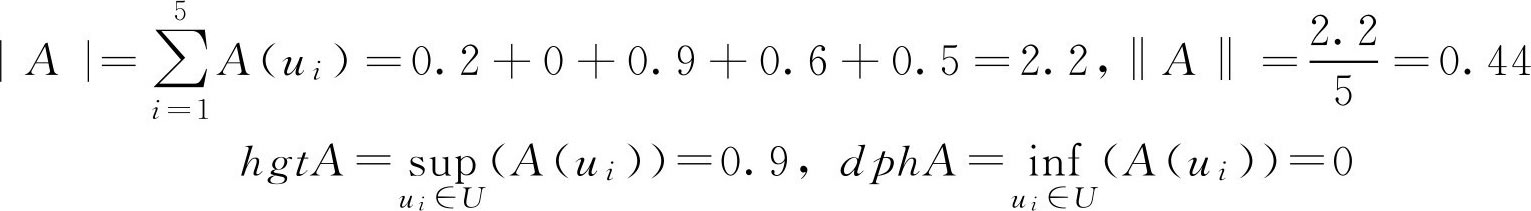
又因为
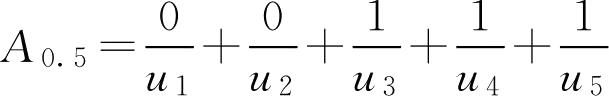 ,有
,有
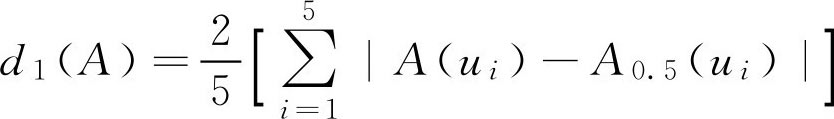
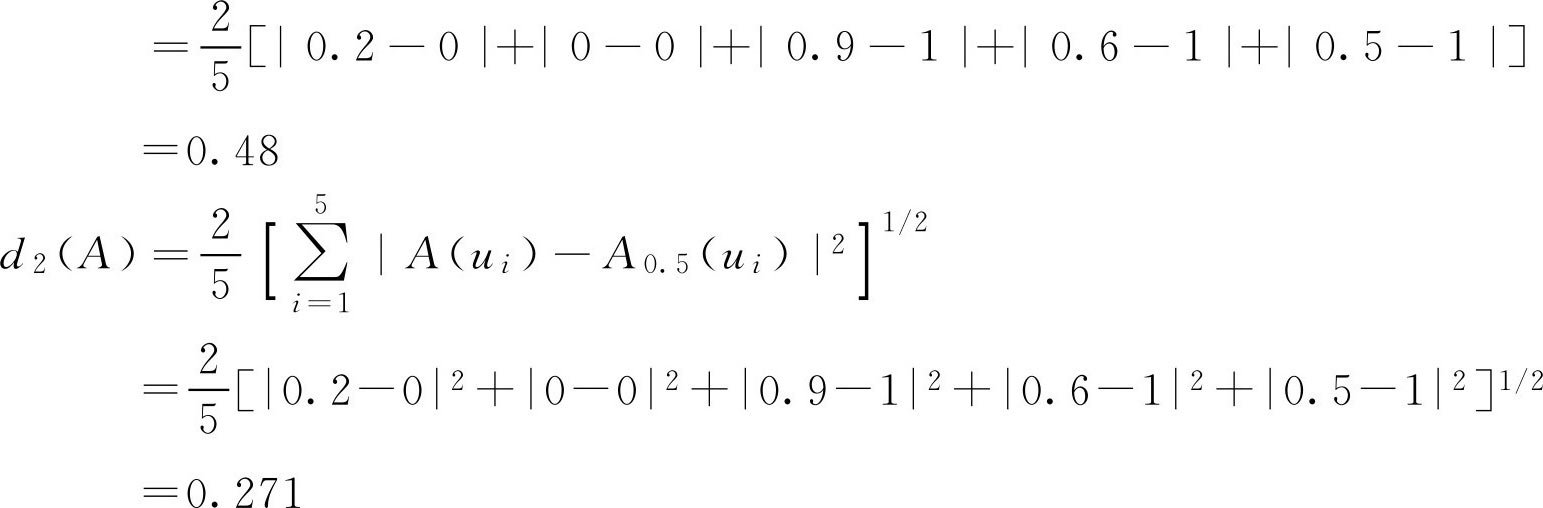
 2.1.7 模糊集的距离与贴近度
2.1.7 模糊集的距离与贴近度
研究清楚一个 F 集的数量指标后,我们开始引入两个 F 集间的关系。例如,如何去刻画两个 F 集间的相像程度呢,人们首先仿照两点间的距离公式给出了两个 F 集间的距离定义。
定义2.10 设 A , B ∈ F ( U ),记
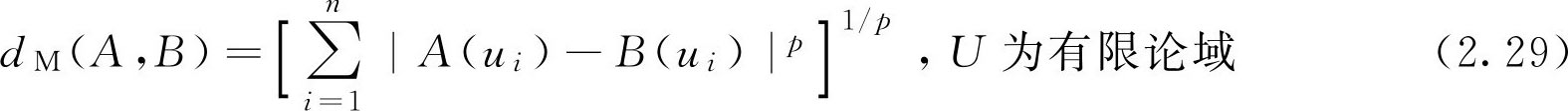
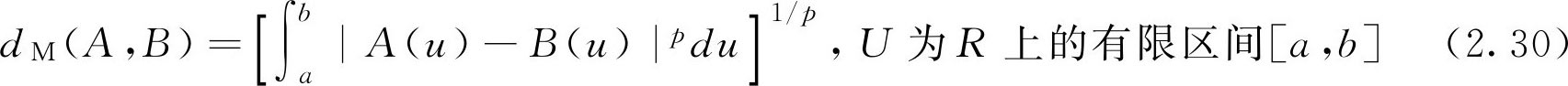
d M ( A , B )称为两个 F 集 A 与 B 的明科夫斯基(M inko w ski)距离。特别的,当 p =1,2时的距离分别称为海明(Haming)距离和欧几里得(Euclid)距离,分别记为 d H ( A , B )和 d E ( A , B )。
例2.14 已知论域 U ={ u 1 , u 2 , u 3 }, A , B ∈ F ( U ),具体表示如下
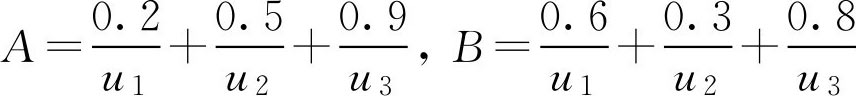
求 U 上两个 F 集的 d H ( A , B )和 d E ( A , B )距离。
解:
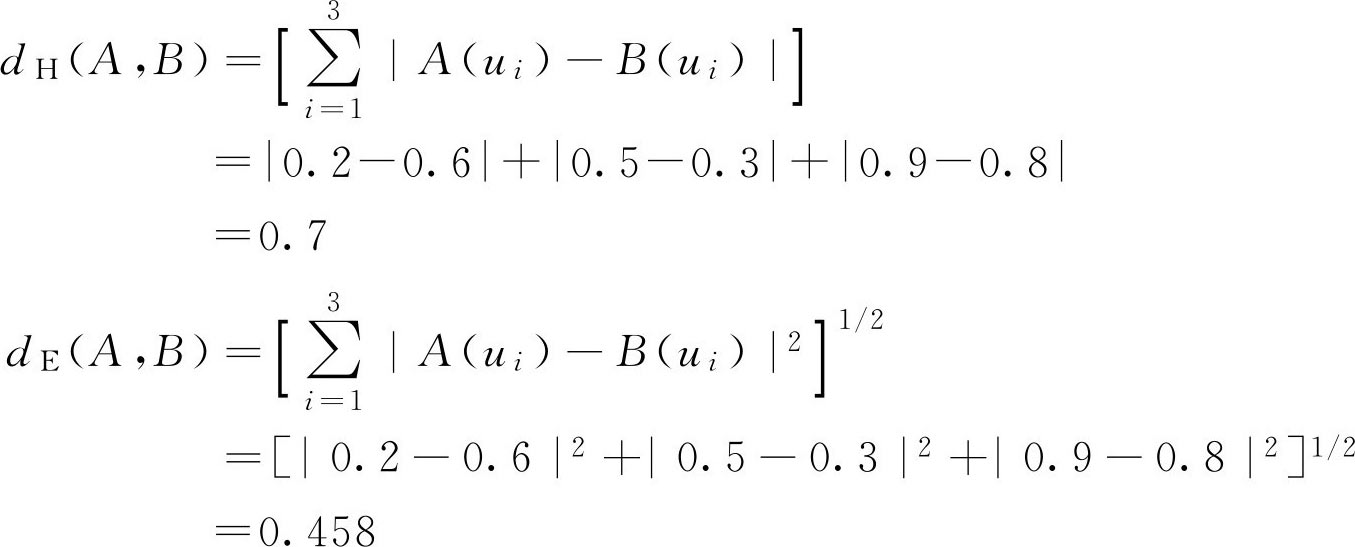
在实际应用中经常用到“相对海明距离”、“加权海明距离”和“加权相对海明距离”等,它们的定义分别为
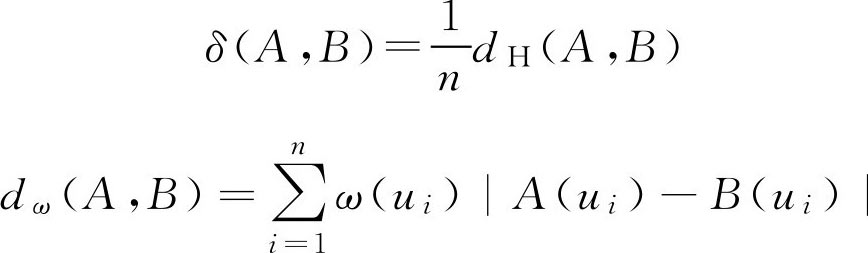
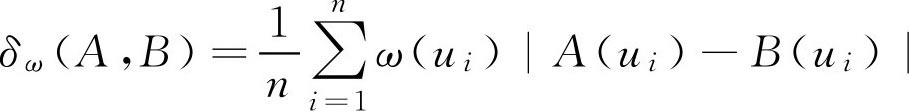
其中 ω ( u i )( i =1,2,…, n )是加于元素 u i 上的权重系数,一般都要求满足归一条件,即
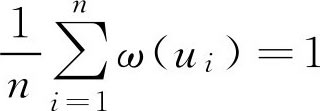
例2.15 求例2.14中两个 F 集在权向量为 ω =(1,1.8,0.2)下的 δ ( A , B ), d ω ( A , B )和 δ ω ( A , B )。
解:
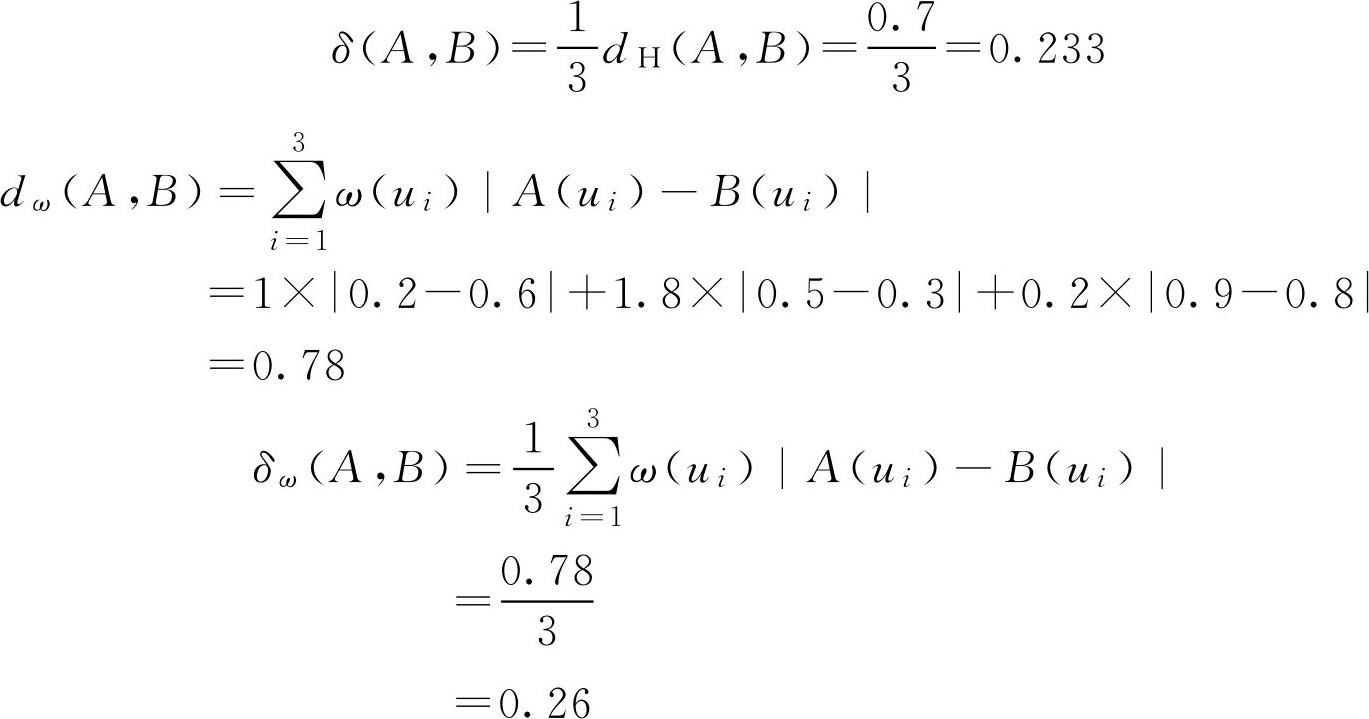
注意: 使用海明距离处理问题时,一定要对具体问题作具体分析,不能生搬硬套,否则有时得到的结论与实际情况不一致。比如选择人才,合格成绩是60分,现在有甲、乙两个人的成绩分别为58分和85分,将这些分数均除以100,作为隶属度,则两人的成绩与合格成绩间形成的海明距离分别为0.02和0.25,如果选取距离小的,则应该是甲,但事实上甲是不及格的,与实际情况不一致。
除了可以用距离来研究两个 F 集的相似程度外,人们还给出了一个新的概念,称之为贴近度。下面主要列举海明贴近度、欧几里得贴近度、黎曼贴近度和格贴近度。
定义2.11 设 A , B , C ∈ F ( U ),若映射
N : F ( U )× F ( U )→[0,1] (2.31)
满足条件:
(1) N ( A , B )= N ( B , A )
(2)
N
(
A
,
A
)=1,
N
(
U
,
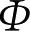 )=0
)=0
(3)若
A
 B
B
 C
,则
N
(
A
,
C
)≤
N
(
A
,
B
)∧
N
(
B
,
C
)
C
,则
N
(
A
,
C
)≤
N
(
A
,
B
)∧
N
(
B
,
C
)
则称 N ( A , B )为 F 集 A 与 B 的贴近度。 N 称为 F ( U )上的贴近度函数。
贴近度这个定义是原则性、公理化的概念,其具体规则视实际需要而定,为了满足应用上的需要,下面介绍几种常见的贴近度公式。
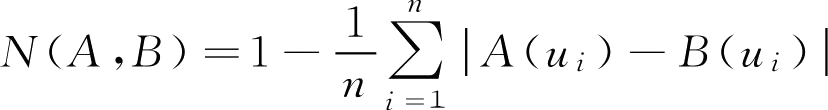 ,
U
为有限论域
,
U
为有限论域
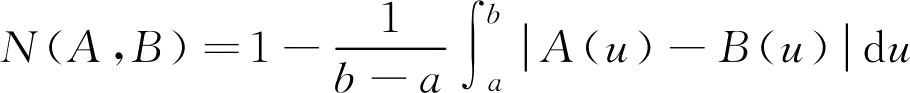 ,
U
为
R
上的有限区间[
a
,
b
]
,
U
为
R
上的有限区间[
a
,
b
]
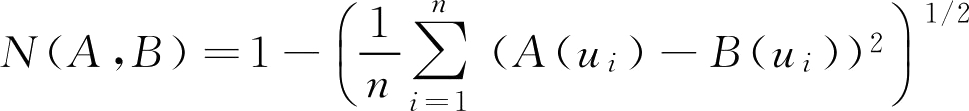 ,U为有限论域
,U为有限论域
 ,U为R上的有限区间[a,b]
,U为R上的有限区间[a,b]
若 U 为实数域,被积函数为黎曼可积,且广义积分收敛,则
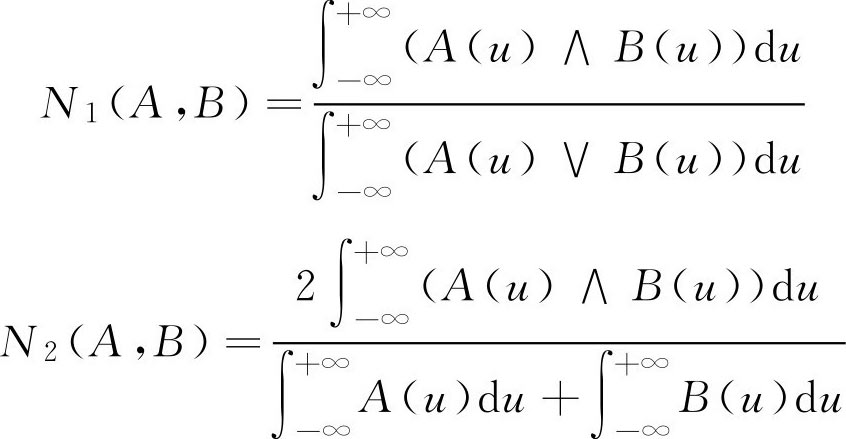
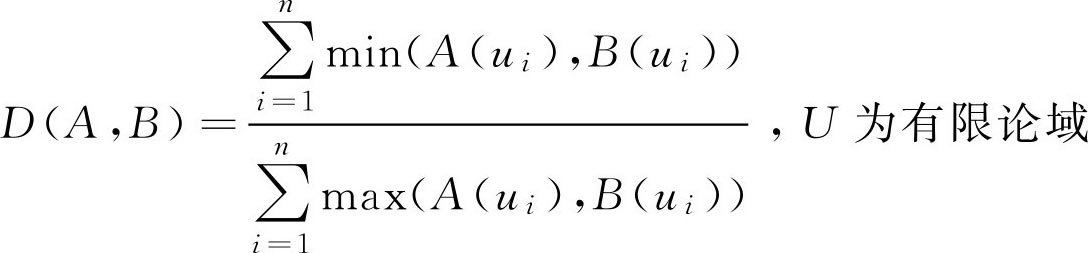
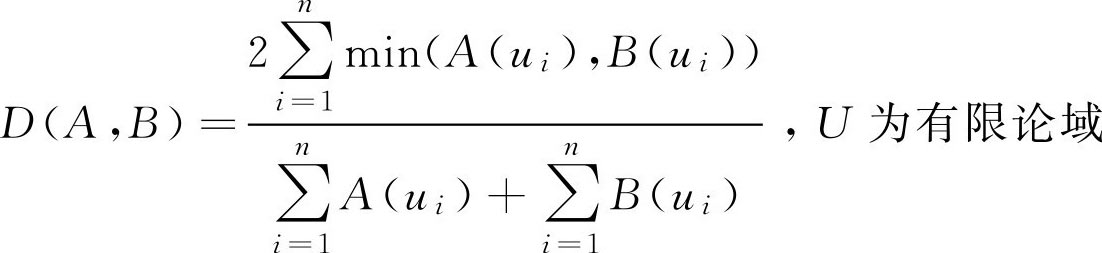
设 A , B ∈ F ( U ),则
D g ( A , B )=( A ° B )∧( A · B ) c (2.32)
是 F 集 A , B 的贴近度,称为 A , B 的格贴近度。
其中
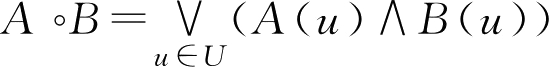 ,
,
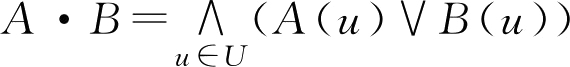 ,分别称为
F
集
A
,
B
的内积与外积。
,分别称为
F
集
A
,
B
的内积与外积。
其余的贴近度不再一一列举。实际上这些贴近度很难一般化地比较优劣,只有在实际应用中加以选择和修正。
例2.16 设 U =[0,100],其上的两个 F 集为 A , B ,且有
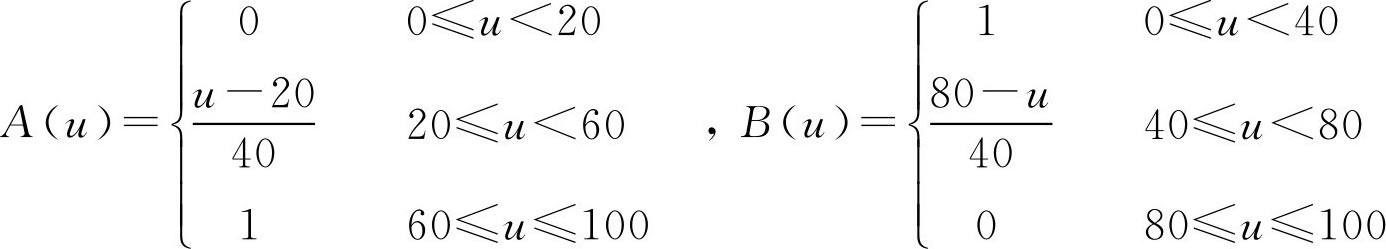
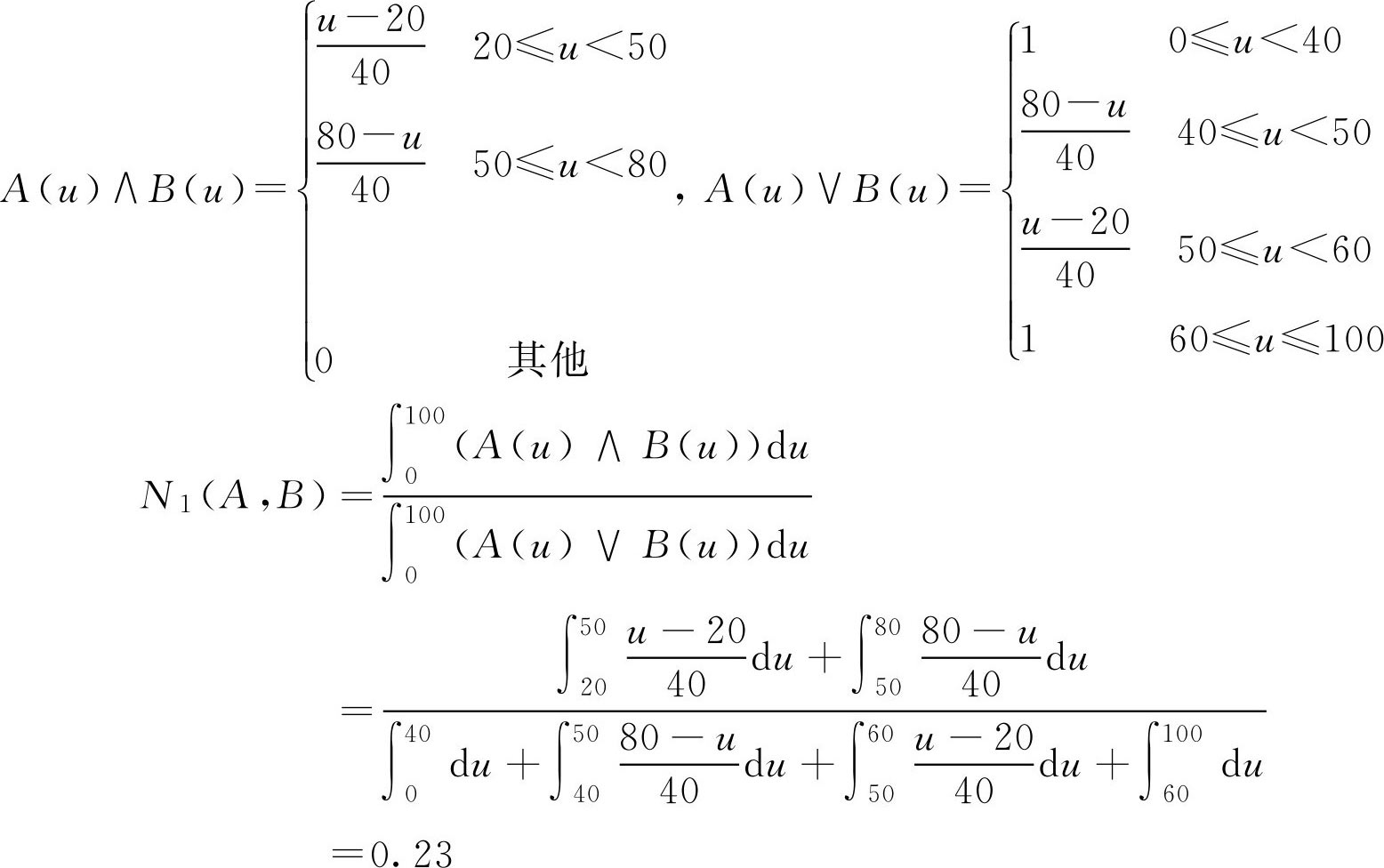
见图2.4,求黎曼贴近度 N 1 ( A , B )。
解: 不难求得隶属函数 A ( u )与 B ( u )的交点坐标为 u * =50,于是
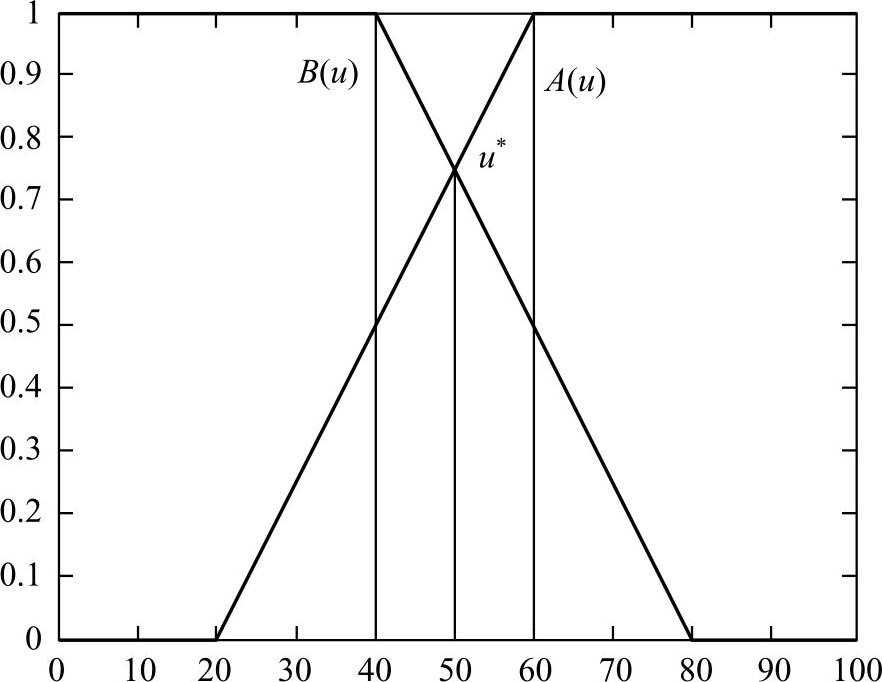
图2.4 F 集的隶属函数
例2.17 设论域 R 为实数域,正态 F 集 A , B 的隶属函数分别为
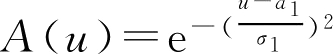 ,
,
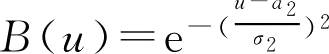 ,
σ
1
,
σ
2
>0,见图2.5,求
D
g
(
A
,
B
)。
,
σ
1
,
σ
2
>0,见图2.5,求
D
g
(
A
,
B
)。
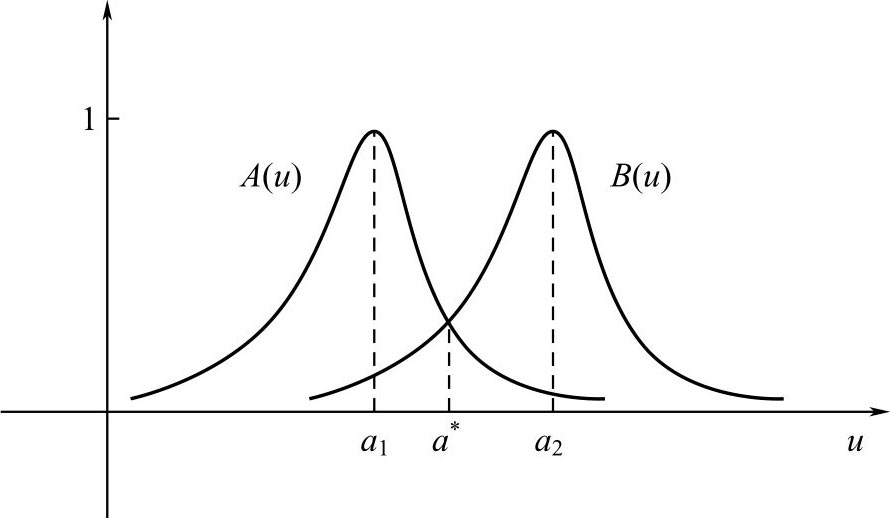
图2.5 正态 F 集隶属函数
解:
对上述两个隶属函数,观察图2.5,设交点为 a * ,有
若
u
≤
a
*
,
B
(
u
)≤
A
(
u
),则
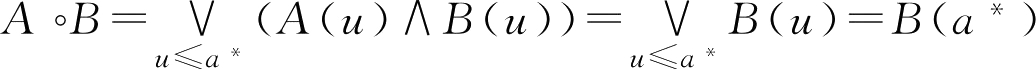 。
。
若
u
>
a
*
,
A
(
u
)≤
B
(
u
),则
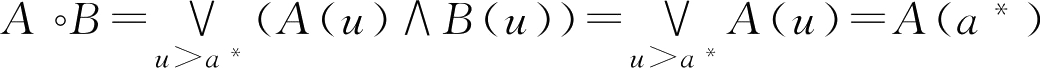 。
。
可见,内积 A ° B 是 A ( u )与 B ( u )相等的值。故可令 A ( u )= B ( u )求 a * 。
由
 ,求得
,求得
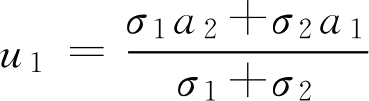 ,
,
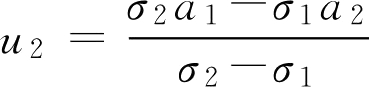 (舍去),选
u
1
=
a
*
。
(舍去),选
u
1
=
a
*
。
可得
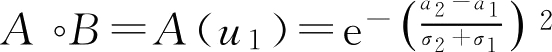 。同理可得
。同理可得
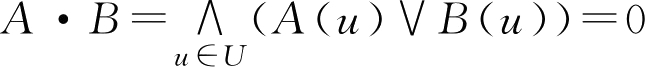 。
。
由格贴近度公式,得
 。
。
注意: 当 a 1 = a 2 时, D g ( A , B )=1,这表明格贴近度只是注重了两个 F 集的峰值点位置,并没有考虑到 σ 1 ≠ σ 2 这一事实。
一般来说,贴近度主要应用于模糊模式识别领域,本部分内容只是对贴近度做概念和公式上的分析,其具体应用将在第5章详细讲解。