





铆工在样台进行放样作业时,必须掌握一套熟练的几何作图方法,才能把构件的形状正确地绘制在工件上。而正确放样的基础是几何作图。本节主要介绍铆工常用的基本几何作图方法。
已知 AB 直线,作一平行于 AB 的直线 CD ,两条平行线间距为 R 。作法如图2-93所示。
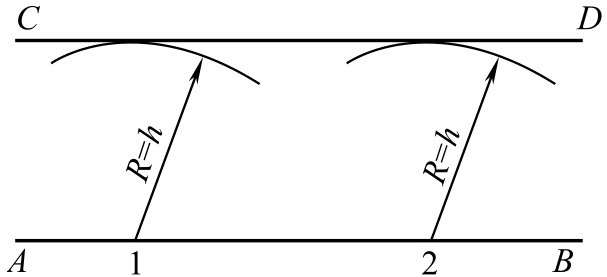
图2-93 平行线作法
①在直线 AB 上任取两点1、2为圆心,以 h 为半径分别画圆弧。
②作两圆弧的公切线 CD ,此直线 CD 即为所求。
作法如图2-94所示。
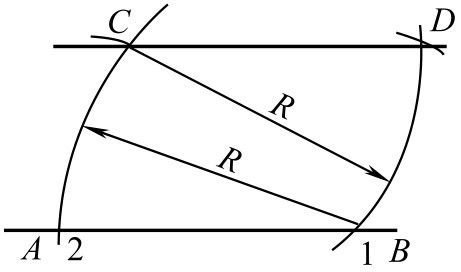
图2-94 平行线作法
①任取长度 R 为半径, C 为圆心作圆弧,交直线 AB 于1点。
②以1点为圆心, R 为半径作圆弧,交直线 AB 于2点。
③以1点为圆心,取 C 、2两点距离为半径画圆弧,得交点 D 。
④连接 CD 即为所求。
已知 AB 直线上一点 O 的垂线作法如图2-95所示。
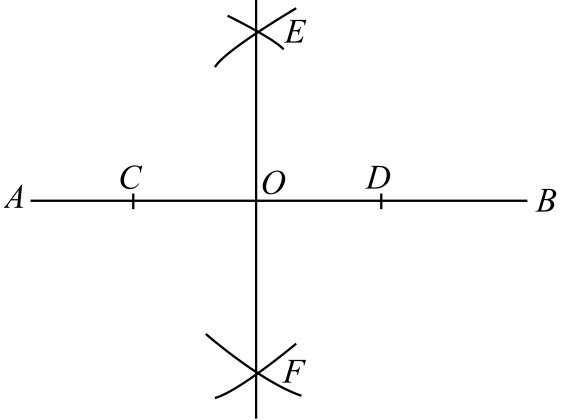
图2-95 垂直线作法
①以 O 为圆心,任意长为半径画弧,在 AB 直线上交于 C 、 D 两点。
②分别以 C 、 D 为圆心,以任意半径画弧,相交于 E 、 F 两点。
③连接 FE ,即为垂直于 AB 并过 O 点的直线。就是通常所说的十字线。
1)作法1如图2-96所示。
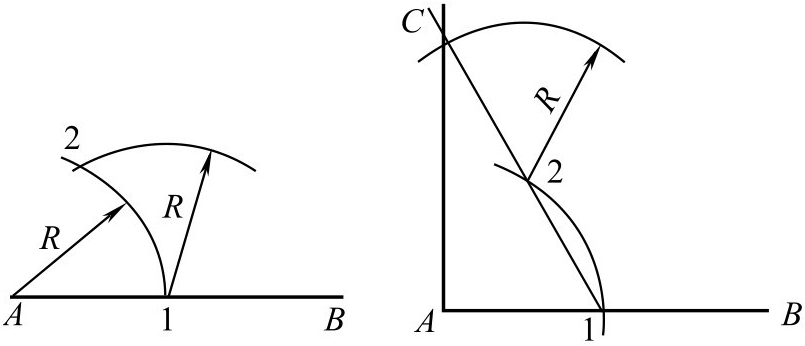
图2-96 垂线作法1
①以 A 点为圆心,任意长尺寸为半径画弧,交 AB 线于1点。
②以1点为圆心, R 为半径画弧,交前弧于2点,连接1—2并延长。
③以2点为圆心, R 为半径画弧,交1—2延长线于 C 点,连接 CA 即为所求。
2)作法2如图2-97所示。
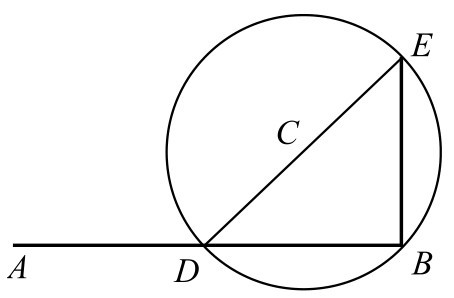
图2-97 垂线作法2
①在线外任取一点 C 为圆心,以 CB 为半径作圆,交直线 AB 于 D 点。
②连接 CD 并延长交圆于 E 点,连接 BE 即为所求的垂线。
已知线段 AB ,作 AB 垂直平分线 CD ,如图2-98所示。
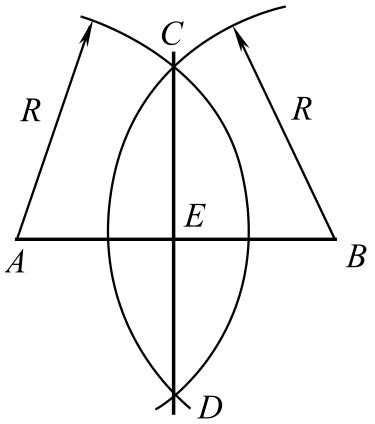
图2-98 二等分线作法
①分别以直线的两端点 A 、 B 为圆心,取大于 AB 之长为半径,作弧交于 C 及 D 两点。
②连接 CD 交直线 AB 于 E ,即 AE = EB 。 CD 又称为 AB 的垂直平分线。
①试分法 对已知线段可凭目测用分规进行等分,如图2-99所示。
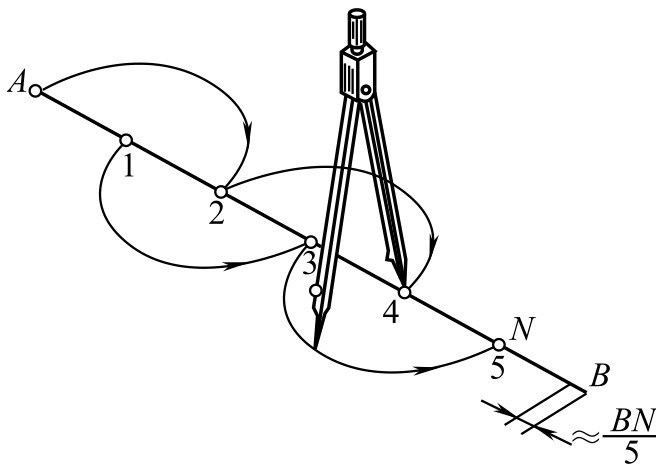
图2-99 试分法等分线段
②平行线法 已知线段 AB ,求作任意等分(如5等分)。其作图方法如图2-100所示。作图步骤如下:
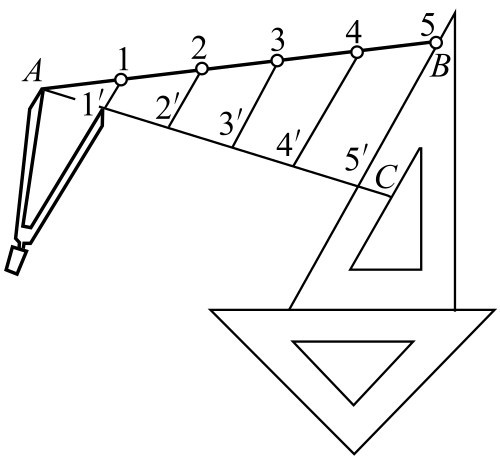
图2-100 用平行线法等分线段
a.过端点 A 作直线 AC ,与已知线段 AB 成任意锐角;
b.用分规在 AC 上任意取相等长度得1′、2′、3′、4′、5′各等分点;
c.连接5′ B ,并分别过4′、3′、2′、1′各点作5′ B 的平行线,在 AB 线上即得4、3、2、1各等分点。
铆工操作中,直角通常是用来检验钢板是否规矩(俗称为规方),以及检验所画的垂直线和角度是否正确。常用的画直角方法有以下几种。
①利用勾股弦定理(即勾3、股4、弦5)画直角,如图2-101(a)所示。
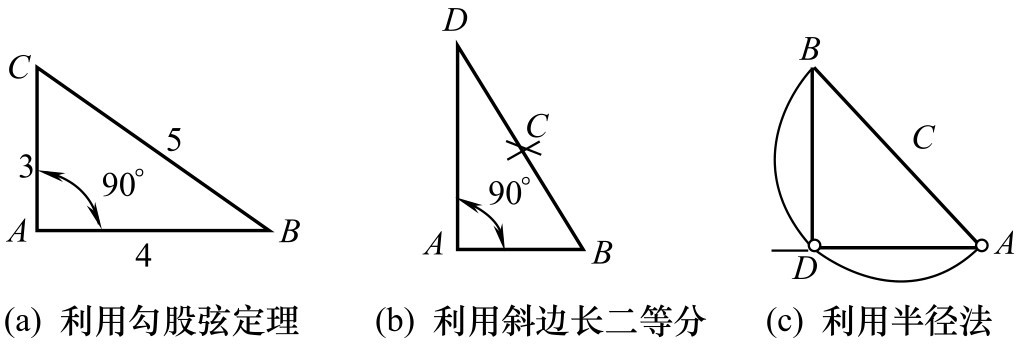
图2-101 直角的画法
②利用斜边长二等分画直角,如图2-101(b)所示。
③利用半径法画直角,如图2-101(c)所示。
如图2-102所示的近似法。若作一角等于50°,其步骤如下。
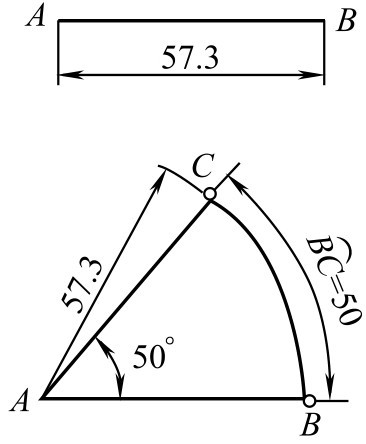
图2-102 任意角的画法
①画线段 AB 等于57.3mm;
②以 A 为圆心, AB 为半径画圆弧;
③在圆弧上每取1mm的弧长,其所对的圆心角为1°(因为圆周长
L
=2π
R
,其中
R
为圆的半径,所以2×3.1416×57.3=360.0159),这样截取
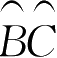 等于50mm,则∠
CAB
即为50°。为减小角度误差,在放样时可根据结构尺寸用
n
倍(放大系数)57.3mm为半径画圆,这时该圆上的
n
倍弧长所对的圆心角为1°。
等于50mm,则∠
CAB
即为50°。为减小角度误差,在放样时可根据结构尺寸用
n
倍(放大系数)57.3mm为半径画圆,这时该圆上的
n
倍弧长所对的圆心角为1°。
如图2-103所示,已知∠ ABC ,求作一角等于已知角。其步骤如下。
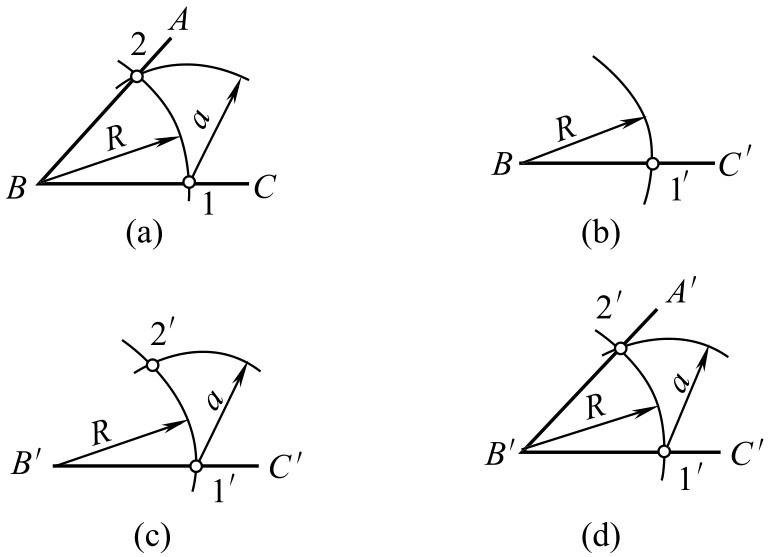
图2-103 已知角的三角形画法
①以 B 点为圆心,取 R 长为半径画圆弧,交两边于1、2点[图2-103(a)]。
②另作一条直线 B ′ C ′,以 B ′点为圆心, R 为半径,画圆弧交 B ′ C ′于1′点[图2-103(b)]。
③以1′点为圆心,用已知角上的1—2弦长为半径,画弧交前弧于2′点[图2-103(c)]。
④连接2′点与 B ′点,则∠2′ B ′1′=∠ ABC [图2-103(d)]。
作法如图2-104所示。
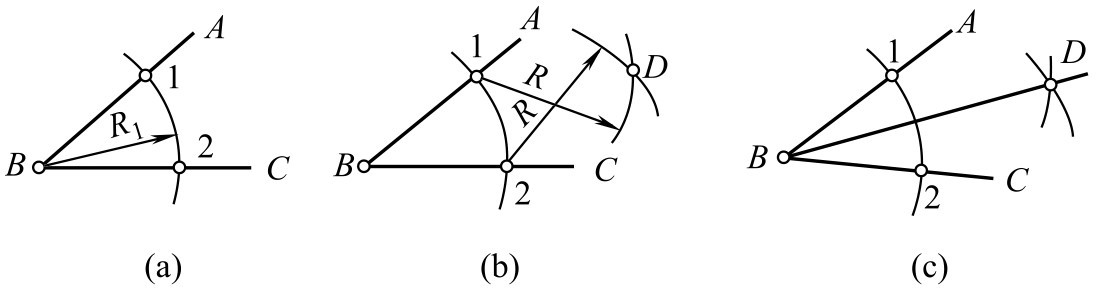
图2-104 角的二等分画法
①以 B 点为圆心,任意长度为半径画圆弧,交角的两边于1、2两点[图2-104(a)]。
②分别以1、2两点为圆心, R 为半径画弧相交于 D 点[图2-104(b)]。
③连接 B 、 D 两点,则 BD 线分∠ ABC 为二等分[图2-104(c)]。
作法如图2-105所示。
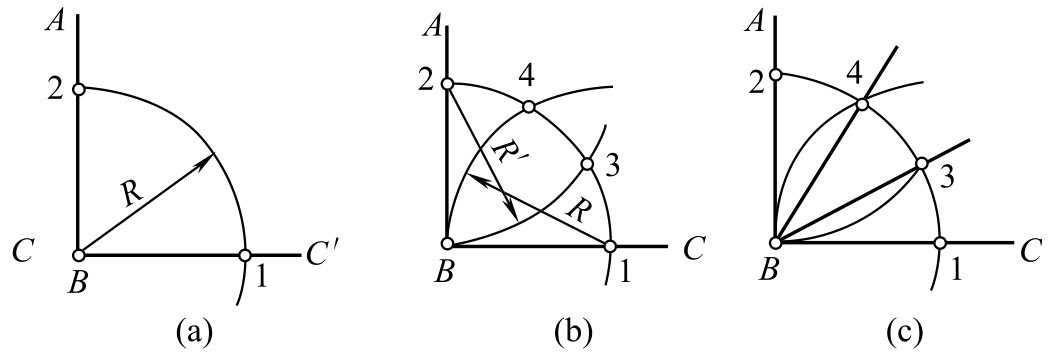
图2-105 三等分直角的画法
①以 B 点为圆心, R 为半径画圆弧,交直角两边于1、2两点。
②以1、2两点为圆心, R 为半径,分别画两弧交前弧于3、4两点。
③连接 B 、3和 B 、4,便为直角∠ ABC 的三等分。
以三等分为例,如图2-106所示。作图步骤如下。
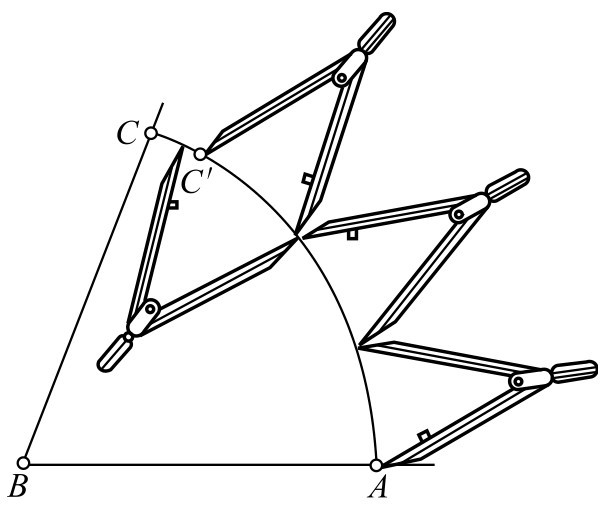
图2-106 角度试分法
①以角顶点 B 为圆心,以适当长度(稍大一些)为半径,画圆弧 AC ;
②目测并调节分规,约为 AC 长的1/3,一次截取后,再进行调整,直至将 AC 分尽;
③将角顶点 B 与各分点连接,即将角等分。
①用圆的半径六等分圆周。当已知正六边形对角距离(即外圆直径)时,可用此法画出正六边形,如图2-107所示。
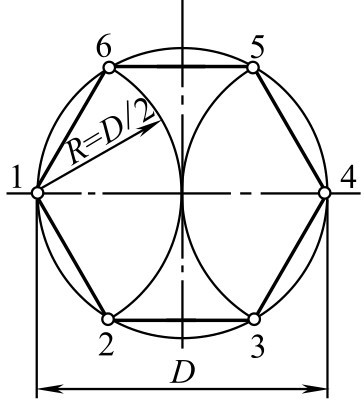
图2-107 用半径6等分圆周
②用丁字尺、三角板配合作圆的内接、外切正六边形,如图2-108所示。
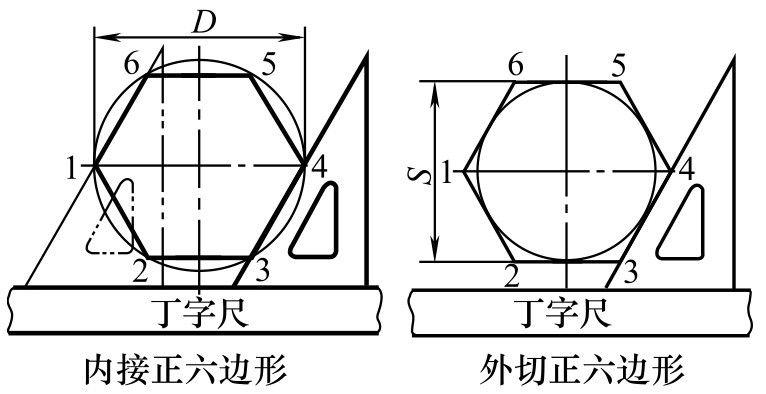
图2-108 圆的内接、外切正六边形画法
①平分 OB 得其中点 P 。
②在 AB 上取 PH = PC ,得点 H 。
③以 CH 为边长等分圆周,得 E 、 F 、 G 、 L 等分点,依次连接,即得正五边形,如图2-109所示。
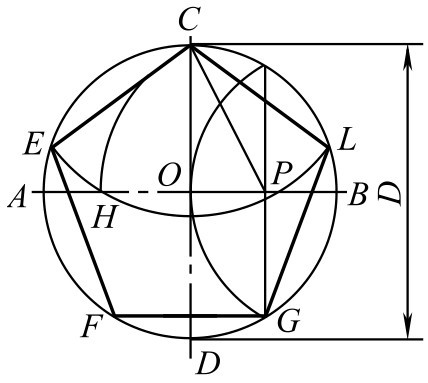
图2-109 正五边形画法
斜度是指一直线(或平面)对另一直线(或平面)的倾斜程度。在图2-110(a)中, AB 边对 AC 边的斜度用 BC 边与 AC 边的比值表示,即 AB 对 AC 的斜度= BC / AC =tan α =1: n 。
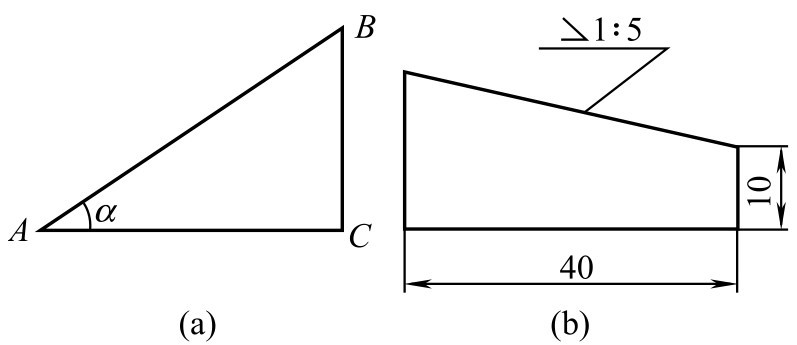
图2-110 斜度及其标注
斜度的标注用符号“∠1: n ”表示,如图2-110(b)所示。
其作图过程如图2-111所示,在
CD
上取一个单位长
CD
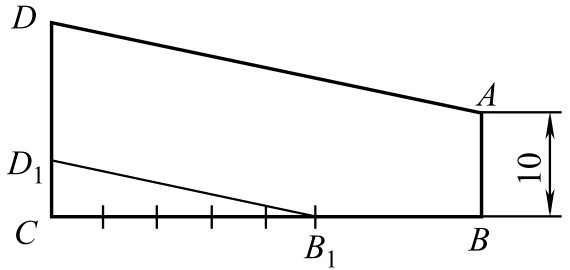
图2-111 斜度的作图步骤
斜度符号按图2-112所示绘制,其符号中斜线所示的方向应与斜度方向一致。
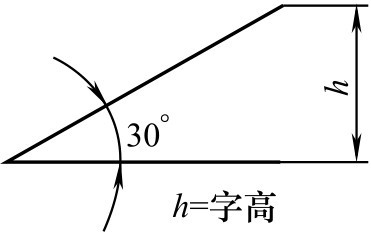
图2-112 斜度符号
指正圆锥底圆直径与锥高之比。若是锥台,则为两底圆直径之差与锥台高度之比,如图2-113(a)所示。
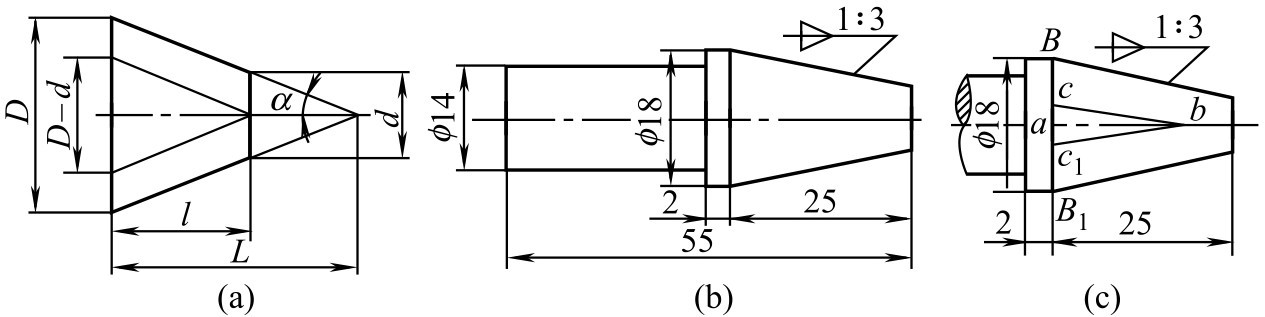
图2-113 锥度、锥度标注及作图步骤
锥度= D / L =( D - d )/ l =2tan α =1: n
锥度的标注用符号“
 1:
n
”表示,要标注在基准线上,锥度符号方向应与圆锥方向一致,如图2-113(b)、(c)所示。锥度符号按图2-114所示绘制。
1:
n
”表示,要标注在基准线上,锥度符号方向应与圆锥方向一致,如图2-113(b)、(c)所示。锥度符号按图2-114所示绘制。
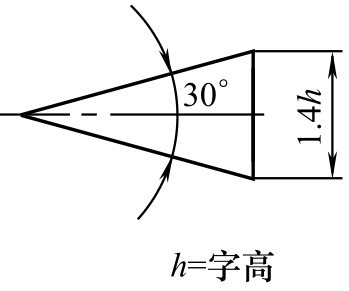
图2-114 锥度的图形符号
锥度的作图过程如图2-113(c)所示。取 ac = ac 1 ,在水平轴线上取 ab =3 cc 1 ,连接 cb 、 c 1 b ,得1:3的锥度辅助线;过 B 、 B 1 作 cb 和 c 1 b 的平行线,即为所求锥度。
圆弧连接是指用已知半径的圆弧,光滑地连接两已知线段的作图方法。如图2-115所示,圆弧连接的实质就是使连接圆弧与相邻线段相切,以达到光滑连接的目的。
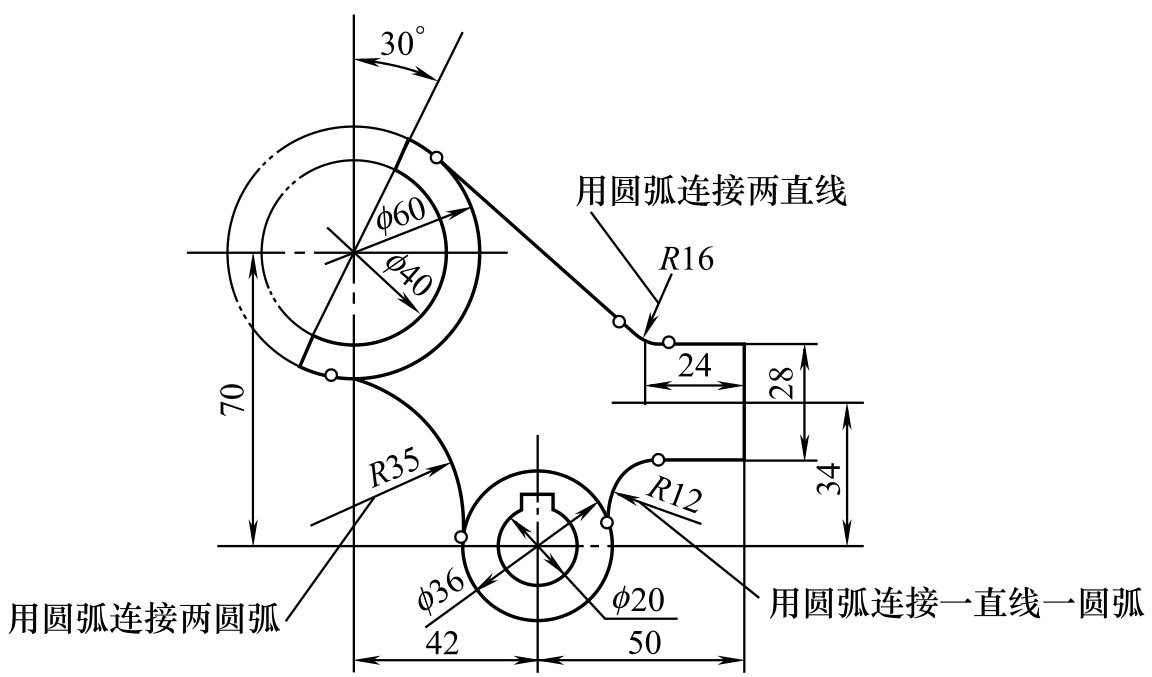
图2-115 圆弧连接
①连接弧圆心的轨迹为一平行于已知直线的直线。两直线间的垂直距离为连接弧的半径 R 。
②由圆心向已知直线作垂线,其垂足即为切点,如图2-116所示。
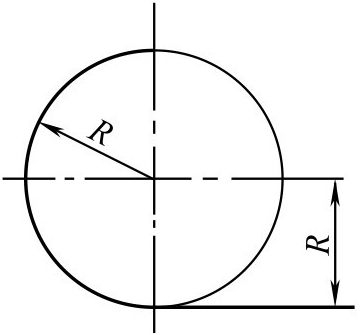
图2-116 圆弧与直线连接
①连接弧圆心的轨迹为已知圆弧的同心圆,该圆的半径为两圆弧半径之和( R 1 + R )。
②两圆心的连线与已知圆弧的交点即为切点,如图2-117所示。
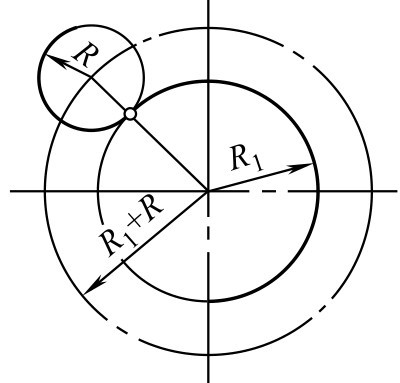
图2-117 圆弧与圆弧连接(外切)
①连接弧圆心的轨迹为已知圆弧的同心圆,该圆的半径为两圆弧半径之差( R 1 - R )。
②两圆心连线的延长线与已知圆弧的交点即为切点,如图2-118所示。
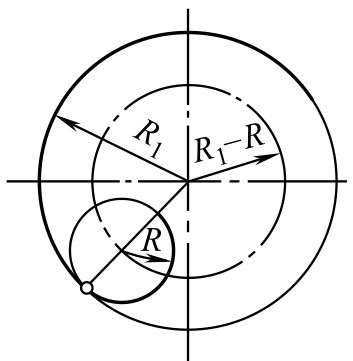
图2-118 圆弧与圆弧连接(内切)
①作与已知角两边分别相距为 R 的平行线,交点 O 即为连接弧圆心。
②自 O 点分别向已知角两边作垂线,垂足 M 、 N 即为切点。
③以 O 为圆心, R 为半径在两切点 M 、 N 之间画连接圆弧即为所求,如图2-119所示。
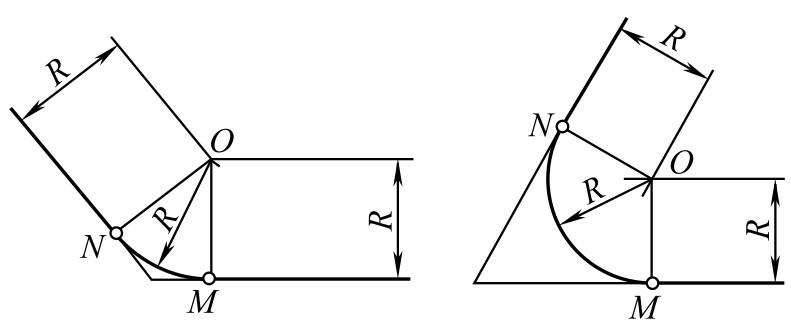
图2-119 圆弧连接锐角或钝角
①以角顶为圆心, R 为半径画弧,交直角两边于 M 、 N 。
②以 M 、 N 为圆心, R 为半径画弧相交得连接弧圆心 O 。
③以 O 为圆心, R 为半径在 M 、 N 间画连接圆弧即为所求,如图2-120所示。
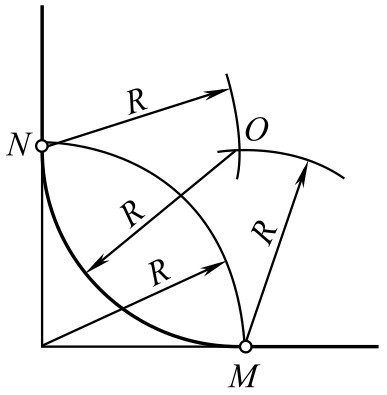
图2-120 圆弧连接直角的两边
①已知连接圆弧的半径为 R ,将此圆弧外切于圆心为 O 1 ,半径为 R 1 的圆弧和直线Ⅰ。
②作直线Ⅱ平行于直线Ⅰ(其间距为 R );再作已知圆弧的同心圆(半径为 R 1 + R )与直线Ⅱ相交于 O 点。
③作 OA 垂直于直线Ⅰ;连接 OO 1 交已知圆弧于 B , A 、 B 即为切点。
④以 O 为圆心, R 为半径画圆弧,连接直线Ⅰ和圆弧 O 1 于 A 、 B 即完成作图,如图2-121所示。
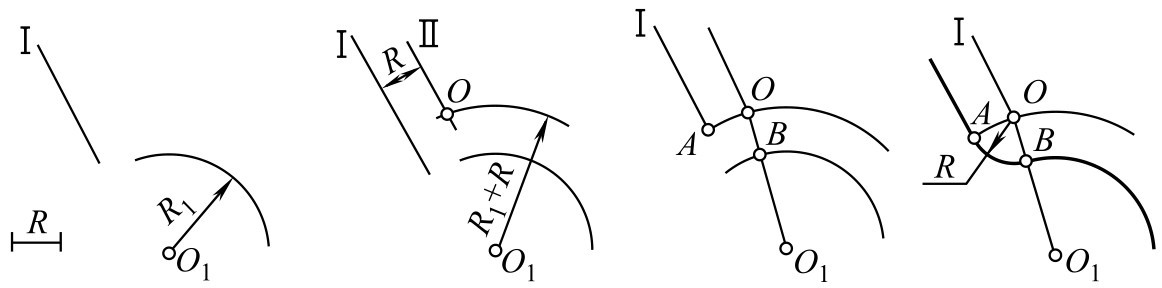
图2-121 直线和圆弧间的圆弧连接
①已知连接圆弧的半径为 R ,将此圆弧同时外切于圆心为 O 1 、 O 2 ,半径为 R 1 、 R 2 的圆弧。
②分别以( R 1 + R )及( R 2 + R )为半径, O 1 、 O 2 为圆心,画圆弧相交于 O 点。
③连接 OO 1 交已知圆弧于 A 点,连接 OO 2 交已知圆弧于 B 点, A 、 B 即为切点。
④以 O 为圆心, R 为半径作圆弧,连接已知圆弧于 A 、 B 即完成作图,如图2-122所示。

图2-122 两圆弧间的圆弧连接
①已知连接圆弧的半径为 R ,将此圆弧同时内切于圆心为 O 1 、 O 2 ,半径为 R 1 , R 2 的圆弧。
a.分别以( R - R 1 )和( R - R 2 )为半径, O 1 和 O 2 为圆心,画圆弧相交于 O 点。
b.连接 OO 1 并延长,交已知圆弧于 A 点;连接 OO 2 并延长,交已知圆弧于 B 点, A 、 B 即为切点。
c.以 O 点为圆心, R 为半径作圆弧,连接已知圆弧于 A 、 B 即完成作图,如图2-123所示。

图2-123 两圆弧间内连接(一)
②已知连接圆弧的半径为 R ,将此圆弧外切于圆心为 O 1 点,半径为 R 1 的圆;同时又内切于圆心为 O 2 ,半径为 R 2 的圆弧。
a.分别以( R 1 + R )及( R 2 - R )为半径, O 1 O 2 为圆心,画圆弧相交于 O 点。
b.连接 OO 1 交已知圆弧于 A 点;连接 OO 1 并延长交已知圆弧于 B 点, A 、 B 即为切点。
c.以 O 点为圆心, R 为半径作圆弧,连接已知圆弧于 A 、 B 即完成作图,如图2-124所示。
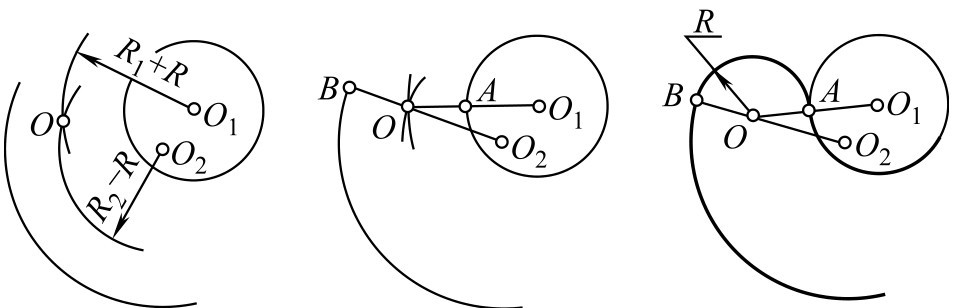
图2-124 两圆弧间内连接(二)
作圆弧的切线时,通常借助于三角板作图。作切线的关键是求切点。其作图步骤是首先初步定出切线的位置,然后准确找出切点,最后作出切线。
①过定点作已知圆的一条切线,如图2-125(a)所示。
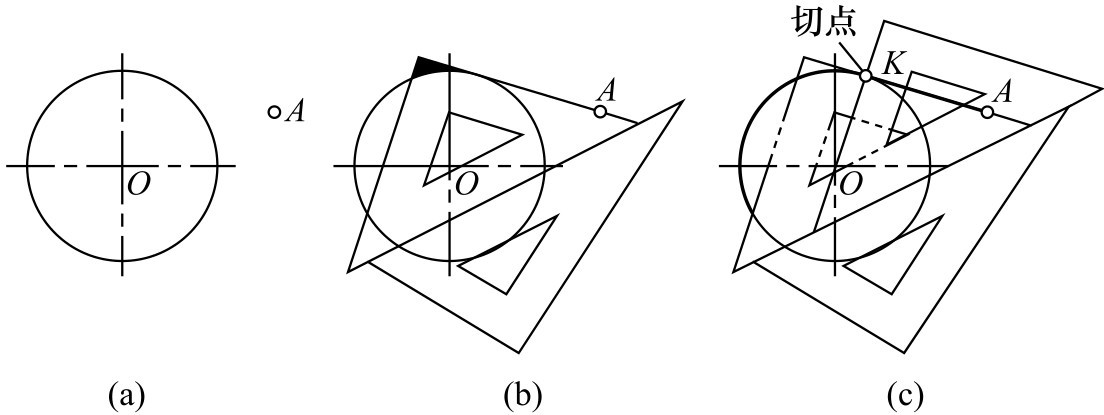
图2-125 过定点作圆的切线
a.把第一块三角板的一直角边放在过点 A 且与已知圆相切的位置上,然后将第二块三角板与第一块三角板的斜边靠紧,如图2-125(b)所示。
b.沿第二块三角板推动第一块三角板,直至另一直角边通过圆心时作直线,其与圆相交得切点 K ,连接 A 、 K 即作出切线,如图2-125(c)所示。
②作两圆的一条内公切线,如图2-126(a)所示。
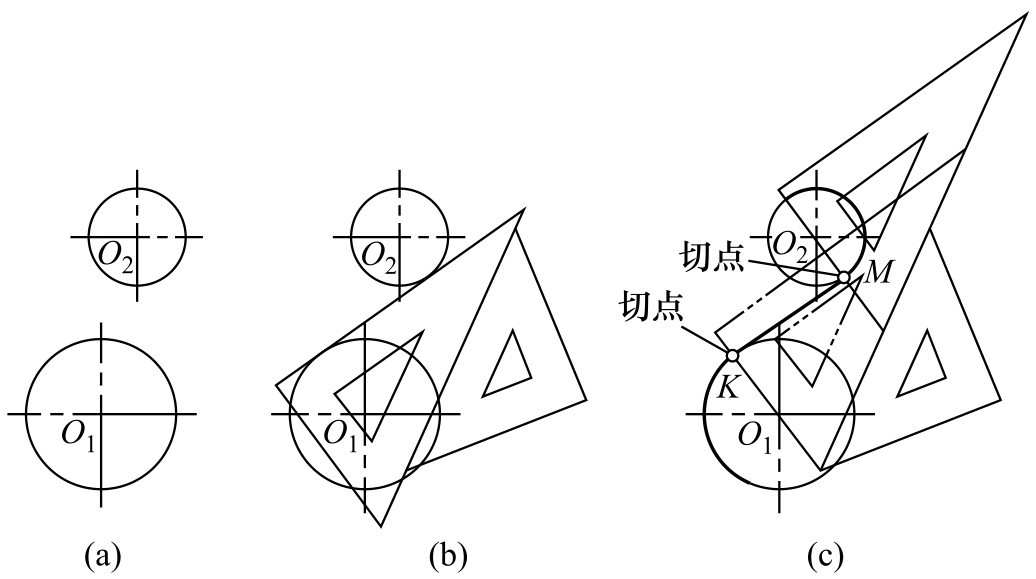
图2-126 作两圆的内公切线
a.把第一块三角板的一直角边放在内公切线的位置上,然后将第二块三角板与第一块三角板的斜边靠紧,如图2-126(b)所示。
b.沿第二块三角板推动第一块三角板,当另一直角边通过圆心 O 1 、 O 2 时,分别作直线,与圆相交得 K 、 M 点,连接 K 、 M 即作出内公切线,如图2-126(c)所示。
①以椭圆中心为圆心,分别以长轴、短轴长度为直径,作两个同心圆。
②过圆心作任意直线交大圆于1、2两点,交小圆于3、4两点,分别过1、2点引垂线,过3、4点引水平线,它们的交点 a 、 b 即为椭圆上的点。
③按步骤②的方法,重复作图,求出椭圆上一系列的点。
④用曲线板光滑地连接诸点即得椭圆,如图2-127所示。
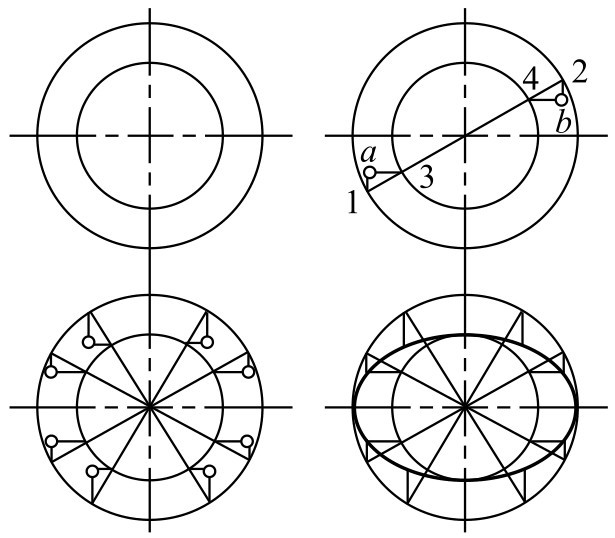
图2-127 同心圆画法
①画出长轴 AB 和短轴 CD 。连接 AC 。
②以 O 点为圆心, OA 为半径画弧 AE 。再以 C 点为圆心, CE 为半径画弧 EF 。
③作 AF 的垂直平分线,与 AB 交于1点,与 CD 交于2。取1、2的对称点3、4。
④分别以2、4为圆心,2 C 为半径画弧,与21、23、41、43的延长线相交,即得两条大圆弧。分别以1、3为圆心,1 A 为半径画弧,与所画的大圆弧连接,即近似地得到所求的椭圆,如图2-128所示。
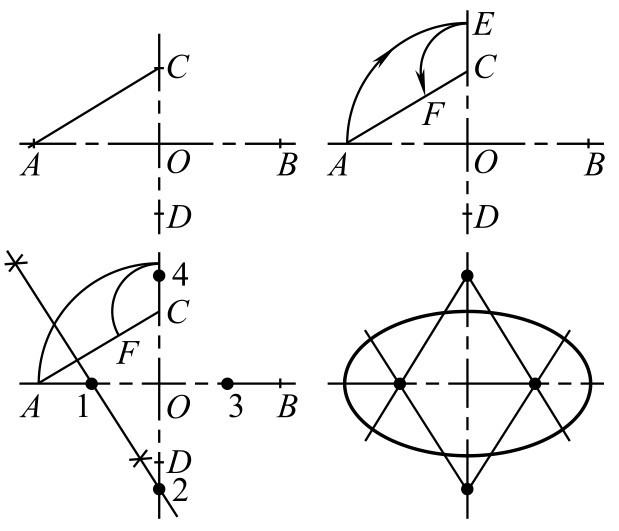
图2-128 四心法画法
已知腰子圆的短轴 a ,长轴 b 。作法如图2-129所示。
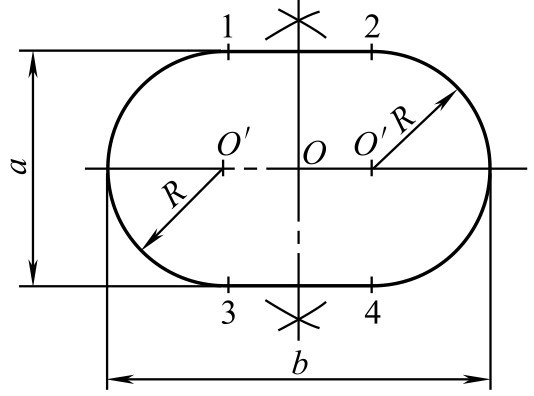
图2-129 腰子圆的画法
①作以 O 点为中心的十字线。
②在长轴的对称中心线上取出两个
O
′点,使
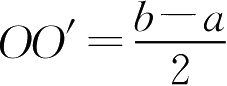 ,
O
′点成为腰子圆的圆心。
,
O
′点成为腰子圆的圆心。
③以
O
′点为圆心,
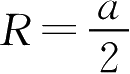 为半径作两个半圆,并画出它们的公切线,得出1、2、3、4这4个切点。
为半径作两个半圆,并画出它们的公切线,得出1、2、3、4这4个切点。
已知大、小圆半径为
R
和
R
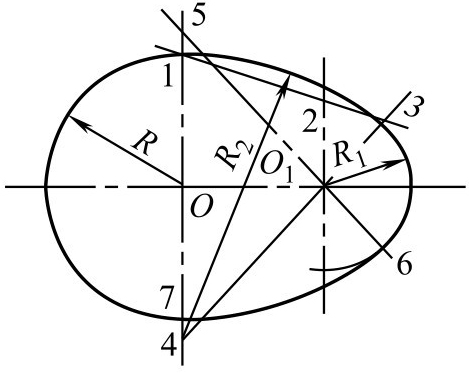
图2-130 大、小圆的圆弧连接作法
①分别以 O 1 和 O 2 为圆心,以 R 和 R 1 为半径,画出大、小两个圆,并与两圆中心线相交于1、2点。
②连接1、2两点,并延长交于 R 1 圆弧上3点,连接3、 O 1 ,并延长交于4点。
③以4为圆心,1、4长为半径,画圆弧交于1、3点。同理,画圆弧交于7、6点。
铆工作业中,对某些巨大的金属结构,如大型储气罐的罐顶,放样时会遇到作特大圆弧的问题,即知罐体的直径(弦长) AB 和罐顶拱高(弧弦距) h 。两种大圆弧的近似作法介绍如下。
作法1 (如图2-131所示)
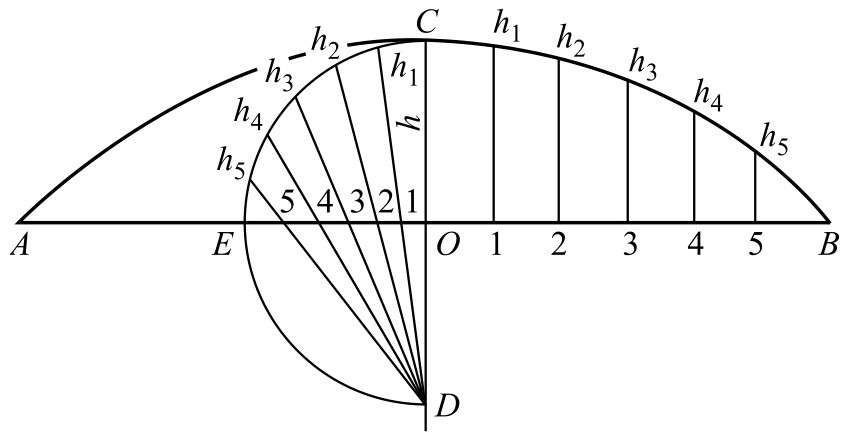
图2-131 特大圆弧的近似作法(1)
①作 AB 的垂直平分线 OC ,取 OC = h 。
②以 O 为圆心, OC 长为半径画半圆 CED 。
③分 CE 弧为6等分,过 D 点作各等分点的连线,交 OE 线于1、2、3、4、5点。
④分 AB 弦为与半圆的同数(12)等分,并过等分点作垂线,在各垂线上取对应等于 h 5 —5、 h 4 —4、 h 3 —3、 h 2 —2、 h 1 —1的距离,得到各点。
⑤用光滑的曲线连接各点,即得精度不高的大圆弧。
作法2 (如图2-132所示)
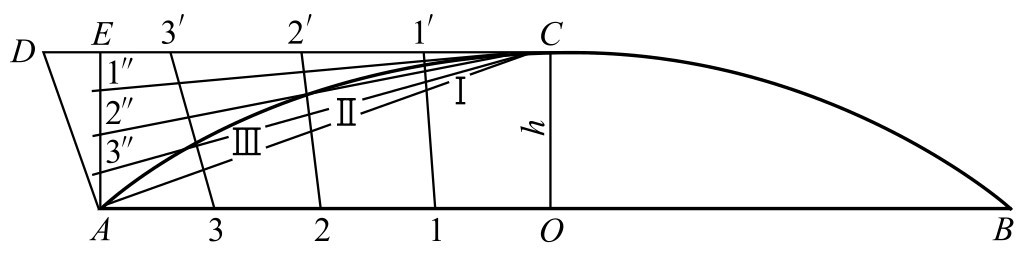
图2-132 特大圆弧的近似作法2
①作弦长 AB 的垂直平分线,并取 OC 等于弧弦距 h 。
②连接 AC 作 CD 平行于 AB , AD 垂直于 AC , AE 垂直于 AB (即也垂直于 CD )。
③分别将 AO 、 EA 、 DC 4等分,连接1—1′、2—2′、3—3′和 C —1″、 C —2″、 C —3″。
④上述两组线的对应交点Ⅰ、Ⅱ、Ⅲ,与 A 、 C 点,用光滑的曲线连接,即得到较准确的大圆弧。
已知基圆 D 作圆的渐开线。
①将基圆 D 分成任意等分,并将基圆的展开长度π D 也分成相同的等分(图中为12等分)。
②在圆周上的各分点处,按同一方向作圆的切线。
③在切线上依次截取π D 的1/12、2/12、3/12、…得一系列的点,用曲线板光滑连接诸点,即为所求的渐开线,如图2-133所示。
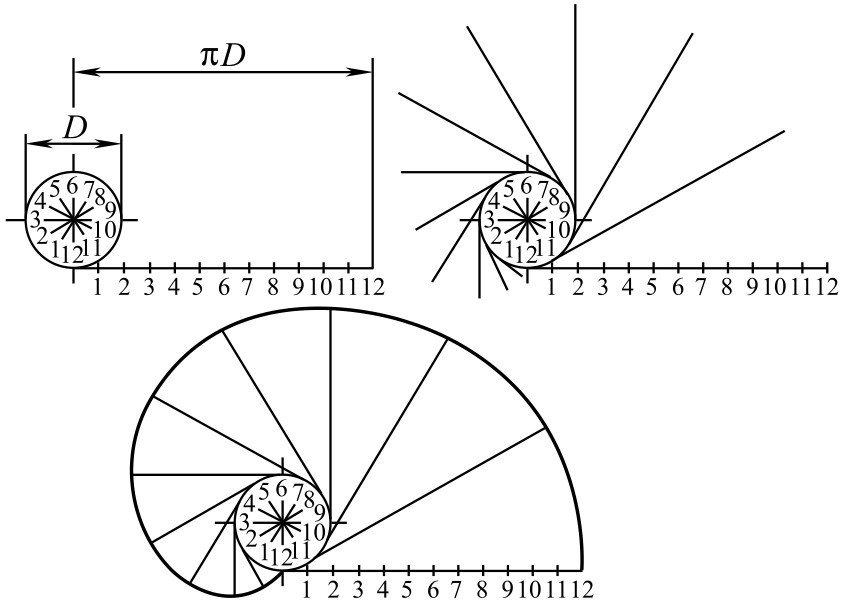
图2-133 渐开线画法
平面图形都是由各种线段(直线与曲线)连接而成的,线段的长短、形状和位置是由图形的尺寸所决定。因此,要迅速、准确地绘制平面图形,必须对图形的尺寸和线段进行分析。
平面图形中所注的尺寸,按其作用可分为以下两大类。
①定形尺寸 用以确定平面图形各组成部分形状和大小的尺寸称为定形尺寸,如圆和圆弧的直径(或半径)、线段的长度和角度的大小等。如图2-134中的 ф 16、 ф 10、 R 8、 R 40、 R 48、 R 8等尺寸。
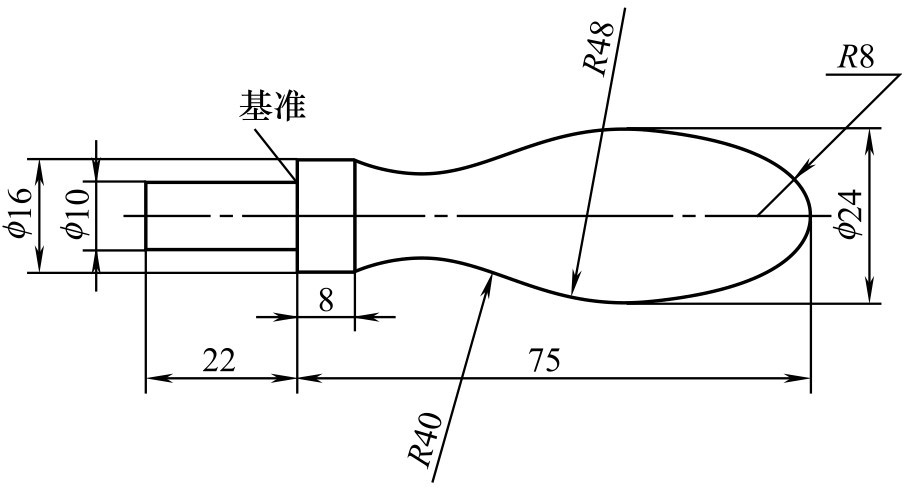
图2-134 手柄各部尺寸
②定位尺寸 用以确定平面图形中各组成部分之间相对位置的尺寸称为定位尺寸。如图2-134中,75是 R 8圆弧的定位尺寸, ф 24是 R 48圆弧的定位尺寸。
标注尺寸首先要确定尺寸基准,所谓尺寸基准就是标注尺寸的起点。对平面图形来说,应有水平和垂直两个方向的尺寸基准,通常取图形的边界线、轴线、对称线或中心线等作为尺寸基准。
按其作用可分为3类:已知线段,中间线段,连接线段。
①已知线段 凡定形、定位尺寸齐全,可以直接画出的线段,称为已知线段。如图2-134中,手柄左端的两个长方形,右端的圆弧 R 8,都是已知线段。
②中间线段 只有定形尺寸而定位尺寸不全的线段称为中间线段。作图时,须部分依赖于其它线段才能画出,如图2-134中的 R 48为中间线段。
③连接线段 只有定形尺寸而没有定位尺寸的线段称为连接线段,如图2-134中的 R 40为连接线段。
①分析图形,画出基准线。
②画已知线段。
③画中间线段。
④画连接线段。
①画中心线和已知线段的轮廓,以及相距为24的两根范围线,如图2-135(a)所示。
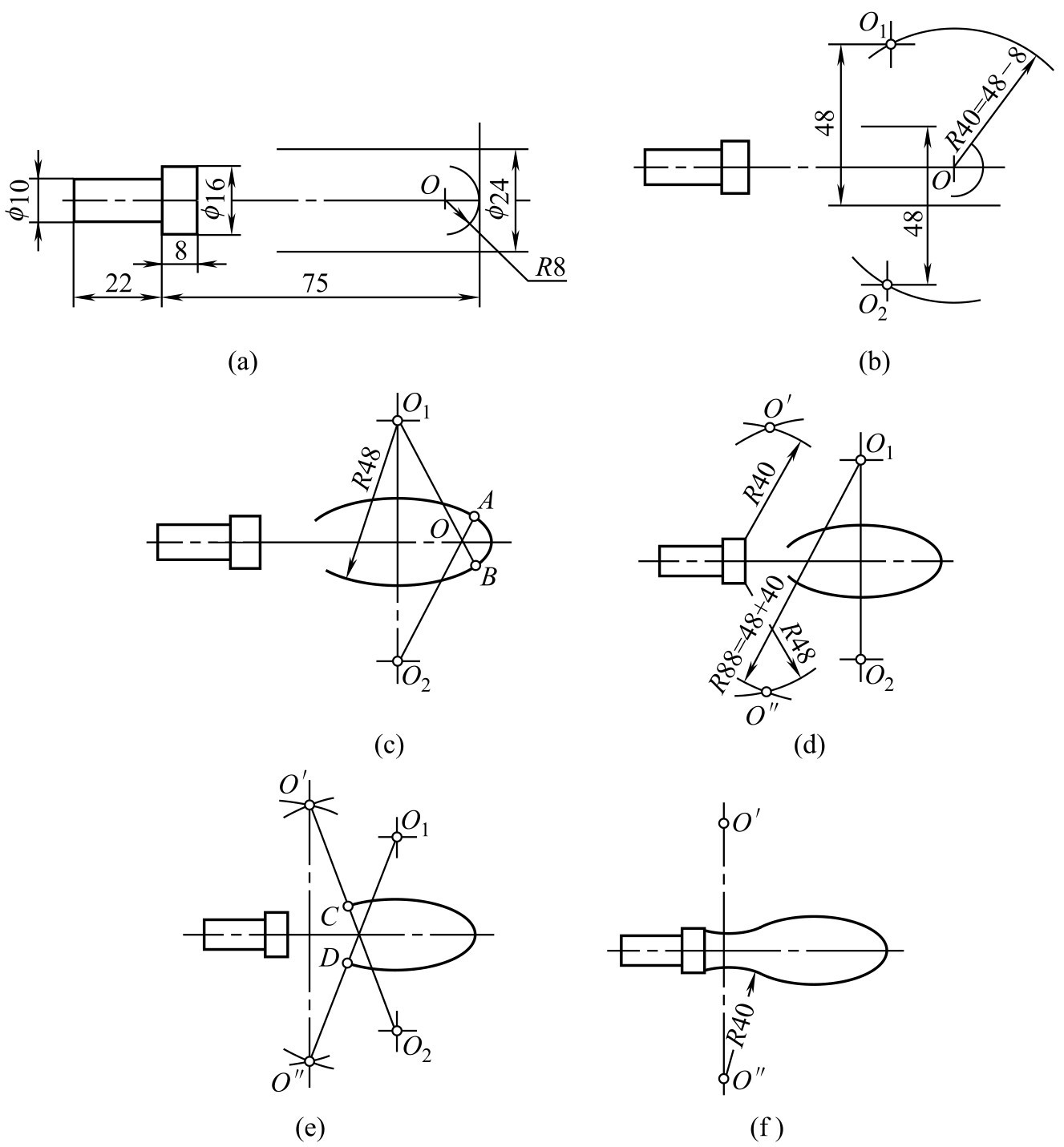
图2-135 手柄画图步骤
②确定连接圆弧 R 48的中心 O 1 及 O 2 ,如图2-135(b)所示。
③确定连接圆弧 R 48和已知圆弧 R 8的切点 A 、 B ,并以48为半径画圆弧,如图2-135(c)所示。
④确定连接圆弧 R 40的圆心 O ′和 O ″,如图2-135(d)所示。
⑤确定 R 40和 R 48的切点 C 、 D ,如图2-135(e)所示。
⑥以 O ′和 O ″为圆心,以40为半径画圆弧,即完成作图,如图2-135(f)所示。
以目测估计图形与实物的比例,按一定的画法要求徒手(或部分使用绘图仪器)绘制的图,称为草图。在生产实践中,经常需要借助草图来记录或表达技术思想。因此,绘制草图是工程技术人员必备的一种基本技能。
徒手画草图一般用HB或B铅笔。为了提高徒手绘图的速度和技巧,必须掌握徒手绘制各种线条的基本手法。
①直线的画法 画直线时,可先标出直线的两端点,手腕靠着纸面,眼睛注视线段终点,匀速运笔一气完成。画水平线时,为了便于运笔,可将图纸斜放,如图2-136(a)所示;画垂直线应自上而下运笔,如图2-136(b)所示;画斜线时,可以调整图纸位置,使其便于画线,如图2-136(c)所示。
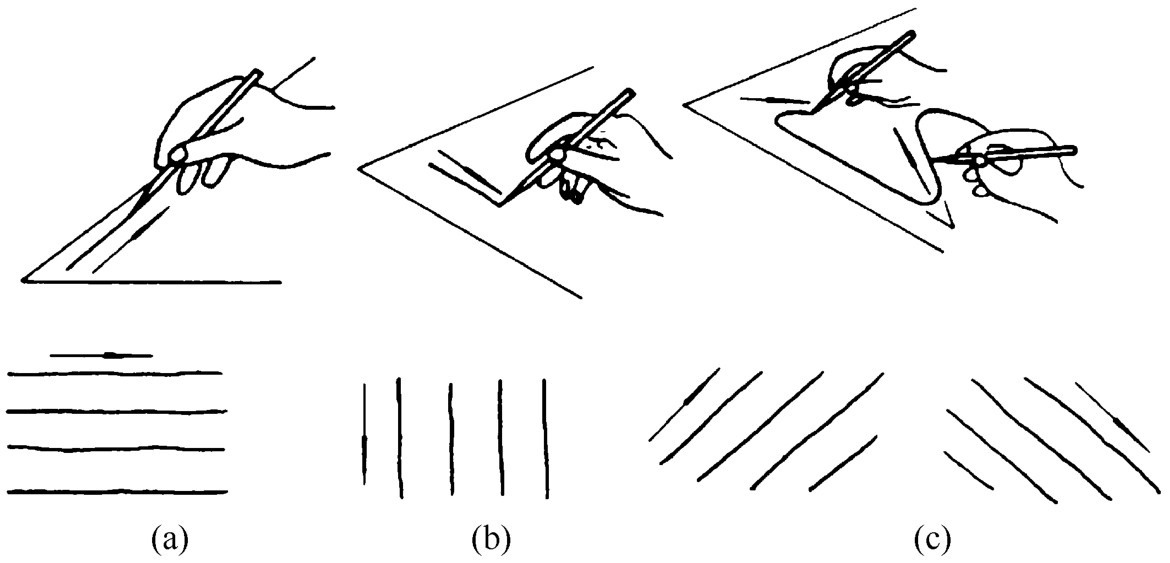
图2-136 直线的徒手画法
②常用角度的画法 画30°、45°、60°等常用角度时,可根据两直角边的比例关系,在两直角边上定出两端点后,徒手连成直线,如图2-137所示。
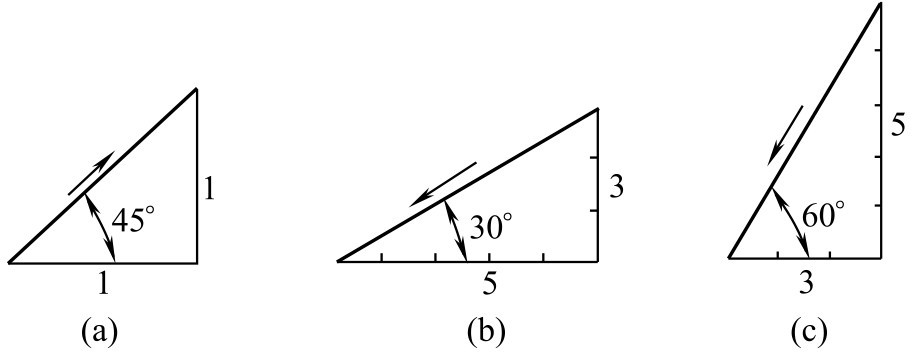
图2-137 角度线的徒手画法
③圆的画法 画直径较小的圆时,先在中心线上按半径大小目测定出四点,然后徒手将这4点连接成圆,如图2-138(a)所示;画较大圆时,可通过圆心加画两条45°的斜线,按半径目测定出八点,然后连接成圆,如图2-138(b)所示。
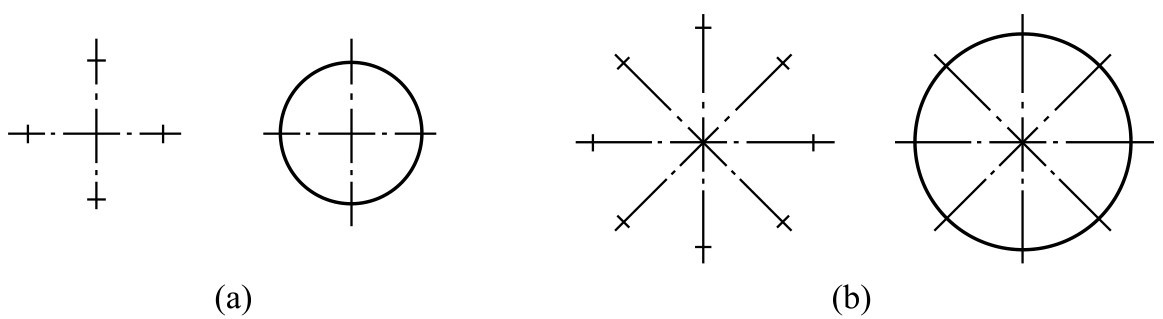
图2-138 圆的徒手画法
④圆角及圆弧连接的画法 画圆角及圆弧连接时,根据圆角半径大小,在分角线上定出圆心位置,从圆心向分角两边引垂线,定出圆弧的两连接点,并在分角线上定出圆弧上的点,然后过这3点作圆弧,如图2-139(a)所示;也可以利用圆弧与正方形相切的特点画出圆角或圆弧,如图2-139(b)所示。
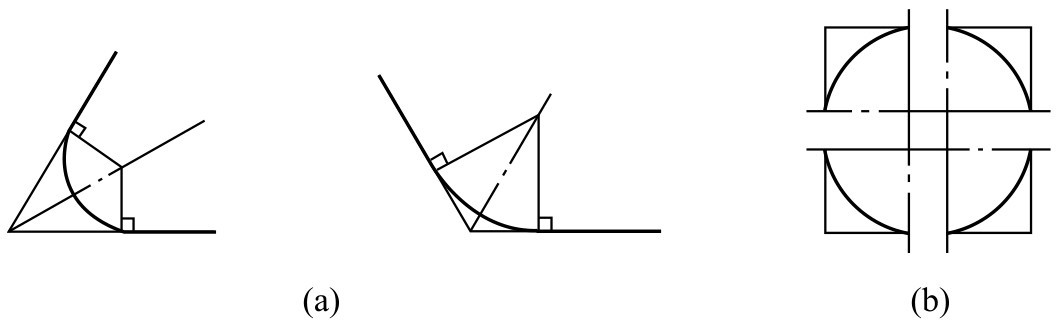
图2-139 圆角、圆弧连接的徒手画法
⑤椭圆的画法 画椭圆时,先画椭圆长、短轴,定出长、短轴顶点,过4个顶点画矩形,然后作椭圆与矩形相切,如图2-140(a)所示;或者利用其与菱形相切的特点画椭圆,如图2-140(b)所示。

图2-140 椭圆的徒手画法
其步骤与仪器绘图的步骤相同。草图图形的大小是根据目测估计画出的,目测尺寸比例要准确。初学徒手绘图,可在方格纸上进行,如图2-141所示。
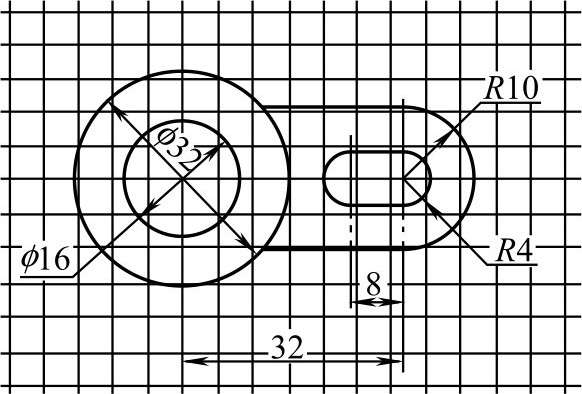
图2-141 徒手画平面图形示例
草图不是潦草的图,虽为徒手绘制,但不能马虎。要求原理正确,内容完整,线型分明,字体工整,图面整洁。