




药物的化学稳定性与药物体系的分解速率密切相关,而药物在体内的代谢过程与药物的生物转化速率有关。某些药物在体外并无药理活性,需进入体内,分解成活性成分后,方能发挥药效。这些基本上都属于化学反应,其反应速率与发生药效的快慢和作用时间的长短均密切相关。
各种化学反应的速率各不相同,有些化学反应速率很快,瞬间就能完成,如燃烧、爆炸、溶液中的一些离子反应;有些化学反应速率很慢,如在常温常压下氢气和氧气化合生成水的反应,慢得几乎不能察觉。
为了比较反应的快慢,必须明确反应速率的概念,规定它的单位。化学反应速率( v )通常用单位时间内反应物或生成物浓度的变化来表示。时间( t )单位用分(min)或秒(s),浓度 c 的单位为摩·升 -1 (mol·L -1 )。即

反应速率( v )可选用反应体系中任一物质变化来表示,现举例说明。
【例1-105】 某一定条件下,在恒容容器中氮与氢合成氨,各物质浓度变化如下:
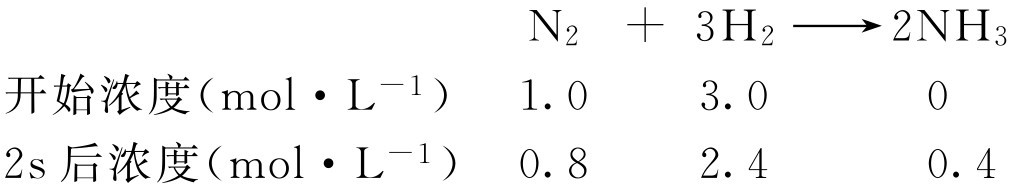
计算反应速率 υ 。
解:
用N
2
的浓度变化表示:
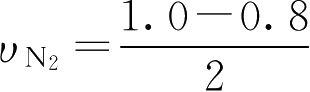 =0.1(mol·L
-1
·s
-1
)
=0.1(mol·L
-1
·s
-1
)
用H
2
的浓度变化表示:
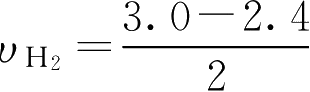 0.3(mol·L
-1
·s
-1
)
0.3(mol·L
-1
·s
-1
)
用NH
3
的浓度变化表示:
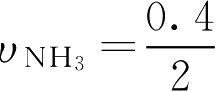 =0.2(mol·L
-1
·s
-1
)
=0.2(mol·L
-1
·s
-1
)
(一)基元反应和非基元反应
基元反应是指一步完成的化学反应,它也是非基元反应所经历的各基本步骤,鲜明地反映出反应速率的规律性。以下反应属于基元反应:
CO+NO 2 →CO 2 +NO
2NO 2 →2NO+O 2
SO 2 Cl 2 →SO 2 +Cl 2
非基元反应是指两步或两步以上完成的反应,又称复杂反应。多数反应属于复杂反应。例如在酸性环境中,过氧化氢溶液氧化Br - 的反应方程式为:
H 2 O 2 +2H + +2Br - →Br 2 +2H 2 O
根据实验测定,该反应是以下四步进行的非基元反应,即:

其中每一步均为一个基元反应。
(二)质量作用定律
质量作用定律是指在恒定温度下,基元反应的反应速率与各反应物浓度幂的乘积成正比。浓度的幂次在数值上等于基元反应中各反应物化学式前的系数。例如:
NO 2 +CO→CO 2 +NO
此反应的质量作用定律表示为:
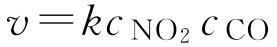
对于任一基元反应:
a A+ b B→ c C+ d D
质量作用定律的数学表达式为:
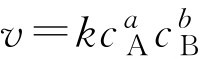
上式称为速率方程。式中, v 为反应的瞬时速率; c A 、 c B 分别表示A、B反应物的瞬时浓度; a 、 b 表示反应方程式中A、B物质化学式前面的系数; k 称为速率常数,其物理意义是,在一定温度下,反应物为单位浓度时的反应速率。在相同温度下,当两个反应的反应物都为单位浓度时,速率常数较大,其反应速率也较快。 k 是一个特征常数,其数值大小与反应物的本性有关。在相同条件下,不同的化学反应其 k 值往往不同。 k 不受浓度的影响,但与反应温度和催化剂等有关。
对于非基元反应,不能应用质量作用定律,如非那西汀的生产过程中有一个乙酰化反应:

其速率方程为
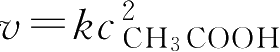 ,它表明乙氧基苯胺浓度并不影响反应速率,而醋酸浓度却能显著影响反应速率。
,它表明乙氧基苯胺浓度并不影响反应速率,而醋酸浓度却能显著影响反应速率。
【例1-106】 340K时,N 2 O 5 浓度为0.160mol·L -1 ,其分解速率为0.056mol·L -1 ·min -1 ,计算该反应的速率常数及N 2 O 5 浓度为0.100mol·L -1 时的反应速率。
解: (1)求 k 2N 2 O 5 (g)→4NO 2 (g)+O 2 (g)
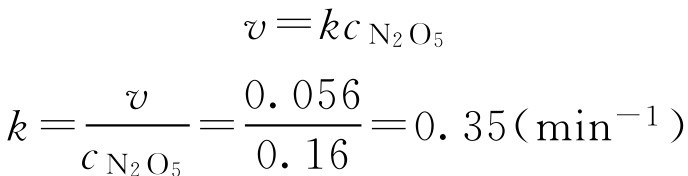
(2)求N 2 O 5 浓度为0.100mol·L -1 时的反应速率
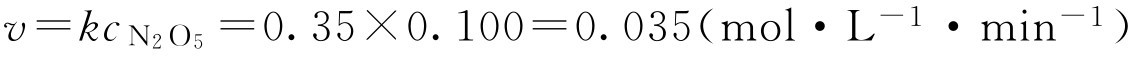
(三)反应级数
速率方程
v
=
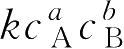 中,反应物浓度的指数
a
、
b
称为级数,所有浓度项的指数之和称为反应级数。例如2NO+O
2
→2NO
2
v
=
中,反应物浓度的指数
a
、
b
称为级数,所有浓度项的指数之和称为反应级数。例如2NO+O
2
→2NO
2
v
=
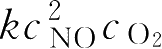 该反应对NO是二级,对O
2
是一级,而整个反应称为三级反应。因此,整个反应的速率与反应物浓度的一次方成正比者称为一级反应,与反应物浓度的二次方成正比者称为二级反应,与反应物浓度无关者称为零级反应,与反应物浓度的分数次方成正比者称为分数级反应。对反应中某些物质来说,可以是负级数,如2O
3
→3O
2
,该反应中,对O
3
为一级,对O
2
为负一级。负级数表示物质能抑制反应。
该反应对NO是二级,对O
2
是一级,而整个反应称为三级反应。因此,整个反应的速率与反应物浓度的一次方成正比者称为一级反应,与反应物浓度的二次方成正比者称为二级反应,与反应物浓度无关者称为零级反应,与反应物浓度的分数次方成正比者称为分数级反应。对反应中某些物质来说,可以是负级数,如2O
3
→3O
2
,该反应中,对O
3
为一级,对O
2
为负一级。负级数表示物质能抑制反应。
酯类药物的水解称准一级或伪一级反应,该反应大多数需H
+
或OH
-
催化,才能使反应进行完全。但如
 或
或
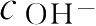 ≫
c
酯
,或用缓冲液保持
≫
c
酯
,或用缓冲液保持
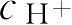 或
或
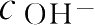 几乎不变,则
v
=
kc
酯
,故为伪一级反应。
几乎不变,则
v
=
kc
酯
,故为伪一级反应。
一个化学反应过程,究竟是属于一级、二级、三级,不能由化学反应式判断。在实践中,化学反应级数都是通过实验确定的。所以确定反应服从哪级反应便可得到反应速率与反应物浓度的关系。
在不同级数的反应中,速率常数 k 可由下式求得:

式中, a + b + c …= n , n 为反应级数。 k 的量纲是(NL -3 ) 1- n T -1 ,其中N、L、T分别是物质的量、长度、时间的量纲符号,L -3 表示体积,因此当浓度用mol·L -1 、时间用s表示时, k 的单位是(mol·L -1 ) 1- n ·s -1 。
【例1-107】 在稀水溶液中,过氧化氢和溴化氢的反应为:
H
2
O
2
(aq)+2H
+
(aq)+2Br
-
(aq)
 2H
2
O(l)+Br
2
(aq)
2H
2
O(l)+Br
2
(aq)
对它进行反应速率测定,实验数据如下:

求:(1)写出该反应的速度方程。
(2)反应级数是多少?
(3)计算反应速率常数。
解: (1)设该反应的速度方程为:
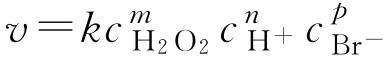
根据上式和实验数据,得
v 1 =1= k (0.1) m (0.1) n (0.1) p
v 2 =0.1= k (0.01) m (0.1) n (0.1) p
v 3 =0.1= k (0.1) m (0.01) n (0.1) p
v 4 =0.1= k (0.1) m (0.1) n (0.01) p
由 v 1 / v 2 得 m =1
由 v 1 / v 3 得 n =1
由 v 1 / v 4 得 p =1

(2)反应级数为1+1+1=3,是三级反应。
(3)将数据代入速度方程,得 k =1000(L 2 ·s -1 ·mol -2 )。
(四)一级化学反应的动力学公式
用数学式来表达化学反应中物质的生成或消失的速度,就是化学动力学。
以反应物浓度的变化表示化学反应速度时:
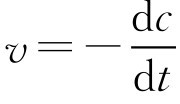
在一级反应中:
v
=
kc
则-
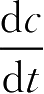 =
kc
=
kc
以上微分式中
c
为反应物在瞬间
t
的浓度。对此式积分,以
c
0
表示反应开始时(
t
=0)的反应物的浓度,则
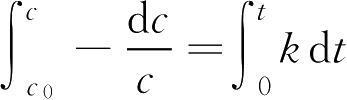
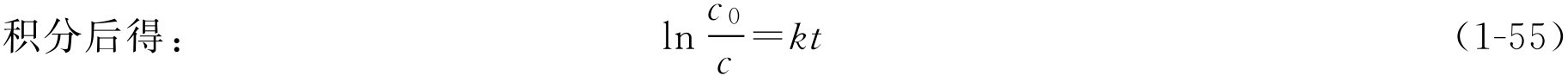
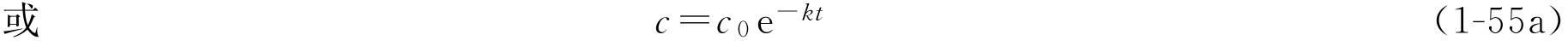
转换为常数对数,则式(1-55a)可写成:

由式(1-55),只要知道一个一级反应的速率常数 k 和反应物起始浓度 c 0 ,则可求得经过任意时间 t 后反应物的浓度。
将式(1-55)移项变换可得

由式(1-57),只要知道反应物起始浓度,再测定经过 t 时间后反应物的浓度 c ,即可确定该反应的反应速率常数 k 。要说明的是,在实践中单凭起始浓度和某时间 t 的浓度来确定 k 值是不准确的。
由于
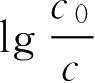 是没有单位的,所以反应速率常数
k
的单位为时间的倒数。即秒
-1
(s
-1
)、分
-1
(min
-1
)、小时
-1
(h
-1
)、天
-1
(d
-1
)、年
-1
等。
是没有单位的,所以反应速率常数
k
的单位为时间的倒数。即秒
-1
(s
-1
)、分
-1
(min
-1
)、小时
-1
(h
-1
)、天
-1
(d
-1
)、年
-1
等。
由式(1-57)可转换为

如 k 已知,由式(1-58)可求得 t 1/2 、 t 9/10 或 t 9.5/10 ,即反应物为初始浓度50%、90%、95%所需的时间。 t 1/2 通常称为半衰期。此时
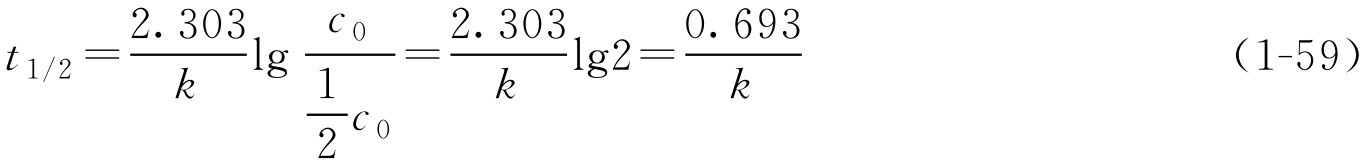
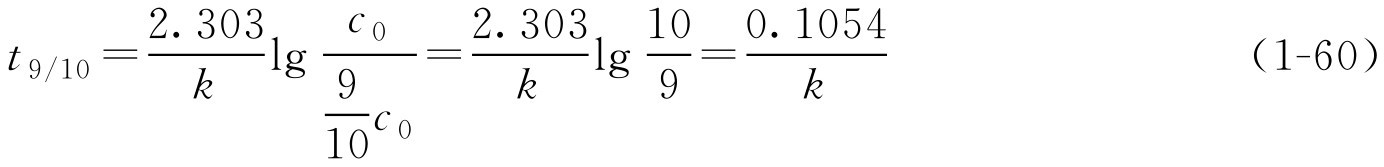
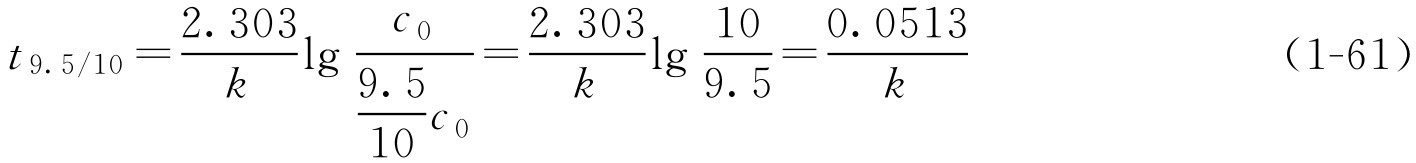
在应用这些公式时应注意以下几点。
① c 和 c 0 的单位要一致。
② t 的单位与 k 的单位相对应。如 t 以秒为单位,则 k 应用s -1 , t 以分为单位, k 用min -1 ,依此类推。
③如用于计算 k ,测定 c 0 和 c 的条件应完全一致,如温度、pH测定方法均应一致。因 k 值与反应物的浓度无关,但随温度、pH等改变而变化。
(五)根据一级动力学公式进行的计算
1.已知初始浓度及某一时间的浓度,计算反应速率常数
【例1-108】 青霉素G钠盐80万单位,在室温(20℃)配制成溶液,于pH=4放置4h后,测定实际含量为63.5万单位,计算青霉素钠盐在该条件下的分解速率常数。
解:已知 c 0 =80 c =63.5 t =4h
由
k
=
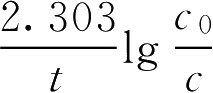 ,得
k
=
,得
k
=
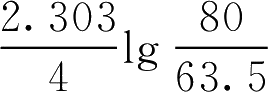 =0.05776(h
-1
)
=0.05776(h
-1
)
即在pH=4、温度20℃时,青霉素钠盐的分解速率常数为0.05776h -1 。
【例1-109】 将阿司匹林溶于pH=4.0的缓冲溶液中使成3g·L -1 ,在17.2℃放置7天后,测得质量浓度为1.56g·L -1 ,计算阿司匹林的水解速率常数。
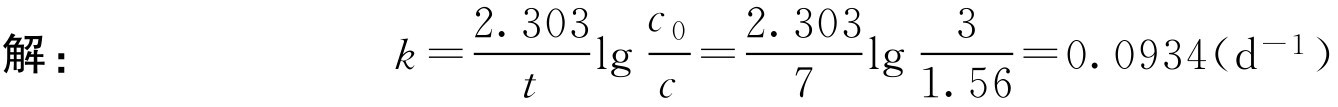
即在pH=4、温度17.2℃时,阿司匹林的水解速率常数为0.0934d -1 。
2.已知反应速率常数及初始浓度,计算某一时间的浓度
【例1-110】 已知青霉素钠盐在pH=7时分解反应速率常数为0.07629d -1 ,问80万单位青霉素G钠盐在pH=7溶液中,放置12h后的含量是多少?
解:
已知
k
=0.07629d
-1
,放置时间
t
=12h,需先将时间换算为天。即
t
=
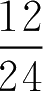 =0.5(d)
=0.5(d)
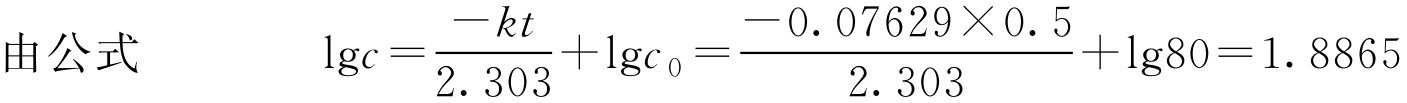
c =lg -1 1.8865=77(万单位)
即放置12h后的含量为77万单位。
【例1-111】 盐酸普鲁卡因注射液在pH=5时的水解速率常数为3.76×10 -5 d -1 ,在此条件下,20g·L -1 盐酸普鲁卡因,放置一年后的质量浓度( ρ B )是多少?五年后的质量浓度( ρ B )又是多少?

已知 k =3.76×10 -5 , t =1年=365d
c 0 =20g·L -1 代入上式得
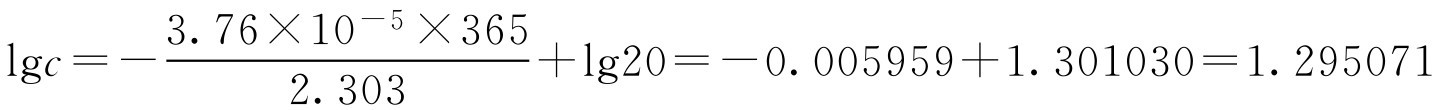
c =lg -1 1.295071=19.7(g·L -1 )
(2)当 t =5年时
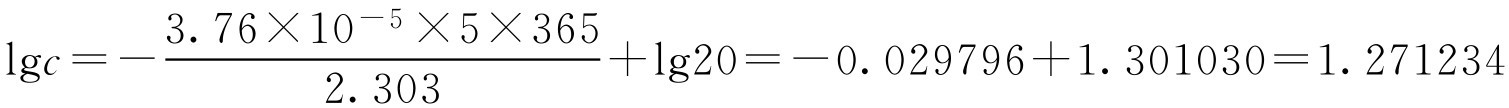
c =lg -1 1.271234=18.7(g·L -1 )
即在pH=5时20g·L -1 盐酸普鲁卡因放置一年后的质量浓度为19.7g·L -1 ,五年后的质量浓度为18.7g·L -1 。
3.已知初始浓度及某一时间的质量浓度,计算达到某一较低质量浓度所需的时间
【例1-112】 5g·L -1 氯霉素滴眼液,在20℃储藏133d后,实际测定损失效价10.72%,已知氯霉素的水解反应属于一级反应,计算其半衰期及效价为原有浓度90%时的储存时间。
解: (1)求速率常数 k
已知 t =133d, c = c 0 -10.72%× c 0 =5-10.72%×5=4.464(g·L -1 )
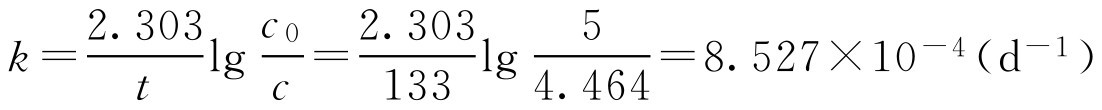
(2)计算 t 1/2
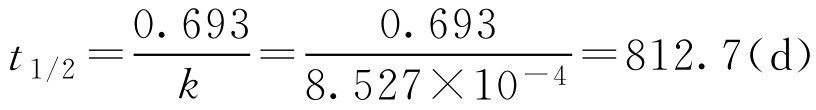
(3)求效价为原有质量浓度90%所需时间
①法。效价为原有质量浓度的90%,即实际质量浓度为90%×5.0=4.5(g·L -1 )
代入公式
t
9/10
=
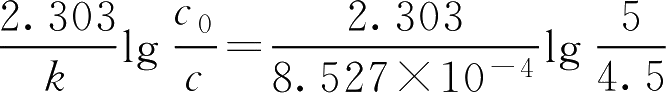 =124(d)
=124(d)
②法。直接按公式
t
9/10
=
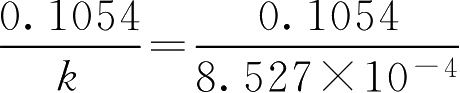 =124(d)
=124(d)
即氯霉素在该滴眼液中的半衰期(20℃时)为812.7d,储存124d后效价为原有浓度的90%。
【例1-113】 有一批维生素B 1 注射液,每支2ml含B 1 100mg,储存2年后,测定实际含量为每支97.5mg。试计算当含量降至每支95.0mg时所需时间(维生素B 1 含量下降的因素是水解,反应速度符合一级化学反应)。
解: 先求反应速率常数 k
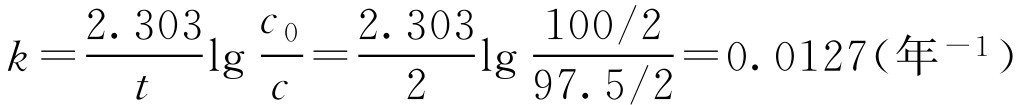
再计算由100mg/2ml降低至95.0mg/2ml所需时间
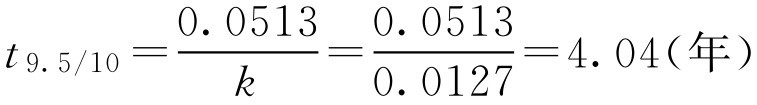
即该批维生素B 1 注射液储存4.04年后含量降至95.0mg/2ml。
4.已知半衰期 t 1/2 或速率常数和初始浓度,计算达到某一较低浓度所需时间
【例1-114】 青霉素G钠盐溶液在pH6.5时的 t 1/2 为236h,如将40万单位的青霉素G钠盐溶解于pH6.5的缓冲液中,当效价降至原来的90%时,需多少时间?
解: 先求得 k
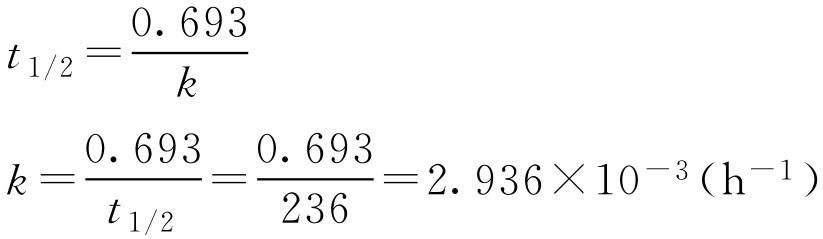
将 k 值代入公式,得
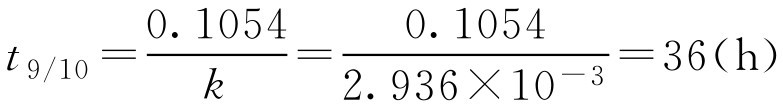
即效价降至原来的90%需36h。
【例1-115】 5g·L -1 氯霉素滴眼液在4℃时水解速率常数为1.13×10 -4 d -1 ,计算其浓度降至4.5g·L -1 时所需时间。
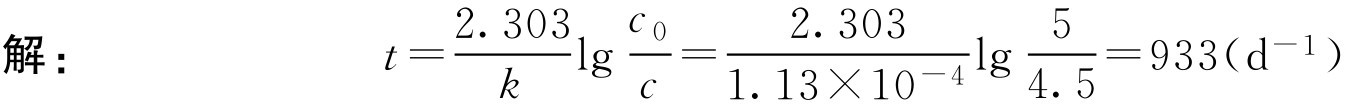
即5g·L -1 氯霉素滴眼液在4℃时储存933d后含量可降至4.5g·L -1 。