前言
P r e f a c e

笔算是当下“最流行”的计算方法。说“流行”也许不太合适，但是多数学校颇为重视教学的形式，几乎每个学校的数学课，都要求学生必须列竖式计算，并将计算的过程详细地写在作业本上，有的学校甚至要求学生用直尺画线。

的确，笔算可以帮助学生清晰地把握、认识计算的“结构”，也可以帮助教师了解孩子们解题的思路。但是，心算的功能是否被过于轻视了呢？

令人心痛的是，如今的课堂上很少涉及心算教学。其实之前心算也曾被大力推广，最近我翻阅小学时代的儿童书时便发现上面非常鼓励孩子们使用“印度式算法”等心算方法来计算“55×55”。

可见，虽然我们曾将这些快速计算的“诀窍”奉若瑰宝，但我们那时并没有真正意识到它的魅力。

我认为现在已经到了复兴心算的时候。我希望通过这本书来帮助人们了解心算的魅力。

为帮助初学者打下良好的数学基础，帮助家长们找到辅导孩子数学的有效方法，帮助日常需要与数字打交道的人更轻松地进行四则运算，我编写了这本《10倍速心算——写给中小学生的56个心算技巧》。

从“机械刻板按部就班的笔算”变为“解读深层原理快速得出答案的心算”。这就是我的目标！

我在辅导班教课的时候，见过许多所谓聪明的和不聪明的孩子。

我发现这些孩子之间最明显，甚至可以说最极端的区别之一便在于他们是否会心算。

在脑中迅速计算，看透数字背后的构成。这种技能即为心算。

只掌握了笔算，而未掌握心算的所谓不聪明的孩子，他们往往只会机械套用老师所教授的步骤，而没有激活自身的数学应用能力。

例如，在计算类似79+146的题目时，只会笔算的孩子是这样解题的：

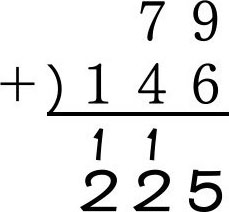
即，将个位数的9和6对齐相加得15，将5写在最右下角的位置，再将1进一位写于左上。然后将十位数的7、4和1相加得12，同样将2写在右下角的位置，将1进一位写于左上。最后将百位数的1和1相加得2，从而得出答案225。

那么，心算该怎么做呢？

比如先关注7和14，计算70+140得210。接下来迅速计算9+6得15，这样二者再相加就得到了225的答案。

更或者将79理解为80-1（看透数字的构成），先计算146+80得226，再将226-1，从而迅速得出225的答案。

换句话说，笔算派会将每一位数都运算三次，记下结果，一步步得出答案。而心算派则会努力看透数字的构成（运用十进制、交换、结合率等），进而迅速地通过多种方法得出答案（如果会用两种以上不同的方法解题，也有利于检查答案）。

读到这里，您是更赞同笔算，还是更赞同心算？

这个问题其实并没有标准答案。

笔算也自有其意义。首先它是一种在任何情况下都通用的标准解法，所以在初级阶段，让孩子进行笔算训练并非坏事。又或者说，如果学生连笔算都无法掌握，也是一件十分令人困扰的事。

但是，如果想在算术上有更大的突破，心算是必不可少的。理由有如下三点：

① 笔算是由教师主导、学生单纯模仿完成的被动式学习。相较之下，心算则需要学生主动探索数字、计算等的关系，在这种不断探索的过程中，我们自然而然可以更深地了解到数字的构成，同时还可以引发学生对数字背后隐藏的更深层次奥秘的兴趣。

② 心算需要在脑中完成一系列数字、图像的操作，因此更有利于学生对整体的把握。这也有利于提高学生对事物的洞察力（这对于今后的学习生活是十分重要的）。

③ 心算的速度是笔算无法匹敌的。学生可以节省大量时间和精力来学习其他复杂的概念，遇到难题时也可以将精力集中于知识难点（而只会笔算的孩子会在计算上浪费大量的时间和精力，无法将思维集中在教师最想教授的知识点上。一半脑力都集中于计算，自然没有更多精力再去思考别的东西）。

以上三点便是我们必须掌握心算的理由。

我认为，学习是一个阶段性的过程。

教师主导教授学习方法、提供学习范本，学生模仿习得，这是学习的第一阶段。这一阶段毫无疑问是非常重要的。

但是若想更好地学习，学生必须自己参与、思考、试错，直到掌握所有知识点。这是第二阶段。

由此可见，笔算在第一阶段的学习中是必不可少的，但当进入第二阶段后，心算能力就显得尤为重要了。

那么，如此重要的心算为什么没有得到重视呢？

答案很简单。

相当一部分家长并不重视孩子的算术学习，这些孩子得不到家长的督促，有些甚至都无法数到数字100。

但这些孩子进入学校后，学校教师就必须努力提高他们的学习能力。这是教师的使命。为了达成这一目标，教师只能在学习的第一个阶段，即在“教授学习方法、提供学习范本，让孩子不断模仿”上耗费大部分的时间。

教师要求学生写下过程，并不断重复模仿，把听到的内容一字不落地记下，检查每一个人的笔记，甚至为了确保全班进度无差别，对于那些已经掌握了笔算，并且希望进一步学习心算的孩子，教师也会要求他们“不可以用心算答题”。

也就是说，虽然笔算和心算各属于第一阶段和第二阶段，用途、功能不同，但学校教育往往必须考虑大多数学生的情况，实行统一教学，这使得教师的指导往往到第一阶段便结束了。

这种情况在辅导班教育中也可以见到。虽然辅导班不会硬性规定学生不能使用心算，但不论他们的水平是否已经超越第一阶段，教师在教应用题时都会要求学生“详细写下算式和过程、做好笔记”，并“画好线段和面积图”。

这种教育方式会对哪些学生产生负面影响呢？

必然是那些知识水平已经超越第一阶段，却被强制永远不能进入第二阶段学习的学生们。

最后，让我们来看一下“计算”的定义：根据已知数目通过数学方法求得未知数。也就是，将用符号连接起来的演算式化为简单的数字。

不过在本书中，“计算”包含的内容则更加广泛，如解联立方程、求平面三角形面积等也在定义之内。

我将通过列举简单的例题，来帮助读者体验数字和演算的规则。而中考题中出现的那些复杂计算题，即“为了计算而计算”的试题则不会在本书中出现。

书中还收编了一些关于计算的拓展性问题，我会在这些高难度的计算题前打上☆号。

那么，就让我们快点进入正题，一起了解计算背后的奥秘，体会心算的魅力吧！