





参见《费曼物理学讲义(第1卷)》第13、14章。
10.1 质量为 m 的物体以速度 v 0 在光滑水平面上滑行,并与弹性系数为 k ,长度为 x 0 的弹簧相撞,如图10-1所示。问:在何处时,物体第一次速度为零?不计弹簧质量。

图10-1
10.2 一弹簧的弹性系数是 k 。在其线性范围内,以一恒定力 F 把弹簧拉到新的平衡位置,请证明:对于新的平衡位置,弹簧的弹性系数不变。
10.3 一中空的球形行星在空间可以自由运行。在其内部,有一质量为 m 的小粒子。问:在行星内部何处小粒子处于平衡位置?
10.4 脱离地球引力场所需速率为(近似地)7.0mi s -1 。某星际探测器刚刚离开地球大气层时的速率为8.0mi s -1 。求当此探测器距离地球10 6 mi时,其相对于地球的速率 v 是多少?
10.5 如果地球所携带的净电荷为1.00 C,那么其电势 φ 将是多少?
10.6 半径为0.50m的球壳上均匀带电,所形成电势为10 6 V。求球壳所带总电量 Q 。
10.7 在没有电火花(或电晕放电)的情况下,在一个大气压强下,干燥的空气所能承受的最大电场强度大约是31 kV cm -1 。计算在空气中,直径为20cm的孤立光滑球体所能达到的最大电势 φ 。
10.8 质量为6.0kg的物体沿 x 轴在无摩擦的轨道上运动。对于下面的每种情况,物体的初始情况皆为 x =0, t =0。
(a)在 x 方向的作用力 F = (3+4 x )N的作用下,物体运行了3.00m。( x 以m为单位。)
1)求物体所达到的速度 v 。
2)求物体在该点的加速度 a 。
3)在该点力对物体所施加的功率 P 。
(b)在 x 方向的作用力 F = (3+4 t )N的作用下,物体运行了3.00s。( t 以s为单位。)
4)求物体所达到的速度 v 。
5)求物体在该点的加速度 a 。
6)在该点力对物体所施加的功率 P 。
习题10.9—10.11中,力 F =1.5 y i +3 x 2 j -0.2( x 2 + y 2 ) k (单位:N)作用于质量为1kg的粒子上。在 t =0时刻,粒子位于 r =2 i +3 j (单位:m)处,以速度 v =2 j + k (单位:m s -1 )移动。
10.9 在 t =0时刻,求:
(a)粒子所受到的力 F ;
(b)粒子的加速度 a ;
(c)粒子的动能 T ;
(d)粒子的动能变化率d T /d t 。
10.10 在 t =0.01时刻,采用近似,求:
(a)粒子的位置 r ;
(b)粒子的速度 v ;
(c)粒子的动能 T 。
10.11 粒子通过无摩擦轨道在力 F 的作用下(同时有约束力)从位置(0,-1,0)移至位置(0,1,0)。在下列情况下,求力 F 所做的功 W 。
(a)轨道是沿 y 轴方向的直轨道。
(b)轨道是位于 yz 平面的圆形轨道。力 F 是保守力吗?
10.12 一辆小车沿倾斜轨道无摩擦地向下滑行。轨道下部是半径为 R 的圆环。为使下车通过圆环而不离开轨道,应从圆环顶部上方多少高度 H 处释放小车?
10.13 如图10-2所示,无摩擦的滑道的最低端是半径为 R 的圆柱面的一部分。这部分圆柱面的两端对中心的张角均为 θ 。滑道的顶点距离其最低点的高度为 H 。质量为 m 的小物体从顶点处由静止开始下滑。

图10-2
(a)求小物体离开轨道后的运动轨迹相对于轨道最低点的最大高度 x 。
(b)求小物体经过轨道最低点时对圆柱面所施加的力 F 。
10.14
质量为
m
(kg)的小滑块通过弹簧和
P
点连接。弹簧松弛时的长度可以忽略。弹簧的弹性系数为
k
(N m
-1
)。弹簧的位置可以调节,但一旦调节好便被固定住,无法再移动。半径为
R
的圆环位于竖直平面内,小滑块可以在圆环的外表面上无摩擦地自由运动,如图10-3所示。
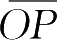 =
d
。如果小滑块从圆环顶部的
A
点由静止开始滑动,当通过圆环底部的
B
点时,小滑块刚刚要脱离圆环,求
d
。
=
d
。如果小滑块从圆环顶部的
A
点由静止开始滑动,当通过圆环底部的
B
点时,小滑块刚刚要脱离圆环,求
d
。

图10-3
10.15 长度为 L ,线密度为 M (kg m -1 )的柔软缆绳悬挂在质量、半径、摩擦均可忽略的滑轮上。起初,缆绳刚好平衡。施加一微小的力,使缆绳偏离平衡,产生一加速度。求当缆绳的端点脱离滑轮时的速率 v 。
10.16 一粒子位于无摩擦、半径为 R 的球面顶部,由静止开始,在重力的作用下沿球面滑行。求粒子离开球面时的位置在起点下方的距离 d 。
10.17 质量为3000lb的小汽车的发动机功率为85hp。以恒定速率30mph行驶所需功率为20hp。假定摩擦力不变,在同样速率下,小汽车能驶上的最大坡度是多少?
10.18 质量为1000kg的汽车以额定功率为120 kW的发动机推动。如果发动机在速率为60km h -1 时达到这样的功率,求汽车的最大加速度 a 。
10.19 1960年,铅球(shot-put)、铁饼(discus)和标枪(javelin)的世界纪录分别为19.30m、59.87m和86.09m。三种投射物的质量分别为7.25kg、2kg和0.8kg。求创造世界纪录的一投各自所做的功 W shot 、 W disc 和 W jav 。(假定运动员都是从离地面1.80m的高度开始,投掷仰角为45°。)
10.20 半径为 R 、质量为 M 的球体,其体内密度均匀。求引力势 φ 和引力场强度 g 关于到球心的距离 r 的函数关系,并画出图像草图。
10.21 如图10-4所示,求距离球表面为 x 的点 P 处的引力加速度 a 。球半径为 R ,密度为 ρ ,内含半径为 R /4的球形空腔。腔心位于 PC 延长线上,距离球心 C 为 R /4。

图10-4
10.22 考虑一厚度为 d 的无限大平板,其材质密度为 ρ 。如图10-5所示,在坐标原点切出一半径为 r ( r < d /2)的球形腔。

图10-5
(a)求位于 y 轴上任意一点 y 上的小质量物体 m 所受的引力 F 。
(b)画出 F 关于 y 的函数图草图。
10.23 一质量为 m 的小物体在引力的作用下绕质量较大的物体 M 运动。运动轨迹是偏心率为 e ,长半轴为 a 的椭圆。(假定 M 保持静止。)计算物体 m 的总能量 E (动能、势能之和)。(注意: E 不依赖于 e 。)
10.24 (a)推导开普勒第三定律。给出物体质量 M ,卫星质量 m ,卫星轨道的长半轴 a ,以及轨道周期 T 之间的关系。
(b)证明:单位质量具有的总能量相同的所有轨道具有相同的周期。(简单起见,假设
m
 M
。)
M
。)
10.25 通常,电容器由两个电量大小一样、符号相反的(金属)体组成。电容 C 定义为(金属)体所带的电量与它们之间的电位差之比

求半径分别为 A 和 B 的一对同心球壳的电容。
10.26 质量为25g的吊架连接在质量忽略不计的弹簧上。弹簧的弹性系数是 k =15.3 N m -1 。一质量为 m =50g的物体从高度 h =9.0cm处落在静止的吊架上,发生非弹性碰撞。求物体能到达的最低高度 H min 。
10.27 水(密度为62.5lb ft -3 )被泵抽进一光滑软管。软管的喷口横截面是5.5in 2 。喷口指向水平面上30°角。水流轨迹的最高点在喷口所在水平面上方16ft处。泵的入口与一水库相连,水库水面在喷口下方8ft处。如果泵和驱动电动机的总效率为60%,问电动机电线对电动机的输入功率 P 是多少(以kW为单位)?
10.28 以大气压(atm)为单位估计月球中心的压强。(1 atm =1.02×10 5 Pa。)使用以下有关月球的数据:
质量:7.0×10 22 kg;
半径:1740km;
表面引力:160cm s -2 ;
平均密度:3.34g cm -3 。
10.29 把一质量为 m 1 的岩石从地球表面移到月球表面最少需要做的功 W min 是多少?(见图10-6。)

图10-6
10.30
一质量为
m
的卫星绕质量为
M
(
M
 m
)的小行星作圆周运动。若小行星的质量突然减小至原来的一半,卫星将要发生什么?描述其新轨道。
m
)的小行星作圆周运动。若小行星的质量突然减小至原来的一半,卫星将要发生什么?描述其新轨道。
10.31 (a)从地球表面附近发射一个星际探测器,为使该探测器在飞离太阳系时相对于太阳有10mi s -1 的剩余速率,发射的最小速率 v min 是多少?
(b)地球在其轨道上的速率是18.5mi s -1 。如果希望探测器在逃脱太阳束缚时以预定方向运动,那么可能的最大发射速度 v max 是多少?
10.32 要把一个太阳探测器送入近日距为0.010AU,且绕太阳运动的周期与地球相同的轨道。问探测器的发射速率 v 0 以及发射角度 α (相对于地球-太阳连线)应是多少?