





参阅《费曼物理学讲义(第1卷)》第11章。
7.1 两物体质量分别为 m 1 和 m 2 ,速度分别为 v 1 和 v 2 ,证明:质心系的运动速度为
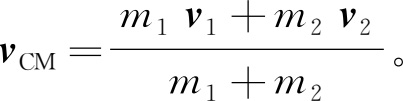
7.2 证明:质量为 m i ,速度为 v i 的 N 个物体,对于某坐标系,总动量为零,则这一坐标系的速度为
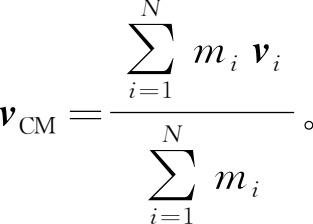
7.3 假定 T 是习题7.1中两物体的总动能, T CM 是它们在质心系中的总动能,证明:
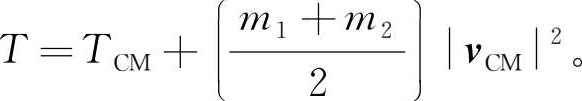
7.4 推广习题7.3的结果至 N 个物体。证明:
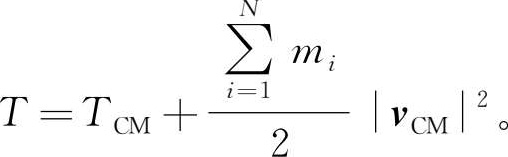
7.5 一个粒子初始位移是 r 0 ,初始速度是 v 0 ,在重力的作用下运动。求 r ( t )。
7.6 已知
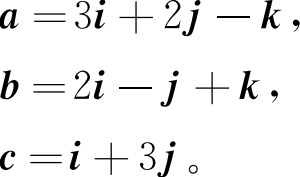
求:
(a) a + b
(b) a - b
(c) a x
(d) a· i
(e) a· b
(f)( a·c ) b -( a·b ) c
7.7 质量为1kg的粒子的运动方式可由下式描述:
r ( t )= t i +( t + t 2 /2) j -(4/π 2 )sin(π t /2) k 。
(a)分别求 t =0和 t =1时刻(单位:秒),粒子的位置,速度 v 和加速度 a 。
(b)求产生这样运动方式所需的力 F ( t )。
(c)求 t =1时刻,粒子的曲率半径 R 。
7.8 以100节速度飞行的飞行员打算向正北飞行。在与机场气象人员的通话中获悉,在他飞行的高度有一股由西向东、速率为25节的风。
(a)他应向什么方向转头?
(b)假定他的目的在100mi远的地方,求飞行时间 T 。(忽略着陆和起飞时间。注意:1节=1.15mi h -1 。)
7.9 一人骑车以10mi h -1 的速率向正北骑行,风由东、北之间一点以6mi h -1 的速率吹来,在骑车人看来,风来自北偏东15°的方向。
(a)求风的真实方向。
(b)如果骑车人返程时以同样速率行驶,在他看来风将是什么方向?
7.10 一人站于宽1.0mi的河的一岸,欲渡到河的正对岸。他有两种方法可供选择:
(a)方向朝上游偏一些以使得速度合方向朝向河正对岸。
(b)方向向正前方,当到达对岸时,由于水流把他冲向了下游,他需沿河岸向上行走,走到正对岸的地方。
如果他游泳速率为2.5mi h -1 ,步行速度为4.0mi h -1 ,水流速度为2.0mi h -1 ,哪种方式更快?快多少?
7.11 一汽艇以相对于河水为 V 的恒定速率在直河道中行驶。河水以恒定速率 R 缓慢行驶。汽艇首先在确定的起点和正上游距离起点为 d 处进行往返行驶。接着在起点和径直横穿河流的方向上距离起点 d 处进行往返行驶。为简单起见,假定汽艇一直在全速行驶,并且在路程终点处转头的时间不计。如果 t V 是沿水流方向作往返行驶所需的时间, t A 是横穿水流方向作往返行驶所需的时间, t L 是汽艇在湖面上行驶2 d 距离所需的时间。
(a)求 t V / t A 。
(b)求 t A / t L 。
7.12 利用矢量求地球上两点[两点的纬度和经度分别为( λ 1 , φ 1 )和( λ 2 , φ 2 )]间的大圆距离(great circle distance) D 。
7.13 求以下情况的月球加速度 a (包括大小和方向)。
(a)新月。
(b)弦月(1/4满月)。
(c)满月。
注意:地球、太阳间距离,地球、月亮间距离分别为:
R E-S =1.50×10 8 km,
R E-M =3.85×10 5 km。
另 M S =3.33×10 5 M E ,其中, M S 和 M E 分别为太阳和地球的质量。
7.14 用两个完全一样的、表面光滑的45°楔形物 M 1 和 M 2 推动表面光滑、质量为 M =384kg的物体,如图7-1所示。两个楔形物都放置在光滑水平面上。其中, M 2 靠在竖直墙面上;一595kg重量的水平力 F 作用在 M 1 上。
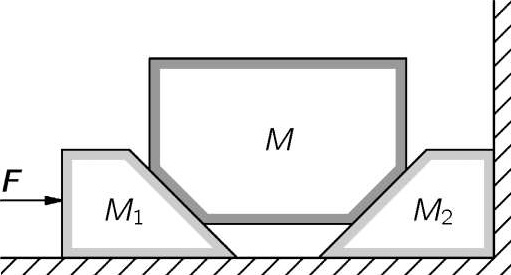
图7-1
(a)求可移动楔形物 M 1 的加速度 a 1 (大小和方向)。
(b)求物体 M 的加速度 a (大小和方向)。
(c)求稳定楔形物 M 2 施加在 M 上的力 F 2 。
忽略摩擦力。
7.15 质量为 m 的物体系于一根任意长的弦的一端,被悬挂在一无摩擦的枢轴上,并使其在水平圆轨道上旋转,旋转平面在枢轴点的下方 H 距离,如图7-2所示。求物体在轨道上的旋转周期 T 。
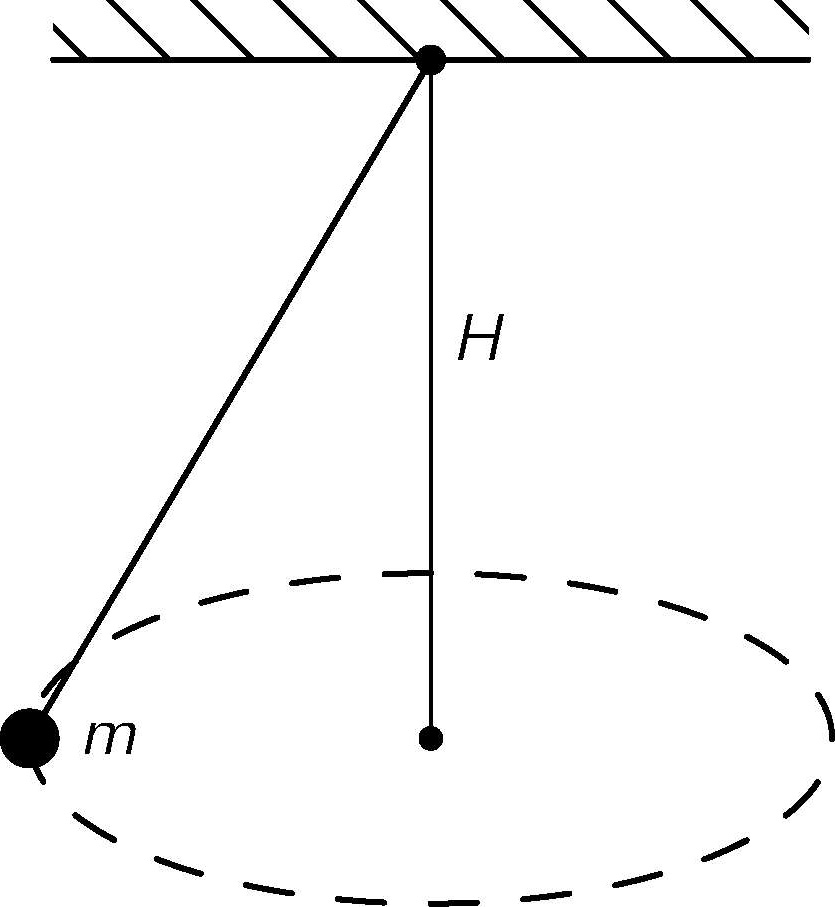
图7-2
7.16 两个黏性小泥球 a 和 b ,质量均为1g,在重力的作用下以-9.8 k m s -2 的加速度运动。给定初始条件: t =0时刻,
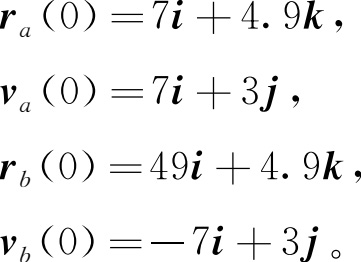
求 t >0的所有时刻的 r a ( t )和 r b ( t )。
7.17 你在一艘以15节的速率向东定向行驶的船上。观测到另一艘船(已知此船在以26节的速率定向行驶)在你正南方6.0mi处;后来发现,此船穿越到你后面,其离你的最近距离为3.0mi。
(a)求另一艘船的行驶方向。
(b)从位于你正南方到离你最近,另一艘船行驶时间 T 是多少?