





从第一个自然哲学家泰勒斯开始,到马其顿王亚历山大大帝征服全希腊为止的二百多年,是希腊科学的古典时代。可以按时期和区域分为三个阶段:第一阶段是爱奥尼亚阶段,第二阶段是南意大利阶段,第三阶段是雅典阶段。公元前5世纪之前,希腊的殖民城邦文化比本土更为发达。首先是爱琴海东岸的爱奥尼亚地区。在那里,从泰勒斯开始直到阿那克萨哥拉,形成了以唯物主义自然哲学为特色的爱奥尼亚学派。几乎与此同时,在西方的意大利南部,从毕达哥拉斯开始直到恩培多克勒,形成了以数的哲学为主要特色的南意大利学派。后来,这两个学派相继随地区的衰落而衰落,雅典开始成了主要的活动舞台。著名哲学家苏格拉底、柏拉图和亚里士多德便活跃在雅典的学术讲坛上。

福尔茨(Philipp von Foltz,1805—1877)的油画《伯里克利的葬礼演说》(1852),画面上,伯里克利正在普尼克山上向雅典公民发表演讲,背景是雅典卫城。
在希腊诸城邦中,雅典本来不是很有名,从公元前594年著名政治家梭伦被推举为执政官后,才逐步变得强大起来。梭伦上任后推行了一系列的政治改革措施,其中包括提高中下等阶级的政治权利、组织最高法庭以扼制执政官的权力等。此外,梭伦还发动了符合下层劳动群众利益的经济改革。另一位政治家克里斯提尼追随梭伦的脚步,进行了更广泛深入的民主体制改革,被称为雅典民主制之父。到了伯里克利时代(公元前461—前429),雅典的民主体制进入了全盛时期。
公元前493年,波斯帝国向地中海东岸扩张,那里的希腊移民受到威胁。身处希腊本土的雅典人对同胞的遭遇极为同情,决心同波斯人开战,以支持爱奥尼亚地区的希腊殖民地。波斯人派出强大的陆军和海军进攻希腊本土,全希腊处在危险之中。雅典人勇敢地担负起领导、指挥反侵略战争的使命。这场战争持续了43年,直到公元前449年才缔结和约休战。在赢得这场艰苦的战争的过程中,雅典人起了重要的作用,同时也确立了自己在希腊世界中的霸主地位。不过,雅典的帝国主义不久即遭到斯巴达人的不满,引起了另一场与斯巴达人的战争,即著名的伯罗奔尼撒战争。这场连绵了27年的希腊内战自公元前431年开始,到公元前404年为止,虽以雅典战败告终,但全希腊都受到了致命的打击。政治动荡加上经济凋敝,使希腊社会元气大伤,最后在政治上屈服于马其顿的统治,结束了古典时代。

雅典卫城。吴国盛摄
西方历史上第一个自然哲学家泰勒斯诞生于地中海东岸爱奥尼亚地区的希腊殖民城邦米利都。他既是第一个哲学家,也是第一个科学家,是西方科学-哲学的开创者。他的学生阿那克西曼德及后者的学生阿那克西米尼也是米利都人,他们形成了西方哲学史上第一个哲学学派——米利都学派。
米利都在今土耳其境内,地处入海口。公元前8世纪至前6世纪,它的海外贸易极为发达,以至希罗多德多次说到“米利都是海上的霸主”。虽然到了泰勒斯生活的年代,其霸主地位已经遭到严重威胁,但它便利的交通条件以及与各国的频繁交往,依然孕育了第一朵希腊文明之花。

泰勒斯雕像
泰勒斯的生卒年月无法准确查考。一是因为年代过于久远,相关历史文献未能保存下来,二是因为那时世界上无统一纪年,参照不同事件的纪年所给出的年代彼此不一致。确定泰勒斯生卒年代最主要的依据是据说他曾经预言过一次日食。运用现代天文学成就可以把该地区历史上所有发生日食的时间推算出来,一共只有三次:一次是公元前610年9月30日,一次是公元前597年7月21日,再一次是公元前584年5月28日。比较多的历史学家倾向于相信最后一次正是泰勒斯预言到的那一次。
即使能确定泰勒斯预言了公元前584年5月28日的日食,又如何知道他的生卒年月呢?对于希腊哲学史上前苏格拉底时期的哲学家来说,这个问题具有某种普遍性。哲学史家发明了“鼎盛年”的概念来解决这一问题,即假定某一哲学家在参与某一重大的历史事件时正处于其最成熟的年龄,而且把这一年龄定为40岁。如果泰勒斯预言日食时正处于鼎盛年,那么他大约生于公元前624年。但也有人转述希腊历史学家的看法,说他生于第35届奥林匹克竞技会那一年(四年一次的奥林匹克竞技会一直被历史学家作为希腊历史纪年的参照系),即公元前640年。他大概高寿,因为有人说他活了90岁。
泰勒斯生于米利都一个名门望族家庭,带有腓尼基人的血统,是当时希腊世界的著名人物,被列为“七贤”之一。七贤中包括雅典的执政官梭伦。泰勒斯也是在担任执政官时被称为贤人的。与其他贤人不同的是,他不仅在政治事务中聪明、能干,而且懂得自然科学,是第一个天文学家、几何学家。在他的墓碑上刻着:“这里长眠的泰勒斯是最聪明的天文学家,米利都和爱奥尼亚的骄傲。”

米利都剧场遗址。吴国盛摄
泰勒斯年轻的时候曾经游历过巴比伦和埃及,从巴比伦人那里学习了先进的天文学理论,从埃及人那里学习了先进的几何学知识。出于航海的需要,米利都人很重视天象观测,而巴比伦的天文学在当时是最发达的。据说泰勒斯写过关于春分、秋分、夏至、冬至的书,观测到太阳在冬至点和夏至点之间运行时速度并不均匀,还发现了小熊星座,方便了导航。这些都可能是他从巴比伦学来的。此外,他之所以能预言日食,也显然是向巴比伦人学习的结果。第二章曾提到,大约在公元前600年巴比伦人已经发现了沙罗周期,即每过223个朔望月发生一次日食的规律。泰勒斯如果知道了这一规律,并且利用巴比伦人的天象记录,是完全可能预言日食的。
泰勒斯本人还亲自观察星象。柏拉图在《泰阿泰德篇》中记述了一段故事,说的是泰勒斯夜里专注于观察天空,不小心掉进了井里。这场景被一位女奴看见了,于是她笑话泰勒斯光热衷于天上发生的事情,却连脚底下的事情都没有看见。
 这个故事具有象征意义。它表明哲学和科学作为一种理论思维在某种意义上是脱离实际的,没有这种对身边俗务的超脱,没有对看似无实际意义的东西的爱好和关注,就没有哲学和理论自然科学。事情发生在西方第一个哲学家和科学家身上,这种象征意义尤为突出。
这个故事具有象征意义。它表明哲学和科学作为一种理论思维在某种意义上是脱离实际的,没有这种对身边俗务的超脱,没有对看似无实际意义的东西的爱好和关注,就没有哲学和理论自然科学。事情发生在西方第一个哲学家和科学家身上,这种象征意义尤为突出。
与此相关的还有另一个故事,是亚里士多德在《政治学》中提到的。泰勒斯一度很贫困,遭到人们的轻视。大家说,哲学有什么用,知识有什么用,到头来还不是囊中羞涩?泰勒斯对此不以为然。有一年冬天,他运用天文学知识预测到来年橄榄将大丰收,于是将手头资金全部投入,租用了当地所有的榨房。由于没有人与他竞争,租金很低。到了收获季节,橄榄果然大丰收,榨房的租金一下子上去了,泰勒斯一举发了大财。他向人们表明,哲学家致富是容易的,只是他们的抱负不在此处而已。

泰勒斯第一个把埃及的测地术引进希腊,并将之发展成为比较一般性的几何学。这方面的具体细节已经无法考证,历史文献只有片段的记述。有的说他成功地在圆内画出了直角三角形后,宰牛庆贺。还有的说他在埃及求学期间运用相似三角形原理求出了金字塔的高度,方法是,当人的影子与人的高度大小一样时,测量金字塔的影子就能得出金字塔的高度。如下几何学定理被认为是泰勒斯提出的:
(1)圆周被直径等分;
(2)等腰三角形的两底角相等;
(3)两直线相交时,对顶角相等;
(4)两三角形中两角及其所夹之边相等,则两三角形全等;
(5)内接半圆的三角形是直角三角形。
这表明,泰勒斯的确为演绎几何学做出了开创性的贡献。
泰勒斯作为第一个自然哲学家留下了一句名言:“万物源于水。”这句话的意义不能仅从字面上理解,因为表面看来,一切都来源于水并不正确,但有意义的是这种说话方式。首先,它是一个普遍性命题,它追究万物的共同本原。这是哲学思维的开始,也是科学地对待自然界的第一个原则。科学从具体、复杂、多样的现象中找出共同的原理,再从原理出发解释、说明、预言更多的现象。其次,它开创了唯物主义传统,它所找到的本原是物质性的本原,而不是任何精神性的东西。这也是自然科学的伟大传统之一,即力求用自然界本身说明自然界,而不求助于非自然界的事物。说万物源于水虽然粗糙朴素,但说话方式是完全新的,对后世科学和哲学的发展有导向性作用。

米利都遗址。吴国盛摄
泰勒斯之所以得出万物源于水的结论,可能是因为他发现一切生命都离不开水,种子只有在潮湿的地方才能生根发芽,而且他一定发现了大地处于海洋的包围之中,而湿气总是充盈在大地的每个角落。基于对水是万物本原的认识,泰勒斯认为,大地浮在水上,是静止的;地震是由水的运动造成的,就像船在水面上随水晃动那样;水蒸发出的湿气滋养着地上的万物,也滋养着天上的日月星辰,甚至整个宇宙。
泰勒斯的学生阿那克西曼德提出宇宙是球状的,星辰镶嵌在圆球上,这是希腊球面天文学的开始。但他还没有地球的概念,他认为大地是柱状的,像鼓一样,有两个彼此相反的表面,人就住在其中一个表面上。阿那克西曼德的学生阿那克西米尼改进了这个宇宙模型,认为宇宙是个半球,像毡帽一样罩在大地上面,大地则像一个盘,浮在气上。阿那克西米尼认为万物都由气组成,气的浓密和稀散造成了不同的物体。在他的著作残篇中有这样的说法:为什么人嘴里可以吐出热气也可以吐出冷气呢?因为闭紧嘴唇压缩气就吐出冷气,放松嘴唇呼出热气。阿那克西米尼的万物由气组成的理论具有现代科学的特征,其呼气实验可以称为第一次真正的科学实验。
爱奥尼亚后来还出现过一个重要的哲学家阿那克萨哥拉。这位出生于米利都附近的希腊殖民城邦的年轻人,因爱奥尼亚被波斯人攻陷而逃往雅典。这次逃亡的结果是把米利都的文化带到了雅典。他继承了米利都学派的唯物主义传统,关注自然哲学问题,提出了独特的物质结构理论——种子论。种子论主张任何感性的物质都不可能互相归结,只能由带有它本身特质的更小的种子来解释;万物的种子在宇宙创生时处于混沌状态,在宇宙巨大的旋涡运动中才开始分离。阿那克萨哥拉认为,太阳、月亮和星辰不过就是火热的石头,它与地上的物体没有什么本质的区别;太阳只比伯罗奔尼撒大一些。阿那克萨哥拉的这些天才的猜想具有灿烂夺目的理性光辉,今天我们听起来虽感幼稚,却很熟悉、亲切。他的思维方式完全是科学的、理性的。在这里,没有神意的影子,有的只是对自然现象冷静的观察和理性的思考。但是,他的这些超群绝伦的思想在雅典被视为异端。他被抓进了监狱,差点被处死,幸亏伯里克利的调解才免于一死,后来被逐出雅典。

毕达哥拉斯雕像
毕达哥拉斯是西方历史上著名的数学家和哲学家,以他的名字命名的毕达哥拉斯定理在西方学童皆知。这个定理在我国被称为勾股定理,它说的是任何一个直角三角形的两直角边的平方和等于其斜边的平方。许多民族都很早就发现了“勾三股四弦五”这一特殊的数学关系,但一般关系的发现和证明是毕达哥拉斯最先做出的。200年后欧几里得的《几何原本》中给出了这一证明。
毕达哥拉斯虽然著名,但他的生平却难以讲清楚。这不仅因为像泰勒斯等早期希腊哲学家一样,由于事久年湮,其历史生平变得模糊,而且因为毕达哥拉斯学派是一个秘密宗教团体,其教义秘不外传。即使在当时,要了解他们的内部情况也是很不容易的。几乎所有的数学和哲学理论都很难指明是毕达哥拉斯本人提出的,还是他的学生门徒提出的。人们只能笼统地以毕达哥拉斯学派概而称之。但称毕达哥拉斯学派也还是过于笼统,因为这个学派从公元前6世纪末到公元3世纪共延续了800多年。因此,我们还需要限定这里所谓毕达哥拉斯学派只指公元前4世纪以前的早期学派,包括那些在希腊宇宙论发展中起过重要影响的毕达哥拉斯的学生们。

中世纪晚期的木刻画,表现毕达哥拉斯学派数的和谐理论。
毕达哥拉斯于公元前570年左右出生在爱奥尼亚地区的萨莫斯,这是希腊人的殖民城邦之一,与米利都隔海相望。毕氏年轻时周游列国,曾向泰勒斯求学。泰勒斯把他介绍给自己的学生阿那克西曼德,并劝他像自己年轻时一样到埃及去学习。毕氏听从了泰勒斯的教导,在埃及住了相当长的时间,并在那里学习了数学和宗教知识。从埃及回来之后,他离开了家乡萨莫斯,移居南意大利的克罗顿,并在那里讲学收徒。他受到了当地人的尊崇,其学派发展成了一个兼科学、宗教和政治三者于一身的庞大组织。
毕达哥拉斯学派的主要贡献在数学方面。希腊时代的数学含义较广,包括算术、几何、天文学和音乐学四大学科。按照毕氏学派的划分,算术研究绝对的不连续量,音乐研究相对的不连续量,几何学研究静止的连续量,天文学研究运动的连续量。在算术中,他们研究了三角形数、四边形数以及多边形数,发现了三角形数和四边形数的求和规律;在几何学中,他们发现并证明了三角形内角之和等于180°,还研究了相似形的性质,发现平面可以用等边三角形、正方形和正六边形填满。
在音乐学研究的基础上,毕达哥拉斯学派提出了“数即万物”的学说。他们发现,决定不同谐音的是某种数量关系,与物质构成无关。传说,毕达哥拉斯有一次路过铁匠铺,听到里面的打铁声时有变化,走过去一看,原来是不同重量的铁发出不同的谐音。回家后,他继续以琴弦做试验,发现了同一琴弦中不同张力与发音音程之间的数字关系。这些研究必定启发他想到导致万物之差异的不是其物质组分,而是其包含的数量关系,故提出了数即万物的数本主义哲学。
说数即万物当然是荒谬的,但若说事物遵循的规律是数学的,则相当正确。近代科学正是在追寻自然界的数学规律中取得长足进步的,可以说,许多次重大的突破都是由于发现了新的数学规律。毕达哥拉斯主义传统确实是自然科学中最富有生命力的思想传统。
毕达哥拉斯学派把数只理解成正整数,他们相信万物的关系都可归结为整数与整数之比。无理数的发现令他们很伤脑筋,因为无理数不能归结为整数与整数之比。据说有一次,毕达哥拉斯学派的成员在海上游玩,该派成员希帕苏斯提出
 不能表示成任何整数之比,其他成员认为他亵渎了老师的学说,竟将他扔入海中。后来,毕氏学派确实认识到
不能表示成任何整数之比,其他成员认为他亵渎了老师的学说,竟将他扔入海中。后来,毕氏学派确实认识到
 是一个无理数,并且给出了证明。证明用的是归谬法。设
是一个无理数,并且给出了证明。证明用的是归谬法。设
 等于
a
∶
b
,其中
a
和
b
是不可通约的整数,可以得出
a
2
=2
b
2
,由于
a
2
是偶数,
a
必为偶数,因为任一奇数的平方必为奇数;
a
和
b
既不可通约,
a
又是偶数,
b
就必然是奇数。又,
a
既是偶数就可令
a
=2
c
,于是
a
2
=4
c
2
=2
b
2
,
b
2
=2
c
2
,这样
b
2
就是一个偶数,同理
b
也是一个偶数。
b
既是一个奇数又是一个偶数,这是矛盾的,所以一开始的假设不能成立,即
等于
a
∶
b
,其中
a
和
b
是不可通约的整数,可以得出
a
2
=2
b
2
,由于
a
2
是偶数,
a
必为偶数,因为任一奇数的平方必为奇数;
a
和
b
既不可通约,
a
又是偶数,
b
就必然是奇数。又,
a
既是偶数就可令
a
=2
c
,于是
a
2
=4
c
2
=2
b
2
,
b
2
=2
c
2
,这样
b
2
就是一个偶数,同理
b
也是一个偶数。
b
既是一个奇数又是一个偶数,这是矛盾的,所以一开始的假设不能成立,即
 不能表示成两个不可通约的整数之比。
不能表示成两个不可通约的整数之比。
在天文学领域,毕氏学派奠定了希腊数理天文学的基础。首先,毕达哥拉斯第一次提出了作为一个圆球的地球概念。人们从前只有大地的概念,地球的概念是从他开始才有的。这个概念在今天受过科学教育的人看来似乎没有什么了不起,但2500年前认识到这一点却非常了不起。因为即使是今天,也不是所有的人都能认识到这一点。许多未受过西方科学教育的人就不相信大地是一个球形,他们说,若地球是一个圆球,与我们相对那面的人岂不是终日倒悬,随时要掉下去?从直观上看,人们大多会得出天圆地方、天盖地承的结论;从直观上看,天高地低,天上地下,天地判然有别。地球概念的提出,打破了这种天地有别的观念,使地球成为天体之一,具有革命性意义。近代的哥白尼革命某种意义上也只是毕达哥拉斯思想的延续。

萨莫斯港口的毕达哥拉斯纪念铜像。吴国盛摄
其次,毕达哥拉斯进一步提出整个宇宙也是一个球体。它由一系列半径越来越小的同心球组成,每个球都是一个行星的运行轨道,行星被镶嵌在自己的天球上运动。毕氏学派认为,位于宇宙中心的是“中心火”,所有的天体都绕中心火转动。天球只能有10个,因为10是最完美的数字。当时已经知道的天体有地球、月亮、太阳、金星、水星、火星、木星、土星共8个,加上恒星天球,一共只有9个天球,不符合毕氏学派对10这一完美数字的追求。于是,他们又假想出了一个天体叫“对地”,意思是与地球相对。我们在天空中看不见“对地”,因为它总处在中心火的那一边,与地球相对。我们人类居住在地球上背着中心火的一面,因此,既看不到中心火,也看不到“对地”。毕达哥拉斯学派的菲罗劳斯(生活于公元前5世纪的后半叶)留下了毕氏学派最早的残篇,在其中,他给出了一幅宇宙结构图,天体由里到外排列如下:中心火、对地、地球、月亮、太阳、金星、水星、火星、木星、土星、恒星天。
毕达哥拉斯学派既提出了地球概念,也提出了天球概念,这种地球-天球的两球宇宙论模式为希腊天文学奠定了基础。在天球转动的基础上,希腊天文学家运用几何学方法,构造与观测相符合的宇宙模型;在宇宙模型基础上,又进一步促进观测的发展,使希腊数理天文学达到了世界古代科学的顶峰。
继毕达哥拉斯学派之后,公元前5世纪左右,在南意大利的爱利亚出现了一个新的哲学流派,史称爱利亚学派。他们的领袖是巴门尼德,重要的成员包括芝诺。这派哲学主张存在是“一”,而“杂多”的现象界是不真实的。他们主张世界本质上是静止的,运动只是假象。他们在科学史上本没有特别重要的位置,但是,由于芝诺提出过两组著名的关于运动是假象的论证,因而为科学史家所重视。这个论证虽说看起来很荒谬,但由于它触及科学概念中一些根本性问题,令数学家们为此苦恼了几千年。
芝诺关于运动的悖论一共有四个。第一个悖论叫作“二分法”。芝诺说,任何一个物体要想由A点运行到B点,必须首先到达AB的中点C,而要想到达C点,又必须首先到达AC的中点D,要想到达D点,则必须到达AD的中点,等等。这个二分过程可以无限地进行下去,这样,该物体就不可能离开A点运动哪怕一丁点。这个过程可以表示如下:
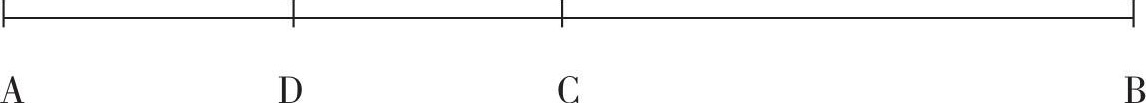
“二分法”还有一种说法:任何物体要想由A点运行到B点必先到达中点C,到了C点之后,又必须到达CB的中点D,到了D之后,又必须到达DB的中点,这样的中点有无限多个,所以,该物体无论如何到不了终点B。
第二个悖论叫作“阿喀琉斯”(又译阿基里斯)。阿喀琉斯是希腊传说中的善跑者,是特洛伊战争中的英雄。芝诺现在论证他追不上乌龟。阿喀琉斯若想追上乌龟,首先必须到达乌龟开始跑的位置,因为乌龟起跑时在阿喀琉斯的前面,有一定的距离。这个要求是合理的,但当快腿阿喀琉斯到达乌龟开始跑的位置时,乌龟已经跑到前面去了。要知道,乌龟虽然跑得慢,但它毕竟在跑。好了,等阿喀琉斯到达乌龟起跑的位置时,他若想追上乌龟又面临同样的问题:他必须先跑到乌龟此刻的位置才能追上乌龟,但等他跑到了,完全同样的问题又摆在他面前。这样的问题可以无限地出现。虽然阿喀琉斯跑得快,他也只能一步一步逼近乌龟,却永远追不上它。乌龟总是在他前头,在他与乌龟之间总有一段距离需要跑,虽然这个距离越来越短,可“总有”。
第三个悖论叫作“飞矢不动”。芝诺说,任何一个东西老待在一个地方那不叫运动,可是飞动着的箭在任何一个时刻不都是待在一个地方吗?既然飞矢在任何一个时刻都待在一个地方,那我们就可以说飞矢不动,因为运动是地方的变动,而在任何一个时刻飞矢的位置并不发生变化,所以任一时刻的飞矢是不动的。既然任一时刻的飞矢不动,那飞矢当然就是不动的。
第四个悖论叫作“运动场”,说的是运动场上三列物体的相对运动所造成的谬误。假设有A、B、C三列物体按如下方式排列:

又假定每一时间单元B和C相对于A运动一个空间单元,但方向相反。于是,在一个时间单元之后三列物体排列如下:

两个时间单元之后排列如下:
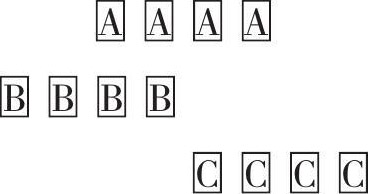
问题出现在,经过一个时间单元后,B与C相互之间有了两个空间单元的移动,经过两个时间单元后,B与C有了四个空间单元的移动。若想B与C只有一个空间单元的移动,那么对应的是半个时间单元,B相对于A移动一个空间单元需要一个时间单元,而相对于C移动一个空间单元却需要半个时间单元,这表明一个时间单元等于半个时间单元。
芝诺的这四个悖论可分为两组。头两个是第一组,假定时间空间是连续的,后两个是第二组,假定时间空间是间断的。每组的第一个悖论表明孤立物体的运动是不可能的,第二个表明两个物体的相对运动是不可能的。芝诺意在表明,无论时空是连续的还是间断的,运动都不可能,都会出现荒谬的事情。
芝诺悖论的特点是道理简单,叙述不复杂,任何人一听就明白,但其结论鲜明,出人意料。人们免不了会觉得这肯定是诡辩,一定可以找出其毛病所在。从亚里士多德开始,大多数哲学家都力图指出芝诺的论证是错误的。可令人奇怪的是,这个问题至今也未能彻底解决,许多前人指出的错误,后人发现其实并不是错误。
举四个悖论中最为有趣的“阿喀琉斯”为例。小学生都懂得如何计算阿喀琉斯追上乌龟应花的时间。设他的速度是 v 1 ,它的速度是 v 2 ,他们的初始距离是 d ,那么追上乌龟的时间是 d /( v 1 - v 2 )。既然能算出需要多长时间才能追上,我们还有什么理由说他永远追不上它呢?芝诺如果听了这样的话,一定会笑着说:“我当然知道阿喀琉斯能够追上乌龟,可是问题在于这不合道理。从道理上讲是永远追不上的。你们若想说服我,就必须把道理说出来,光举日常生活中的例子,那是没有用的。”事实上,小学生之所以能算出阿喀琉斯追上乌龟的时间,是因为他们用了一个公式,而这个公式是解如下方程得出的:
d + v 2 T = v 1 T
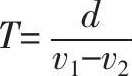
列出这个方程是很容易的,但有一个假定,那就是假定阿喀琉斯最终追上了乌龟,而且设追上的时间是 T 。这也就是说,虽然我们求出了追上乌龟的时间,但那是我们先假定能追上才得出的。并不能因为我们求出了时间,就“证明”了能追上。
现代数学运用极限理论和微积分可以得出相同的结果。我们现在把阿喀琉斯要跑的距离全部列出来:第一步,到达乌龟的起点,要跑初始距离
d
,要花时间
 ,这段时间内,乌龟又向前跑了一段距离
,这段时间内,乌龟又向前跑了一段距离
 ;于是,第二步,再跑
;于是,第二步,再跑
 ,跑这段距离要花时间
,跑这段距离要花时间
 ,这段时间内,乌龟又向前跑了一段距离
,这段时间内,乌龟又向前跑了一段距离
 ……如此算下来,可以列出一个总距离的数列:
……如此算下来,可以列出一个总距离的数列:
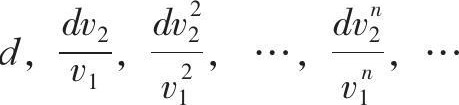
这个数列有无穷多项,但其总和并不是一个无限大的数目,而是一个有限数
 ,用它除以
v
1
,就与我们刚才运用简单公式算出的时间一样了。
,用它除以
v
1
,就与我们刚才运用简单公式算出的时间一样了。
这是不是就可以说明,芝诺只是把项的无穷多与总和的无穷大混为一谈,才造成阿喀琉斯追不上乌龟的荒谬结论呢?还不能这样说。对芝诺来说,即使总和并非无穷大,无穷多个步骤也是难以完成的。毫无疑问,阿喀琉斯越来越接近乌龟,距离越来越小,可是面对这无限多个步骤,尽管越来越容易完成,阿喀琉斯这个有限的人物,怎么可能完成?
芝诺悖论涉及对时间、空间、无限、运动的看法,它至今还在困扰着哲学家和数学家,这个难题对数学的发展有着重要的积极意义。

留基伯画像
自泰勒斯提出“万物源于水”这个命题以来,自然哲学家们相继发展出了对自然现象进行说明的理论。早期的人们都把自然现象归于某种单一的自然物质,如水、气、火等,这种做法虽然完成了对自然界的统一解释,但并不令人信服。人们都知道,自然界中既有水,也有火。但常言说得好,水火不相容,它们分明是两种完全不同的东西,为什么水本质上就是火,或者反过来,火本质上就是水呢?如此看来,用单一的自然物质作为自然界统一的基础是行不通的。自然界的现象和事物是复杂多样的,将“多”统一成“一”是不大容易的。特别是在现象的层次上,更是不能服人。由于“多”与“一”的矛盾不能解决,科学思想的概念基础不能牢固建立,科学的大发展就不可能。
原子论者留基伯、德谟克利特是爱奥尼亚人。前者生于米利都,后者生于希腊北部的阿布德拉。他们提出了科学思想史上极为重要的原子论。原子论主张,世界是统一的,自然现象可以得到统一的解释,但统一不是在宏观的层次上进行的,不是将一些自然物归结为另一些自然物,而是将宏观的东西归结为微观的东西。这些微观的东西就是原子。

布吕根
把一个物体一分为二,它变得更小,但仍然是一个物体,还可以被一分为二。这个过程是否可以无限地进行下去呢?原子论者说,不能。分割过程进行到最后,必然会有一个极限,这个极限就是原子。所谓原子,在希腊文中原意就是不可再分割的东西。原子太小,我们看不见,但世界上的万事万物都是由原子构成的,世界的共同基础是原子。
为什么世界上各种事物会彼此不一样呢?原子论回答说,这是因为组成它们的原子在形状、大小、数量上不一样。这个回答看似平常,但非同一般。我们知道,世界上丰富多彩的事物之所以难于统一,原因在于,它们看起来彼此有质的区别。原子论把这些质的区别还原成量的差异,就使统一的自然界可以用数的科学来描述。我们知道数学在今天对于自然科学是必不可少的,之所以会这样,是因为有原子论这样的思想基础。
原子论在希腊时代还只是思辨的产物,主要是一种哲学理论,不是科学理论。原子论者留基伯和德谟克利特本人并不是科学家。但是作为一种杰出的科学思想,原子论有其重要的历史地位。近代科学重新复兴了原子论,并在实验基础上构造了物质世界的原子结构。今天,“原子”不再是一种哲学的思辨,而是一个物理学概念。物质由分子构成,分子由原子构成,而原子则由原子核和核外电子组成。20世纪,人们对原子核的内部组成又有了新的发现。这一切科学成就都源于2500年前古希腊原子论者的天才构想。
有人类生活的地方就有医学。希腊文明作为一种高度发达的文明,不仅有医生和医药,而且有成系统的医学体系。创造医学体系最早的要数爱奥尼亚地区柯斯岛上的希波克拉底。以他的名义流传下来的著作集成《希波克拉底全集》
 ,共有大约60篇或长或短的文章(不同的辑本篇数不同)。人们倾向于认为,这些文章并不都是他一人所写,可能汇集了许多人的工作,但由于他生前即已德高望重、闻名遐迩,故都托他之名。
,共有大约60篇或长或短的文章(不同的辑本篇数不同)。人们倾向于认为,这些文章并不都是他一人所写,可能汇集了许多人的工作,但由于他生前即已德高望重、闻名遐迩,故都托他之名。

希波克拉底雕像,藏于牛津自然博物馆。吴国盛摄
希波克拉底大约于公元前460年出生在柯斯的一个医生世家。柯斯是一个有着悠久医学传统的小岛,医生在那里受到尊重。希波克拉底从小就受到了良好的教育,据说他到处求学,是智者高尔吉亚的学生,还是原子论者德谟克利特的朋友。成年之后,他在希腊各地为人治病,由于他在从医方面的杰出贡献,雅典特别授予这位外邦人“雅典荣誉公民”的称号。
希波克拉底最大的贡献是将医学从原始巫术中拯救出来,以理性的态度对待生病、治病。他注意从临床实践出发,总结规律,同时也创立了自己的医学理论,即体液理论。希波克拉底认为,人身上有四种体液,即血液、黄胆汁、黑胆汁和黏液,这四种体液的流动维系着人的生命。它们相互调和、平衡,人就健康,如果平衡破坏,人就生病。这种体液理论一直在西方医学中流传,就像中医的阴阳五行说一样,成了西医的理论基础。
希波克拉底不仅以医术高超著称,而且以医德高尚为人称道。在他周围,形成了一个医学学派和医生团体。他首创了著名的希波克拉底誓词,每一个想当医生的人都要以此宣誓。誓词中说,医生要处处为病人着想,要保持自身行为和这一职业的神圣性。
希波战争使爱奥尼亚的希腊殖民城邦相继陷落。爱奥尼亚的文化精英们大都逃到了雅典。这股东学西渐的潮流不久就导致了雅典文化的黄金时代。希波战争的胜利加强了雅典在希腊世界的地位,政治上的优势带来了经济上的繁荣,经济上的繁荣促进了文化的发展。这一时期,雅典的民主体制获得了空前的发展机会。人们热衷于谈论政治,谈论法律和规则。辩论术盛行,辩论术士也颇受青睐。在这种特殊的条件下,雅典出现了智者学派(Sophist,中文也译作“巧辩学派”或“诡辩学派”)。这是一群靠卖弄口舌谋生的人。他们有的教富家子弟辩论,有的直接在法庭上帮人辩护打官司,很像我们今天的律师。在一般哲学史中,智者被认为是希腊哲学史上由自然哲学向人文哲学转变的一个转折点。从他们开始,希腊哲学家关注的主要问题由自然转向人。智者普罗泰哥拉的名言“人是万物的尺度,是存在的事物存在的尺度,也是不存在的事物不存在的尺度”,表明智者对人的问题的关心已胜过自然问题。不过,这只是问题的一个方面。要知道,对希腊人而言,自然与人的对立并不像近代世界那样严重。这里我们要特别提到,关注人的问题的智者,同样在希腊数学史上占据一席之地。
智者在巧妙、娴熟地运用概念的过程中,促进了逻辑思维的发展。他们之中有许多是著名的几何学家,希腊数学三大难题就是他们提出来的。这三大难题是:
(1)化圆为方,或说,求圆面积。
(2)2倍立方,或说,求一立方体之边,使其体积等于已知边长的立方体的2倍。
(3)三等分任意角。
这三个题目看起来并不困难,为什么会成为希腊数学三大难题呢?实际上,所谓的难题是相对于一定条件来说的,离开条件限制难题就不一定成为难题。对这三个问题,希腊数学家要求只运用直尺和圆规两个工具来解决,这正是难点之所在。
试看第二个难题2倍立方。这个问题可以等价为用尺规做出长度
 来,可是,从那时以来的2000多年,几何学家都没能做出来。笛卡尔最早指出这是一个不可能做出的题目。法国数学家范齐尔于1837年严格证明了用尺规不能做出来。但如能运用别的几何工具,或运用别的数学方法,解决这个问题是不难的。
来,可是,从那时以来的2000多年,几何学家都没能做出来。笛卡尔最早指出这是一个不可能做出的题目。法国数学家范齐尔于1837年严格证明了用尺规不能做出来。但如能运用别的几何工具,或运用别的数学方法,解决这个问题是不难的。
三等分任意角,难在任意,并非不能用尺规三等分所有的角。比如90°角,就完全可以用尺规三等分。但可以证明存在无限多个不能用尺规三等分的角。当然,抛开尺规的限制,用几何方法三等分任意角是不难的。

雅典集市的柱廊。吴国盛摄
化圆为方,实际上是要做出
 ,可是
,可是
 不是任何整系数代数方程的根,因而不可能用尺规做出。这个严格的证明是1882年由德国数学家林德曼做出的。
不是任何整系数代数方程的根,因而不可能用尺规做出。这个严格的证明是1882年由德国数学家林德曼做出的。
据说,阿那克萨哥拉最先试图解这三个难题。他晚年在牢房里(上文提到,阿那克萨哥拉被雅典人视为异端,投入监狱)还在研究化圆为方的问题。解这些问题最有名的是智者希匹阿斯(生于公元前460年),他设计了割圆曲线来完成三等分角的工作,但这种曲线并不能用尺规做出,所以不能真正解决问题。
为什么希腊数学家那么严格限制尺规做图呢?一般解释是,希腊人要求逻辑简单明了。直线和圆周是最基本的几何图形,把所有的几何图形化成这两种基本几何图形的组合,是希腊几何学家的理想。实际情况是,在智者提出这三大难题时,对尺规做图的要求并不太严格,只是因为智者好出怪题,才定下这么一个要求。后来这个要求之所以逐步成了希腊数学家自觉遵守的规则,可能与柏拉图的哲学有关系。柏拉图把几何图形理想化,反对用更多的机械工具来从事几何研究。受他的影响,希腊几何学家也尽量少用机械工具,但直线和圆周是最基本的几何构图,故限于直尺和圆规。

雅典艺术学院门前的苏格拉底坐像。吴国盛摄
对做图的重视是希腊几何学的一大特色。一个图形必须构造出来,否则就不能成为几何研究的对象。有一个关于苏格拉底与几何学家的故事,可以对这一点提供佐证。苏格拉底是柏拉图的老师,本人终生待在雅典。他没有留下著述,但他的活动和学说都由他的学生柏拉图记了下来。他奔走于雅典的大街小巷,逢人便谈,对那些自命不凡者予以巧妙的讽刺和挖苦。他最富传奇色彩的两套对话方法是“助产术”和“苏格拉底讽刺”。所谓“助产术”,是对待好学的年轻人的方法。苏格拉底从具体事例出发,逐步引导对方弄懂本来不知道的一般概念。据说苏格拉底的母亲是一个助产婆,这启发他发明了这套谈论方法。所谓“苏格拉底讽刺”,是对待自觉有知而实则无知者的方法。苏格拉底佯装自己无知,从对方已经认定的概念出发,沿着对方的思路提出一系列问题,结果使对方陷于自相矛盾的境地。苏格拉底对这些方法的运用,在柏拉图写的对话中得到了生动的反映。
有一天苏格拉底与一位几何学家谈论“全体大于部分”这个几何学公理。他设计了这样一个题目,使几何学家大吃一惊:先画一个正方形 ABCD ,然后在外侧引一条与 AB 等长并与之成锐角的线段 AE 。连 CE 并做 CB 、 CE 的中垂线,两条中垂线交于 O 点。连 OA 、 OE 、 OB 、 OC 、 OD ,不难得知 OD = OA , OC = OE , CD = AE ,因此△ OCD =△ OEA 。由此可以得出∠ ODC =∠ OAE ,∠ ODC -∠ ODA =∠ OAE -∠ OAD 。由于∠ ODA =∠ OAD ,故而有∠ ADC =∠ DAE ,也就是∠ DAB =∠ DAE 。证明到了这一步,几何学家也不知如何是好,竟不得不承认有的时候全体并不是大于部分而是等于部分。他说:“啊,苏格拉底,看来数学上的真理也常常并不是那么一回事,有时竟是虚构的,这一点已经被你证明了!”
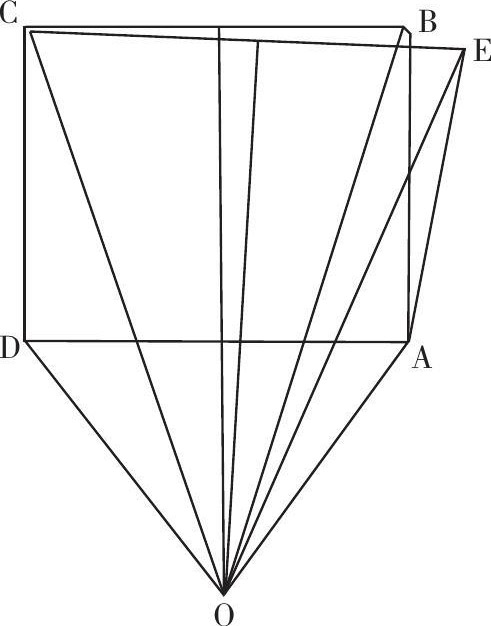
苏格拉底当然没有证明部分等于全体,在这里他不过是同几何学家开了一个玩笑。读者可以自己思考一下,苏格拉底证明的问题出在哪里?

雅克-路易·大卫(Jacques-Louis David,1748—1825)1787年创作的油画《苏格拉底之死》
雅典最著名的天文学家是默冬,他继阿那克萨哥拉之后从事天文观测。公元前432年的奥林匹克竞技会上,默冬宣布了他的发现,即19个太阳年与235个朔望月的日数相等。这个周期在我国被称为章,所以默冬周期也常译成默冬章。有了这个周期,就可以确定阴阳历中的置闰规则。235个朔望月的总日数是6940,19年中必有12年是平年,7年是闰年。19年7闰的置闰法在我国被称为章法,它的发现标志着希腊天文观测已达到很高的水平。

雅典普尼克山上默冬的太阳钟遗址。吴国盛摄

柏拉图的大理石头像
雅典学术在柏拉图这里走向系统化。柏拉图出生于雅典的名门世家,他的母亲是梭伦的后裔,父系则可以追溯到古雅典王卡德鲁斯。在这样一个高贵的家庭里,柏拉图从小就受到了当时的人可能受到的最好的教育。年轻的柏拉图立志从事政治,他参加过伯罗奔尼撒战争,表现得十分勇敢。他是苏格拉底最好的学生。传说在他成为苏格拉底学生的头天晚上,苏格拉底梦见一只天鹅来到膝上,很快羽翼丰满,唱着动听的歌儿飞走了。这个传说生动地反映了苏格拉底与柏拉图之间的亲密关系。柏拉图留下的众多对话,大都是以苏格拉底为主要角色。这位可亲可敬的老师却因“败坏青年”等罪状被雅典的民主体制判处死刑。这件事对柏拉图影响很大,他从此决定不再参加政治活动,因为政治太丑恶、太肮脏了。
苏格拉底死后,柏拉图离开了雅典,周游世界。他先到了埃及,后来又到了南意大利,在那里认真研究了毕达哥拉斯学派的理论。柏拉图在外游历十年后,约于公元前387年回到了雅典。雅典西北郊有一座以英雄阿卡德米命名的圣城。这里自古就是一个公共体育场,柏拉图家族在附近有一座别墅。正当盛年的柏拉图决定在此开设学园,招生讲学。学园的主要目的是促进哲学的发展,但是为了进入哲学,还需要学习许多预备课程,这些课程包括希腊数学的诸种学科:几何学、天文学、音乐学、算术等。据说,柏拉图叫人在学园的门口立了一块牌子:“不懂数学者不得入内”,表明他对数学十分重视。

雅典西北郊的阿卡德米遗址,如今是一个公园。吴国盛摄
柏拉图本人的哲学受毕达哥拉斯学派影响很大,许多人甚至把他视作毕达哥拉斯学派的人。在柏拉图的哲学中,有一种神圣和高贵的东西,追求纯粹的理想是他的一大特色。他相信,真正实在的不是我们日常所见、所闻的种种常识和感觉。这些东西千变万化,转瞬即逝,是不牢靠的。真正的实在是理念。哲学的目的就是把握理念。理念先于一切感性经验,具有超越的存在,日常世界只是理念世界不完善的摹本。任何一张桌子都有这样或那样的缺陷,不足以代表真实的桌子。只有桌子的理念才是完美无缺的。在诸多自然事物中,数学的对象更具有理念的色彩,虽然它也还不是理念本身。比如,我们所见到的任何一个圆显然都不是真正的圆,谁也不能说自己画得足够圆;我们所见到的任何一条直线也不是真正的直线,因为真正的直线没有宽度,没有任何弯曲。真正的圆和真正的直线不是我们感觉经验中的圆和直线,而是圆的理念和直线的理念。它们是最容易领悟的理念,因此,通过研究直线和圆这些几何对象更容易进入理念世界。在柏拉图看来,数学是通向理念世界的准备工具,所以在他的学园里,数学研究得到了极大的发展,他的学生中出了不少大数学家。

瑞典画家卡尔·约翰·瓦尔布姆(Carl Johan Wahlbom,1810—1858)创作的雅典学园,柏拉图正在给学生们讲课。
柏拉图本人对数学的贡献不详,但他对于数学演绎方法的建立和完善肯定起了重要的作用。在《理想国》中,柏拉图谈到应该重视对立体几何的研究,而且他已经知道正多面体最多只有五种,即正四面体、立方体、正八面体、正十二面体和正二十面体。此外,最重要的发现是圆锥曲线。他们用一个平面去截割一个圆锥面,角度不同会得出不同的曲线:当平面垂直于锥轴时,得到圆;平面稍稍倾斜一点,得到椭圆;平面倾斜到与圆锥的一条母线平行时,得到抛物线;平面与锥轴平行时得到双曲线的一支。

13世纪晚期法国流传的一幅画
柏拉图的学生中在数学上最有成就的是欧多克斯。他大约于公元前368年才加入柏拉图的学园。那时,他已经功成名就,周围有一些弟子。欧多克斯在数学上的主要贡献是建立了比例论。越来越多的无理数的发现迫使希腊数学家不得不去研究这些特殊的量,欧多克斯的贡献在于引入了“变量”的概念,把数与量区分开来。在他看来,(整)数是不连续的,而量不一定如此,那些无理数都可由量来代表。数与量的区分方便了几何学的研究,为数学研究不可公度比提供了逻辑依据。但是,人为地将数从几何学中赶出去,使数学家们不再关心线的长度,不再关心算术,而把精力全部投入到几何学中。
欧多克斯更重要的贡献在天文学方面。柏拉图与毕达哥拉斯一样深信,天体是神圣和高贵的,而匀速圆周运动又是一切运动之中最完美、最高贵的一种,所以,天体的运动应该是匀速圆周运动。可是,天文观测告诉我们,天上的有些星星恒定不动地做周日运转,而有些星星却不是这样。它们有时向东,有时向西,时而快,时而慢。人们把这些星称作行星(在希腊文中,行星planets是漫游者的意思)。柏拉图对这种表观的现象和流行的叫法不以为然,他相信就是行星也一定遵循着某种规律,像恒星一样沿着绝对完美的路径运行。因此,他给他的门徒提出了一个任务,即研究行星现在这个样子究竟是由哪些匀速圆周运动叠加而成的。这就是著名的“拯救现象”方法。“拯救”的意思是,行星的现象如此无规则、如此“不体面”,只有找出其所遵循的规则的、高贵的运动方式,才能洗刷这种“不体面”。
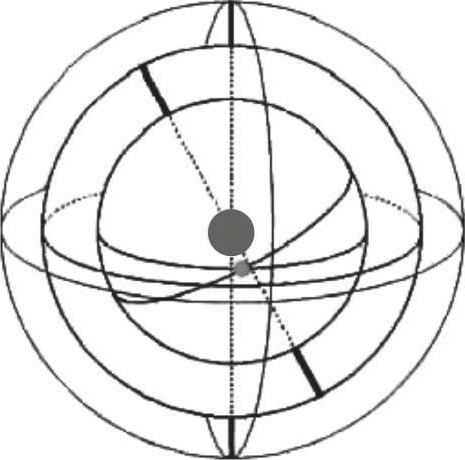
欧多克斯的同心球模型
欧多克斯为柏拉图的理想提供了第一个有意义的方案,即同心球叠加方案。按照这个方案,每个天体都由一个天球带动沿球的赤道运动,而这个天球的轴两端固定在第二个球的某个轴向上,第二个球又可以固定在第三个球上,这样可以组合出复杂的运动。欧多克斯发现,用3个球就可以复制出日月的运动,行星的运动则要用4个球。这样,五大行星加上日月和恒星天,一共需要27个球。通过适当选取这些球的旋转轴、旋转速度和半径,可以使这套天球体系比较准确地再现当时所观测到的天体运动情况。
欧多克斯设计的这套天球体系建立在毕达哥拉斯学派的宇宙图景基础之上,用天球的组合来模拟天象,是希腊数理天文学的基本模式。当然,欧多克斯的体系与实际情况结合得还不太好,后人对此有诸多改进,但他这条思路,被完全继承下来了。
“拯救现象”是一种科学研究的纲领。我们面对的自然界纷纭复杂、变化万千,如果不把它们纳入一个固定的框架之中,我们便不能很好地把握它们。拯救现象,正是将杂乱的现象归整。近世的研究者注意到,力图将天空中的漫游者固定起来或使其规则化,是与希腊当时的一个社会问题相对应的。在当时的雅典,有许许多多的流浪者游手好闲,到处闯荡,使当政者感到头痛。希波战争期间,强行征募这些游民入伍,接受军队的规范和制约,较好地解决了这一社会问题。将这件事情与柏拉图的拯救现象相类比当然是有趣的。我们虽然无法确定柏拉图是否正是从当局治理游民问题得到启发从而提出了拯救现象纲领,但希腊时代对人与自然并无严格的区分,对自然现象的“拯救”与对社会秩序的维护确实具有类似的意义。
柏拉图的学园培养了许多优秀的人物,亚里士多德就在这里当过学生。柏拉图在世时,一直亲任学长。他去世之后,由他的外甥斯彪西波担任第二代学长。学园后来虽然在学术上没有什么大的建树,但作为希腊文化的保存者存在了900余年,直到公元529年才被东罗马皇帝查士丁尼勒令关闭。阿卡德米(Akademia)后来成了学院、研究院、学会(academy)的代名词。

亚里士多德的大理石头像
柏拉图之后,亚里士多德成为希腊世界最伟大的思想家、哲学家和科学家。公元前384年,亚里士多德生于希腊北部的斯塔吉拉,其父尼各马可是马其顿王阿明塔二世的御医。亚氏幼年时父母双亡,由亲戚抚养长大,17岁那年来到雅典,进入柏拉图的学园学习,直到柏拉图去世才离开,前后达20年。在这里,他受到了良好的教育。据说柏拉图很器重他,但是他并没有留在学园里继承柏拉图的“衣钵”,而是自己创立了与柏拉图非常不同的哲学体系。对此,他说了一句名言:“我敬爱柏拉图,但我更爱真理。”今日我们常说的“吾爱吾师,吾尤爱真理”是这一名言的另一种翻译。公元前343年,马其顿王腓力邀请亚里士多德做13岁的太子亚历山大的私人教师。这位亚历山大长大之后,南征北战、所向披靡,成了世界历史上著名的亚历山大大帝。公元前335年,亚里士多德回到了雅典,在吕克昂建立了自己的学园。在这里,他从事教学和著述活动,创建了自己的学派。吕克昂有一座花园,他和他的学生们常常在花园里边散步边讨论学术,人们因而称他们是逍遥学派(Peripatetic)。公元前323年,亚历山大大帝去世,雅典人开始密谋反马其顿的行动。亚里士多德曾经是亚历山大的老师,因此受到牵连,不得不离开雅典。他将学园付托给他的学生特奥弗拉斯特,回到了他母亲的母邦卡尔西斯,次年在那里病逝,终年63岁。

吕克昂遗址。吴国盛摄
如果说柏拉图是一位综合型的学者,亚里士多德就是一位分科型的学者。他总结了前人已经取得的成就,创造性地提出自己的理论。在几乎每一学术领域,亚里士多德都留下了自己的著作。从第一哲学著作《形而上学》,物理学著作《物理学》《论生灭》《论天》《气象学》《论宇宙》,生物学著作《动物志》《动物的历史》《论灵魂》,到逻辑学著作《范畴篇》《分析篇》,伦理学著作《尼各马可伦理学》《大伦理学》《欧德谟斯伦理学》,以及《政治学》《诗学》《修辞学》等,他的著作几乎遍及每一个学术领域,他是一位名副其实的百科全书式的学者。
亚里士多德的哲学博大精深,自成一体。他不同意柏拉图的理念说,认为事物的本质寓于事物本身之中,是内在的,不是超越的。为了把握世界的真理,必须重视感性经验。就对待自然界的态度而言,这是与柏拉图完全不同的。柏拉图强调理念的超越性,蔑视经验世界,他发展了数学;而亚里士多德重视经验考察,特别在生物学领域取得了卓越的成就。他的哲学目的在于找出事物的本性和原因,因而发展了一套“物理学”,以穷究事物之道理。

德国弗莱堡大学的亚里士多德铜像。吴国盛摄
在天文学方面,亚里士多德走的还是欧多克斯的路子,即通过天球的组合来解释天体的表观运动。有所不同的是,亚里士多德不限于“拯球现象”,他还给出了天体运动的物理解释。欧多克斯的学生卡里普斯在原来27个天球的基础上又添加了7个球,以获得与天文观测更精确相符的结果。亚里士多德在卡里普斯的基础上又添了22个天球。新添的天球,并非为了更准确地与观测相符,而是为了使这个天球体系形成一个有物理联系的整体。他要实现的是最外层天球作为原动天——也就是第一推动——对整个天球系统的物理支配。新添的天球既用以保证外层的天球将周日运动传给内层的天球,又防止外层天球将多余的运动传给内层。亚里士多德认为,天体与地上物体本质上是两种不同的物质。天体由纯洁的以太组成,是不朽和永恒的,它的运动是完美的匀速圆周运动。
至于地上物体,涉及的是物理学的内容。亚里士多德认为,地上物体由土、水、气、火四种元素组成,其运动是直线运动。地上物体都有其天然的处所,而所有的物体都有回到其天然处所的趋势。这一趋势即所谓的天然运动。土和水本质上是重性的,其天然处所在下,因此它们有向下的天然运动;气和火本质上是轻性的,其天然处所在上,因此它们有向上的天然运动。重性越多,下落速度越快,所以重物比轻物下落得快。除了天然运动外,还有受迫运动。受迫运动是推动者加于被推动者的,推动者一旦停止推动,运动就会立刻停止。比如马拉车,车运动;马一停止拉车,车就不再动了。在自然界中,亚里士多德也发现了等级之分。轻的东西比重的东西高贵,天比地高贵,推动者比被推动者高贵,灵魂比身体高贵。这是亚里士多德物理学中很有特色的东西。

海耶兹
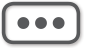
亚里士多德哲学中的四因说对于理解他的生物学成就是有用的。他认为,事物变化的原因有四种,一是质料因,二是形式因,三是动力因,四是目的因。比如一座铜制的人物雕像,铜是它的质料因,原型是它的形式因,雕刻家是它的动力因,它的美学价值是它的目的因。目的因又称终极因,是最重要的。自然界的事物都可以用目的因来解释:重物下落是因为它要回到天然位置上去;植物向上长因为可以更接近太阳,吸收阳光;动物觅食因为饥饿;人放声大笑因为喜悦等。这种目的论的解释具有很浓的拟人色彩,用于物理世界显得十分幼稚可笑,但对于生物学并不是完全没有意义的。
亚里士多德的生物学著作也许是他的科学工作中最有价值的。在这些著作中,他完全以一个近代生物学家的姿态去观察、实验、总结生物界的现象和规律。据说亚里士多德很注意搜集第一手材料。他亲自解剖动物,观察它们的习性。《动物志》中对各种各样动物的详尽描述,就是他长期观察的结果。他注意到“长毛的四足动物胎生,有鳞的四足动物卵生”,认识到“凡属无鳃而具有一喷水孔的鱼,全属胎生”。他还对人类的遗传现象做过细致的观察,如注意到一个白人女子嫁给一个黑人,子女的肤色全是白色的,但到孙子那一代,肤色有的黑,有的白。
亚里士多德去世后,吕克昂学园由特奥弗拉斯特主持。特氏延续了老师对生物学的研究工作,特别在植物学上做出了重要的贡献。特奥弗拉斯特之后,学园由斯特拉图主持。斯氏主要发展了亚里士多德学说中物理学的方面,把实验方法运用到了物理学领域。为了探讨真空问题,斯特拉图还动手制造了不少仪器。他的工作对亚历山大里亚时期的科学家有重要的影响。
任何一个古老的文明都可以通过其建筑反映出来。建筑不仅是技术的标志,也是精神风格的象征。从公元前2000年克里特文化时期的米诺斯王宫,到公元前1400年迈锡尼文化时期的卫城,可以依稀看出希腊建筑的宏伟气象。迈锡尼古城遗址狮子之门那巨大的石块,给人以威风凛凛之感。古典时代最重要的建筑都出在雅典。当时的雅典已成为希腊各邦盟主,盟国的贡赋给它带来了大量的物质财富,因而有能力建造巨大的工程。雅典城南面的巴台农神庙(雅典娜处女庙)是雅典建筑最杰出的典范。它始建于公元前480年,因希波战争受损,再建于公元前447年。它的基座长68米,宽30米,基座上耸立着56根10多米的柱子。高大华丽的列柱是希腊建筑特有的风格。希腊人喜用柱廊,经长期发展形成了多利亚、爱奥尼亚和科林斯三种风格。到了雅典时期,多利亚式和爱奥尼亚式最为流行。多利亚式建筑庄严朴实,其石柱不设柱基,柱身上细下粗,并刻有凹槽。爱奥尼亚式建筑明快活泼,其石柱下有基座,上有盖盘,柱身细长,凹槽密集。巴台农神庙是典型的多利亚风格建筑。
希腊的柱式建筑别具一格,对日后整个西方建筑的发展有着重要的影响。

巴台农神庙。吴国盛摄