数据与变量

到目前为止，我们使用了很多次“数据”这个词。但是，在日常生活中，“数据”却是一个很暧昧的词，往往会成为误解的根源。我们再来了解一下“数据”与“变量”的定义。

例如：【例题1-1】中A组6个人的考试分数分别为：

50　　 60　　 40　　 30　　 70　　　　50（分）

这6个数值组成的整体被称为“数据”，而测量对象对应的单个条目（例题中为考试分数）被称为“变量”。

注：变量也被称作“变数”。在统计学上，严格来说变量与变数是两个用途不同的术语，但在本书范围内可以通用。

实质型数据

“实质型数据”也被称作“分类数据”。例如血型、喜欢的食物、所支持的政党等无法用数字来衡量的变量（实质变量）所组成的数据。实质型数据（分类数据）即便每个项目都有编号，比如“1：A型、2：B型、3：O型、4：AB型”或“第1名：汉堡肉、第2名：拉面、第3名：寿司、第4名：烤肉”等，但是将这些数据进行加减运算的话却完全没有意义。

注：本书之后不再涉及实质型数据。

量化数据

当一些变量（量化的变量）做加减运算有意义时，由这些变量组成的数据被称作“量化数据”。量化数据可以被细分为两个类别，分别为：骰子的数字、汽车的数量、人数等只能取跨越型数值的数据（离散型数据）；身高、体重、时间等可以取连续数值的数据（连续型数据）。

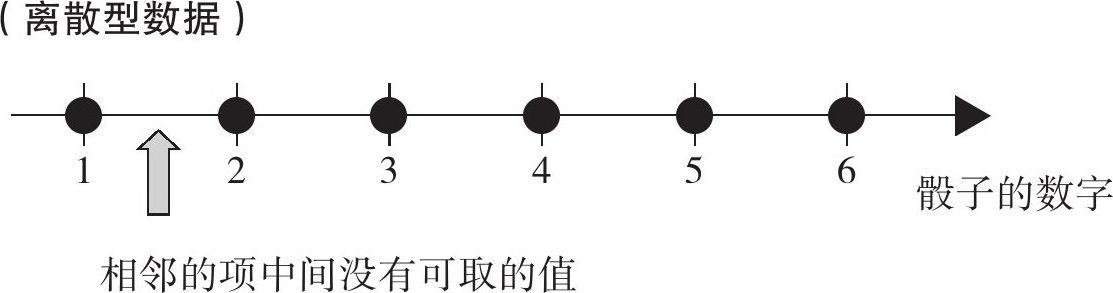
又是“离散型数据”又是“连续型数据”的，刚开始接触这两个术语的时候，可能会很不习惯，而且觉得难以理解。“离散型数据”是指两个相邻的项之间没有可取值的数据。比如骰子的数字1和2之间没有“1.5”，或者对汽车的数量进行计数时，10辆与11辆之间也没有“10.5辆”。将数据放在数轴上时，只能取跨越型数值的数据是“离散型数据”。

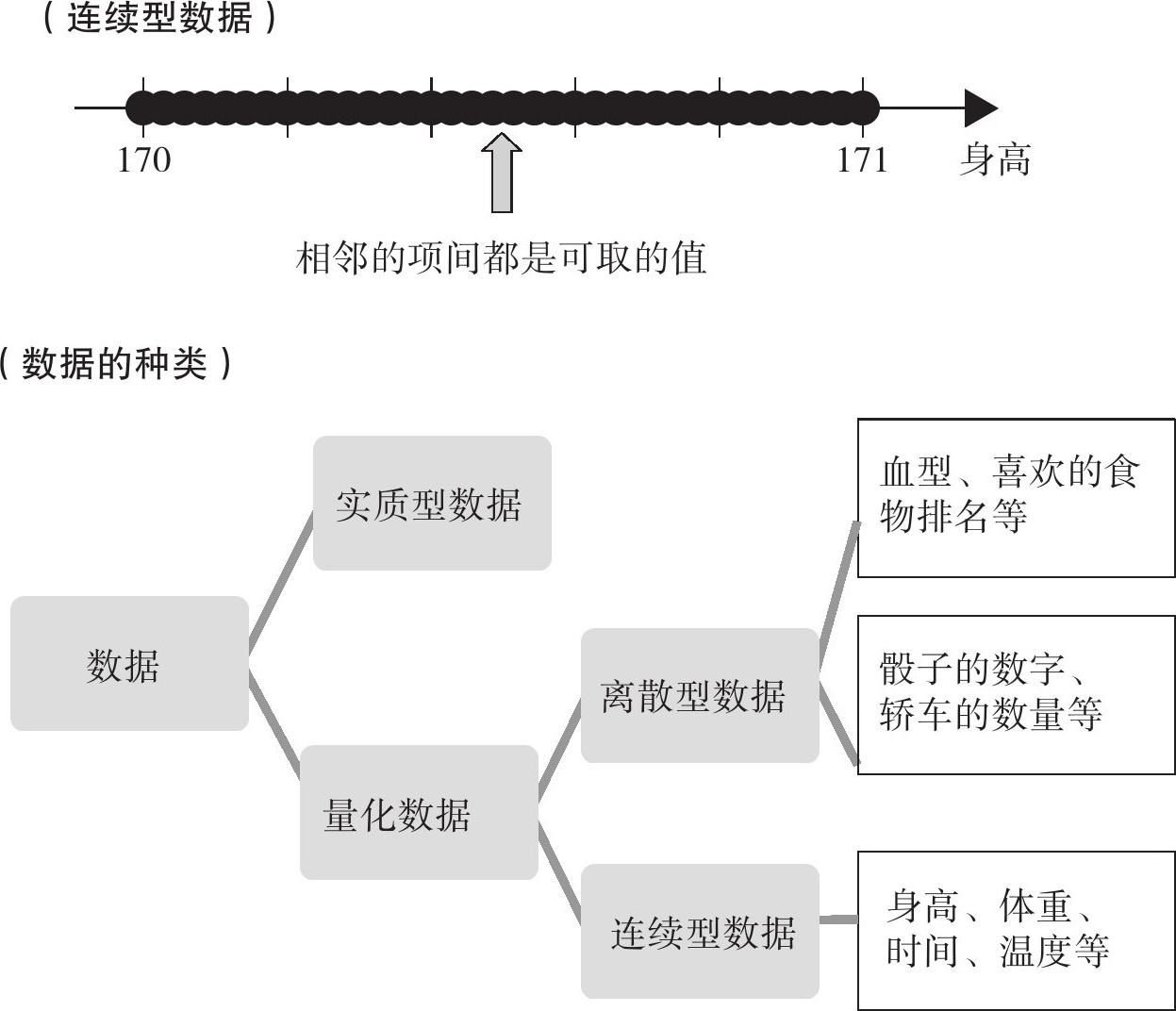
但是，测量身高时，在170cm与171cm之间，有身高为170.5cm的人是很正常的事，而且，如果对测量结果要求严格的话，在170.5cm与170.6cm之间，还会有身高170.55cm的人。像这样，不管怎么细分，永远都有更多可取数值的数据为“连续型数据”。

整理数据时，最基本的步骤如下：

频数分布表

首先，我们先来看几个术语。

·组：将数据以相同间隔分开的区间。

·组中值：各组上下限中间的数值。

·频数：各组中包含数值的数量。

·相对频数：各组数据频数在总频数中的占比。

·累计相对频数：逐级相对频数相加的和。

频数分布表就是将每组中的频数、相对频数、累计相对频数等做成一张表……就算这么说估计也不明白吧？

实际操作一遍就能理解了。我们这就来实际做一做。

N数学培训班对40名学生进行了突击测验（满分为100分）。测验成绩如下表所示：

N数学班的突击测验结果

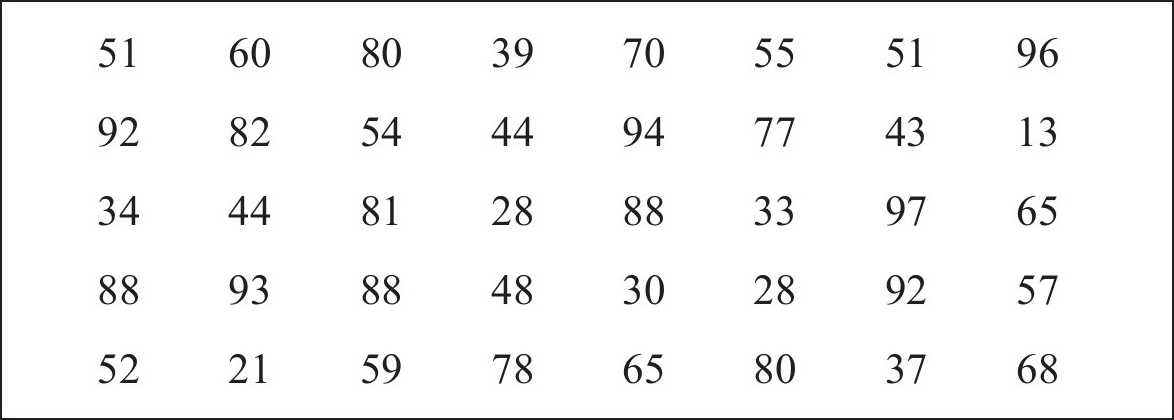
即使看了这个表，仍然无法看出数据整体的倾向与特征。于是N先生将其整理成了频数分布表。

为此我们现将数据按照分数由低到高重新排列。

N数学班的突击测验结果（按分数排列）

为了制作频数分布表，下面要做的就是决定各组的组段值。像“10～15分”“15～20分”这样，以每5分为一组，或者是“0～20分”“20～40分”这样，以每20分为一组，都可以。不过需要注意的是，每组的数值范围太小的话，表格会变得过于复杂；反之数值范围过大则无法清楚地看出数据的倾向特征。

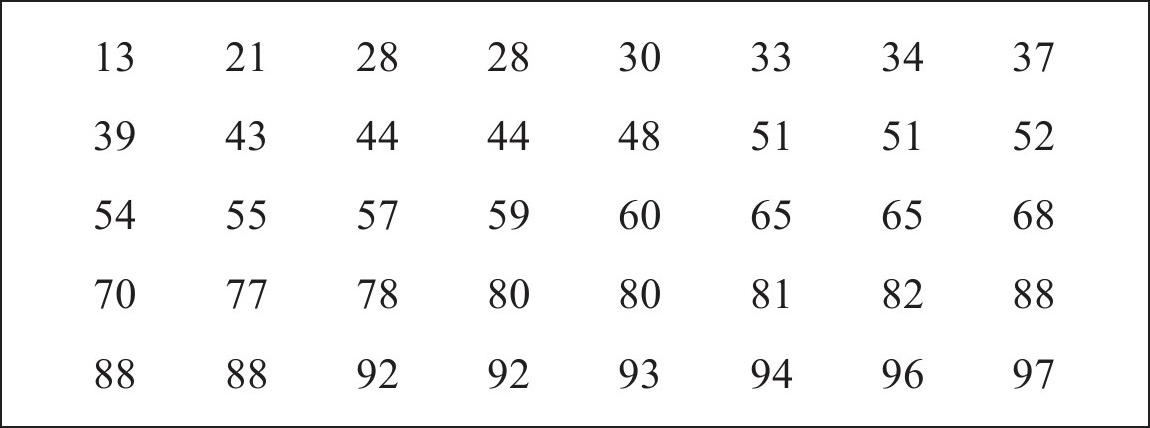
在该数据中，最低分为13分，最高分为97分，我们可以以10分间隔为一组（比如10～20分）。

N数学班突击测验的结果（频数分布表）

观察频数分布表时的注意事项

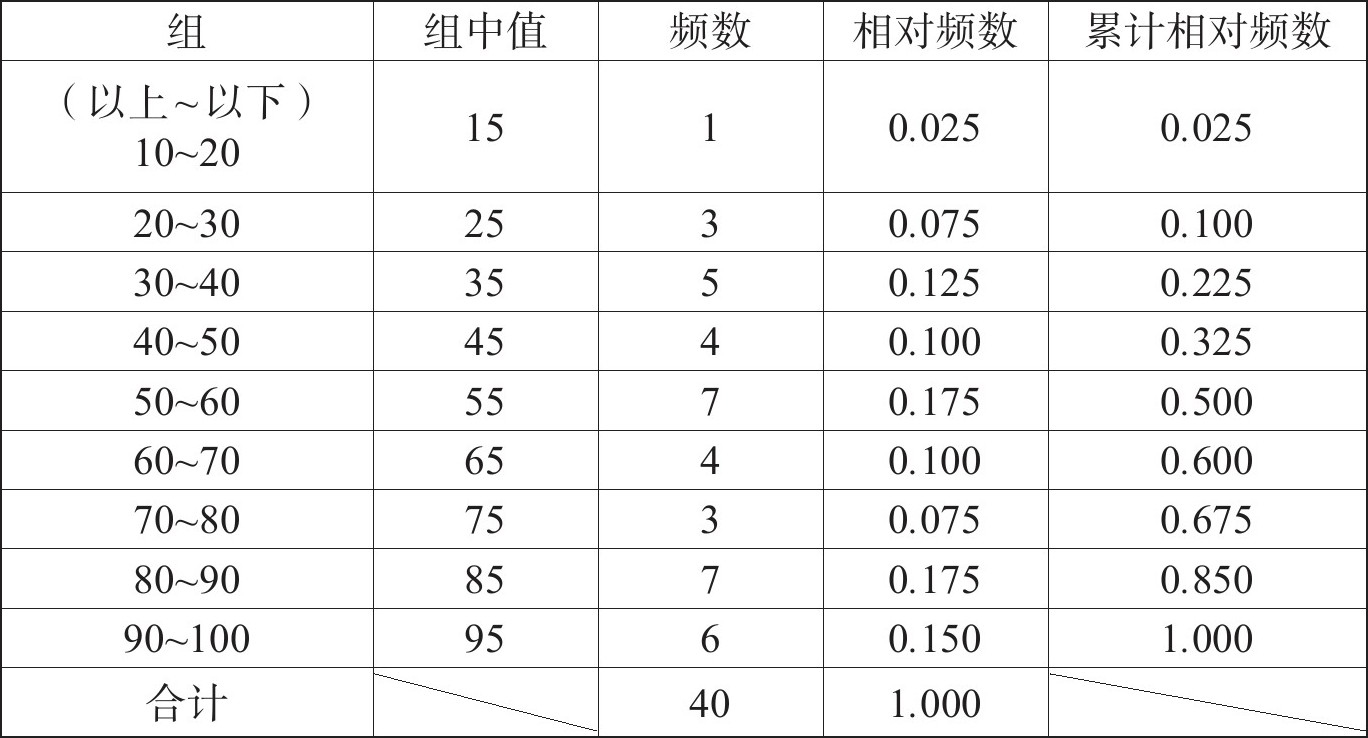
（1）频数分布表中无法体现数据中每个项目的具体数值。例如，之前的数据中，“40～50分”一组的数据中实际包括“43、44、44、48”4个数值，但是，在频数分布表中，这一组的组中值为“45”，就是说，在频数分布表中，这些数都被认为是“45”。该组数由组中值代表。

（2）相对频数是指“该组数的频数在整组数据频数中的占比”，所以计算方法是：

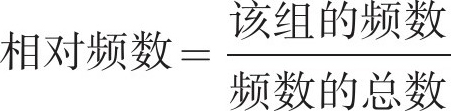
“40～50分”这一组的相对频数就是

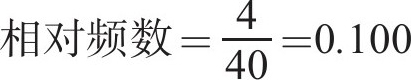
（3）除了观察“某组数据在数据总体中所占的百分比是多少”，有时候也想知道“在这组数据以下（或以上）的数，在数据总体中所占的百分比为多少”。这个时候，就需要看累计频数了。

例如，以上数据中“10～60分”这一区间的累计频数为

0.025+0.075+0.125+0.100+0.175=0.500

因为结果是0.500，所以60分以下的学生人数占了全体学生人数的50%。 Hpkcd6dvTSWrdOrB919ih5WSCWNOz+fwd7A5zzN3AL4SSLA8ZAtLjMA6JXe1unyR