




同许多科学家一样,我也不时收到记者们的采访请求,通常是一些关于城市、城市化、环境、可持续发展、复杂性、圣塔菲研究所(Santa Fe Institute)的问题和主题,偶尔甚至是关于希格斯粒子的问题。《大众力学》( Popular Mechanics )杂志的一名记者曾联系我说,好莱坞打算发行日本经典影片《哥斯拉》(Godzilla)的全新版本,她很想知道我关于哥斯拉的观点,可想而知当时我有多惊讶。你或许会回忆起来,哥斯拉是一只大多时候都在城市(在1954年的最初版中是东京)漫步的体形巨大的怪物,它会带来破坏和浩劫,并给当地老百姓带来恐怖感。
这名记者曾经听说我对比例关系有一些研究,她希望以一种有趣、滑稽且书呆子的方式阐述哥斯拉的生命机理(配合新电影的上映)……如此庞大的动物能走多快,它的新陈代谢会产生多少能量,它的体重有多少,等等。不消说,这个21世纪全新的美国式哥斯拉是这一角色迄今为止最大的化身,达到了350英尺的高度,是日本最初版哥斯拉的两倍多,后者“只有”164英尺高。我立即做出回应,告诉那名记者,她所能联系到的几乎任何一位科学家都会告诉她,像哥斯拉这样的怪兽根本不可能存在,原因在于,如果它也是由构成人体(所有生命)的基础材料构成的,它不可能正常运转,而会因自己的体重而崩塌。
早在400多年前现代科学刚刚开端时,伽利略便已经阐明了这一论断的科学依据。它在本质上是简单的关于规模缩放的论断:伽利略曾经发问,如果你尝试无限度地按比例扩大一只动物、一棵树或一栋建筑物,结果会怎么样?他的回答是,他发现增长是有限度的。他的论点确定了今天所有有关比例参数研究的基础模板。
人们在提到伽利略时,通常把他称作“现代科学之父”,这是实至名归的,他对物理学、数学、天文学、哲学做出了影响深远的贡献。或许,他最为人所知的便是在比萨斜塔塔顶所做的那个神秘实验:让两个尺寸、构成成分完全不同的物体自由落体,以证明它们最终会同时落地。这一非直观的观察与当时人们普遍接受的亚里士多德的理论相矛盾。后者认为,较重的物体的下落速度比较轻的物体快,而且下落速度与物体重量呈比例关系,这一根本性的错误观念在2 000年的时间里为人们所普遍信服,直到伽利略对其进行检验。现在回想起来,在伽利略进行研究之前,似乎没有人曾经想过,更别说动手检验这一“不言而喻的事实”了,这实在令人感到惊讶。

图2–1 35岁(左)和69岁(右)的伽利略
他在不到79岁时便去世了。我将在第4章中详细地阐述在这些画像中栩栩如生地表现出来的衰老和即将到来的死亡。
伽利略的实验彻底改变了人们对运动和动力学的认知,并为牛顿提出著名的万有引力定律铺平了道路。这些定律为理解地球乃至整个宇宙的所有运动提供了一个精确的定量化和预测性的数学框架,并由此用同样的自然规律将天空与大地统一在一起。这不仅重新定义了人类在宇宙中的地位,而且为之后的所有科学提供了黄金标准,也为即将到来的启蒙时代及过去200年的技术革命奠定了基础。
伽利略还因改良了望远镜和发现木星的卫星而闻名于世,这使他坚信哥白尼的日心说。由于继续坚持基于自己观察所得的日心说,伽利略最终付出了沉重的代价。在69岁高龄时,拖着病体的伽利略被带到罗马宗教裁判所,并被裁定为异端。他被迫放弃自己的观点,在经历短暂的关押之后,他在软禁中度过了余生(他又活了9年时间,其间还双目失明)。他的作品被禁,并登上了罗马教廷的《禁书目录》( Index Librorum Prohibitorum )。直到200多年后的1835年,他的作品才从该目录中被撤下。直到将近400年后的1992年,教皇约翰·保罗二世(John Paul II)才公开就伽利略的遭遇表达歉意。我们应该清醒地认识到,人类在很久以前是使用希伯来文、希腊文、拉丁文等语言表达基于观念、直觉甚至偏见的文字的,这要远远重于基于科学观察的证据及数学逻辑。但很不幸的是,我们今天依然无法摆脱这种被误导的思维方式。
尽管可怕的悲剧降临到了伽利略的头上,但人类从他的监禁中得到了好处。幸运的是,正是在被软禁期间,他写出了可能是他一生中最好的作品,同时也是科学文献史上真正伟大的书籍之一,这就是《关于两种新科学的对话与数学证明》(
Discourses and Mathematical Demonstrations Relating to Two New Sciences
)。
 这本书基本上是他40年来如何系统性地应对“以逻辑、理性的框架理解我们周遭自然世界”这一挑战的研究成果。就其本身而言,它奠定了牛顿所做出的同样伟大的贡献及之后许多科学成就的基础。爱因斯坦在赞扬这本书时把伽利略称作“现代科学之父”,这一点儿也不夸张。
这本书基本上是他40年来如何系统性地应对“以逻辑、理性的框架理解我们周遭自然世界”这一挑战的研究成果。就其本身而言,它奠定了牛顿所做出的同样伟大的贡献及之后许多科学成就的基础。爱因斯坦在赞扬这本书时把伽利略称作“现代科学之父”,这一点儿也不夸张。

这是一本伟大的书籍。尽管被禁,且语言和体例有些老旧,但它出人意料地具备很强的可读性和趣味性。他在书中采用了三人[辛普利西奥(Simplicio)、萨格雷多(Sagredo)、萨尔维亚蒂(Salviati)]对话的形式。在他们三人见面的四天时间里,他们就不同的大小问题展开讨论和辩论,这些问题也是伽利略希望解答的。辛普利西奥代表的是普通“外行人”,他对这个世界充满好奇,询问了一系列显而易见且幼稚的问题;萨尔维亚蒂是那个聪明的家伙(伽利略自己),知道所有问题的答案,并且以一种既引人入胜又充满耐心的方式进行了解答;而萨格雷多则是中间人,他一方面挑战萨尔维亚蒂,另一方面又鼓励辛普利西奥。
在对话的第二天,他们将注意力转移到有些晦涩难懂的有关绳索和横梁强度的问题上来。正当你思考这一沉闷乏味的、迷失方向的讨论时,浓雾渐渐散去,太阳出来了,萨尔维亚蒂做出了如下声明:
就像已经论证过的那样,你显然可以看到,不可能将艺术界或自然界中组织的规模扩大到巨大无比的尺寸;同样,也不可能建造巨大无比的轮船、宫殿或寺庙,让它们的船桨、院子、横梁、铁螺栓及其他所有部件组装在一起;自然界也不可能长出巨大无比的树木,因为树枝将会因其自身重量而断裂;同样,如果人、马或其他动物的身高无限度地增长,就无法构造出其骨骼框架并使其发挥正常的功能……因为它们自身的重量也会无限度地增长,导致它们跌倒并被自身的重量碾碎。
情况是这样的:我们有关巨型蚂蚁、甲虫、蜘蛛或者哥斯拉的不切实际的幻想早在近400年前就被伽利略猜测出来了。他当时便极为聪明地证明,它们在物理学上是不可能存在的,尽管我们可以通过动画或电影工业手段形象地将它们展示出来。或者更为精确地说,它们能够长到多大要受到基本的限制。因此,许多科幻形象真的就是虚构出来的。
伽利略的观点简单直接,却有着深远的影响。此外,其观点还为我们将在后文提到的许多概念做了很好的介绍。其观点主要包括两个部分:一个是基于几何的论据,它表明了一个物体的面积和体积随着其边长的增长而成比例增长(见图2–2);另一个是基于结构的论据,它表明了支撑建筑物的柱梁、支撑动物的四肢或支撑树木的树干的强度与它们的横截面面积是成正比的(见图2–3)。
在下面这个方框内,我描述了其观点第一部分的非技术性版本。它显示出,如果一个物体的形状是固定的,当它按比例扩大时,它所有平面的面积都按照边长的平方扩大,而它们的体积将按照边长的立方扩大。
伽利略有关面积和体积比例变化的观点
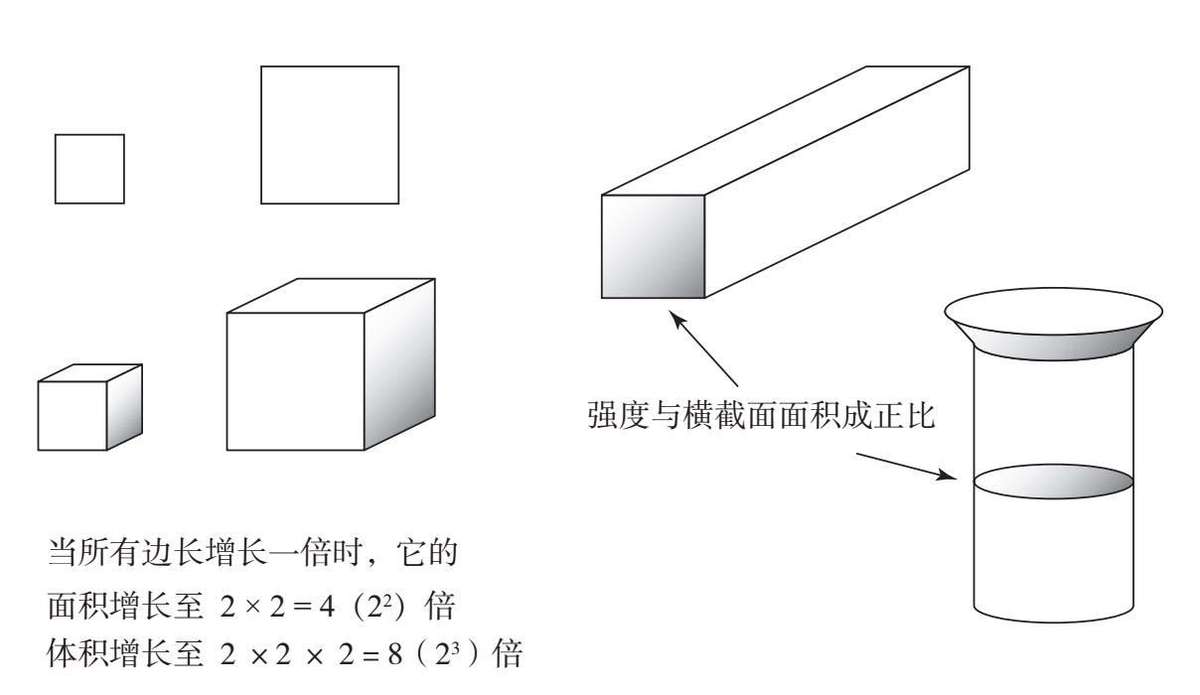
图2–2 面积和体积与边长的比例关系 图2–3 强度与横截面面积成正比
图2–2表明了正方形的面积和立方体的体积如何按比例变化。图2–3表明柱梁或肢干的强度与横截面面积成正比。
我们从最简单的几何物体开始考虑,比如一块正方形的地砖,想象一下把它按比例扩大到更大的尺寸,见图2–2。具体来说,让我们把它的边长确定为1英尺,它的面积,即相邻两边边长相乘为1英尺×1英尺=1平方英尺。现在,让我们来假设所有边长增长一倍,由1英尺变成2英尺,其面积将增长至2英尺×2英尺=4平方英尺。相似地,如果我们把边长增长至3英尺,其面积将增长至9平方英尺,以此类推。概括起来的规律是明确的:面积将按边长的平方倍数增长。
这一关系适用于所有二维几何图形,不仅仅是正方形,只要其形状是固定的,则其所有的线性尺寸都会按照相同的倍数增长。
一个简单的例子便是圆形,例如,如果其半径增长一倍,其面积将增长至原来的2×2=4倍。一个更加普遍的例子是,将你的房子的每条线的边长增长一倍,并保持其形状和结构布局不变,比如其墙面和地板等所有平面的面积将增长至原来的4倍。
这一论断可以直接从面积延伸到体积。让我们先看一个简单的立方体:如果它的边长增长一倍,从1英尺增长至2英尺,它的体积就将从1立方英尺增长至2英尺×2英尺×2英尺=8立方英尺。同理,如果其边长增长至3英尺,其体积就将增长至3英尺×3英尺×3英尺=27立方英尺。如同面积一样,这同样可以直接概括所有其他物体,无论其形状如何,只要保持固定不变,我们就可以得出结论:如果我们扩大比例,其体积将按照线性尺寸的立方倍数增长。
因此,当一个物体的边长增长时,它的体积的增速要远快于面积的增速。让我来举一个简单的例子:如果你把自己家房屋每条线的边长都增长一倍,它的形状不会发生变化,它的体积将增长至原来的2 3 =8倍,它的占地面积只会增长至原来的2 2 =4倍。举一个更加极端的例子,假设每条线都增长至原来的10倍,那么包括地面、墙面和天花板在内的所有平面的面积都将增长至原来的10×10=100倍,而房屋的体积则将增长至原来的10×10×10=1 000倍。
这对我们周围世界的设计和功能都将产生巨大的影响,无论是我们工作和生活于其中的建筑物,还是自然界中动物和植物的结构。例如,大多数暖气、冷气和光线都分别与暖气片、空调和窗户的表面积存在比例关系。因此,它们的效率增速将远远慢于需要加热、冷却或照明的生活空间的体积。当一座建筑扩大时,其体积也同样会不成比例地增长。同理,对大型动物而言,消耗掉通过新陈代谢和身体活动所产生的热量可能也会成为一个问题,因为与小型生物相比,消耗热量的身体表面积和体积之间的比例要小得多。例如,大象便进化出了面积不相称的庞大耳朵,通过增加身体表面积消散更多的热量,这才解决了这个挑战。
在伽利略之前的许多人可能都曾意识到面积和体积按比例缩放的根本不同。他所贡献出来的新洞见在于将这一几何学上的发现和他的发现结合在一起,即柱梁和肢干的强度是由它们的横截面面积决定的,而不是由它们的长度决定的。因此,假设一根柱子的矩形横截面面积为2英寸×4英寸(=8平方英寸),那么它便可以支撑4倍于横截面边长只有它一半的类似材料制成的柱子所能支撑的重量,而无论这些柱子有多长。第一根柱子可以是4英尺长,第二根柱子可以是7英尺长,这都没有关系。这就是参与建筑的建筑工人、建筑师、工程师都要根据横截面面积挑选木材的原因,也是家得宝和劳氏公司的木材区在展示木材时要注明“2×2、2×4、4×4”等尺寸的原因。
现在,当我们放大一栋建筑物或一只动物时,其重量也会随着体积的增长而相应增长,前提是其构成材质不能发生变化,以使密度保持一致。因此,体积增长一倍,重量便增长一倍。这样一来,一根柱子或一条腿所能够支撑的重量的增长幅度就要高过强度的增长幅度,因为重量(就像体积一样)的增长幅度是线性尺寸的立方倍数,而强度的增长幅度只是线性尺寸的平方倍数。为了强调这一点,假设一栋建筑物或一棵树的高度增长至原来的10倍,并保持形状不发生变化,那么需要被支撑的重量就将增长至原来的1 000(10 3 )倍,而支撑建筑物或树的柱子或树干的强度值增长至原来的100(10 2 )倍。因此,安全支撑额外重量的能力只有此前的1/10。由此一来,无论是什么组织或结构,如果它的规模尺寸任意增长,它的自身重量都终将会把它压垮。尺寸和增长都是有限度的。
换句话说,随着规模尺寸的增长,其相关强度会逐步变弱。或者,就像伽利略生动地表述的那样:“体形越小,其相对强度越大。因此,一只小狗能够背负两三只与自身同等大小的狗,但我相信,一匹马连一匹与自身同等大小的马都驮不了。”