下载掌阅APP，畅读海量书库
立即打开
研究函数就要了解函数的性质，下面介绍函数的几种特性。
设函数
y
=
f
（
x
），若存在正数
M
，使得在区间
D
上有
≤
M
，则称函数
f
（
x
）在
D
上
有界
。否则称函数
f
（
x
）在
D
上
无界
。
函数 y = f （ x ）在区间（ a ， b ）内有界的几何意义是：曲线 y = f （ x ）在（ a ， b ）区间内的图像被限制在 y = -M 和 y = M 两条直线之间，如图1-4所示。
图1-4
对于函数的有界性，要注意以下两点。
（1） 有界函数的界并不是唯一的。
例如，
f
（
x
）=sin
x
在（-∞，+∞）内是有界的，有
≤1，但我们也可以取
M
=2，即
＜2总是成立的。实际上
M
可以取任何大于1的数。
（2） 有界性是依赖于区间的。
例如，
在区间（0，1）是无界的，而在区间（1，2）内是有界的。
请思考： 我们以前学过那些有界函数？
例1.8
判断函数
的有界性。
解
因为1+
x
2
≥2
x
，
≤1故
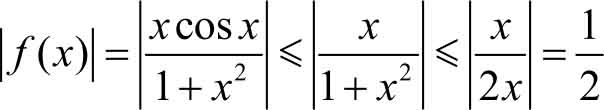
所以， f （ x ）是有界函数。
设函数 f （ x ）在 D 上有定义，如果对于属于 D 内任意两个点 x 1 ， x 2 ，当 x 1 ＜ x 2 时，都有 f （ x 1 ）＜ f （ x 2 ），则称函数 f （ x ）在 D 上是 单调增加 ；当 x 1 ＜ x 2 时，都有 f （ x 1 ）＞ f （ x 2 ），则称函数 f （ x ）在 D 上是 单调减少 。
单调增加函数与单调减少函数统称为 单调函数 。
单调增加函数的图像是沿 x 轴正方向逐渐上升的，如图 1-5 所示；单调减少函数的图像是沿 x 轴正方向逐渐下降的，如图1-6所示。
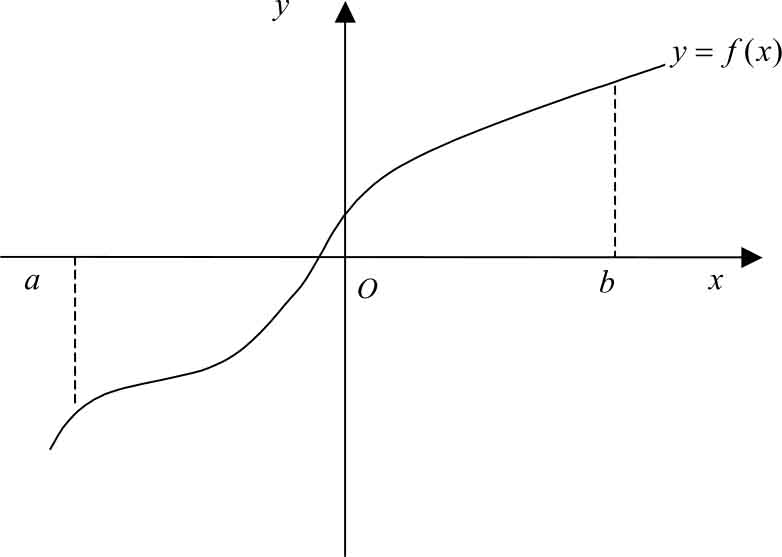
图1-5
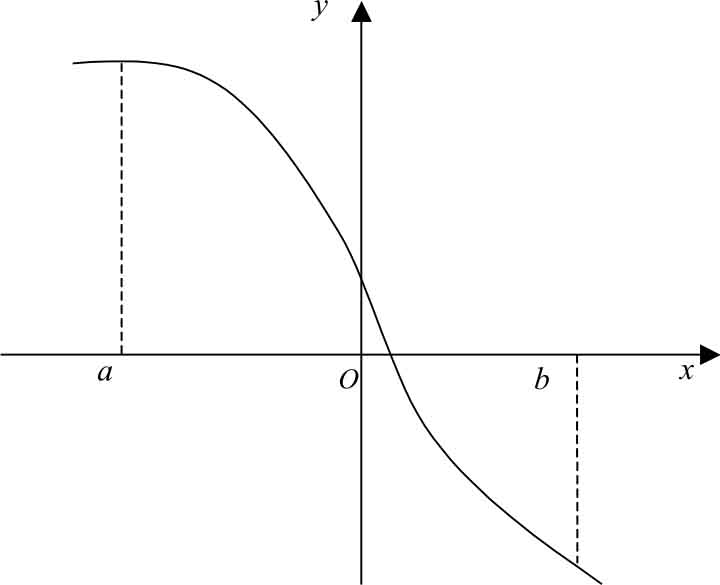
图1-6
例1.9 证明函数 f （ x ）=3 x +2在 R 上是增函数。
证 设 x 1 ， x 2 是 R 上的任意两个实数，且 x 1 ＜ x 2 ，则
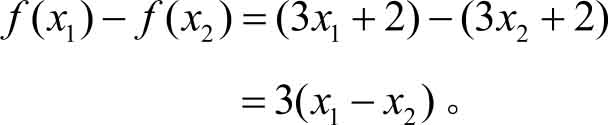
由 x 1 ＜ x 2 ，得 x 1 -x 2 ＜0，于是 f （ x 1 ） -f （ x 2 ）＜0，即 f （ x 1 ）＜ f （ x 2 ）。
所以，函数 f （ x ）=3 x +2在 R 上是增函数。证毕。
设 D 为关于原点对称的区间，若对于任意的自变量 x （ x ∈ D ），都有 f （ -x ）= f （ x ），则称 f （ x ）为 偶函数 ；若对于任意的自变量 x （ x ∈ D ），都有 f （ -x ）= -f （ x ），则称 f （ x ）为 奇函数 。
例如， y = x 2 在（-∞，+∞）内是偶函数，如图 1-7 所示； y = x 3 在（-∞，+∞）内是奇函数，如图1-8所示。
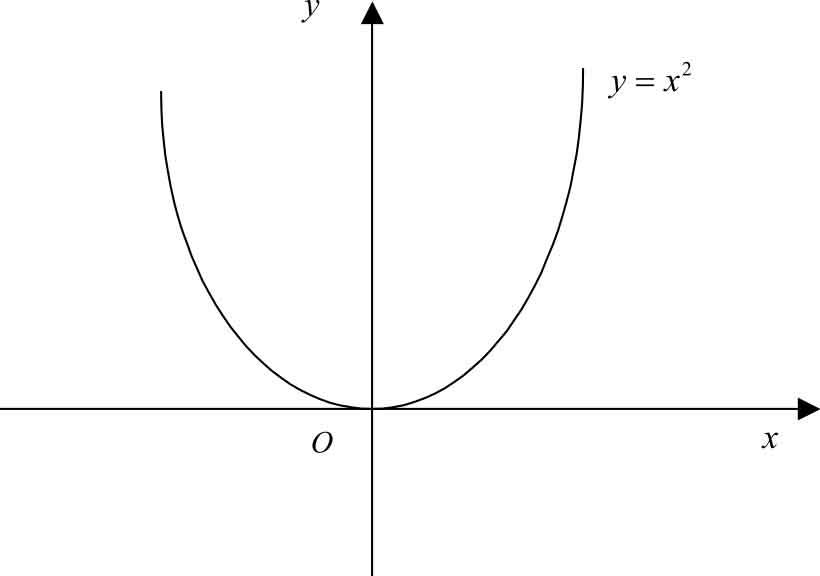
图1-7
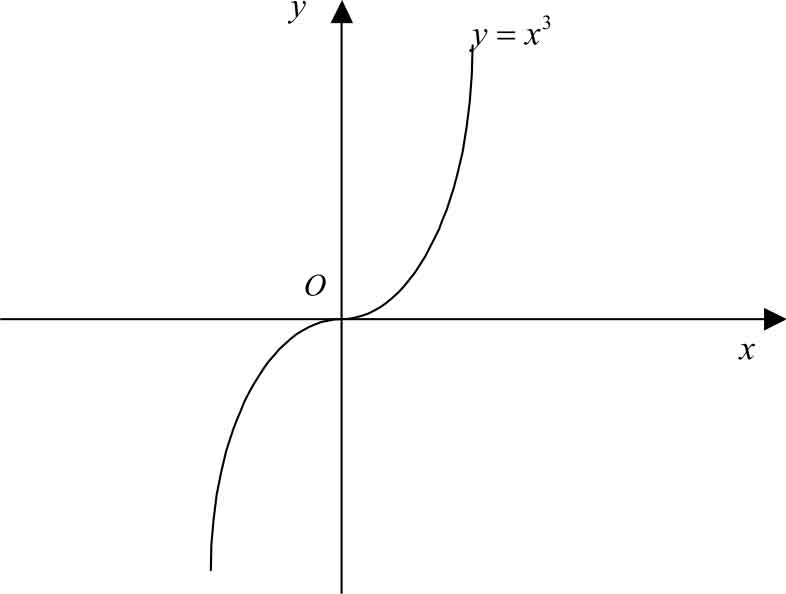
图1-8
从图1-7和图1-8可以看出，偶函数是关于 y 轴对称的；奇函数是关于坐标原点对称的。
例1.10 判断下列函数的奇偶性。
(1) f ( x )=3 x 4 -5 x 2 +7;
(2) f ( x )=2 x 2 +sin x ;
(3
a
＞0,
a
≠1).
解 由定义可知，三个函数的定义域都是（-∞，+∞），是关于原点为对称区间的。
（1）由于 f （ -x ）=3（ -x ） 4 -5（ -x ） 2 +7=3 x 4 -5 x 2 +7= f （ x ），所以， f （ x ）=3 x 4 -5 x 2 +7是偶函数。
（2） 由于 f （ -x ）=2（ -x ） 2 +sin（ -x ）=2 x 2 -sin x ≠ f （ x ），同样 f （ -x ）≠ -f （ x ），所以， f （ x ）=2 x 2 +sin x 是非奇非偶函数。
（3） 由于
，所以，
f
（
x
）=
为奇函数。
举例说明下列说法是否正确。
（1） 两个奇函数之和是奇函数；
（2） 两个偶函数之和是偶函数；
（3） 奇函数与偶函数之和是非奇非偶函数；
（4） 两个奇函数的乘积是偶函数；
（5） 两个偶函数的乘积是偶函数；
（6） 奇函数与偶函数的乘积是奇函数。
对于函数 y = f （ x ），如果存在正数 T ，使得对于任意 x ∈ D ，且 x + T ∈ D ，有 f （ x + T ）= f （ x ）恒成立，则称函数 f （ x ）为 周期函数 。满足这个等式的最小正数 T ，称为函数 f （ x ）的 周期 。例如 y =sin x 是周期函数，周期为2π。
请思考： 我们以前还学过那些周期函数？
判断下列函数的奇偶性。
1. f ( x )=e x -e -x ;
2. f ( x )= x 2 cos x ;
3.
f
(
x
)=
.