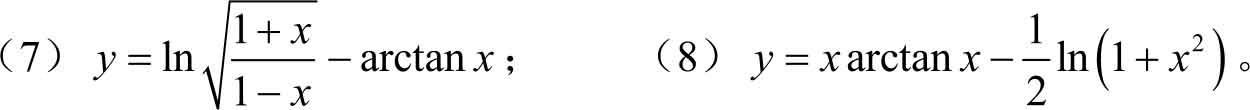3.3 复合函数的求导法则

到现在为止，我们只能求一些简单函数的导数，但在实际中遇到的函数大多是复合函数，下面介绍复合函数的求导法则。

法则4 设函数 y = f （ u ）在 u 点可导， u = φ （ x ）在 x 点可导，则复合函数 f [ φ （ x ）]在 x 点也可导，且

上述法则可以推广到有限个中间变量的情形。如 y = f （ u ）， u = φ （ t ）， t = s （ x ），则复合函数 y = f { φ [ s （ x ）]}的导数为

例3.20 求函数 y =e x 2 的导数。

解 设 y =e u ， u = x 2 ，

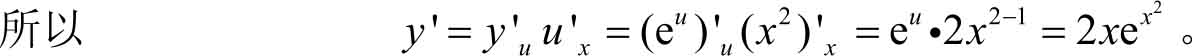
例3.21 设函数（1） y =sin 4 x ；（2） y =ln x 2 ；（3） y =log 2 cos x ；（4） 分别求出它们的导数 y ′。

解 （1）设 y = u 4 ， u =sin x ，则

（2）设 y =ln u ， u = x 2 ，则

（3）设 y =log 2 u ， u =cos x ，则

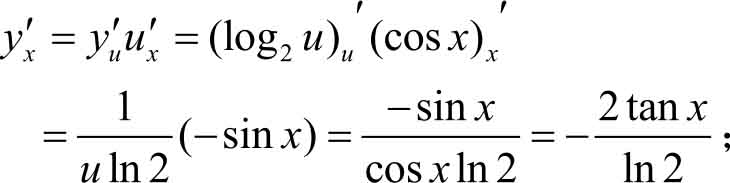
（4）设 y = ， u = a 2 -x 2 ，则

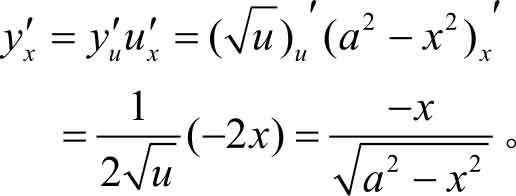
例3.22 求下列函数的导数。

(1) y =ln sin x 3 ;(2) y =ln cos 2 x .

解 （1）设 y =ln u ， u =sin v ， v = x 3 则

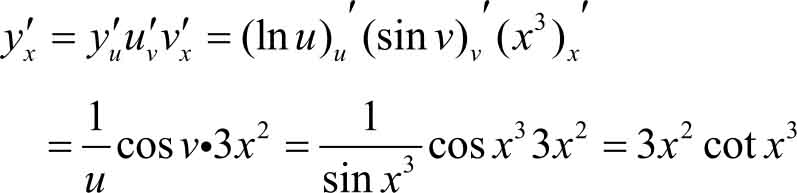
（2）设 y =ln u ， u =cos v ， v =2 x ，可得

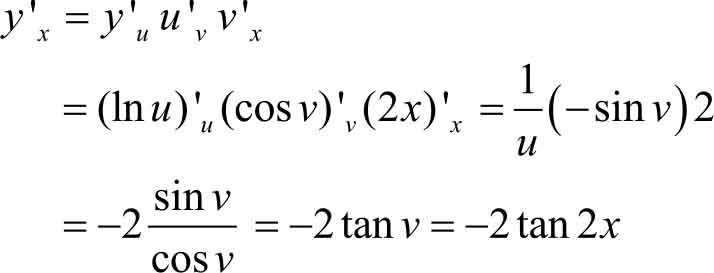
例3.23 求 的导数。

设 y = u -3 ， u =1-2 x ，则

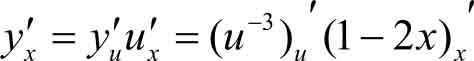
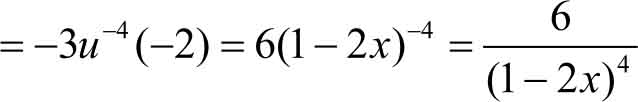
复合层次比较清楚以后，可不必设中间变量，直接由外往里，逐层求导，复合求导法则是相乘的关系。

例3.24 求函数 y =tan x 3 的导数。

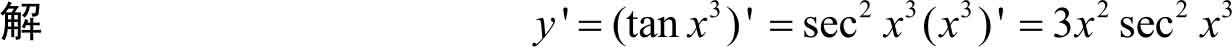
例3.25 设 y = 求 y ′。

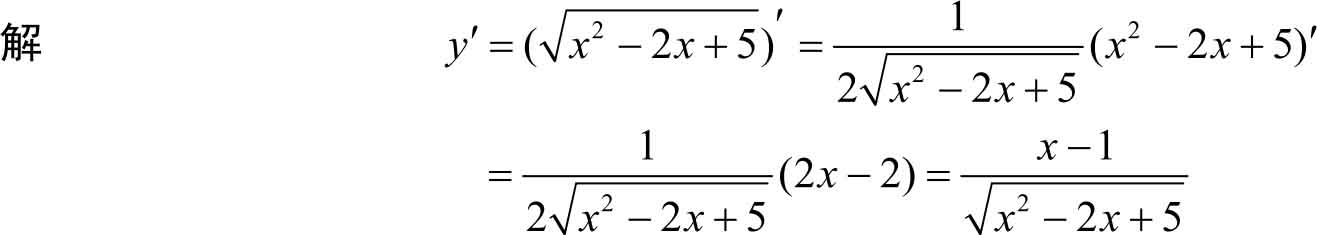
例3.26 设 ，求 y ′。

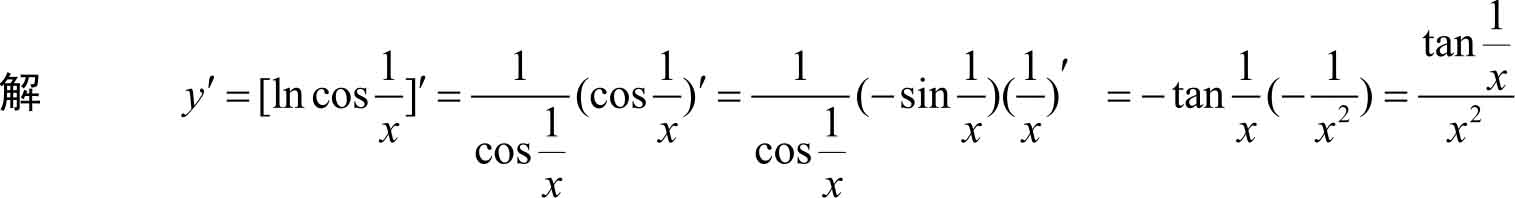
例3.27 求函数 的导数。

例3.28 求函数 y =sin 2 （cos3 x ）的导数。

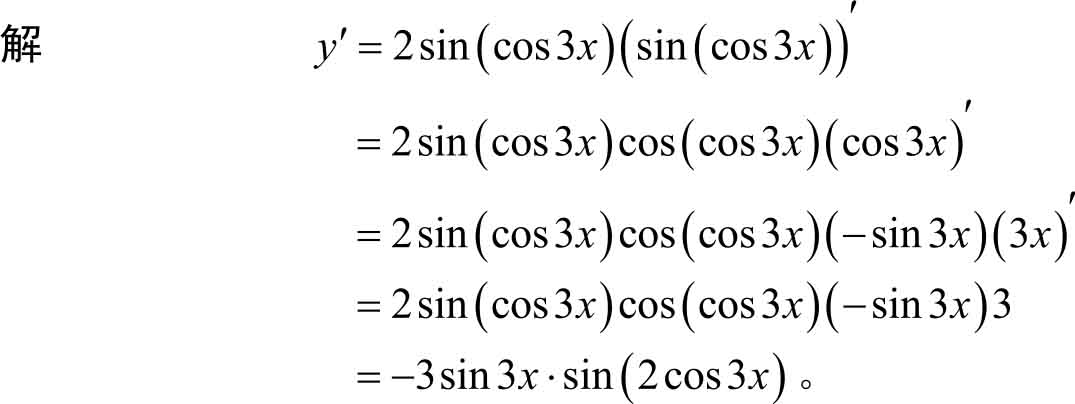
若函数有复合运算还有四则运算，那么求导时应遵循由外层向里，看见什么导什么，使用对应的法则。

例3.29 求函数 的导数。

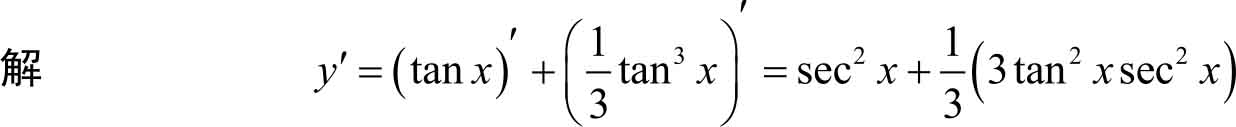
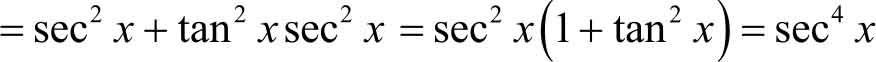
例3.30 求函数 y =sin n x sin nx 的导数。

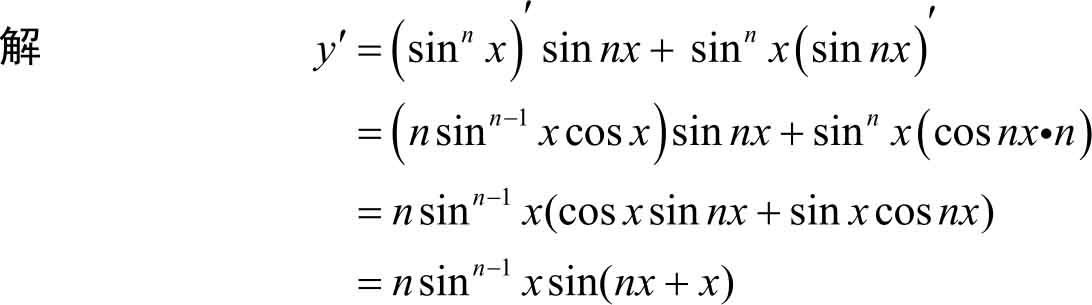
例3.31 求下列函数的导数。

分别求出它们的导数。

例3.32 （1）设 y = f （sin 2 x ）+ f （cos 2 x ），其中 f （ x ）可导，求 y ′；

（2）设 y = f （cos x ）， f ′（ x ）= ，求 ；

（3）设函数 f （ x ） 在（-∞，+∞）上可导，且 f （2）=4， f ′（2）=3， f ′（4）=5，求函数 y = f （ f （ x ））在点 x =2处的导数。

习题3.3

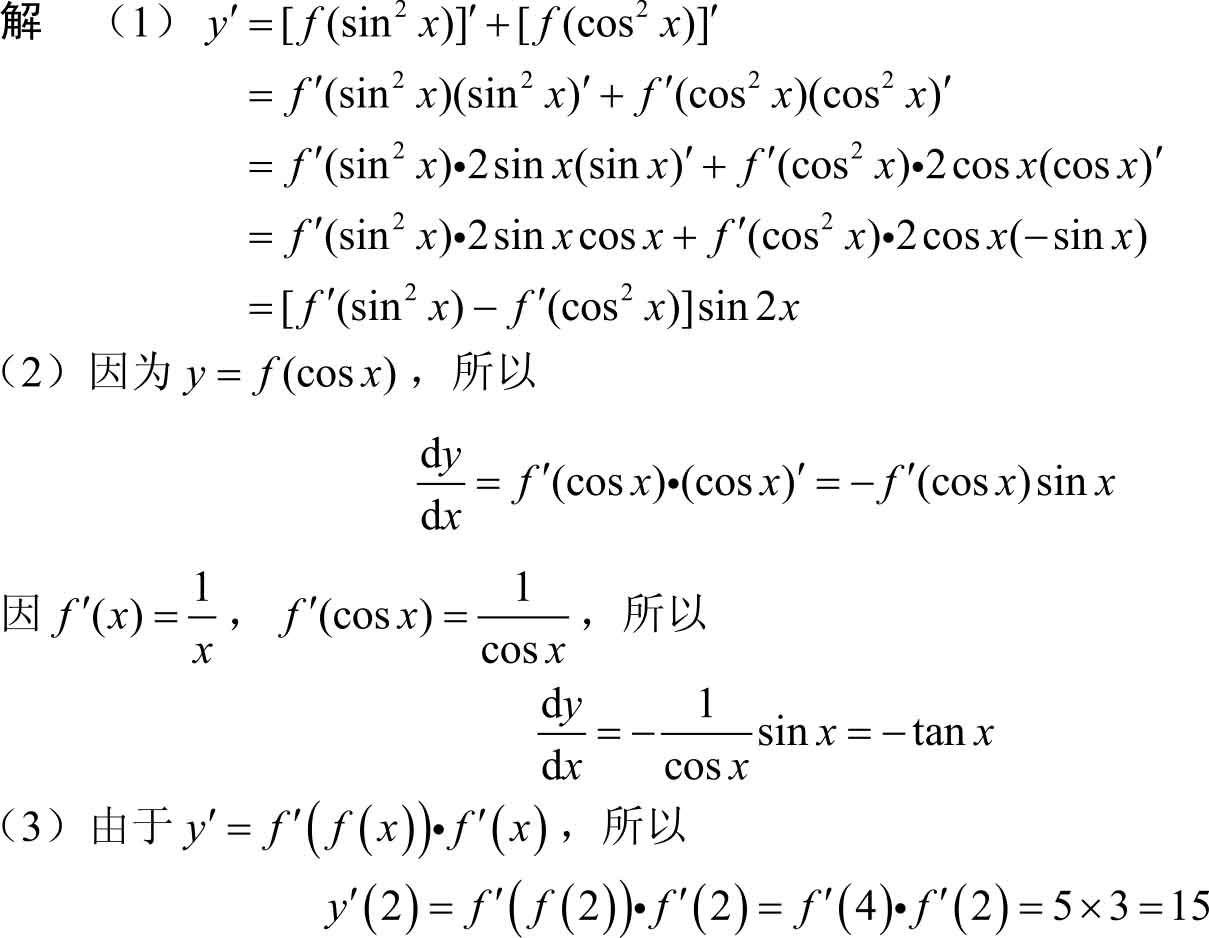
1.求下列函数的导数

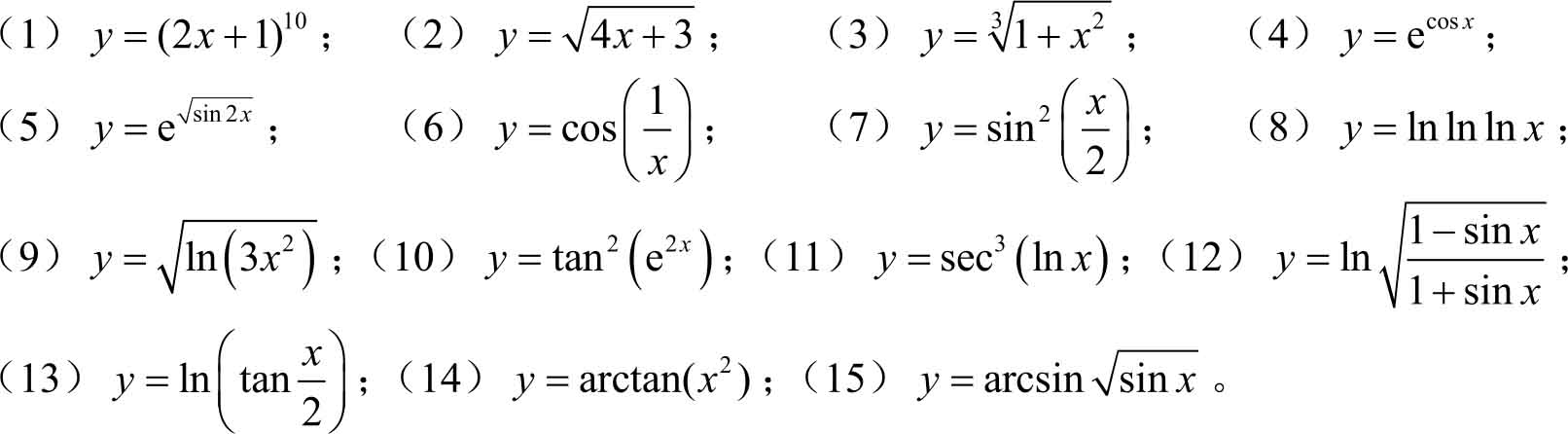
2.已知 f （ x ）= ，求 。

3.已知 y = f （sin x ）， f ′（ x ）=2 x ，求 。

4.求下列函数的导数。 RsiSUl3viOTU1xoeMuQlXYg6swKIE9HtGwJ3YmmzYH/9vPf+OtPK9TBZkC83iLsP