




由前一节的介绍可知,根据导数的定义可以求函数的导数。但是,如果对每一个函数都按导数的定义来求导,其计算将会比较复杂,甚至比较困难。因此,有必要找到一些基本公式与运算法则,借助它们简化初等函数求导计算。
为了运算方便,下面先给出基本初等函数的导数公式,见表3-1所列。这些公式有的在3.1中已经得到,有的将随着导数运算法则的引入而得到,有的可参阅相关教材。
表3-1

例3.9
设函数(1)
y
=
x
10
,(2)
y
=
 ,(3)
,(3)
 ,(4)
y
=log
3
x
,(5)
y
=ln 3,分别求出它们的导数
y
′。
,(4)
y
=log
3
x
,(5)
y
=ln 3,分别求出它们的导数
y
′。
解 由导数公式得

例3.10
(1)设
y
=
 ,求
,求
 ;(2)设
y
=log
3
x
,求(log
3
x
)′|
x
=3
;(2)设
y
=log
3
x
,求(log
3
x
)′|
x
=3
解
(1) 由于
 ,所以
,所以
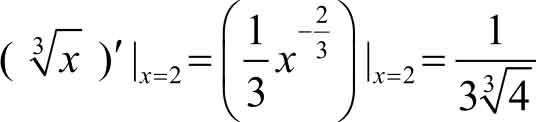
(2) 由于
 ,所以
,所以
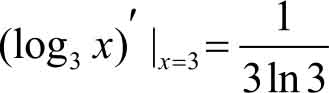
设函数 u = u ( x )和 v = v ( x )在 x 处可导,则其和、差、积、商在 x 处也可导。
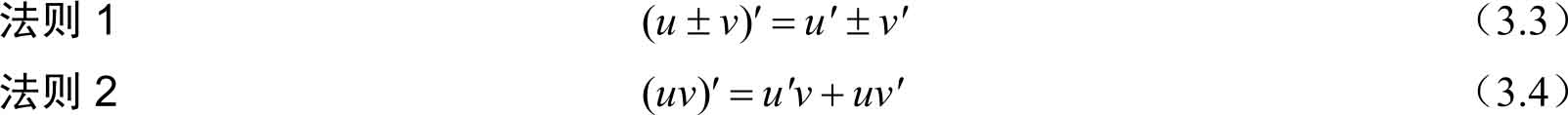
特别地,( Cu ) ′ = Cu′ ( C 为常数)
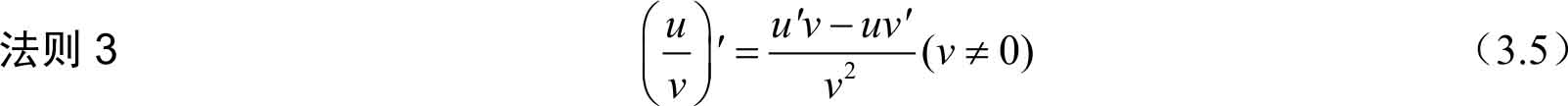
特别地,
 (
v
≠0,
C
为常数)
(
v
≠0,
C
为常数)
例3.11 求函数 f ( x )= x 3 +sin x 的导数。
解 f′ ( x )=( x 3 ) ′ +(sin x ) ′ =3 x 3-1 +cos x =3 x 2 +cos x 。
例3.12 求函数 f ( x )=e x cos x 的导数。
解 f′ ( x )=(e x ) ′ cos x +e x (cos x ) ′ =e x cos x -e x sin x 。
例3.13
求函数
 的导数。
的导数。
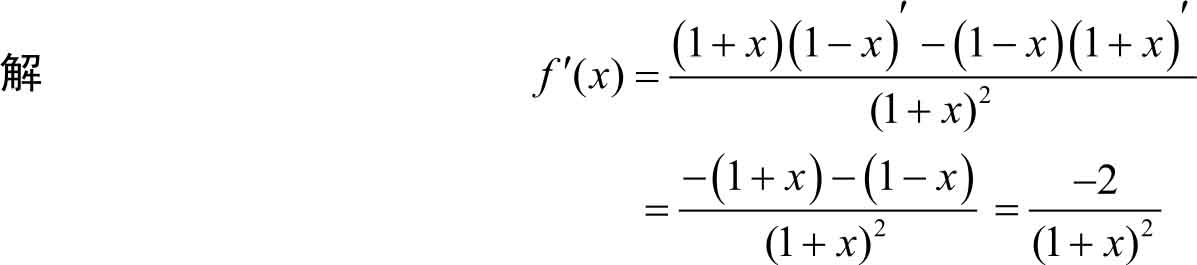
例3.14 求函数 f ( x )=tan x 的导数。
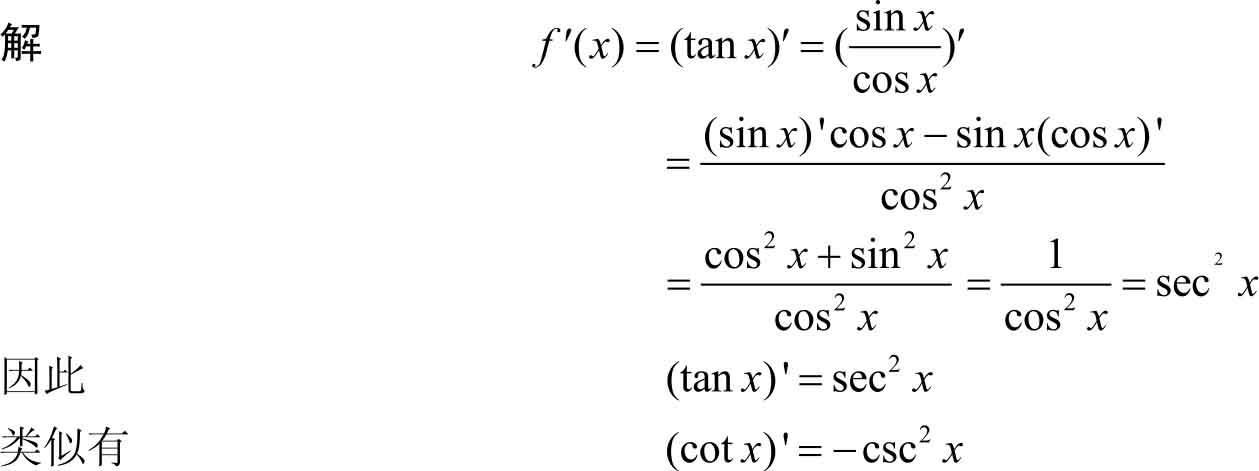
例3.15 求函数 f ( x )=sec x 的导数。
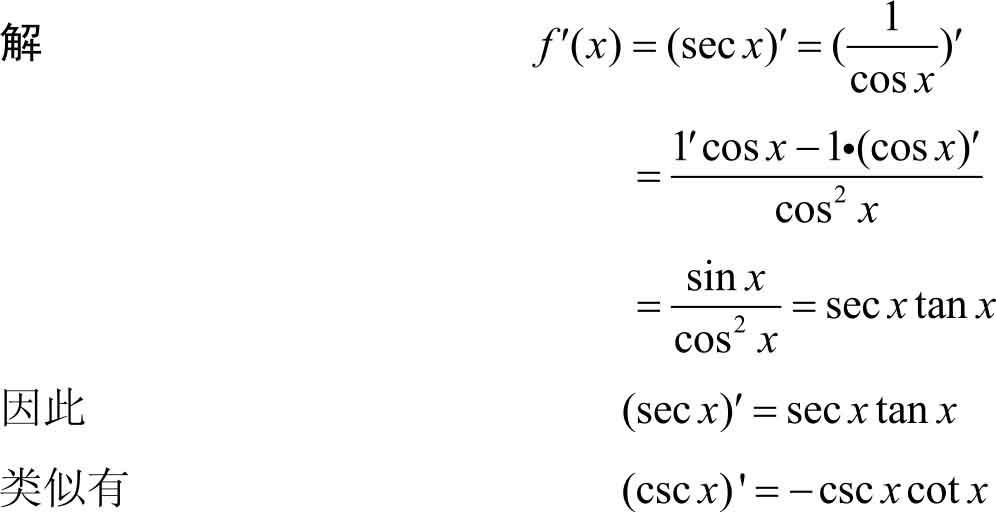
例3.16 求曲线 y = x ln x 的平行于直线2 x-y +3=0的切线方程。
解 本题切线的斜率间接给出,只要求出切点即可。
设所求切线的切点为( x 0 , y 0 ),因曲线为 y = x ln x ,所以
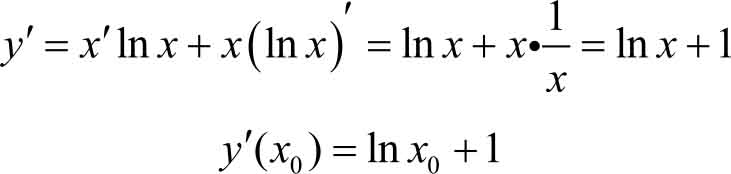
又因直线 2 x-y +3=0的斜率为2,且其与所求切线平行,因此可知所求切线的斜率也为2,故

函数
y
=
f
(
x
)的导数
f′
(
x
)一般也是
x
的函数,对
f′
(
x
)的再求导数,称为
f
(
x
)的
二阶导数
,记作
f
′′(
x
),
y
′′;或
 。
。
类似地,我们还可以继续求导,得到三阶导数 y ′′′,四阶导数 y (4) ,乃至 n 阶导数 y ( n ) 。二阶及二阶以上的导数统称 高阶导数 ,而 f′ ( x )称为 y = f ( x )的一阶导数。
由此可知,求高阶导数只要反复应用求一阶导数的方法即可,下面举例说明。
例3.17 已知 y = x 3 +ln x ,求 y ′, y ′′及 y ′′′。

例3.18 求 y = x arctan x 的二阶导数 y ′′
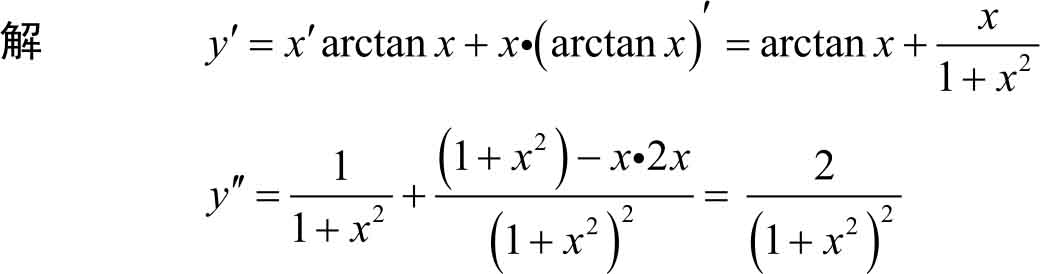
例3.19
设
 。
。

1.求下列函数的导数
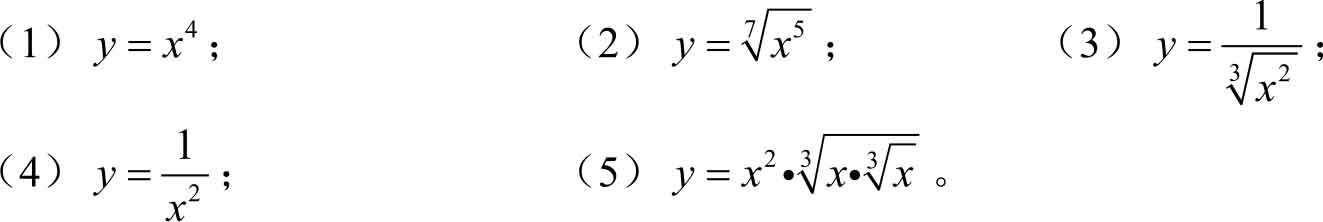
2.求下列函数的导数
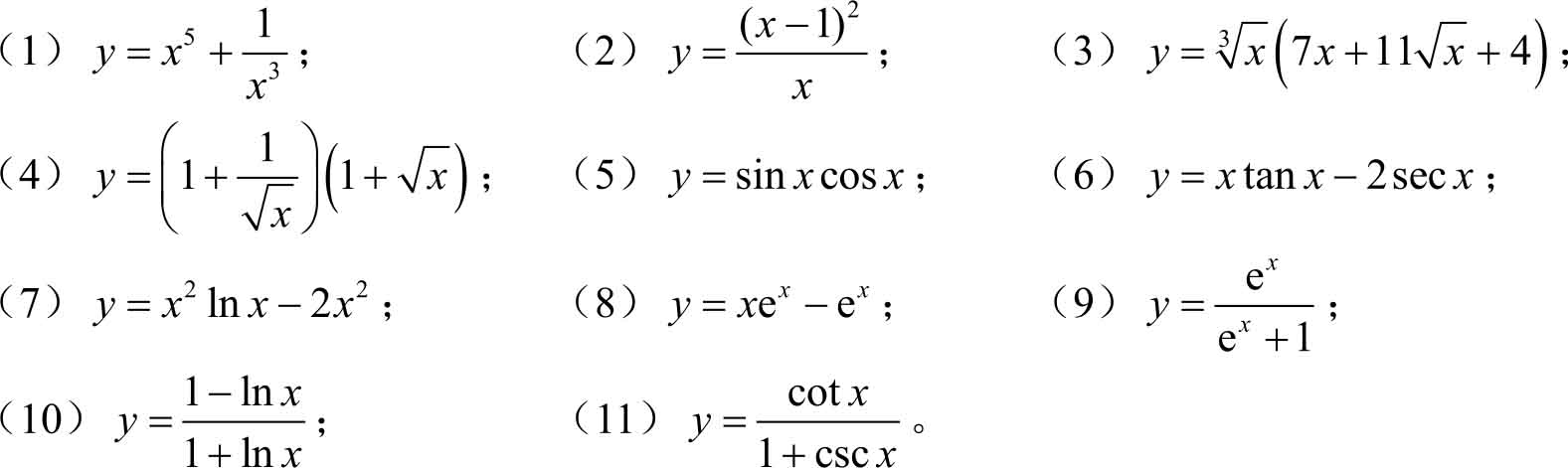
3.设
 ,求
f
′(4)。
,求
f
′(4)。
4.设
 ,求
f
′(e)。
,求
f
′(e)。
5.求 f ( x )= x 3 +2 x 2 在 x =1处的切线及法线方程。
6.曲线
y
=
 上哪一点的切线垂直于直线3
x
+
y
+1=0?
上哪一点的切线垂直于直线3
x
+
y
+1=0?
7.已知物体的运动规律为 s =2 t 2 + t (m),求这物体在 t =2(s)时的速度。
8.求下列函数的二阶导数
(1) y = x 3 +3 x 2 +2;(2) y = x ·sin x +cos x ;(3) y = x 2 +2 x +ln 2;(4) y = x e x .