




导数的概念来自于对实际问题的分析和研究。
设一物体做直线运动,从某一时刻开始到时刻 t 所经过的位移为 s ,则 s 是时刻 t 的函数 s = s ( t )。现在来确定物体在某一给定时刻 t 0 的速度。
当时间由 t 0 改变到 t 0 +Δ t 时,物体在Δ t 这段时间内所经过的位移为
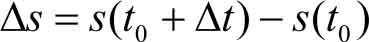
因此在Δ t 这段时间内,物体的平均速度为
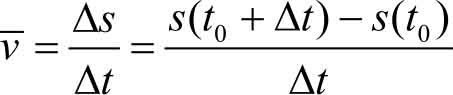
若物体做匀速运动,平均速度
 就是物体在任何时刻的速度
v
。若物体的运动是变速的,则当Δ
t
很小时,
就是物体在任何时刻的速度
v
。若物体的运动是变速的,则当Δ
t
很小时,
 可以近似地表示物体在
t
0
时刻的速度,Δ
t
越小,近似程度越好。当Δ
t
→0时,如果极限
可以近似地表示物体在
t
0
时刻的速度,Δ
t
越小,近似程度越好。当Δ
t
→0时,如果极限
 存在,则此极限为物体在
t
0
时刻的瞬时速度,即
存在,则此极限为物体在
t
0
时刻的瞬时速度,即
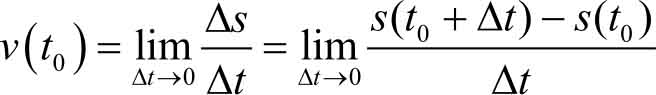
什么样的直线是曲线在某点处的切线呢?
设曲线 y = f ( x )的图像如图3-1所示,点 M 0 ( x 0 , y 0 )是曲线的一个定点,在曲线上另取一动点 M ( x 0 +Δ x , y 0 +Δ y ),作割线 M 0 M ,让点 M 沿曲线向 M 0 移动,则割线 M 0 M 的位置也随之变动,当点 M 沿曲线趋向 M 0 时,割线 M 0 M 趋向于极限位置 ——M 0 T ,则直线 M 0 T 就是曲线在 M 0 点处的切线。
从图3-1中可以看出, M 0 M 的斜率为
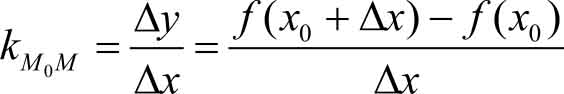

图3-1
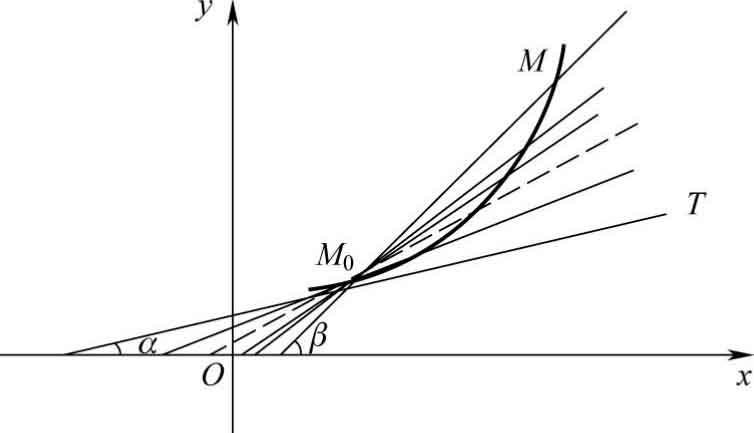
图3-2
当Δ x →0时,割线的斜率就无限地接近于切线的斜率,所以切线的斜率为
图3-2显示了割线到切线的变化过程。
上面两个例题虽然含义不同,但从抽象的数量关系来看,它们的实质是一样的,都归结为计算函数改变量与自变量改变量的比,当自变量的改变量趋于零时的极限,这种特殊的极限就称为函数的导数。
定义 3.1
设函数
y
=
f
(
x
)在点
x
0
的某个邻域内有定义,当自变量在点
x
0
处取得改变量Δ
x
时,函数
f
(
x
)取得相应的改变量Δ
y
=
f
(
x
0
+Δ
x
)
-f
(
x
0
),如果极限
 存在,则称这个极限值为
f
(
x
)在点
x
0
处的
导数
。记作
存在,则称这个极限值为
f
(
x
)在点
x
0
处的
导数
。记作
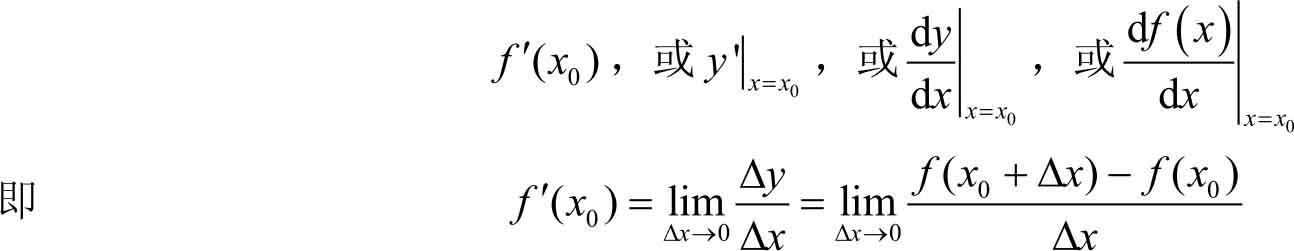
并称函数在点 x 0 处可导。
与函数
y
=
f
(
x
)在点
x
0
处的左、右极限概念相似,如果
 存在,则分别称这两个极限为
f
(
x
)在点
x
0
处的
左导数
和
右导数
,分别记作
存在,则分别称这两个极限为
f
(
x
)在点
x
0
处的
左导数
和
右导数
,分别记作
 。
。
显然,函数 y = f ( x )在点 x 0 处可导的充要条件是:函数 y = f ( x )该点处的左导数与右导数均存在且相等。
如果上述极限不存在,则称 f ( x )在点 x 0 处不可导。如果极限为无穷大,为方便起见,也称函数在点 x 0 处的导数为无穷大。
如果函数
f
(
x
)在某区间(
a
,
b
)内的每一点都可导,则称
f
(
x
)在区间(
a
,
b
)内可导,这时,对于(
a
,
b
)内的每一点
x
,都有确定的导数值与它对应,这样就构成了一个新的函数,称为函数
f
(
x
)的
导函数
,记作
f
′(
x
)或
y′
,
 。在不致发生混淆的情况下,导函数也简称导数。
。在不致发生混淆的情况下,导函数也简称导数。
有了导数的定义,前面的两个例题就可以如下叙述。
(1) 位移 s 对时间 t 的导数为瞬时速度 v ,即
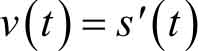
(2) 函数 f ( x )在 x 处的导数为曲线 f ( x )在 x 处的切线的斜率,即
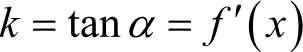
根据导数的定义,求导数有三个步骤:
(1) 求Δ y ;
(2) 求
 ;
;
(3) 求
 。
。
例3.1 求函数 f ( x )= C ( C 是常数)的导数。
解 (1) Δ y = f ( x +Δ x ) -f ( x )= C-C =0;
(2

(3

即 C ′=0
推导的结果告诉我们,常数的导数等于零。
例3.2 求函数 f ( x )= x n ( n ∈ N )的导数。
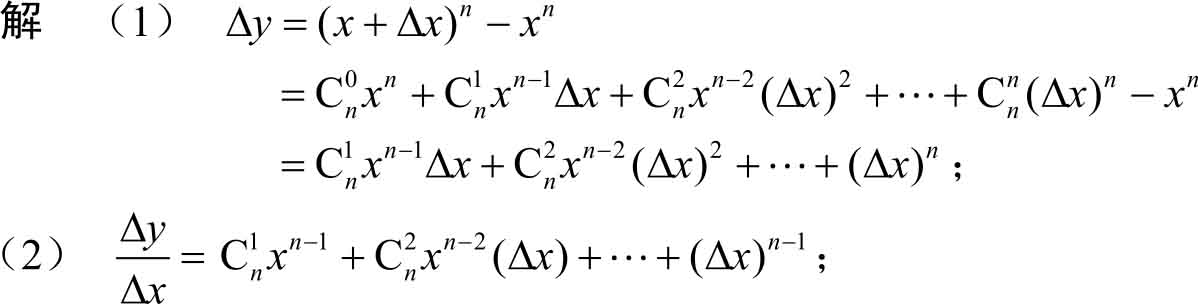
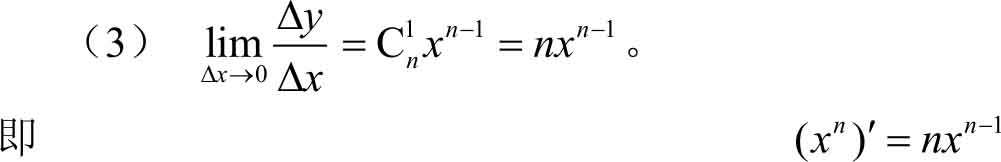
对于一般的幂函数 y = x α (α为实数)上面的公式也成立,即( x α )′=α x α -1 。
例3.3 求函数 f ( x )=sin x 的导数。
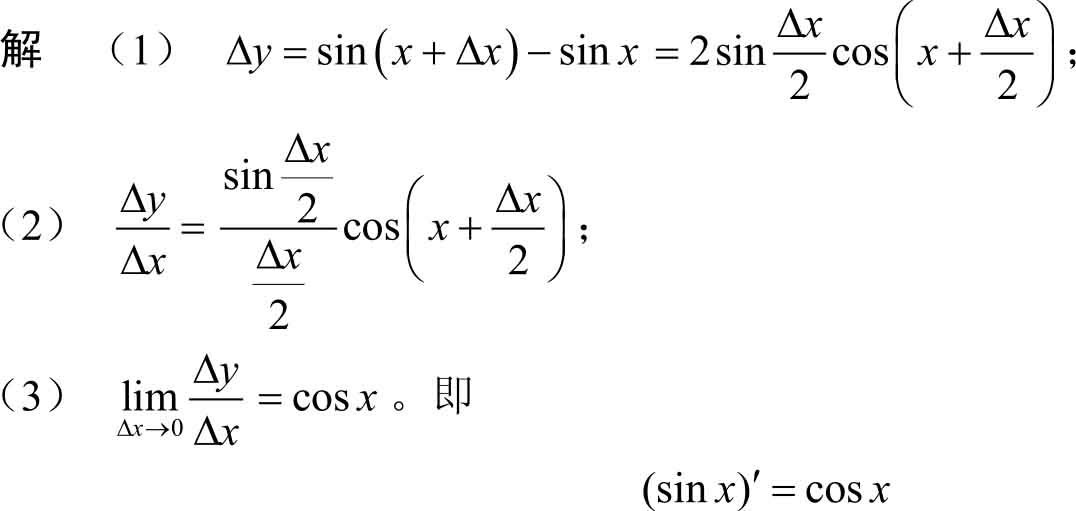
推导的结果告诉我们,正弦函数的导数恰好是余弦函数。类似可推导余弦函数的导数是负的正弦函数,即(cos x )′=-sin x 。
例3.4 求函数 f ( x )=log a x ( a >0, a ≠1)的导数。
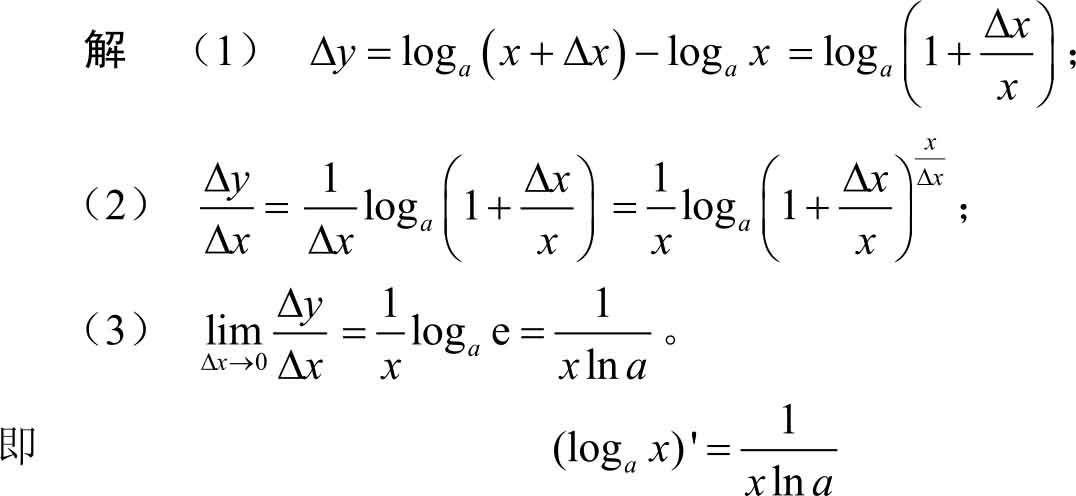
函数在某点的导数的几何意义是曲线上该点处的切线的斜率,于是有以下结论。
(1) 若曲线 f ( x )在 x 0 处可导,则曲线在点( x 0 , y 0 )处的切线方程为

特别地,如果
f
′(
x
0
)=tan
α
=∞,则
 ,即切线垂直于
x
轴,切线方程为
x
=
x
0
。
,即切线垂直于
x
轴,切线方程为
x
=
x
0
。
(2) 若曲线 f ( x )在 x 0 处可导,则曲线在点( x 0 , y 0 )处的法线方程为

例3.5 求曲线 f ( x )= x 3 当 x =1时对应点的切线方程。
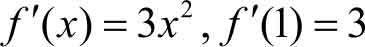
设切线的斜率为 k ,切点处的导数就等于切线的斜率,得
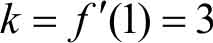
所以切线方程为 y -1=3 ( x -1)
即
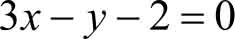
例3.6 求曲线 f ( x )=ln x 在点(e,1)处的切线方程。

切线方程为
 。
。
定理3.1 如果函数 f ( x )在 x 0 处可导,则它在 x 0 处一定连续。
这个定理的逆定理不成立,即如果函数 f ( x )在 x 0 处连续,则函数 f ( x )在 x 0 处未必可导。
例3.7
设
f
(
x
)=
 ,问
f
(
x
)在
x
=0处是否可导?
,问
f
(
x
)在
x
=0处是否可导?
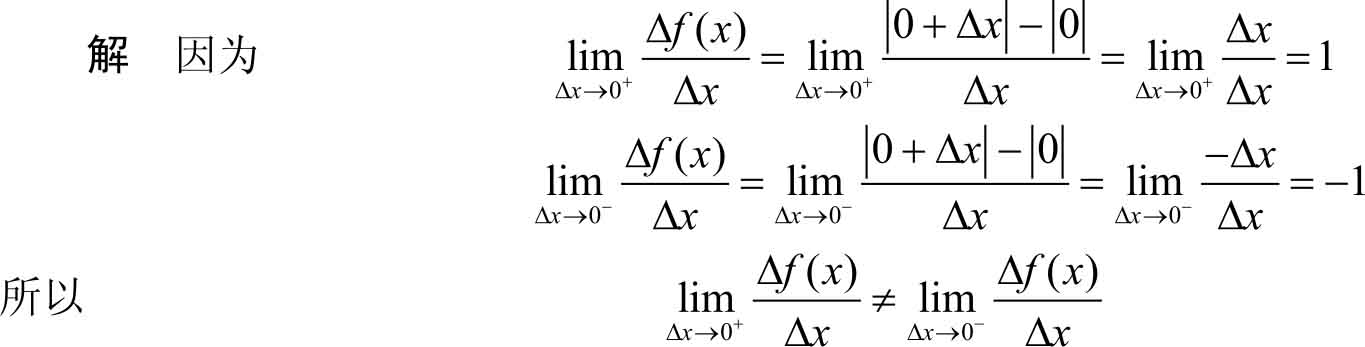
故
 不存在,即
f
(
x
)在
x
=0处不可导,在图3-3上表现为曲线
f
(
x
)=
不存在,即
f
(
x
)在
x
=0处不可导,在图3-3上表现为曲线
f
(
x
)=
 在点
x
=0处有一个“尖点”,没有切线。
在点
x
=0处有一个“尖点”,没有切线。

图3-3
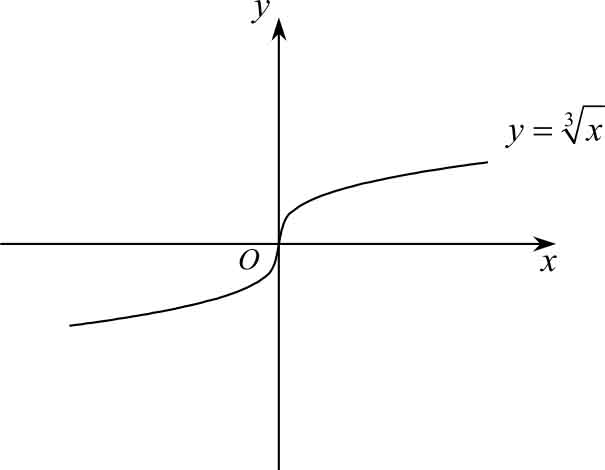
图3-4
例3.8
设
f
(
x
)=
 ,问
f
(
x
)在
x
=0处是否可导?
,问
f
(
x
)在
x
=0处是否可导?
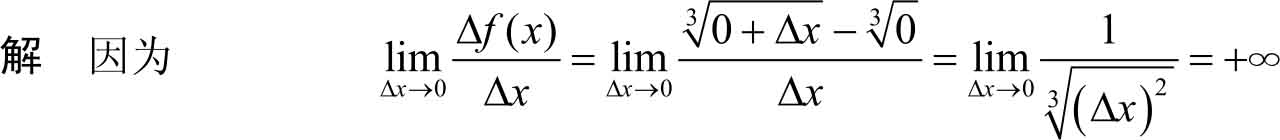
即
f
(
x
)在
x
=0处不可导,在图3-4上表现为曲线
f
(
x
)=
 在点
x
=0处有垂直于
x
轴的切线。
在点
x
=0处有垂直于
x
轴的切线。
以上两例所给曲线在点 x =0处都不可导,但很容易判断所给曲线在点 x =0处都是连续的。
1.下列各题中均假定 f ′( x 0 )存在,按照导数定义观察下列极限,指出 A 表示什么?
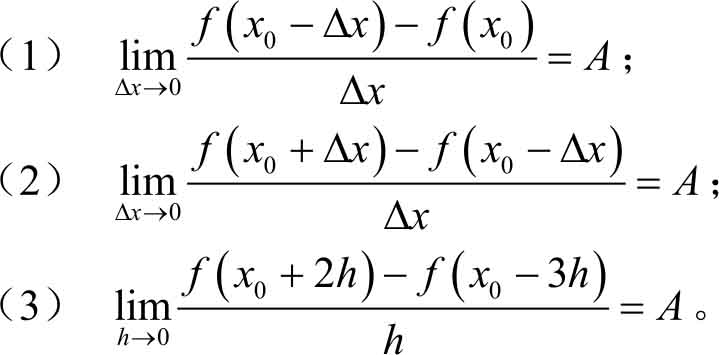
2.设 f ( x )=cos x ,试按导数定义求 f ′( x )。