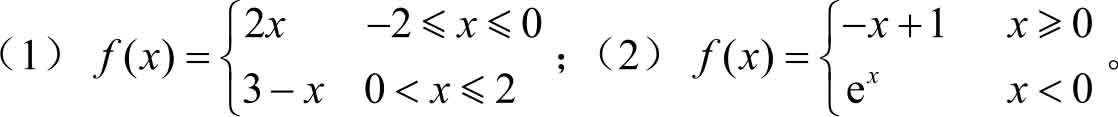数列 是指对自变量为正整数的函数 u n = f ( n ) ( n =1,2,3,…)的函数值按自变量 n 由小到大的顺序排列成一列数:
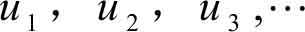
记作 { u n }。其中 u n 为数列 { u n }的通项或一般项。由于一个数列 { u n }完全由一般项 u n 所确定,故经常把数列 { u n }简称为数列 u n 。如果数列 u n = f ( n )中的 n →∞时,我们称之为无穷数列;如果数列 u n = f ( n )中的 n 只是一个具体数值,我们称之为有穷数列。
现在观察几个无穷数列 u n = f ( n ),并判定它们当自变量 n 无限增大时的变化趋势。
(1) 数列
 ,…
,…
当自变量
n
无限增大时,
 的值越来越小(单调下降)无限接近于常数0。
的值越来越小(单调下降)无限接近于常数0。
(2) 数列
 ,…
,…
当自变量
n
无限增大时,
 的值越来越大(单调上升)无限接近于常数1。
的值越来越大(单调上升)无限接近于常数1。
(3) 数列
 ,…
,…
当自变量
n
无限增大时,
 的值随着
n
的增大从0的两侧无限接近于常数0。
的值随着
n
的增大从0的两侧无限接近于常数0。
可以看出,当自变量 n 无限增大时,上述的三个数列所具有的共同特征是 u n 的值都会趋向于某个常数 A 。
(4) 数列{(-1) n +1 n }:1,-2,3,-4,…,(-1) n +1 n ,…
当自变量 n 无限增大时, u n =(-1) n +1 n 的值的绝对值是无限增大的。
(5) 数列{(-1) n +1 }:1,-1,1,-1,…,(-1) n +1 ,…
当自变量 n 无限增大时, u n =(-1) n +1 的值在1和-1之间跳动,没有固定的变化趋势。
可以看出,当自变量 n 无限增大时,上述两个数列不会趋向于某个常数 A 。
定义2.1 对于数列 { u n },如果当 n 无限增大时, u n 趋向于某个常数 A ,则称当 n 趋于无穷大时,数列 { u n }以 A 为极限。记作
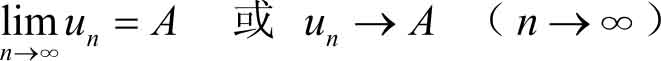
也称数列 { u n } 收敛于 A 。如果数列 { u n }没有极限,就称数列 { u n }是 发散的 。
 这个式子读作“当
n
趋向于无穷大时,
u
n
的极限等于
A
”。符号“→”表示“趋向于”,“
n
→∞”表示“
n
趋向于无穷大”,就是
n
无限增大的意思。
这个式子读作“当
n
趋向于无穷大时,
u
n
的极限等于
A
”。符号“→”表示“趋向于”,“
n
→∞”表示“
n
趋向于无穷大”,就是
n
无限增大的意思。
例2.1 观察下列数列的变化趋势,写出它们的极限。
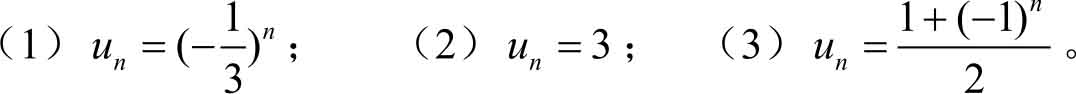
解 (1)当 n 依次取1,2,3,4,…时,数列的各项顺序为

当
n
→∞时,
 正负交错,但其绝对值越来越小趋向于 0,即
u
n
→0。故
正负交错,但其绝对值越来越小趋向于 0,即
u
n
→0。故
 =0。
=0。
(2)当 n 依次取1,2,3,4,…时,数列的各项顺序为
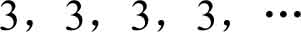
当
n
→∞时,
u
n
=3的值永远都是常数3,即
u
n
=3。故
 =3。
=3。
一般地,任何一个常数列的极限都是这个常数本身,即
 =
C
(
C
为常数)。
=
C
(
C
为常数)。
(3)当 n 依次取1,2,3,4,…时,数列的各项顺序为
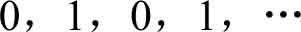
当
n
→∞时,
 的值在0,1,0,1点来回摆动,不趋向于某个固定的常数,此时我们说
的值在0,1,0,1点来回摆动,不趋向于某个固定的常数,此时我们说
 不存在。
不存在。
定理2.1 (单调有界原理) 单调有界数列必有极限。
通过上面我们对数列极限的介绍,对“极限”的概念已有了足够的认识,即已知函数 f ( x ),当 x 取自然数时,得数列 u n = f ( n )。讨论数列 u n = f ( n )的极限就是研究当 n 越来越大时, f ( n )变化趋势如何?在此,我们在数列极限的基础上进一步研究函数 f ( x )的极限问题,也就是探讨当 x 在某一变化过程中,函数 f ( x )是如何变化的?
考察函数
 ,当
x
→∞时的变化趋势。由图2-2可以看出,当自变量
x
取正值并无限增大(即
x
趋向于正无穷大)时,函数
,当
x
→∞时的变化趋势。由图2-2可以看出,当自变量
x
取正值并无限增大(即
x
趋向于正无穷大)时,函数
 的值无限接近于 0。根据这种变化趋势,我们说当
x
趋向于正无穷大时,函数
的值无限接近于 0。根据这种变化趋势,我们说当
x
趋向于正无穷大时,函数
 的极限为 0,记作
的极限为 0,记作
 。
。
同样地,当自变量
x
取负值并且它的绝对值无限增大(即
x
趋向于负无穷大)时,函数
 的值也无限接近于 0。于是我们说,当
x
趋向于负无穷大时,函数
的值也无限接近于 0。于是我们说,当
x
趋向于负无穷大时,函数
 的极限为0。记作
的极限为0。记作
 。
。

图2-2
由此可以看出,当
x
→∞(它包含
x
→+∞和
x
→-∞两种情况)时,函数
 。
。
定义2.2 设函数 f ( x )对于任意大的 x 有定义,如果当 x 的绝对值无限增大(即 x →∞)时,函数 f ( x )无限的趋近于一个确定的常数 A 。那么则称当 x →∞时,函数 f ( x )以 A 为极限。记作
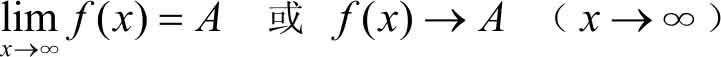
在定义中,如果只考虑 x →+∞的情形,就记作
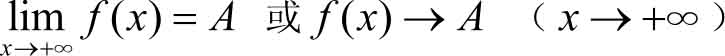
如果只考虑 x →-∞的情形,就记作

显然,
 。
。
例2.2
求
 。
。
解
分析函数2
x
,当
x
→-∞时,其值越来越小趋向于 0,如图 2-3 所示,可得
 =。
=。
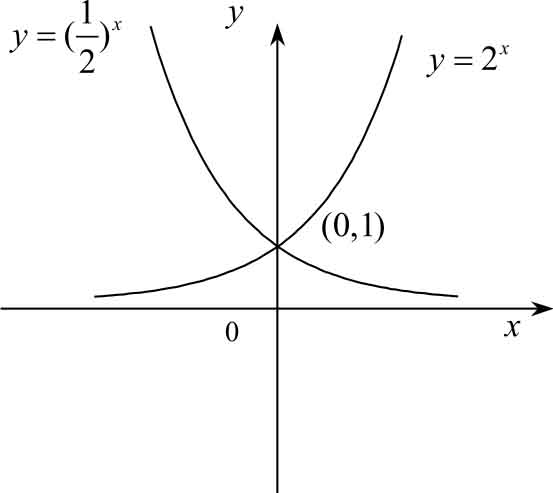
图2-3
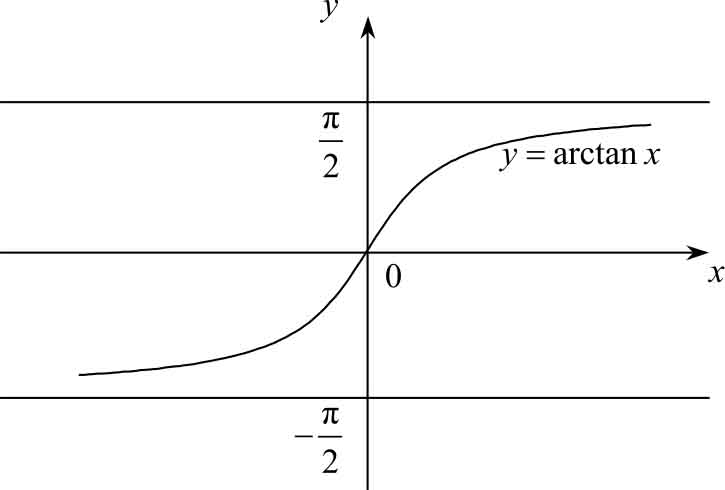
图2-4
例2.3 讨论当 x →∞时,函数 y =arctan x 的极限。
解
观察图2-4所示可得:
 。
。
由于
 不存在。
不存在。
为了便于理解
x
→
x
0
时,函数
f
(
x
)极限的定义,我们先从图2-5和图2-6中观察两个具体的函数,
f
(
x
)=
x
+1和
 。
。
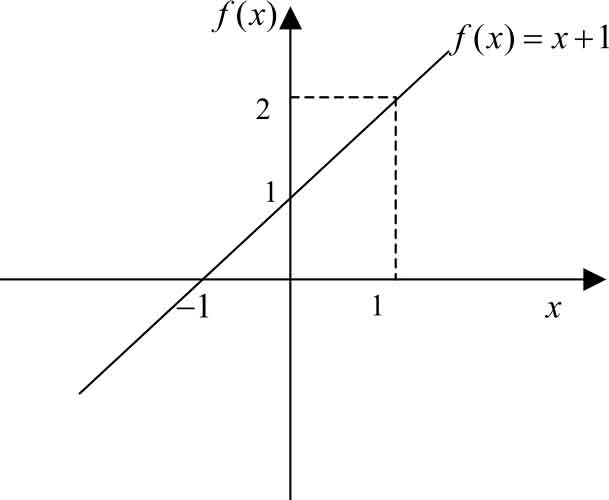
图2-5
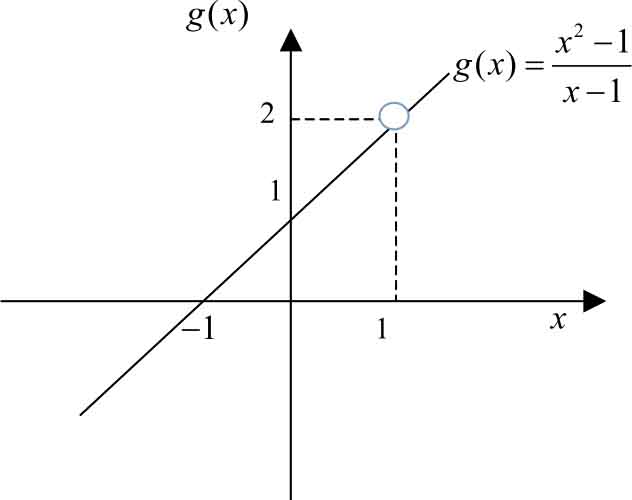
图2-6
不难看出,当
x
→1时,无论
x
在1左或右的那侧靠近1,
f
(
x
)和
g
(
x
)都无限接近于2。要特别注意函数
f
(
x
)=
x
+1与
g
(
x
)=
 是两个不同的函数,
f
(
x
)在
x
=1处有定义,
g
(
x
)在
x
=1处没有定义。这就是说,当
x
→1时,
f
(
x
)和
g
(
x
)的极限是否存在与其在
x
=1处是否有定义无关。
是两个不同的函数,
f
(
x
)在
x
=1处有定义,
g
(
x
)在
x
=1处没有定义。这就是说,当
x
→1时,
f
(
x
)和
g
(
x
)的极限是否存在与其在
x
=1处是否有定义无关。
定义 2.3 设函数 y = f ( x )在点 x 0 的某个空心邻域(点 x 0 本身可以除外)内有定义,当自变量 x 在该邻域内无限接近于点 x 0 时,相应的函数 f ( x )无限趋近于某个常数 A ,则称当 x 趋于 x 0 时,函数 f ( x )以 A 为极限。记作
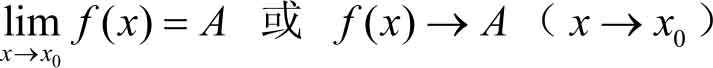
由定义2.3 可见,l
x
i
→1
m(
x
+1)=2,
 。
。
根据极限定义,我们可以看到
:
 (
C
为常数)。
(
C
为常数)。
定义 2.4 设函数 y = f ( x )在点 x 0 左侧的某个邻域(点 x 0 本身可以除外)内有定义,当自变量 x ( x < x 0 )在该邻域内无限接近于点 x 0 时,相应的函数 f ( x )无限趋近于某个常数 A ,则称 A 为函数 f ( x )在点 x 0 处的 左极限 。记作
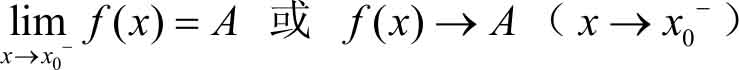
设函数 y = f ( x )在点 x 0 右侧的某个邻域(点 x 0 本身可以除外)内有定义,当自变量 x ( x > x 0 )在该邻域内无限接近于点 x 0 时,相应的函数 f ( x )无限趋近于某个常数 A ,则称 A 为函数 f ( x )在点 x 0 处的 右极限 。记作
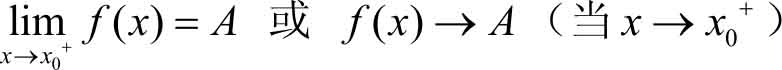
例2.4
设函数
 ,画出该函数的图像,求
,画出该函数的图像,求
 ,并讨论
,并讨论
 是否存在。
是否存在。
解 函数 f ( x )的图像如图2-7所示,由图中可以看出:
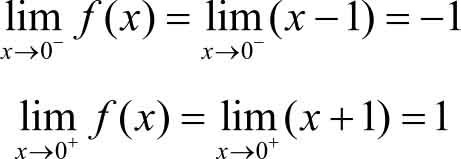
所以
 不存在。
不存在。
例2.5
设
 ,画出该函数的图像,求
,画出该函数的图像,求
 ,并讨论
,并讨论
 是否存在。
是否存在。
解 函数 f ( x )的图像如图2-8所示,结合图像分析可得:

同时可得
 。
。
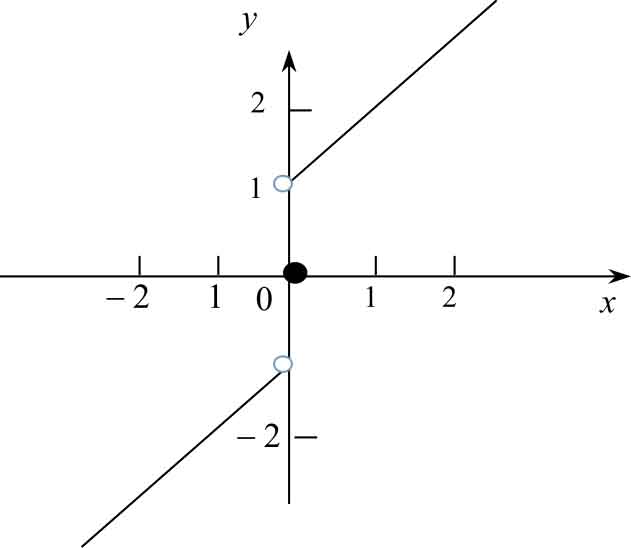
图2-7
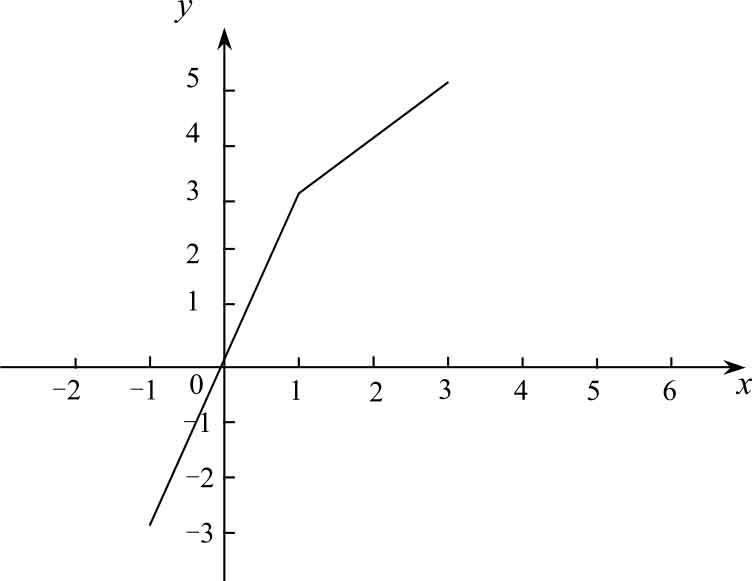
图2-8
请思考: 由左右极限定义及上述的两个例子,你对极限与左右极限存在所具有的关系有什么想法?
定理2.2
 =
A
的充要条件是
=
A
的充要条件是
 。
。
例2.6
判断
 是否存在。
是否存在。
解
当
x
>0趋近于0时,即
x
→0
+
,
 →+∞,
→+∞,
 →+∞,则
→+∞,则
 =+∞;
=+∞;
当
x
<0趋近于0时,即
x
→0
__
,
 →-∞,
→-∞,
 0,则
0,则
 =0。
=0。
由于左极限存在,右极限不存在,故
 不存在。
不存在。
由上述数列极限和函数极限的定义中可以看出,它们描述的问题都是:自变量在某一变化过程中,函数值无限趋近某个常数。因此,它们有一系列的共性,下面以 x → x 0 为例给出函数极限的性质。
性质1
(唯一性) 若极限
 存在,则极限值唯一。
存在,则极限值唯一。
即
 =
B
,则
A
=
B
。
=
B
,则
A
=
B
。
性质2
(有界性) 若极限
 存在,则函数
f
(
x
)在
x
0
的某个空心邻域内有界。
存在,则函数
f
(
x
)在
x
0
的某个空心邻域内有界。
性质3
(保号性) 若
 ,且
A
>0 (或
A
<0),则在点
x
0
的某个空心邻域(点
x
0
本身可以除外)内,有
f
(
x
)>0 (或
f
(
x
)<0)。
,且
A
>0 (或
A
<0),则在点
x
0
的某个空心邻域(点
x
0
本身可以除外)内,有
f
(
x
)>0 (或
f
(
x
)<0)。
推论
若在点
x
0
的某个空心邻域(点
x
0
本身可以除外)内,
 ,且
f
(
x
)≥0(或
f
(
x
)≤0),则
A
≥0(或
A
≤0)。
,且
f
(
x
)≥0(或
f
(
x
)≤0),则
A
≥0(或
A
≤0)。
性质 4
(夹逼准则) 如果函数
f
(
x
),
g
(
x
),
h
(
x
)在同一变化过程中(
x
→
x
0
),满足
g
(
x
)≤
f
(
x
)≤
h
(
x
),且
 ,那么
,那么
 =
A
。
=
A
。
从直观上看,该准则是显然的,当
x
→
x
0
时,函数
g
(
x
)、
h
(
x
)的值趋于常数
A
,而夹在
g
(
x
)与
h
(
x
)之间的函数
f
(
x
)的值也趋近于常数
A
,即
 =
A
。对于极限的上述 4个性质,若把
x
→
x
0
换成自变量
x
的其他变化过程,有类似的结论成立。
=
A
。对于极限的上述 4个性质,若把
x
→
x
0
换成自变量
x
的其他变化过程,有类似的结论成立。
1.观察下列数列的一般项 u n ,写出它们的极限。
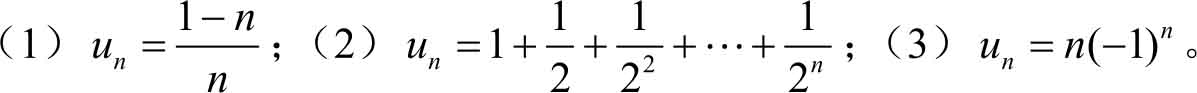
2.画出下列函数的图像并考察当 x →0时函数的极限是否存在。