





归纳类比Analogy
|
A |

归纳类比
 指的是探寻各种事例之间内在相似性的学习方法。运用类比不仅能帮助学习者理解其中蕴含的规律原理,还能提升在新情境中运用这些规律的灵活性。
指的是探寻各种事例之间内在相似性的学习方法。运用类比不仅能帮助学习者理解其中蕴含的规律原理,还能提升在新情境中运用这些规律的灵活性。
在标准化考试中(如GRE
 ),“逻辑类比”这类题目属于经典题型之一,我们不妨来尝试一下。
),“逻辑类比”这类题目属于经典题型之一,我们不妨来尝试一下。
洪水之于水滴,好比:
(a)沙滩之于海浪
(b)沙漠之于绿洲
(c)暴雪之于冰柱
(d)泥石流之于砾石
(e)倾盆大雨之于水洼
类比推理常被演绎成各种形式,广泛用于测量学习者的各项能力,尤其是词汇量、知识面、创造力等方面。除了用作测试之外,类比推理本身也是一种极为有效的学习方法,主要体现在三个方面。
·可以加深学习者对事物之间蕴含的共通原理的理解。
·在学习之后碰到类似情况时,更有可能主动运用之前学到的原理。
·能够有意识地利用类比推理来引导自己思考学习。
让我们回到上面这个“ 洪水 之于 水滴 ”的例子。首先,(a)和(e)选项看上去都很像正确答案。这是为什么呢?其原因是它们与原词组有着共同的 “表面特征” (surface features),即“水”。所谓表面特征,指的是那些一眼就能看出来的特征。不过实际上,这道题中与原词组的逻辑类比更为接近的是(d)选项,这是因为它们有着共通的 “深层结构” (deep structures),即“本身无害的事物,随着数量的积累会发生质的变化而引发大灾难”。这里所说的深层结构是指元素之间存在的内在关系。因此即便原词组说的是水。
(d)选项说的是石头,两组事物的本质关系依然是相似的。由此可见,利用类比来学习的关键在于,要从外表看似迥异的事物中找到它们的内在共通原理。图A.1中的文氏图总结了这个关键点,同时也应验了一条关于学习的普世真理: 两个例子要比一个例子的学习效果更好。
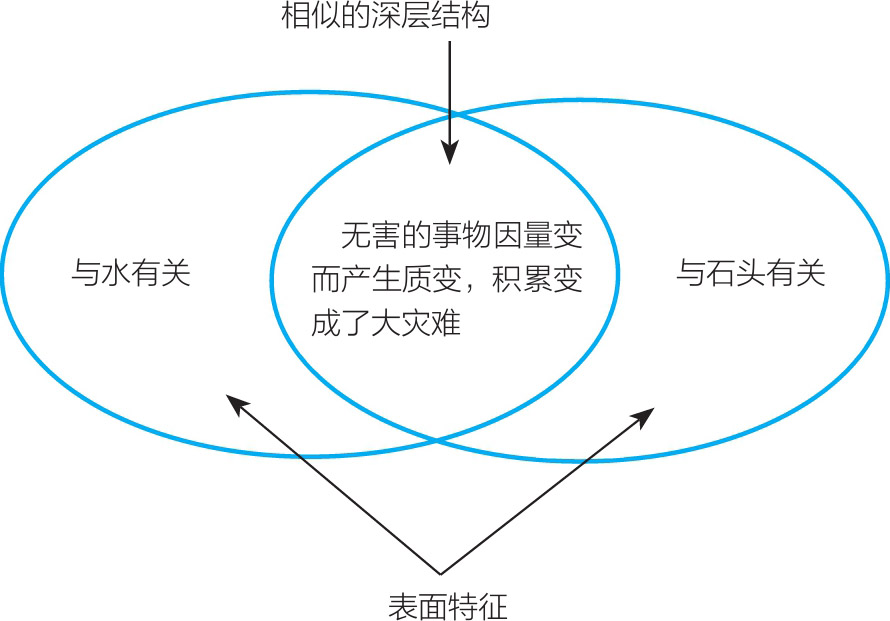
图A.1 能否成功构建出类比关系,取决于人们是否能从表象特征迥异的事物中发掘出其中相似的深层结构
在学习情境中运用类比的方法主要有两种(见图A.2)。
(1)在解释新的事物或观点时,把它类比成一个人们熟悉的例子;
(2)提供两个或更多的类比事例,让学习者探索其中共存的深层结构。
举个具体的例子,人们常常把血管类比为高速公路来辅助理解,或者把地球地层的结构类比为桃子的结构来进行阐释,等等。同样,在科研领域的最前沿,人们也常会用已知事物来类比新发现。科学史上最令人印象深刻的例子莫过于开普勒
 的万有引力定律,这一概念成功地解释了行星按椭圆形轨道运行的原理(Gentner et al.,1997)。他从太阳光芒强弱程度变化的类比中获得启发:光线照得越远,强度就会越弱,以此类推,万有引力亦是如此。虽然这个思路现在看来非常容易理解,但在当时可不是一拍脑袋灵光乍现得来的。事实上,开普勒经过多年研究才逐渐将光线与万有引力之间的类比关系勾勒出来,用来解释行星的椭圆轨道。由此可见,一个好的类比需要经过设计者仔细推敲,从而让学习者能够由已知事物出发,自然地构建起通向新事物的桥梁。
的万有引力定律,这一概念成功地解释了行星按椭圆形轨道运行的原理(Gentner et al.,1997)。他从太阳光芒强弱程度变化的类比中获得启发:光线照得越远,强度就会越弱,以此类推,万有引力亦是如此。虽然这个思路现在看来非常容易理解,但在当时可不是一拍脑袋灵光乍现得来的。事实上,开普勒经过多年研究才逐渐将光线与万有引力之间的类比关系勾勒出来,用来解释行星的椭圆轨道。由此可见,一个好的类比需要经过设计者仔细推敲,从而让学习者能够由已知事物出发,自然地构建起通向新事物的桥梁。

图A.2 两种用类比辅助学习的方法
类比的第二种应用方法是为学习者提供至少两个类比事例,然后要求他们从其中推理出共通的深层结构。研究证明这种方法的学习效果极佳。让学习者自行发现其中的规律,远比提供现成的、“喂到嘴边的”规律说明,外加一个实例要有效得多!这一点需要特别注意,因为作为学习的组织者或是知识的传授者,我们很容易忍不住提前揭晓谜底,心急火燎地把其中的奥义和盘托出,结果就是很遗憾无法为学习者留下充足的探索空间与思考时间。比方说,美国的中小学中,“先展示一个例子再讲解其原理”就是一种极为常见的教学方法(Richland,Zur,&Holyoak,2007)。但是如果我们从学习效果的角度出发,老师们可能就需要在教学方式上进行一些积极的调整。从下面这项经典的研究中我们就可以明显地看出,学习者自行总结类比规律的优势显著。在该研究中,研究人员希望了解人们思考解决邓克(Duncker)放射治疗问题的过程(Gick&Holyoak,1983)。该问题如下:
一位肿瘤病人需要进行放射治疗。如果医生要想消灭深藏在体内的肿瘤细胞,就需要使用高强度射线,但是被射线穿透的健康细胞也会被一同杀死。而如果为了保护健康细胞而减弱射线强度,却又杀不死肿瘤细胞。请问医生该怎么办呢?
为了探究如何辅助参与者依靠自己的力量得出答案,研究人员为该问题设计了几个不同的类比案例作为参考。例如,其中一个例子是:
一位将军要率领军队攻下一座城池,他必须兵分几路从不同方向进攻,因为如果让全部兵力从一个方向进攻,就会压垮护城河上的大桥。
另一个用来类比的例子则与救火有关:
消防员们想要扑灭一场大火,如果让所有水枪都从同一个方向喷射,那么水枪巨大的反作用力会使消防员难以控制;因此消防队员们用好几把水枪从不同方向喷水,保证灭火水量的同时又把反作用力控制在了合理的范围之内。
除了提供类比案例,研究人员还将其中的规律总结出来写成原理描述:
先分散力量,再集中解决目标。
看到这里,想必你一定知道问题的答案了:医生可以从几个不同的角度同时用几束强度较弱的射线集中照射肿瘤细胞。
基于上述两个例子和一段原理描述的素材,研究人员搭配出6种不同的条件组合,希望了解其中哪种组合最有利于参与者自己解答出放射治疗的问题(见图A.3)。首先,参与研究的大学生都会拿到一本资料册。每个人的资料册最后一页都会印着放射治疗问题,但并不会提示该问题与资料册中的其他内容有关。各条件组的不同之处在于资料册里面的内容,其中“例子”有三种可能性:没有类比案例、一个类比案例、两个类比案例(攻打堡垒和灭火问题),同时“原理讲解”有包含和不包含两种搭配。下表展示了一共6种不同的条件,以及各条件组中能自己解答出放射治疗问题的学生数比例。
通过两个类比例子进行推理而得出答案的学生人数(62%,52%),要比没有参考任何类比的学生数(28%,18%)高出一倍多;同时,参考了两个类比例子却没有读到规律讲解的学生数(52%),也比读过规律外加一个类比例子的学生表现得好(32%)。这有点让人摸不着头脑,毕竟讲解原理再搭配一个例子是大家普遍采用的学习和教学方法,然而实际效果却并不那么理想。这是为什么呢?
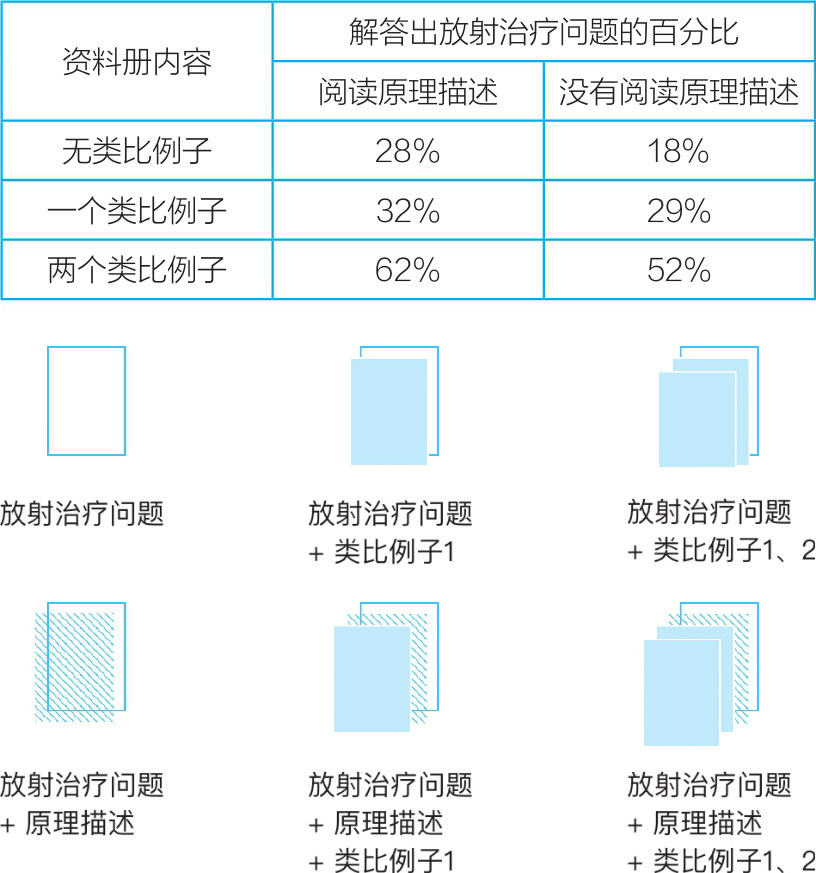
图A.3 不同实验条件组中,例子与规律描述的组合方式及相应条件组中自己解答出放射治疗问题的学生比例
问题出在学会了某个概念并不代表真正懂得该何时应用它。之所以原理加单一例子的组合效果不尽如人意,是因为学习者并没有领悟到该原理适用场景的多样性。例如,那些读到兵分几路攻打堡垒案例的学生,虽然学习了相应的规律原理,但是却无法举一反三地将这一原理应用于其他情境,反而是看过两个不同情境例子的学生更能切身体会这一点。因此,我们要尽可能展示出某一原理应用场景在表面特征上的多样性,来帮助学习者打开思路,提升应用的灵活性。
类比推理可以帮助学习者透过现象看本质。这就好比从麸皮中筛出麦粒(请允许我们在此用了个略显夸张的类比)。然而,很多时候人们还是会过度依赖表面特征来做判断,却忽略了事物中蕴含的深层结构。下面这项研究充分体现了这一点(Ross,1984),参与实验的大学生学习计算概率的公式,如排列和组合的计算公式等
 。作为研究的一部分,学生们会结合一种物品来学习组合数的计算(例如借助小汽车模型),学习排列数的计算时则会借助另一种物品(例如骰子)。在实验后测中,如果测试题目讨论的物品与学习案例中的一致(即学的时候计算小汽车的组合排列,后测题目也围绕小汽车来讨论),学生们的表现就都还基本令人满意。至此,一切顺利。
。作为研究的一部分,学生们会结合一种物品来学习组合数的计算(例如借助小汽车模型),学习排列数的计算时则会借助另一种物品(例如骰子)。在实验后测中,如果测试题目讨论的物品与学习案例中的一致(即学的时候计算小汽车的组合排列,后测题目也围绕小汽车来讨论),学生们的表现就都还基本令人满意。至此,一切顺利。
然而当测试题目中的物品互换时,问题出现了(见图A.4)。例如当组合数题目用的不再是小汽车而是骰子时,测试结果就会很糟糕,甚至还不如用一个在讲解时没出现过的全新物品(既不用小汽车也不用骰子,比如用小星星)。或许我们可以这样理解这一现象:由于学生并没有透彻理解排列和组合计算中的深层原理,于是在选择要用哪个计算公式时,判断依据是题目所涉及的物品这一表面现象,而非问题的本质。比如说,学生们会错误地认为,“与骰子相关的计算都是要算排列数,这道题和骰子有关,所以是排列问题。”我们把这类错误称为
负迁移
 :
人们把学到的东西用在了错误的地方。这种情况之所以出现,主要是因为人们尚未辨识出问题的深层结构,所以只能借助显而易见的表面特征作为线索来处理问题。
:
人们把学到的东西用在了错误的地方。这种情况之所以出现,主要是因为人们尚未辨识出问题的深层结构,所以只能借助显而易见的表面特征作为线索来处理问题。
类比则可以帮助学习者进行
正迁移
 。在放射治疗的问题中,参考过两个类比例子的学生就成功实现了正迁移,他们能够在新情境中合理地运用所学知识。如果我们希望帮助上述研究中那些没学好排列组合的学生的话,就应该在讲解排列和组合的时候,同时用上小汽车和骰子的例子,并让他们思考题目之间的共通之处,随后再讲解公式与原理。
。在放射治疗的问题中,参考过两个类比例子的学生就成功实现了正迁移,他们能够在新情境中合理地运用所学知识。如果我们希望帮助上述研究中那些没学好排列组合的学生的话,就应该在讲解排列和组合的时候,同时用上小汽车和骰子的例子,并让他们思考题目之间的共通之处,随后再讲解公式与原理。
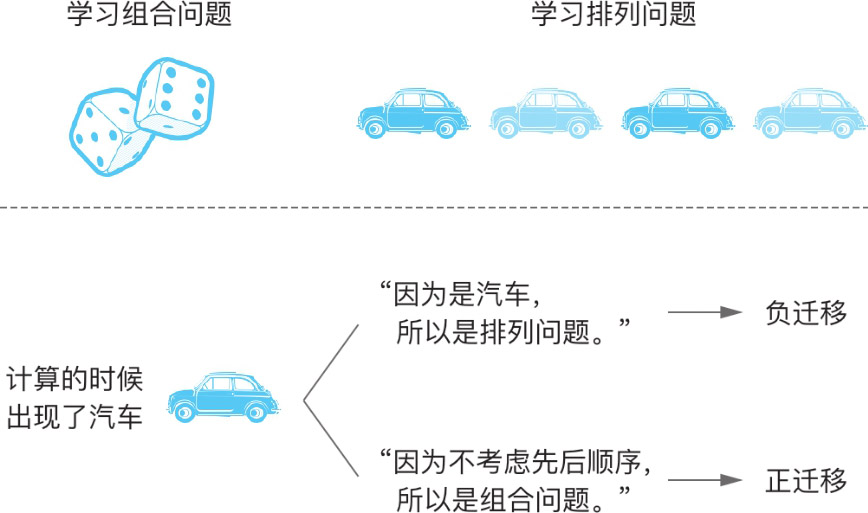
图A.4 组合数和排列数计算中的正迁移和负迁移
读到这里你可能不禁会问,“那么我们该如何判断通过类比的学习是有效的呢?”这是个好问题。比方说,一种思路是给学习者布置一个深层结构相同,但表面特征不同的“迁移任务”。这个任务最好是设定在全新的情境下,而且不要提示它与之前所学的哪部分内容相关。如果学习者能自主使用之前从类比例子中学到的知识点,那就说明他们确实掌握了问题的深层结构。例如,在一项研究中,一群高二学生需要探究密度与速度之间的类比关系(Schwartz,Chase,Oppezzo,&Chin,2011)(可能你也会想,密度和速度之间能有什么类比关系呢?其实二者的共通点是它们都运用到了比例:密度=质量/体积,速度=距离/时间)。随后,学生们要解答一个与弹簧弹性系数有关的问题(也是一个用比例计算的物理量,弹性系数=质量/距离)。结果这些学生还真的倾向于主动借助比例的概念来解题。
通过类比学习所获得的关键成果在于,学习者将核心概念应用于新情境的能力。这个结果意味深远,因为我们希望学习者在独立解决问题的时候,能够依靠自己的力量判断问题的本质,从而选择正确的应对方式。
人们可以自己学会用类比的方式去思考并辅助学习过程。一项在3~4岁儿童中开展的研究(Brown&Kane,1988)极好地证明了这一点。这项研究通过一组一组的小话剧来教学。在第一组话剧的上半场,一位农场伯伯想取一瓶放在高处的杀虫剂却够不到货架的最上层。小朋友们会被问到农场伯伯该怎么办。之后,小朋友们要首先尝试自己解决问题,然后再观看研究人员展示一种办法:用稻草垛一层层地叠起来,然后再爬上去拿东西。在第一组话剧的下半场,修理车间的一位师傅想要拿货架上面的润滑油,也是够不着。孩子们同样先尝试自己解决,如果想不出办法,研究人员就会将答案展示给他们:机械师把轮胎堆起来再爬上去。之后孩子们还要观看几组围绕其他类似问题的话剧。例如有一组话剧都是围绕用长杆去够东西这个问题。
在第一组话剧中,孩子们还不会把从上半场学到的方法(堆叠草垛)运用到下半场的问题中(堆叠轮胎)。然而到了第三组话剧中,这些学龄前儿童就已经学会去思考上半场与下半场之间的类比关系。他们不再把两场话剧中的问题看作不相关的两个情境,而是学会了从两个问题中寻找共通的类比关系。理想情况下,帮助孩子们学会寻找类比关系,可以提高他们在不同事例中深度思考的学习能力。
运用类比的学习过程中容易出现两类问题,需要我们格外注意。首先,学习者可能无法从类比中总结出蕴含其中的深层结构,或是干脆读出了目标内容之外的东西。比如,学生们类比了原子结构与太阳系结构之后,可能会得出“这里面所有的东西都是球”这一规律,却忽视了按轨道运行、质量集中在核心、组成元素散布在相对较大的空间中等关键特征。当然了,客观来说这类问题可能只是美中不足,因为即便学习者没能一下子看出来我们想让他们看出来的类比关系,努力思考深层结构和共通原理的过程,也足以作为构建更通透理解的良好铺垫(请参考本书章节J)。
而更为严重的问题是,为目标特征选择的类比不恰当,类比关系无法准确反映问题。例如,随着科学技术的飞速发展,当今人们对原子的了解越来越精准,原子结构与行星轨道的概念类比已经不再适用(见图A.5)。若是要举一个生活中更常见的例子,那么最耳熟能详的莫过于电流与水流的类比。人们常用水管中的水流来类比电线中的电流。这确实能帮助人们直观地理解电流的概念,但同时也引入了一个错误概念:如果根据这个类比来推理,那么点亮一串彩灯时小灯泡应当是按顺序逐个亮起,因为电流(水流)要流经导线(水管)。这里出现的问题并非类比推理的逻辑有误,而是类比本身就不严谨!更准确的类比描述应当是,水管中已经充满水,打开水龙头后管子里的水会同时流动起来。总而言之,在利用类比的时候,务必要选择合适准确的例子,谨防误人子弟。当然,刚开始学习的时候,可以先用一个简单的例子进行类比,随着学习者的理解不断加深,再用更准确的类比例子取而代之。但这里还要再提醒一句,如果一开始学习时的理解有误,早期形成的误解在之后可能很难消除(请参考本书章节U)。
说过了两种常见的问题,我们再结合实践中的情况进行讨论。乍看上去,要求学习者自己为学习内容选择类比例子应该是个不错的主意。但这又会带来另一个问题,因为人们总会不由自主地在已知的范围内寻找类比对象,而很难从全新的角度来思考问题的本质。比如,如果我们邀请你找一个用来类比DNA
 的例子,你可能会想到工程蓝图(二者都是复杂系统的核心指南)、一串编程指令(二者都是用简单而有限的代码进行组合,创造出无限可能),或是一条麻绳(二者都是螺旋缠绕的形态)。虽然这些例子都很棒,但都只从一个我们已经熟悉的角度来体现DNA的某一特征,因此这些类比并没有带来多少额外的价值。因此,如果我们想要发挥出类比案例所能带来的更大学习价值,则应邀请更多人一起加入构思类比的过程,然后再一起分享讨论,看看哪个类比对于表达目标内容更为贴切。这既能帮助学习者了解挑选优质类比的标准,又能促进对目标概念本身的深入理解。
的例子,你可能会想到工程蓝图(二者都是复杂系统的核心指南)、一串编程指令(二者都是用简单而有限的代码进行组合,创造出无限可能),或是一条麻绳(二者都是螺旋缠绕的形态)。虽然这些例子都很棒,但都只从一个我们已经熟悉的角度来体现DNA的某一特征,因此这些类比并没有带来多少额外的价值。因此,如果我们想要发挥出类比案例所能带来的更大学习价值,则应邀请更多人一起加入构思类比的过程,然后再一起分享讨论,看看哪个类比对于表达目标内容更为贴切。这既能帮助学习者了解挑选优质类比的标准,又能促进对目标概念本身的深入理解。
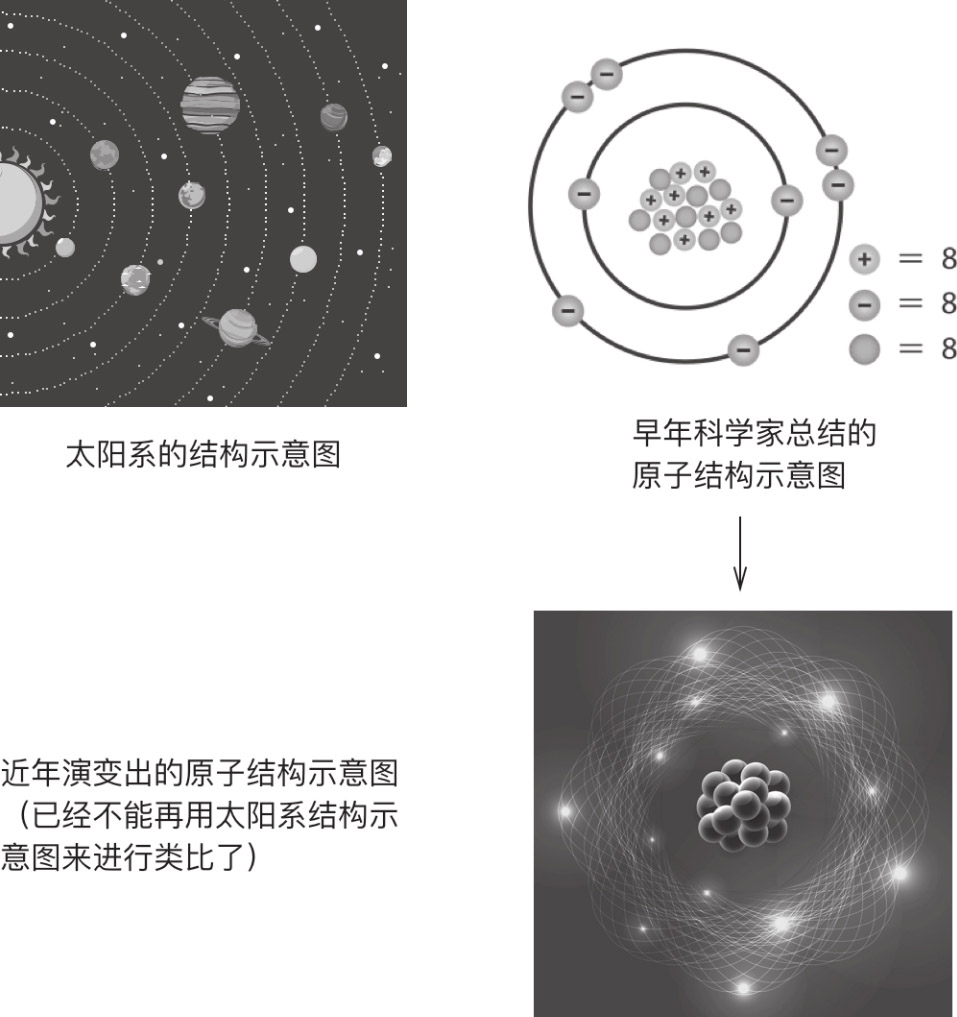
图A.5 太阳系和原子结构模型的类比已经过时了,人们对原子结构的最新理解已与太阳系的结构不同
假如我们邀请你来讲解与大脑神经通路有关的内容,需要用到下面这个类比:

·基础类比组合描述了人们非常熟悉的事物之间的关系。
·目标类比组合与基础类比组合有诸多相似之处:
·两组关系都可以总结为“……是……用来通行的长长的路径”。
·两组关系中,路径上运行的实体,都经由岔路进入或离开主干路。
·两组关系中,路径出入口的位置都是确定的,不是随便从哪儿都能进入或离开路径。
有时人们对基础类比组合 太过 了解,以至于会一不小心误把一些不应进行类比的细节错误地代入目标类比组合的关系中去。例如,在这个例子中,高速路是可以由 其他 道路进出的 一条 道路。但白质纤维束则是由一捆相互平行的、被称为神经轴突的通路构成的。神经信号从起点到达终点只会经过一条轴突。如果按照高速路的类比来学习有关大脑的知识,人们可能会误认为神经信号可以从一条轴突跳跃到另一条轴突(就像高速路上变换车道一样),想走哪条道就走哪条道。
如果理解中遗留下了不准确的地方,人们就可能会按照自己对类比例子的理解去误解目标内容。整体上讲,准确的类比是我们的理想选择,当然也不用因噎废食,学习的时候如果遇到了不那么准确的类比例子,只要搞明白其中不准确、有误导性的地方就行。
核心的学习原理是什么
从两个或两个以上、外表看似迥异的例子之间找到共通的规律。
·为了解释全新的事物或观点,用学习者熟悉的东西做类比。
·为了让学习者探索并总结出事物中蕴含的深层结构,给出至少两个类比事例。
对学习什么有帮助,举个例子
请问 树干上长得像枯树枝的竹节虫与非洲金黄草丛中的金毛狮王 之间有什么相似点(见图A.6)?让学习者寻找其中的类比关系,可以帮助他们理解知识重点(如伪装),而如果只给出其中一个例子,学习者很可能会将注意力放到其中一些无关紧要的细节上,比如狮子的样子多么伟岸,长得像不像《狮子王》里的辛巴,等等。类比可以促进学习者对于事物中蕴含原理的理解,并更有可能让学习者在新的问题情境中合理运用原理。这也是教育的最高目标之一,让学生把校内习得的知识技能,应用于校外真实场景中的实际问题,做到学以致用。

图A.6 图中能看出什么共通的深层结构?你能看出右上图中隐藏在碎石里的小螃蟹吗?
为什么会有用
类比可以帮助学习者通过自己熟悉的、已知的内容来理解新概念。类比是一种极为强大的学习方法,因为它可以帮助人们学到“换汤不换药”中的“药”。(请问聪明的读者,这个类比使用得恰当吗?)
能解决什么样的学习问题
·学习者理解一个新概念有些困难。
·学生无法想象地球与太阳之间的相对大小。
·学习者似乎只关注表面细节,却忽略了核心概念或原理。
·在一节讲解动物保护色的课上,一位小朋友开心地比较着各种动物不同的表皮颜色,而不去关心动物的颜色都能与周围环境融为一体这个关键点。
·学习者无法将学到的知识应用到新的情境中。
·学生在课堂测验中做得很好,但在期末考试中却考砸了。
·学生知道用线性斜率来计算速度(d/t),但却不会将斜率用在计算密度(m/v)的新问题中。
使用的范例
·用一个熟悉的例子来解释一个相对抽象的新概念。
·电流就像充满于水管中的水。
·让学习者比较不同事物之间的相似性。
·蝴蝶、海蜇、花粉在远距离移动时的相似点是什么?
·从罐子中拿弹珠和掷骰子有什么相似的地方?
容易出现的问题
·类比可能会引入误解或错误概念:例如把神经元上的神经信号比作道路上的汽车,但要指出神经信号(汽车)可没法停在神经元上(路上)。
·学习者有可能抓不住类比中的关键点,尤其是在类比关系不直观,或是对于类比对象本身也理解得不扎实的时候。