第2章
动力学、混沌和预测

再一次一无所知 ，从头开始……这让我很开心。

对于我们来说平常大小的事物，人们为之写诗的那些——云彩、水仙花、瀑布，它们对于我们，就好像天堂对于古希腊人，充满了神奇……现在也许是最好的时代，你曾以为正确的东西几乎都是错的。

——斯托帕德（Tom Stoppard），
《阿卡狄亚》（ Arcadia ）

动力系统理论（动力学，dynamics）关注的是对系统的描述和预测，其所关注的系统通过许多相互作用的组分的集体行为涌现出宏观层面的复杂变化。动力一词意味着变化。而动力系统则是以某种方式随时间变化的系统。下面是动力系统的一些例子：

◆太阳系（行星位置随时间变化）；

◆心脏（周期性跳动）；

◆大脑（神经元不断激发，神经递质在神经元之间传递，突触强度变化，整个系统不断变化）；

◆股票市场；

◆世界人口；

◆全球气候。

不仅这些，其他你想得到的系统几乎都是动力系统。甚至岩石在地理时间尺度上也是变化的。动力系统理论以最一般化的方式描述系统的变化，描述变化可能的宏观形态，以及对于其变化能够做出怎样的估计和预测。

近年来，动力系统理论很受大众关注，这是因为它的一个分支——混沌学——发现了一些让人着迷的结果。但实际上它的历史很悠久，同许多学科一样，它可以追溯到古希腊哲学家亚里士多德。

动力系统理论的起源

亚里士多德（图2.1）是目前所知的最早论述运动理论的人之一，他的理论流行了1500多年。他的理论有两个主要原理，后来发现都是错的。首先，他认为地面上的运动与天上的不同。他认为地面上的物体在受到力推动时才会沿直线运动；没有力，物体就会保持静止。而在天上，行星等天体是围绕着地球不断做圆周运动。另外，亚里士多德认为，在地面上，不同物质组成的物体运动方式也不一样。比如，他认为石头落向地面是因为石头主要是由土元素组成，而烟会上升则是因为烟是由气元素组成。在天上也是一样，越重的物体中的土元素越多，下落也越快。

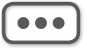
同以前许多理论家一样，亚里士多德在构造理论时没有考虑实验验证。他的方法是用逻辑和常识引导理论；用实验对理论进行验证的重要性在当时还没有被认识到；亚里士多德的思想影响很大，一直统治着西方科学，直到16世纪——伽利略（图2.2）登上历史舞台。

伽利略、他之前的哥白尼以及与他同时代的开普勒是实验和观察科学的先驱。哥白尼提出行星不是围绕地球而是围绕太阳运行。（伽利略在宣扬这种观点时受到了天主教会的强烈阻挠，最后被迫公开宣布放弃。直到1992年教会才正式承认对伽利略的迫害是错误的。）在16世纪初，开普勒发现行星的运行轨迹不是圆而是椭圆，他还发现了关于这种椭圆运动的几条定律。

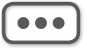
哥白尼和开普勒只研究了天体的运动，而伽利略不仅研究天上的运动，也研究地面上的，他做了一些我们现在在中学物理课上会学到的实验：单摆、沿斜面滚动的小球、自由落体、镜面光线反射。不过伽利略可没有我们现在使用的那些精密实验设备，据说他通过数脉搏来计算单摆的摆动周期，还在比萨斜塔上下落物体以测量重力的效应。这些经典实验彻底改变了对运动的理解，并且直接驳斥了长期盛行的亚里士多德的观点。与直觉不同，静止并不是物体的自然状态；相反，要施加力才能让运动物体停下来。不管物体多重，在真空中下落的速度都是一样的。最具革命性的是，地面上的运动定律居然也能解释天上的运动。自从伽利略之后，有了实验观察作为基础，科学革命的发生就不可避免了。

动力学历史上最重要的人物是牛顿（图2.3），牛顿生于伽利略死后那一年。他可以说是凭一己之力创建了动力学。为了创建动力学，他还要先发明微积分——描述运动和变化的数学。

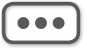
物理学家将对运动的总体研究称为机械力学（mechanics）。这个词源自古希腊，因为古典观点认为，所有运动都可以用杠杆、滑轮、轮轴等简单“机械”的动作组合来解释。牛顿的工作现在被称为经典力学。力学分为两部分：描述物体如何运动的运动学（kinematic），以及解释物体为何遵循运动学定律的动力学。例如开普勒定律就是运动学定律，它们描述了行星如何运动（以太阳为焦点沿椭圆运动），但没有解释行星为何这样运动。牛顿的定律则是动力学的基础，它们用力和质量作为基本概念解释了一切物体的运动，包括行星。

下面是著名的牛顿三大定律：

1.在任何情况下，一切物体在不受外力作用时，总保持静止或匀速直线运动状态。

2.物体的加速度与物体的质量成反比。

3.两个物体之间的作用力和反作用力，在同一条直线上，大小相等，方向相反。

牛顿的伟大之处在于他认识到这些定律不仅适用于地面上的物体，对天上的物体也同样适用。匀速运动定律是伽利略首先提出来的，但是他认为只适用于地面上的物体。而牛顿则认为这条定律对行星应该也适用，并且认识到需要用力（引力）来解释椭圆运动方向的不断变化。牛顿的另一重要贡献是提出了万有引力定律：两个物体之间的引力与两者质量的乘积成正比，与两者距离的平方成反比。牛顿深刻认识到这条定律适用于宇宙中一切事物，无论是行星还是苹果，这个认识是现代科学的基石。正如他说的：“自然简单而自足， 对宏大物体的运动成立的，对微小物体也同样成立。”

牛顿力学描绘了一幅“钟表宇宙”的图景：设定好初始状态，然后就遵循着三条定律一直运行下去。数学家拉普拉斯认识到其中蕴含了可以如钟表般精准预测的观念：他在1814年断言，根据牛顿定律，只要知道宇宙中所有粒子的当前位置和速度，原则上就有可能预测任何时刻的情况。 在20世纪40年代计算机被发明出来之后，这种“原则上”的可能似乎有可能变成现实了。

对预测的重新认识

然而，20世纪的两个重要发现表明，拉普拉斯的精确预测的梦想，即使在原则上也是不可能的。1927年，海森堡（Werner Heisenberg）提出了量子力学中的“测不准原理”，证明不可能在准确测量粒子位置的同时，又准确测量其动量（质量乘以速度）。对于其位置知道得越多，对于其动量就知道得越少，反过来也是一样。不过，海森堡原理还只是限制了对量子世界微观粒子的测量，大多数人都只是觉得它挺有趣，但是对宏观尺度上的预测——比如天气预报——应该没有多大影响。

然而混沌的发现给了精确预测的梦想最后一击。混沌指的是一些系统——混沌系统——对于其初始位置和动量的测量如果有极其微小的不精确，也会导致对其的长期预测产生巨大的误差。也就是常说的“对初始条件的敏感依赖性”。

对于一些自然系统，并没有这个问题。如果你对初始条件的测量不是十分精确，你的预测即使不全对，也会八九不离十。例如天文学家在测量行星位置时即使误差较大，也还是能准确预测日食。而对初始条件的敏感依赖性指的是，如果系统是混沌的，在测量初始位置时即使只有极其微小的误差，在预测其未来的运动时也会产生巨大的误差。对于这样的系统（飓风就是例子），一点点误差，不管多小，也会导致长期预测很不精确。

这一点很不符合直觉，事实上，很长一段时间里，科学家们都认为这不可能。然而，混沌现象在很多系统中都被观测到了，心脏紊乱、湍流、电路、水滴，还有许多其他看似无关的现象。现在混沌系统的存在已成为科学中公认的事实。

现在已无法说清楚是谁最先意识到可能存在这类系统。远在量子力学出现之前，就有很多人提出了对初始条件敏感依赖性的可能性。例如，物理学家麦克斯韦（James Clerk Maxwell）在1873年就猜想，有些量的“物理尺度太小， 以致无法被有局限性的人类注意，却有可能导致极为重要的结果”。

第一个明确的混沌系统的例子可能是19世纪末由法国数学家庞加莱（Henri Poincaré）（图2.4）给出。庞加莱是现代动力系统理论的奠基者，可能也是贡献最大的人，大力推动了牛顿力学的发展。庞加莱在试图解决一个比预测飓风简单得多的问题时发现了对初始条件的敏感依赖性。他试图解决的是所谓的三体问题（three-body problem）：用牛顿定律预测通过引力相互作用的三个物体的长期运动。牛顿已经解决了二体问题。但没想到三体问题要复杂得多。在向瑞典国王表示敬意的一次数学竞赛中，庞加莱将其解决了。竞赛主办方提供2500瑞典克朗奖励解决“多体”问题：用牛顿定律预测任意多个相互吸引的物体的未来运动。提出这个问题是为了确定太阳系是否稳定，行星是会维持还是会偏离目前的轨道？庞加莱想先试着解决三体问题。

他并没有完全成功——这个问题实在太复杂了。但是他的尝试很精彩，所以最后还是赢得了奖金。牛顿发明了微积分，而庞加莱为了解决这个问题也创建了一个新的数学分支——代数拓扑（algebraic topology）。拓扑学是几何学的扩展，正是在研究三体问题的几何结果的过程中，庞加莱发现了对初始条件的敏感依赖性。下面是他对此的总结：

如果我们能知道自然界的定律1和宇宙在初始时刻的精确位置，我们就能精确预测宇宙在此后的情况。但是即便我们弄清了自然界的定律，我们也还是只能近似地知道初始状态。如果我们能同样近似地预测以后的状态，这也够了，我们也就能说现象是可以预测的，而且受到定律的约束。但并不总是这样，初始条件的细微差别有可能会导致最终现象的极大不同。前者的微小误差会导致后者的巨大误差。预测变得不可能……

换句话说，即便我们完全知道了运动定律，两组不同的初始条件（在这里是指物体的初始位置、质量和速度），即使差别很小，有时候也会导致系统随后的运动极为不同。庞加莱在三体问题中发现了一个这样的例子。

直到电子计算机出现之后，科学界才开始认识这类现象的意义。庞加莱远远超越了他所处的时代，他意识到对初始条件的敏感依赖性将会阻碍对天气的长期预报。他的远见于1963年被证实，气象学家洛伦兹（Edward Lorenz）发现， 即使是很简单的计算机气象模型，也会有对初始条件的敏感依赖性。现在虽然有了高度复杂的气象计算模型，天气预报也最多只能做到大致准确预测一个星期。目前还不清楚这个局限是否是天气的混沌本质导致的，也不知道通过收集更多数据和构造更好的模型，可以将这个局限推进多远。

线性兔子和非线性兔子

现在我们再详细了解一下对初始条件的敏感依赖性。混沌系统中初始的不确定性到底是如何被急剧放大的呢？关键因素是非线性。对于线性系统，你可以先了解其组成，然后将它们合到一起。当我的两个儿子和我一起做厨艺时，他们喜欢轮流加原料。杰克放两杯面粉，跟着尼克又加一杯糖。结果呢？三杯面粉和糖的混合物，整体等于部分之和。

对于非线性系统，整体则不等于部分之和。杰克放了两杯苏打粉，尼克又加了一杯醋。整个事情就不可收拾了（你可以自己在家里试试）。有什么后果？你会得到大量醋、苏打粉和二氧化碳混合的泡泡。两者之间的区别在于：前面的糖和面粉不会产生反应生成新的东西，而后者的醋和苏打粉会剧烈反应，产生很多二氧化碳。

还原论者喜欢线性，而非线性则是还原论者的梦魇。理解线性和非线性的区别很有用，值得研究一下。为了更好地理解非线性以及混沌现象，我们要研究一点点简单的数学，借用一个经典的生物群体数量动力学模型来阐释线性和非线性。设想你养了一群兔子，兔子会配对生小兔子，每对兔子父母每年会生4只小兔子然后死去。图2.5显示了兔子的繁殖状况。

很显然，如果不受限制，兔子的数量会每年翻番（这意味着兔子很快会接管这个星球，乃至太阳系和整个宇宙，不过我们暂时还不用担心）。

这是一个线性系统： [19] 整体等于部分之和。我想让它们做什么呢？我们先将4只兔子分开放到两个岛上，每个岛上2只。然后让兔子继续繁殖。图2.6显示了繁殖两年的情形。

两边都是每年翻番。不管是哪一年，如果你把两个岛的兔子加起来，你得到的数量还是与没分开时一样多。

如果以当年的兔子数量为横坐标，以次年的兔子数量为纵坐标，将各年的数据标上去，你将会得到一条直线（图2.7）。这就是为什么称之为线性系统。

但是如果考虑到种群数量增长所受的限制，情况会怎样呢？这会使得增长规则变为非线性的。假定前面的规则仍然成立，每对兔子每年生4只小兔子然后死去。不过现在有些小兔子会因为太过拥挤没有繁殖就死去。研究种群数量的生物学家常用逻辑斯蒂模型 （Logistic model）描述这种情形下群体数量的增长。这个模型以一种简化方式描述群体数量的增长。你设定好出生率、死亡率（由于种群数量过多导致的死亡概率）以及最大种群承载能力（栖息地所能承载的种群数量上限），然后将这一代的种群数量代入逻辑斯蒂模型，就能算出下一代的种群数量。在这里我不给出逻辑斯蒂模型的具体形式 [21] （注释中有），你可以在图2.8中看到它的变化情况。

举个简单的例子，设出生率为2，死亡率为0.4，承载力为32，第一代有20只兔子。用逻辑斯蒂模型算出第二代为12只。将新的种群数量再代进去，又可以得出第三代仍然是12只兔子存活。此后的兔子数量将一直维持在12只。

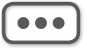
如果将死亡率降到0.1（其他参数不变），会有些有趣的事情发生。根据模型可以得出第二代为14.25只兔子，第三代则为15.01816只。

等一下！怎么会有0.25只兔子，还有稀奇古怪的0.01816只？在真实世界中显然是不可能的，不过这只是模型，允许兔子数量为小数。这样在数学上简单些，而且预测的兔子数量仍然大致符合实际。所以这里我们无须为此担心。

将算出的种群数量再代进去计算下一代的种群数量，这个不断重复的过程即所谓的“对模型进行迭代”。

如果将死亡率恢复成0.4，承载力翻一倍变成64，结果又会怎样呢？根据模型我们发现，从20只兔子出发，9年后种群数量会变为接近24的一个值，然后停在那里。

你可能注意到了这些例子中的种群变化比前面单纯每年翻番的情形复杂得多。这是因为引入了种群数量过多导致的死亡，模型变成了非线性的。其图形不再是直线，而是抛物线（图2.8）。逻辑斯蒂模型中的群体数量变化不再简单等于部分之和。为了说明这一点，我们将20只兔子分为两群，每群10只，再对各群进行迭代（参数同前面一样，出生率为2，死亡率为0.4）。图2.9为迭代结果。

第一年，前面是20只兔子只剩下12只，而分成两群后，每群有11只，总共22只。整体的变化不再等于各部分的变化之和。

逻辑斯蒂映射

许多研究这一类事物的科学家和数学家使用逻辑斯蒂模型的一个简化形式，逻辑斯蒂映射（logistic map），它也许是动力系统理论和混沌研究中最著名的方程。逻辑斯蒂映射中出生率和死亡率的效应被合成一个数，记作R。种群规模用“承载率”替代，记为x。这个简化模型问世之后，科学界和数学界很快就将种群规模、承载力等与现实世界的联系抛到脑后，转而着迷于这个方程本身，因为它的特性太让人震惊了。现在我们也来体验一下。

下面就是这个方程，其中x t 是当前值，x t+1 则是下一步的值：

我给出逻辑斯蒂映射的方程是为了向你展示它有多简单。事实上，它是能抓住混沌本质——对初始条件的敏感依赖性——的最简单的系统之一。1971年，数学生物学家梅（Robert May）在著名的《自然》杂志上发表了一篇文章 分析逻辑斯蒂映射，引起了种群生物学家的关注。在此之前也有一些数学家对其进行了详细分析，包括乌拉姆（Stanislaw Ulam）、冯·诺依曼（John von Neumann）、梅特罗波利斯（Nicholas Metropolis）、保罗·斯坦（Paul Stein）和米隆·斯坦（Myron Stein）。 但它真正变得有名是在20世纪80年代，物理学家费根鲍姆（Mitchell Feigenbaum）利用它展示了一大类混沌系统的共性。由于其显然的简单性和深厚的历史，它成了介绍动力系统理论和混沌的一些主要概念的完美载体。

如果我们让R的值变化，逻辑斯蒂映射就变得非常有趣。我们先从R=2开始。x的初始值x 0 也必须介于0和1之间，姑且设为0.5。将它们代入逻辑斯蒂映射，得出x 1 为0.5。同样，x 2 也是0.5，后面也一样。因此，如果R=2，种群初始值为最大值的一半，以后就会一直不变。

现在让x 0 =0.2。你可以自己用计算器算一下（我用的一个最多显示7位小数的计算器）。结果更有意思了：

x 0 =0. 2

x 1 =0. 32

x 2 =0. 4352

x 3 =0. 4916019

x 4 =0. 4998589

x 5 =0. 5

x 6 =0. 5

……

最终结果是一样的（永远是x t =0.5），但是迭代了5次才得到。

用图可以看得更清楚。图2.10是x t 在前20步的值的图形。我用线将这些点连起来了，这样可以更清楚地看到，随着时间推移，x迅速收敛到0.5。

如果x 0 很大，比如0.99，又会怎样呢？图2.11显示了得到的图形。

最终的结果还是一样的，不过过程要长一些，波动也更剧烈。

你可能已经猜到了：只要R=2，x t 最终都会到达0.5，并停在那里。0.5正是所谓的不动点（fixed point）：到达这一点所花的时间依赖于出发点，但是一旦你到达了那里，你就会保持不动。如果你愿意，可以让R=2.5，再试一下，同样你会发现系统总是到达一个不动点，不过这次不动点是0.6。

R=3. 1的情形更有趣。逻辑斯蒂映射的变化更加复杂了。图2.12是x 0 =0.2时的图形。

在这个例子中，x永远也不会停在一个不动点；它最终会在两个值（0.5580141和0.7645665）之间振荡。如果将前者代入方程，就会得到后者，反过来也是一样，因此振荡会一直持续下去。不管x 0 取什么值，最后都会形成这个振荡。这种最终的变化位置（无论是不动点还是振荡）被称为“吸引子”，这个说法很形象，因为任何初始位置最终都会“被吸引到其中”。

往上一直到R等于大约3.4，逻辑斯蒂映射都会有类似的变化：在迭代一些步骤后，系统会在两个不同的值之间周期振荡（最终的振荡点由R决定）。因为是在两个值之间振荡，系统的周期为2。

但是如果R介于3.4和3.5之间，情况又突然变了。不管x 0 取何值，系统最终都会形成在四个值之间的周期振荡，而不是两个。例如，如果R=3.49，x 0 =0.2，最终的结果就像图2.13那样。

x的值很快就开始在四个不同的值之间周期振荡（如果你想知道，它们分别大约是0.872，0.389，0.829和0.494）。也就是说，在3.4和3.5之间的某个R值，最终的振荡周期突然从2增到4。

在3.54和3.55之间的某个R值，周期再次突然倍增，一下跃升到8。在3.564和3.565之间的某个值周期跃升到16。在3.5687和3.5688之间周期又跃升到32。周期一次又一次倍增，前后R的间隔也越来越小，很快，在R大约等于3.569946时，周期已趋向于无穷。在此之前，逻辑斯蒂映射的变化大致都可以预测。如果R值给定，从任何x 0 点出发的最终长期变化都能预测得到：R小于3.1时会到达不动点，R介于3.1和3.4之间时会形成双周期振荡，等等。

但是当R等于大约3.569946时，x的值不再进入振荡，它们会变成混沌。 下面解释一下。将x 0 ，x 1 ，x 2 ……的值组成的序列称为x的轨道。在产生混沌的R值，让两条轨道从非常接近的x 0 值出发，结果不会收敛到同一个不动点或周期振荡，相反它们会逐渐发散开。在R=3.569946时，发散还很慢，但如果将R设为4.0，我们就会发现轨道极为敏感地依赖于x 0 。我们先将x 0 设为0.2，对逻辑斯蒂映射进行迭代，得到一条轨道。然后细微地变动一下x 0 ，让x 0 =0.2000000001，再对逻辑斯蒂映射进行迭代，得到第二条轨道。图2.14中的实心圆圈连成的实线就是第一条轨道，空心圆圈连成的虚线则是第二条轨道。

这两条轨道开始的时候很接近（非常接近，以至于实线轨道把虚线轨道都盖住了），但在大约30次迭代之后，它们明显分开了，很快就不再具有相关性。这就是“对初始条件的敏感依赖性”的由来。

我们已经看到有三种不同的最终状态（吸引子）：不动点、周期和混沌（混沌吸引子有时候也称为“奇怪吸引子”）。吸引子的类型是动力系统理论刻画系统行为的一种方式。

我们再仔细来看看混沌行为到底有多不寻常。逻辑斯蒂映射极为简单，并且完全是确定性的：每个x t 值都有且仅有一个映射值x t+1 。然而得到的混沌轨道看上去却非常随机——事实上逻辑斯蒂映射还被用来在计算机中生成伪随机数 。因此，表面上的随机可以来自非常简单的确定性系统。

此外，对于产生混沌的R值，如果初始条件x 0 有任何的不确定性，对一定时间之后的轨道就无法再预测了。R=4时我们已经看到这种状况。如果我们对x 0 不能精确到小数点后第10位——大多数实验观察都做不到这么精确——那么大约在t=30时，x t 的值就无法预测了。对于任何能产生混沌的R值，只要x 0 有不确定性，不管精确到小数点后多少位，最终都会在t大于某个值时变得无法预测。

数学生物学家梅对这些惊人的特性进行了总结，与庞加莱遥相呼应：

简单的确定性方程 （1）（即逻辑斯蒂映射）能产生类似于随机噪声的确定性轨道，这个事实有着让人困扰的实际含义。例如，这就意味着种群调查数据中那种明显的不稳定波动不一定表明环境的变化莫测或是采样有错误：它们有可能就是像方程（1）这样完全确定性的种群数量变化关系所导致的……另外，还可以看到，在混沌中，不管初始条件有多接近，在足够长的时间之后，它们的轨道还是会相互分开。这意味着，即使我们的模型很简单，所有的参数也都完全确定，长期预测也仍然是不可能的。

简而言之，系统存在混沌也就意味着，拉普拉斯式的完美预测不仅在实践中无法做到，在原则上也是不可能的，因为我们永远也无法知道x 0 小数点后的无穷多位数值。这是一个非常深刻的负面结论，它与量子力学一起，摧毁了19世纪以来的乐观心态——认为牛顿式宇宙就像钟表一样沿着可预测的路径运行。

但是对逻辑斯蒂映射的研究是不是也会产生一些正面作用呢？对于试图发现随时间变化的系统的一般原则的动力系统理论，它能有所助益吗？事实上，对逻辑斯蒂等映射的深入研究也已经得到了同样深刻的正面结果——从中发现了混沌系统的普遍特征。

混沌的共性

最早用术语混沌来描述对初始条件具有敏感依赖性的动力系统的人是物理学家李天岩（T.Y.Li）和约克（James Yorke）。 这个词用得恰到好处：在口语中“混沌”一词意指随机和不可预测，在逻辑斯蒂映射的混沌中就有这些性质。然而，与口语中的混沌不同，数学混沌还有本质上的秩序，即很多混沌系统所共有的普适性。

第一条普适性质：通往混沌的倍周期之路

在前面的数学探讨中，我们看到随着R从2.0增大到4.0，逻辑斯蒂迭代最初会产生不动点，然后是2周期振荡，然后是4周期，然后是8周期，一直下去，直到出现混沌。在动力系统理论中，这些突然的周期倍增被称为分叉（bifurcation）。不断分叉直至混沌的过程就是“通往混沌的倍周期之路”。

我们经常用分叉图来表现分叉，分叉图是“控制参数”（比如R）和系统吸引子之间的函数关系。图2.15就是逻辑斯蒂映射的分叉图。横坐标为R，纵坐标是各R值对应的x的最终值（吸引子）。例如，R=2.9时，x会到达固定点吸引子x=0.655。R=3.0时，x会到达双周期吸引子。这就是图中第一个分叉点，不动点吸引子换成了双周期吸引子。在3.4和3.5之间，又分叉为4周期吸引子，后面不断周期倍增，直至R到达3.569946附近，开始出现混沌的发端（onset of chaos）。

通往混沌的倍周期之路有着悠久的历史。 早在20世纪20年代，就在数学方程中发现了倍周期分叉，20世纪50年代芬兰数学家米尔堡（P.J.Myrberg）描述了类似的连续分叉。洛斯阿拉莫斯国家实验室的梅特罗波利斯、保罗·斯坦和米隆·斯坦证明，倍周期之路并不是只有逻辑斯蒂映射才有，事实上任何抛物线形状的映射都有类似现象。这里“抛物线形状”意指映射的图形有一个隆起——用数学术语说就是“单峰（unimodal）”。

第二条普适性质：费根鲍姆常数

到20世纪70年代，物理学家费根鲍姆（图2.16）的发现让倍周期之路得以在数学界闻名。费根鲍姆用一台可编程的台式计算器算出了倍周期分叉点的R值表（其中“≈”表示“约等于”）：

这里R 1 对应周期2 1 （=2），R 2对应周期2 2 （=4），R n 对应周期2 n 。符号∞（“无穷大”）用来标志混沌的出现——周期为无穷大的轨道。

费根鲍姆注意到，随着周期增大，R值之间的距离越来越近。这意味着随着R的增大，分叉之间的间隔越来越短。在图2.15的分叉图中可以看到这一点。费根鲍姆用这些R值计算了分叉靠近的速度，也就是R值的收敛速度。他发现速度约等于常数4.6692016。这意味着随着R值增加，新的周期倍增比前面的周期倍增出现的速度快大约4.6692016倍。

这很有趣，但还不至于让人震惊。当费根鲍姆研究了其他一些映射后——逻辑斯蒂只是研究过的映射之一——事情变得更有趣了。我在前面提到，在费根鲍姆进行这些计算之前的几年，他在洛斯阿拉莫斯的同事梅特罗波利斯、保罗·斯坦和米隆·斯坦就证明了所有单峰映射都会有类似的倍周期现象。费根鲍姆下一步做的就是计算其他单峰映射的收敛速度。他先算了正弦映射，正弦映射与逻辑斯蒂映射相似，不过用的是正弦函数。

费根鲍姆重复了前面的步骤：计算正弦映射的倍周期分叉点的R值，然后计算这些值的收敛速度。他发现收敛速度为4.6692016。

费根鲍姆很吃惊，速度是一样的。他又检验了其他单峰映射，结果还是一样。所有人，包括费根鲍姆自己，都根本没有想到会是这样。发现这个结果后，费根鲍姆接着又从理论上解释了为何常数4.6692016具有普适性——对所有单峰映射都成立。这个数现在被称为费根鲍姆常数。常数的理论解释使用了一种复杂的数学技巧——重正化（renormalization）。重正化最初是从量子力学中发展出来，后来又被应用到另一个物理学领域：相变和其他“临界现象”的研究。费根鲍姆将其引入了动力系统理论， 并成为理解混沌的基石。

后来发现这并不仅仅是数学现象。费根鲍姆做出这个发现之后，他的理论在多个物理动力系统的实验中得到了证实，包括流体、电路、激光和化学反应。在这些系统中都发现了倍周期分叉，也用类似的方法计算了费根鲍姆常数。在这些实验中很难准确测量分叉点的R值，但即使这样，实验得到的费根鲍姆常数也仍然在接近4.6692016的误差范围之内。这很让人印象深刻，因为费根鲍姆的理论在算出这个数时只涉及数学，没涉及物理。正如费根鲍姆的同事卡达诺夫（Leo Kadanoff）所说的，这是“一个科学家所能遇到的最好的事情， 头脑中想到的东西在自然界中得到了完美的印证”。

气象这样的大尺度的系统很难直接做实验，因此没有人在大尺度系统中直接观察到倍周期分叉或混沌。不过，一些气象计算机模型 却表现出了通往混沌的倍周期之路，另外电力系统、心脏、行星等系统的计算机模型中也有类似发现。

关于这个故事还有一件让人吃惊的事情。同许多重要的数学发现一样，几乎在费根鲍姆做出他的发现同时，另一个研究小组也独立发现了这个规律。这个小组是法国科学家科雷特（Pierre Coullet）和特雷瑟（Charles Tresser），他们也用重正化技术研究了倍周期分叉， 并且发现了单峰映射的普适常数4.6692016。费根鲍姆也许的确是第一个发现者，并且向科学界广泛而清晰地传播了这个结果，所以这个成就大部分被归功于他。不过在许多科技文献中，也称这个理论为“费根鲍姆—科雷特—特雷瑟理论”，称费根鲍姆常数为“费根鲍姆—科雷特—特雷瑟常数”。在书中还有几个这样的例子，都是在思想条件成熟时同时独立做出发现。

混沌思想带来的革命

在这一章我们看到，混沌的发现使得科学的许多核心原则被重新加以思考。这里我总结一下这些新思想，19世纪的科学家几乎没人会相信这些。

◆看似混沌的行为有可能来自确定性系统，无须外部的随机源。

◆一些简单的确定性系统的长期变化，由于对初始条件的敏感依赖性，即使在原则上也无法预测。

◆虽然混沌系统的具体变化无法预测，在大量混沌系统的普适共性中却有一些“混沌中的秩序”，例如通往混沌的倍周期之路，以及费根鲍姆常数。因此虽然在细节上“预测变得不可能”，但在更高的层面上混沌系统却是可以预测的。

总的来说，变化、难以预测的宏观行为是复杂系统的标志。动力系统理论为刻画其行为提供了数学词汇表，例如分叉、吸引子以及系统变化方式的普适特性。这些词汇在复杂系统的研究中频繁出现。

逻辑斯蒂映射是种群数量增长的简化模型，但是对其以及类似模型的详细研究却带来了对秩序、随机和可预测性的重新认识。这证明了理想模型（idea models）的力量——这些模型很简单，用数学或计算机就足以进行研究，但是又抓住了自然界复杂系统的本质。理想模型在这本书中，乃至整个复杂系统科学中都扮演了重要角色。

刻画复杂系统的动力学还只是理解它的第一步。我们还要理解这些动力系统如何被用在生命系统中以处理信息和适应环境变化。后三章会针对这些主题给出一些背景知识，然后我们再来看看从动力学中得到的思想如何与信息论、计算和进化结合起来。

[19] “这是一个线性系统”：有人可能会说这个并不真的是线性系统，因为群体数量随时间呈指数增长：n t =2 t n 0 。不过这里的线性指的是n t 到n t+1 是线性映射。

[21] “我不给出逻辑斯蒂模型的具体形式”：逻辑斯蒂模型如下： 其中n t 是当前这一代的种群数量，k是承载能力。让x t =n t /k, R=（出生率-死亡率），就能从中得到逻辑斯蒂映射。其中x t 表示“承载率”：当前种群数量与最大可能的种群数量的比率。从而 因为种群数量n t 总是介于0和k之间，所以x t 总是介于0和1之间。 XDZg9PLV81zzWKJDMXtjGK9VdzmIxr4By6SoT3iy4f34hxW39qlyNCsiJeLB12h8