




“凑整法”是在计算过程当中,将中间步骤中的某些数字凑成一个“整数”(整十、整百、整千等方便计算的数字),从而简化计算。
比如我们在计算56×99等于几的时候,很多人觉得无法通过口算计算出结果,其实如果我们运用凑整法就会很简单,即把它变成56×(100-1)就行了。
凑整法是简便运算中最常用的一种计算方法,在具体计算时,除了在过程中凑整,我们还可以综合运用数字运算的交换律、结合律等,把可以凑成整十、整百、整千等计算起来更加方便的数放在一起先行运算,从而提高运算速度。
运用凑整法,最重要的是观察数字的特征,判断哪些数字可以凑整,然后应用相关的定律和性质进行运算,通常能够化繁为简。可以运用凑整法的数学运算题目一般有以下几种。
①加法“凑整”。利用加法的交换律、结合律“凑整”。如:
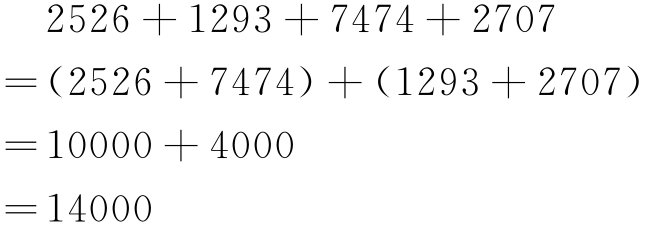
②减法“凑整”。利用减法性质“凑整”。如:
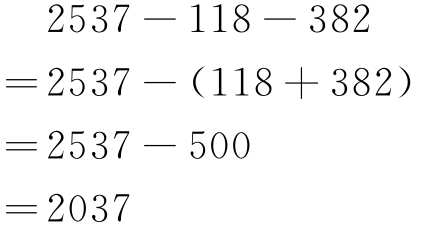
③乘法“凑整”。利用乘法交换律、结合律、分配律“凑整”。如:
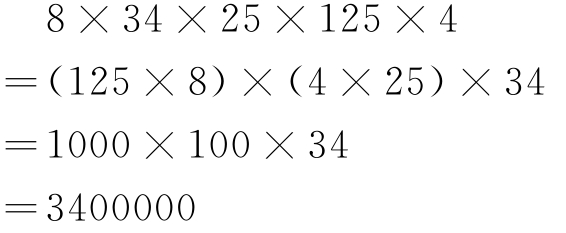
④和(差)代替“凑整”。利用和或差代替原数进行“凑整”。
如126、99、102等,我们可以用(125+1)、(100-1)、(100+2)等来代替,使运算变得比较简便、快速。
要想能够快速准确地判断和学习凑整法,我们需要记住一些最基本的凑整算式:
5×2=10
25×4=100
25×8=200
25×16=400
125×4=500
125×8=1000
125×16=2000
625×4=2500
625×8=5000
625×16=10000
…
记住这些常见的凑整算式,我们就可以在运用凑整法计算题目时更加得心应手了。
方法 :
A ×5型式子的速算技巧: A ×5=10 A ÷2。
A ×25型式子的速算技巧: A ×25=100 A ÷4。
A ×125型式子的速算技巧: A ×125=1000 A ÷8。
提示 : A 为变量,代表任意数 。
例子 :
(1)计算8739.45×5= 。
解 :
10×8739.45÷2
所以8739.45×5=43697.25。
(2)计算7234×25= 。
解 :
7234×100÷4
所以7234×25=180850。
(3)计算8736×125= 。
解 :
8736×1000÷8
所以8736×125=1092000。
练习 :
(1)计算36.843×5= 。
(2)计算3714×25= 。
(3)计算4115×125= 。
方法 :
(1)被乘数除以2(如除不尽则取整数部分)。
(2)被乘数是单数则补5,双数则补0。
(3)将上步结果乘以11。
例子 :
(1)计算37×55= 。
解 :
37÷2=18
因为37是单数,后面补5为185。
185×11=2035
所以 37×55=2035
(2)计算32×55= 。
解 :
32÷2=16
因为32是双数,后面补0为160。
160×11=1760
所以 32×55=1760
(3)计算78×55= 。
解 :
78÷2=39
因为78是双数,后面补0为390。
390×11=4290
所以 78×55=4290
练习 :
(1)计算178×55= 。
(2)计算97×55= 。
(3)计算26×55= 。
方法 :
(1)先把5的奇数倍乘以2。
(2)与另一个乘数相乘。
(3)结果除以2。
例子 :
(1)计算28×5= 。
解 :
5×2=10
28×10=280
280÷2=140
所以 28×5=140
(2)计算98×15= 。
解 :
15×2=30
98×30=2940
2940÷2=1470
所以 98×15=1470
(3)计算59×25= 。
解 :
25×2=50
59×50=2950
2950÷2=1475
所以 59×25=1475
练习 :
(1)计算88×35= 。
(2)计算42×15= 。
(3)计算59×45= 。
方法 :
(1)用被乘数加上自己的一半(如得出数有小数则省略小数部分)。
(2)奇数后面补5,偶数后面补0。
例子 :
(1)计算44×15= 。
解 :
44+44÷2=66
44是双数,补0,所以结果为660。
所以 44×15=660
(2)计算33×15= 。
解 :
33+33÷2=49.5省略小数部分为49。
33是单数,补5,所以结果为495。
所以 33×15=495
(3)计算125×15= 。
解 :
125+125÷2=125+62=187
125是单数,补5,所以结果为1875。
所以 125×15=1875
练习 :
(1)计算76×15= 。
(2)计算144×15= 。
(3)计算257×15= 。
方法 :
A ×1.5= A + A ÷2
例子 :
(1)计算1944×1.5= 。
解 :
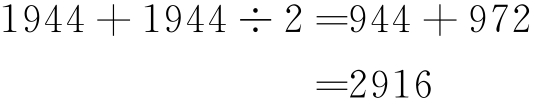
所以 1944×1.5=2916
(2)计算98×1.5= 。
解 :
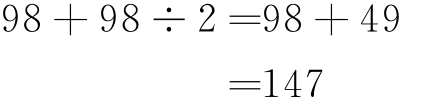
所以 98×1.5=147
(3)计算125×1.5= 。
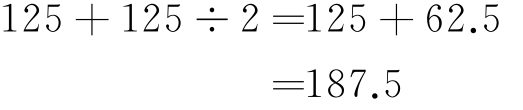
所以 125×1.5=187.5
练习 :
(1)计算76×1.5= 。
(2)计算144×1.5= 。
(3)计算257×1.5= 。
在美国,很多餐馆是需要支付小费的,一般是消费金额的15%,那么,我们怎样快速地计算出该给多少小费呢?
方法 :
(1)先计算消费金额的10%,也就是1/10。
(2)将上一步的结果除以2。
(3)将前两步的结果相加。
例子 :
(1)计算44×15%= 。
解 :
44×10%=4.4
4.4÷2=2.2
4.4+2.2=6.6
所以 44×15%=6.6
(2)计算98×15%= 。
解 :
98×10%=9.8
9.8÷2=4.9
9.8+4.9=14.7
所以 98×15%=14.7
(3)计算125×15%= 。
解 :
125×10%=12.5
12.5÷2=6.25
12.5+6.25=18.75
所以 125×15%=18.75
练习 :
(1)计算76×15%= 。
(2)计算144×15%= 。
(3)计算257×15%= 。
方法 :
(1)两个乘数的个位上的5相乘得到25。
(2)十位相乘时应按 N ×( N +1)的方法进行,得到的积直接写在25的前面。
例如 a 5× a 5,则先得到25,然后计算 a ×( a +1)并放在25前面即可。
例子 :
(1)计算35×35= 。
解 :
5×5=25
3×(3+1)=12
所以 35×35=1225
(2)计算85×85= 。
解 :
5×5=25
8×(8+1)=72
所以 85×85=7225
(3)计算95×95= 。
解 :
5×5=25
9×(9+1)=90
所以 95×95=9025
注意 : 本题运用的方法不是凑整法,之所以放在这里讲,是因为它是后面几种题型的基础 。
练习 :
(1)计算15 2 = 。
(2)计算25 2 = 。
(3)计算45 2 = 。
我们知道尾数为5的两个两位数的平方的计算方法,现在我们来学习尾数为6的两位数的平方算法。
方法 :
(1)先算出这个数减1的平方数。
(2)算出这个数与比这个数小1的数的和。
(3)将前两步的结果相加。
例子 :
(1)计算76 2 = 。
解 :
75 2 =5625
76+75=151
5625+151=5776
所以 76 2 =5776
(2)计算16 2 = 。
解 :
15 2 =225
16+15=31
225+31=256
所以 16 2 =256
(3)计算96 2 = 。
解 :
95 2 =9025
96+95=191
9025+191=9216
所以 96 2 =9216
练习 :
(1)计算26 2 = 。
(2)计算46 2 = 。
(3)计算56 2 = 。
方法 :
(1)先算出这个数减2的平方数。
(2)算出这个数与比这个数小2的数的和的2倍。
(3)将前两步的结果相加。
例子 :
(1)计算87 2 = 。
解 :
85 2 =7225
(87+85)×2=344
7225+344=7569
所以 87 2 =7569
(2)计算27 2 = 。
解 :
25 2 =625
(27+25)×2=104
625+104=729
所以 27 2 =729
(3)计算57 2 = 。
解 :
55 2 =3025
(57+55)×2=224
3025+224=3249
所以 57 2 =3249
扩展阅读
相邻两个自然数的平方之差是多少?学过平方差公式的同学们应该很容易就可以回答出这个问题 。
b 2 - a 2 =( b + a )( b - a )
所以差为1的两个自然数的平方差为 :
( a +1) 2 - a 2 =( a +1)+ a
差为2的两个自然数的平方差为 :
( a +2) 2 - a 2 =[( a +2)+ a ]×2
同理,差为3的两个自然数的平方差也可以计算出来 。
练习 :
(1)计算17 2 = 。
(2)计算37 2 = 。
(3)计算77 2 = 。
方法 :
(1)先凑整算出这个数加2的平方数。
(2)算出这个数与比这个数大2的数的和的2倍。
(3)将前两步的结果相减。
例子 :
(1)计算78 2 = 。
解 :
80 2 =6400
(78+80)×2=316
6400-316=6084
所以 78 2 =6084
(2)计算28 2 = 。
解 :
30 2 =900
(28+30)×2=116
900-116=784
所以 28 2 =784
(3)计算58 2 = 。
解 :
60 2 =3600
(58+60)×2=236
3600-236=3364
所以 58 2 =3364
扩展阅读
尾数为1、2、3、4的两位数的平方数与上面这种方法相似,只需找到相应的尾数为5或者尾数为0的整数即可 。
另外不止两位数适用本方法,其他的多位数平方同样适用 。
练习 :
(1)计算28 2 = 。
(2)计算38 2 = 。
(3)计算98 2 = 。
方法 :
(1)先凑整算出这个数加1的平方数。
(2)算出这个数与比这个数大1的数的和。
(3)将前两步的结果相减。
例子 :
(1)计算79 2 = 。
解 :
80 2 =6400
79+80=159
6400-159=6241
所以 79 2 =6241
(2)计算19 2 = 。
解 :
20 2 =400
19+20=39
400-39=361
所以 19 2 =361
(3)计算59 2 = 。
解 :
60 2 =3600
59+60=119
3600-119=3481
所以 59 2 =3481
练习 :
(1)计算29 2 = 。
(2)计算39 2 = 。
(3)计算99 2 = 。
方法 :
(1)底数的十位数乘以十位数(即十位数的平方)。
(2)底数的十位数加十位数(即十位数乘以2)。
(3)将前两步的结果相加后再加1。
例子 :
(1)计算71 2 = 。
解 :
70×70=4900
70×2=140
所以 71 2 =4900+140+1=5041
(2)计算91 2 = 。
解 :
90×90=8100
90×2=180
所以 91 2 =8100+180+1=8281
提示 : 熟悉之后,也可以省掉后面的0进行速算 。
解 :
9×9=81
9×2=18
所以 91 2 =8281
(3)计算31 2 = 。
解 :
30×30=900
30×2=60
所以 31 2 =900+60+1=961
注意 : 可参阅乘法速算中的“尾数是1的两位数相乘”的内容 。
练习 :
(1)计算81 2 = 。
(2)计算61 2 = 。
(3)计算21 2 = 。
方法 :
方法一:除数增加两倍,结果再乘以2,即为商。
方法二:被除数除以10。再乘以2,即为商。
方法三:被除数乘以2,结果再除以10。
例子 :
(1)计算46÷5= 。
解 :
将除数乘以2以后,
算式变为46÷10,
结果是4.6。
再乘以2。
所以 46÷5=4.6×2=9.2
(2)计算13÷5= 。
解 :
将被除数除以10,
即13÷10,
结果是1.3。
再乘以2。
所以 13÷5=1.3×2=2.6
(3)计算95÷5= 。
解 :
将被除数除以10,
即95×2,
结果是190。
再除以10。
所以 95÷5=95×2÷10=19
练习 :
(1)计算1024÷5= 。
(2)计算569÷5= 。
(3)计算1111÷5= 。
我们学过,如果被除数和除数同时乘以或除以一个相同的数(这个数不等于零),那么所得的商不变。这就是商不变的性质。根据这个性质,可以使一些除法算式计算简便。
方法 :
将被除数和除数同时乘以一个数,使得除数变成容易计算的数字。
例子 :
(1)计算2436÷5= 。
解 :
将被除数和除数同时乘以2,
算式变为4872÷10,
结果是487.2。
所以 2436÷5=487.2
(2)计算1324÷25= 。
解 :
将被除数和除数同时乘以4,
算式变为5296÷100,
结果是52.96。
所以 1324÷25=52.96
(3)计算10625÷625= 。
解 :
将被除数和除数同时乘以16,
算式变为170000÷10000,
结果是17。
所以 10625÷625=17
练习 :
(1)计算3024÷15= 。
(2)计算8569÷25= 。
(3)计算1111÷55= 。
我们学过乘法交换律。交换因数的位置积不变。在连除式题中也同样可以交换除数的位置,商不变。
所以,在连除运算中有这样的性质:一个数除以另一个数所得的商,再除以第三个数,等于第一个数除以第三个数所得的商,再除以第二个数。
用字母表示为:
a ÷ b ÷ c = a ÷ c ÷ b
另外,在连除运算中,还可以利用添括号的方法来进行速算和巧算。
在连除算式中,一个数除以另一个数所得的商再除以第三个数,等于第一个数除以第二、三两个数的积。即添上括号后,因为括号前面是除号,所以括号中的运算符号要变为乘号。
用字母表示为:
a ÷ b ÷ c = a ÷( b × c )
利用这个法则可以把两个除数相乘。如果积是整十、整百、整千,则可以使计算简便。
利用这两个性质可以使连除运算简便。
方法 :
(1) a ÷ b ÷ c = a ÷ c ÷ b
(2) a ÷ b ÷ c = a ÷( b × c )
例子 :
(1)计算45000÷125÷15= 。
解 :
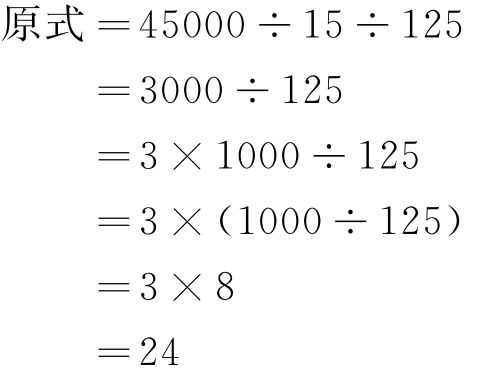
所以 45000÷125÷15=24
(2)计算4900÷4÷25= 。
解 :
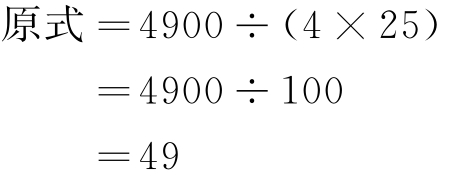
所以 4900÷4÷25=49
(3)24024÷4÷6= 。
解 :
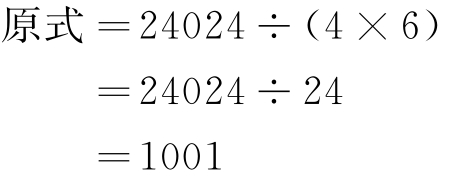
所以 24024÷4÷6=1001
练习 :
(1)计算5000÷8÷125= 。
(2)计算7000÷25÷35= 。
(3)计算147000÷16÷625= 。
在乘除混合运算中,可以把乘数、除数带符号“搬家”。也可以“去括号”或“添括号”。当“去的括号”(或“添的括号”)前面是乘号时,则“要去的括号”(或“要添的括号”)内运算符号不变;当“要去的括号”(或“要添的括号”)前面是除号时,则“要去的括号”(或“要添的括号”)内运算符号要改变。原来乘号变为除号,原来的除号变为乘号。用字母表示为(从左往右看是添括号,从右往左看是去括号):
a × b ÷ c = a ÷ c × b = a ×( b ÷ c )
a ÷ b × c = a ÷( b ÷ c )
a ÷( b × c )= a ÷ b ÷ c
利用以上乘除混合运算性质,可以使计算简便。
方法 :
(1) a × b ÷ c = a ÷ c × b = a ×( b ÷ c )
(2) a ÷ b × c = a ÷( b ÷ c )
(3) a ÷( b × c )= a ÷ b ÷ c
例子 :
(1)计算150×40÷50= 。
解 :
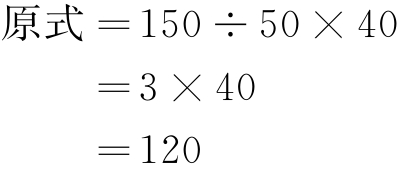
所以 150×40÷50=120
(2)计算1320×500÷250= 。
解 :
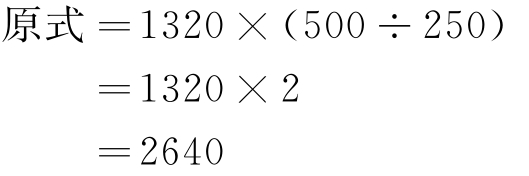
所以 1320×500÷250=2640
(3)计算72000÷(125×9)= 。
解 :
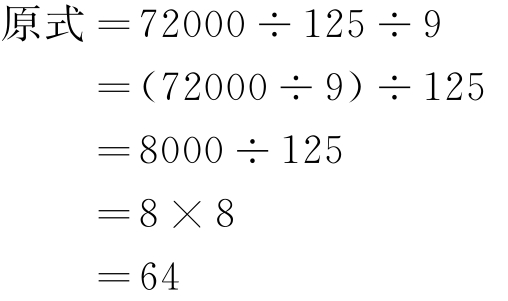
所以 72000÷(125×9)=64
练习 :
(1)计算864×27÷54= 。
(2)计算1320×500÷250= 。
(3)计算372÷162×54= 。
方法 :
(1)在两个加数中选择一个数,加上或减去一个数,使它变成一个末尾是0的数。
(2)同时,在另一个数中,相应地减去或加上这个数。
口诀:一边加,一边减。
例子 :
(1)计算297+514= 。
解 :
297差3到300,则:
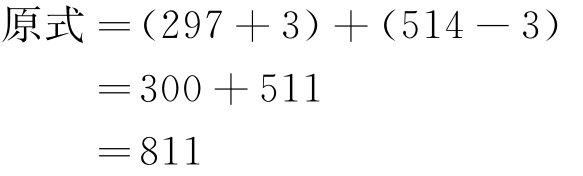
所以 297+514=811
(2)计算308+194= 。
解 :
308比300多8,则:
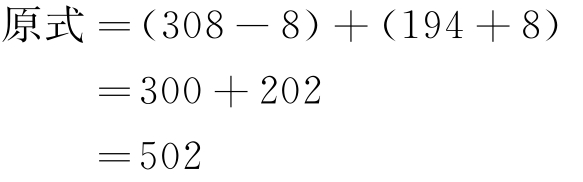
所以 308+194=502
(3)计算2991+1452= 。
解 :
2991差9到3000,则:
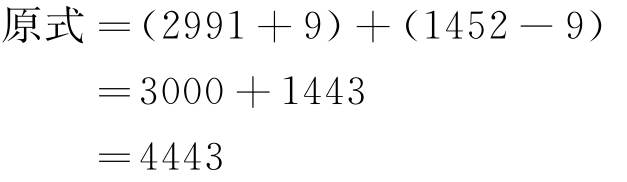
所以 2991+1452=4443
注意 : 两个加数要一边加、一边减,才能保证结果不变 。
练习 :
(1)计算902+681= 。
(2)计算497+362= 。
(3)计算4198+2629= 。
方法 :
将被减数和减数同时加上或者同时减去一个数,使得减数成为一个整数,从而方便计算。
口诀:同加或同减。
例子 :
(1)计算85-21= 。
解 :
首先将被减数和减数同时减去1。
即被减数变为85-1=84
减数变为21-1=20
则84-20=64
所以 85-21=64
(2)计算458-195= 。
解 :
首先将被减数和减数同时加上5。
即被减数变为 458+5=463
减数变为 195+5=200
则 463-200=263
所以 458-195=263
(3)计算2816-911= 。
解 :
首先将被减数和减数同时减去11。
即被减数变为2816-11=2805
减数变为911-11=900
则2805-900=1905
所以 2816-911=1905
练习 :
(1)计算4582-495= 。
(2)计算9458-2104= 。
(3)计算8458-2014= 。
凑整法是小数加减法速算与巧算运用的主要方法。
方法 :
(1)用的时候看小数部分,主要看末位。
(2)需要注意的是,小数点一定要对齐。
例子 :
(1)计算5.6+2.38+4.4+0.62= 。
解 :
5.6与4.4刚好凑成10,2.38与0.62刚好凑成3。所以:
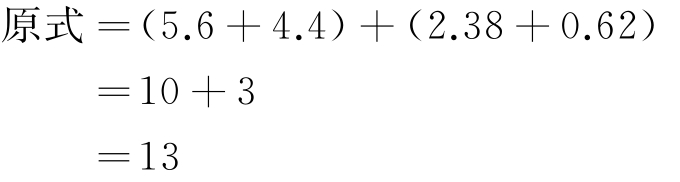
所以 5.6+2.38+4.4+0.62=13
(2)计算1.999+19.99+199.9+1999= 。
解 :
因为小数计算起来容易出错。刚好1999接近整千数2000,其余各加数看作与它接近的容易计算的整数。再把多加的那部分减去。所以:
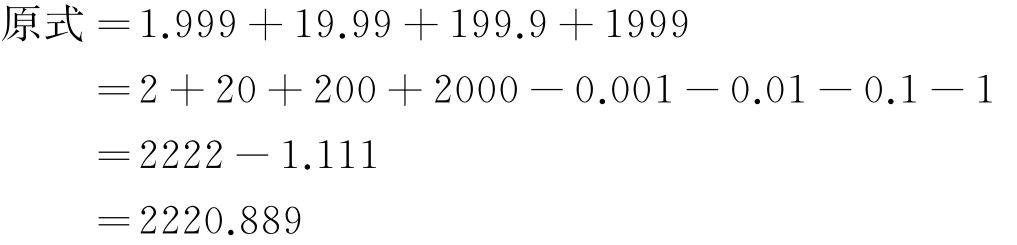
所以 1.999+19.99+199.9+1999=2220.889
注意 : 一定要记住刚才“多加的”要“减掉”,“多减的”要“加上 ”。
(3)计算34.16+47.82+53.84+64.18= 。
解 :
这是一个“聚10”相加法的典型例题,所谓“聚10”相加法,即当有几个数字相加时,利用加法的交换律与结合律,将加数中能聚成10或10的倍数的加数交换顺序,先进行结合,然后再把一些加数相加,得出结果。或者改变运算顺序,将相加得整十、整百、整千的数先结合相加,再与其他数相加,得出结果。这是一种运用非常普遍的巧算方法。
这道题目中四个数字都是由整数部分和小数部分组成。因而可以将此题分成整数部分和小数部分两部分来考虑。若只看整数部分,第二个数与第三个数之和正好是100,第一个数与第四个数之和正好是98;再看小数部分,第一个数的0.16与第三个数的0.84的和正好为1,第二个数的0.82与第四个数的0.18之和也正好为1。因此,总和是整数部分加上小数部分,即
原式=100+98+1+1=200
练习 :
(1)计算13.6+25.38+16.4+14.62= 。
(2)计算9.8+99.88+999.888+9999.8888= 。
(3)计算53.64+55.78+16.44+54.56+14.22+16.36= 。
与整数运算中的“凑整法”相同,在分数运算中,充分利用四则运算法则和运算律(如交换律、结合律、分配律),使部分的和、差、积、商成为整数、整十数……可以使分数运算得到简化。
方法 :
(1)充分运用四则运算法则和运算律。
(2)先借后还。
例子 :
(1)计算
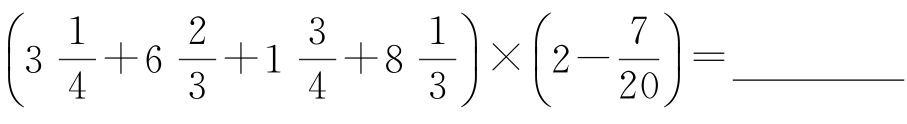 。
。
解 :
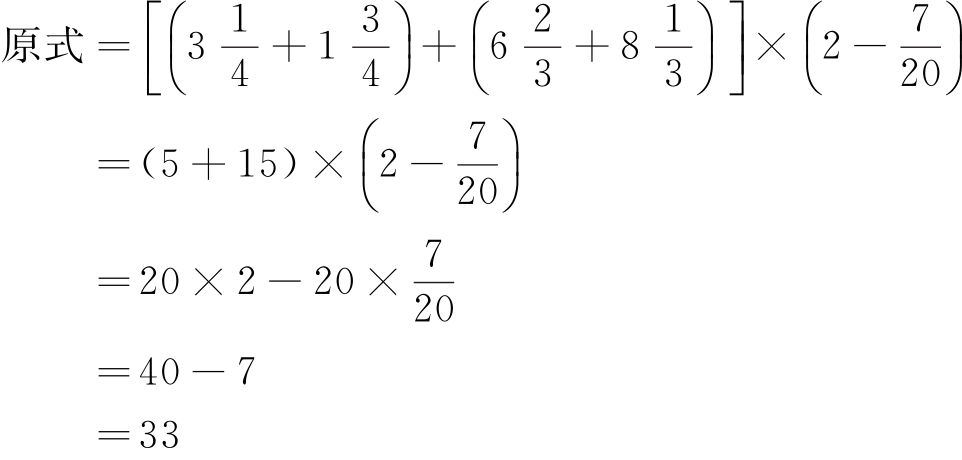
所以
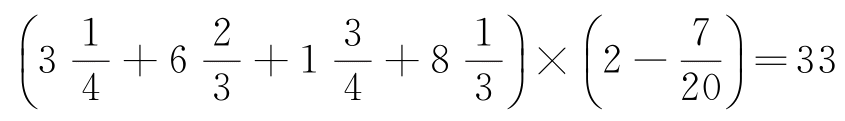
(2)计算
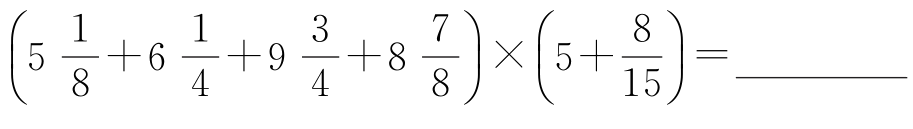 。
。
解 :
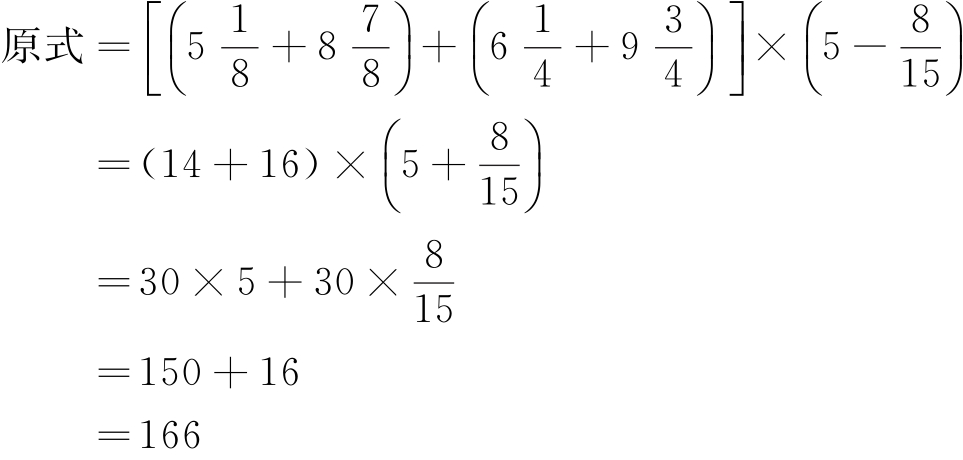
所以
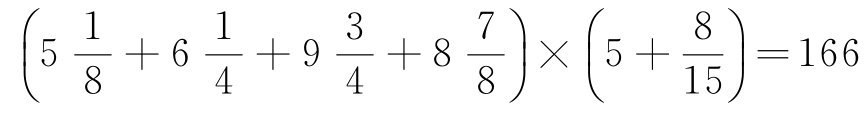
(3)计算
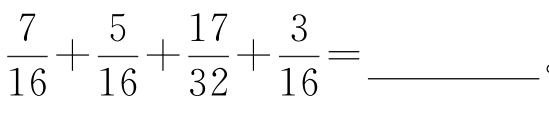 。
。
解 :
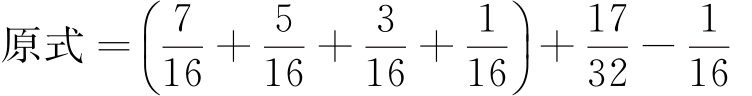
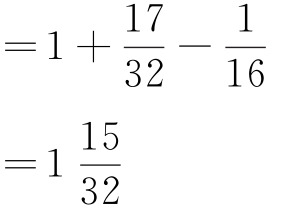
所以
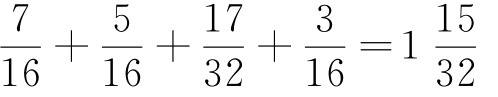
练习 :
(1)计算
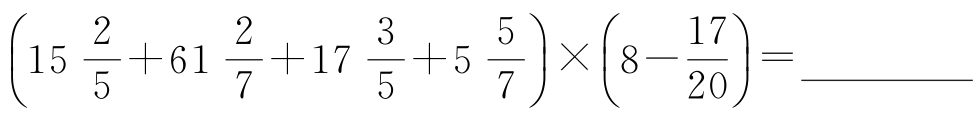 。
。
(2)计算
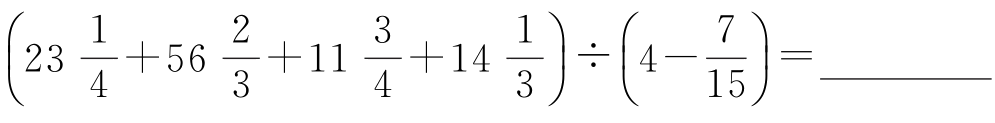 。
。
(3)计算
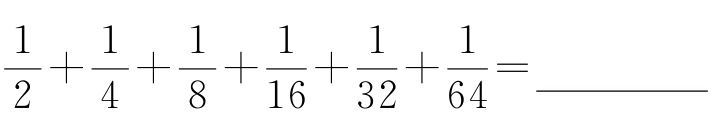 。
。