





§5.1
[5.1]
还应提到的三角函数有cotθ=cosθ/sinθ=(tanθ)
-1
,secθ=(cosθ)
-1
和cosecθ=(sinθ)
-1
。还有“双曲”函数sinh
t
=
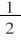 (e
t
-e
-
t
),cosh
t
=
(e
t
-e
-
t
),cosh
t
=
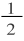 (e
t
+e
-
t
),tanh
t
=sinh
t
/cosh
t
,等等。注意,这些函数的反函数记为cot
-1
,sinh
-1
,等等,就像§5.1里的“tan
-1
(
y
/
x
)”那样。
(e
t
+e
-
t
),tanh
t
=sinh
t
/cosh
t
,等等。注意,这些函数的反函数记为cot
-1
,sinh
-1
,等等,就像§5.1里的“tan
-1
(
y
/
x
)”那样。
§5.2
[5.2] 对数是由纳皮尔(John Napier,1550~1617)于1614年引入的,1624年,布里格斯(Henry Briggs,1561~1630)将其推广应用。
§5.3
[5.3] 自然对数通常也作“ln”。
[5.4] 从迄今所建立起来的情况看,我们不能推断说公式 z =log r +iθ中的“iθ”不可是iθ的实数倍。这需要计算。
[5.5] 柯茨(Cotes,1714)得到过等价的公式log(cosθ+i sinθ)=iθ,欧拉的e iθ =cosθ+i sinθ第一次出现时似乎要比前者晚了30年(见Euler,1748)。
[5.6] 这里对(cosθ) 3 我用的是方便(但有些不合逻辑)的记法cos 3 θ。而记号cos -1 θ通常则用以表示反函数arccosθ。公式sin n θ+i cos n θ=(sinθ+i cosθ) n 有时也称为“棣莫弗(De Moivre)定理”。亚伯拉罕·棣莫弗作为与罗杰·柯茨同时代的人,似乎也是e iθ =sinθ+i cosθ的共同发现者之一。
**〔5.1〕 检验这些不同的可能性。
**〔5.2〕 不妨试试。
***〔5.3〕 试不做具体计算也不用三角学来验证这一点。( 提示 :这是“分配律” w ( z 1 + z 2 )= wz 1 + wz 2 的结果,它说明复平面保“线性”结构,而 w (i z )=i( wz )则说明转过一个直角的转动是保角的,即直角在转动中保持不变。)
*〔5.4〕 验证这一点。
***〔5.5〕 直接从级数验证这一点。( 提示 :按照整数指数的“二项式定理”,( a + b ) n 的 a p b q 项的系数为 n !/ p ! q !。)
*〔5.6〕 由此证明 z +πi是- w 的对数。
*〔5.7〕 验证一下
*〔5.8〕 验证一下。
***〔5.9〕 证明这一点。可有多少种方法?找出所有特解。
**〔5.10〕 解这个“疑难”:因为e=e 1+2πi ,故e=(e 1+2πi ) 1+2πi =e 1+4πi-4π2 =e 1-4π2 。
*〔5.11〕 证明这一点。
*〔5.12〕 为什么这是一种容许的规定?
*〔5.13〕 证明为什么这是有效的。
*〔5.14〕 验证这一点。
**〔5.15〕 证明这一点。