





请看图2.11。它是一幅埃舍尔(M. C. Escher,1898~1972)木刻画《圆极限I》的复制品。这幅作品为我们提供了对一种几何——所谓双曲几何(也称为 罗巴切夫斯基 [Lobachevsky] 几何 )——的非常精确的表示。在这种几何下,平行公设不成立,毕达哥拉斯定理也不成立,三角形的内角和不等于π。而且,对给定的大小的形状,一般不存在同等大小的相似形。
在图2.11中,埃舍尔用了一种特定的双曲几何表示,其中整个双曲平面“世界”被“挤压”到普通欧几里得平面上圆的内部。这个边界圆表示这个双曲世界的“无穷远”。在埃舍尔的画中我们可以看到,处于边界圆附近的鱼非常拥挤。但我们应当意识到,这是一种假象。想象一下,假如你是一条这样的鱼,那么不论你处于埃舍尔画的边缘还是处于它的中心,整个(双曲)世界对你来说不会两样。这种几何里的“距离”概念与欧几里得平面的距离概念不同。由于我们是从欧几里得几何的视角来看埃舍尔画的,因此接近边界圆的鱼才会看上去显得微小。但从白鱼和黑鱼本身的“双曲”几何视角上看,它们认为它们与处于中心的那些弟兄们无论大小还是形状都并无二致。另外,虽然从我们外在的欧几里得几何观点看,它们似乎越接近边界圆越挤,但从它们自己的双曲观点角度上看,边界总是在无穷远。对他们来说,既不存在边界圆,也不存在在它们之外的“欧几里得”空间。它们的整个世界是由在我们看来严格处于圆内的那些东西组成的。
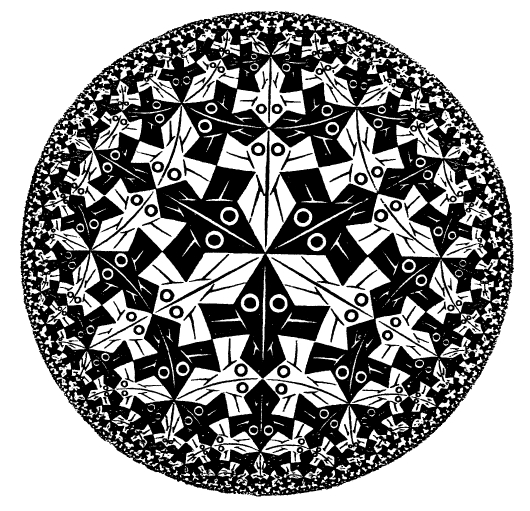
图2.11 埃舍尔的木刻画《圆极限I》。它展示了双曲几何的共形表示。
用更数学化的语言来说,这种双曲几何图像是如何构造的?考虑欧几里得平面上任意一个圆。处于这个圆内部的点集代表着整个双曲平面上的点集。双曲几何的直线表现为与边界圆 垂直 相交的欧几里得圆的一段。可以证明,双曲几何里任意相交的两条曲线在交点处的 角 精确等于欧几里得几何下测得的两曲线在交点处的角。这种性质的表示称为 共形表示 。正是由于这一点,埃舍尔所用的双曲几何的这种特殊表示有时被称为双曲平面的 共形模型 。(经常也称它为 庞加莱圆盘 。这一术语的历史渊源将在§2.6讨论。)
现在我们可以看看在双曲几何里三角形的内角和是不是等于π了。从图2.12一望便知这是不对的,三角形的内角和要小于π。我们或许会认为这是双曲几何不令人满意的地方,因为对三角形的内角和我们似乎得不到一个“简洁的”答案。但是我们可以从双曲三角形的内角和得到另一个特别优美和值得注意的结果。具体地说,如果三角形的三个角分别为α,β和γ,则我们有公式(由兰伯特(Johann Heinrich Lambert,1728~1777)发现):
π-(α+β+γ)= C Δ,
这里Δ是三角形的面积, C 是某个常数。这个常数的选取依赖于所测长度和面积所用的“单位”。通常我们总是取 C =1。在双曲几何下,三角形的面积可以如此简单地表达,这确实是一个非比寻常的事实。在欧几里得几何里,三角形的面积不可能简单地根据它的角表示出来,而是相当复杂地取决于其边长。
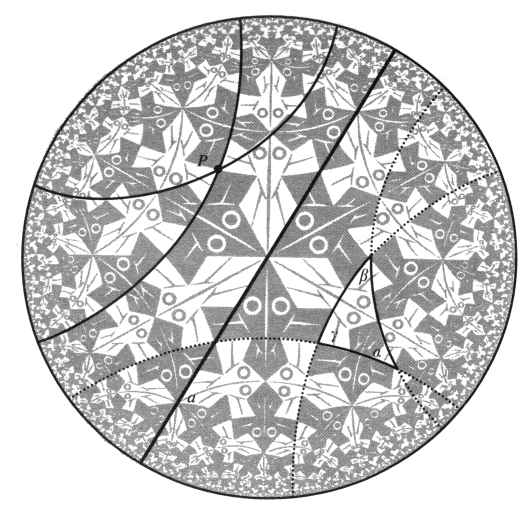
图2.12 与图2.11相同的埃舍尔的作品,只是图中加入了双曲直线(与边界圆垂直相交的欧几里得圆或线)和一个双曲三角形。双曲角等于欧几里得角。平行公设在此显然不成立,三角形的内角和小于π。
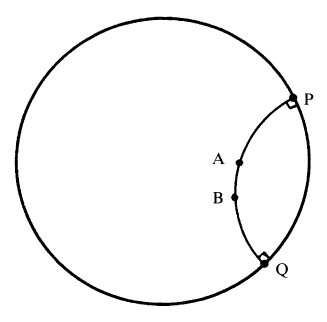
图2.13 在共形表示中,A和B之间的双曲距离是log{QA·PB/QB·PA},其中QA等是欧几里得距离,P和Q是过A和B的与边界圆(双曲直线)垂直的欧几里得圆与边界圆的交点。
实际上,共形表示下的双曲几何内容远不止这一点,我还没有描述两点间的双曲几何距离是如何定义的(在能够真正讨论面积之前,我们有必要搞清楚什么是“距离”)。这里我直接给出圆上两点 A 和 B 之间的双曲距离表达式:
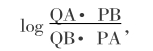
这里,P和Q是过点A和B且垂直于边界圆的欧几里得圆(即双曲直线)与边界圆的交点,“QA”等是欧几里得距离(见图2.13)。如果要在兰伯特面积公式里出现 C (即 C ≠1),我们只要将上述距离公式乘以 C -1/2 即可( C 的平方根的倒数)。 [4] , **〔2.2〕 后面我会更清楚地说明,这个量 C -1/2 指的是这种几何的 伪半径 。
如果你对这种带“log”的数学表达式感到为难,不必着急。这种公式只是为那些想更清楚地了解这一问题的人准备的。我不打算解释为什么表达式会是这个样子(例如,为什么按这种方式定义的两点间的最短双曲距离实际是沿双曲直线来量度的,还有为什么沿双曲直线测得的距离可以适当地“相加”,等等)。 *〔2.3〕 对“log”(对数)的使用我也要说声抱歉,我只能说事实就是如此。实际上,这里的对数是指 自然对数 (“以e为底的对数”),我将在§§5.2,3予以详细介绍。我们会发现,对数真的是非常漂亮和神秘(就像e一样),同时在许多方面也非常重要。
可以证明,这种距离定义下的双曲几何具有欧几里得几何中除了与平行公设有关的那些性质之外的所有其他性质。我们可以有三角形和其他不同形状和大小的平面图形,可以在与欧几里得几何同样多的自由度下“刚性地”(保持其双曲形状和大小不变)移动这些图形,因此,像欧几里得情形下一样,所谓两个图形出现“全等”,指的是它们“可通过刚性移动使二者完全重合”。按照这种双曲几何,埃舍尔木刻画中的所有白鱼是彼此全等的,所有黑鱼亦如此。