




本章分析的最优化问题不牵涉时点的变化,讨论的只是单个时点的最优化问题,即静态最优化问题。
考虑下述问题:
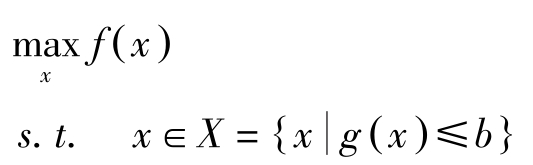
其中, f ( x )为目标函数, f 为 R n → R 的映射, x =( x 1 , x 2 ,…, x n )为商品的投入向量,投入 x 需消耗 g ( x )数量的资源, g 为 R n → R m 的映射, b 为资源总量。
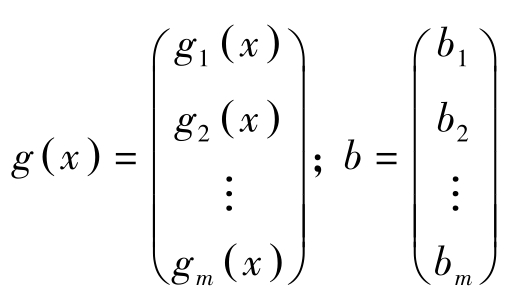
先不考虑约束条件,假定 g ( x )存在最优解 x ∗ 。下面分三种情况讨论该问题的求解:
(1)约束未起作用,即 g ( x ∗ )< b ;
(2)约束取等号,即 g ( x ∗ )= b ;
(3)有些约束未起作用,有些取等号,即 g ( x ∗ )≤ b 。
在约束未起作用的场合, g ( x ∗ )< b , x ∗ 在 X 的内部,相当于无约束的情况。
在古典方法中,让 x 在最优解 x ∗ 的周围发生微小变动Δ x ,看一下函数值的变化。若 f ( x )在 x ∗ 及其附近连续可微,则忽略高阶小量有:
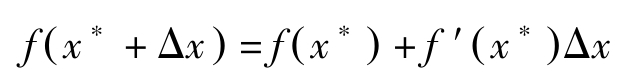
由于 x ∗ 是最大解, f ( x ∗ )≥ f ( x ∗ +Δ x ),因此 f ( x ∗ )≥ f ( x ∗ )+ f′ ( x ∗ )Δ x ,即
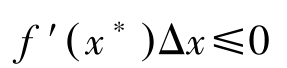
但Δ x 可正可负,因此必有 f′ ( x ∗ )=0。
于是我们有:
定理1: f 在 R n 上连续可微,若存在 x ∗ 使得 g ( x ∗ )< b ,那么 x ∗ 为上述问题最优解的一阶必要条件是 f′ ( x ∗ )=0。此时, x ∗ 为内点解。
下面的定理2给出 x ∗ 为极大值的一个充分条件。
定理2: f 为 R n 上连续可微凹函数,若 g ( x ∗ )< b 且 f′ ( x ∗ )=0,则 x ∗ 为极大值点。
证明: 因 f 是凹函数,所以有: f ( x ) -f ( x ∗ )≤ f′ ( x ∗ )( x-x ∗ )。又 f′ ( x ∗ )=0,故 f ( x ∗ )≥ f ( x ),即 x ∗ 为极大值点。
定理3(包络定理): 假定 f 在( R n )上连续可微,且 x ∗ ( a )为下述问题
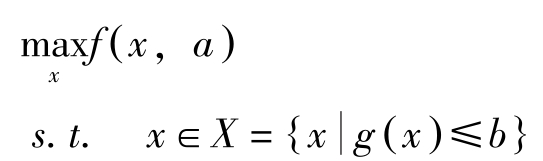
的最优解。记
f
∗
(
a
)≡
f
[
x
∗
(
a
),
a
],若
x
∗
(
a
)在
X
的内部且关于
a
连续可微,那么
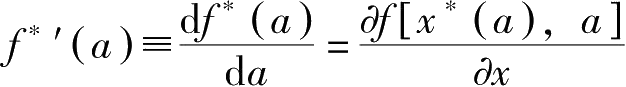 成立。
成立。
证明:
因
x
∗
(
a
)为上述问题的解,故有
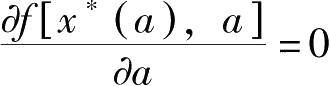 。于是,
。于是,
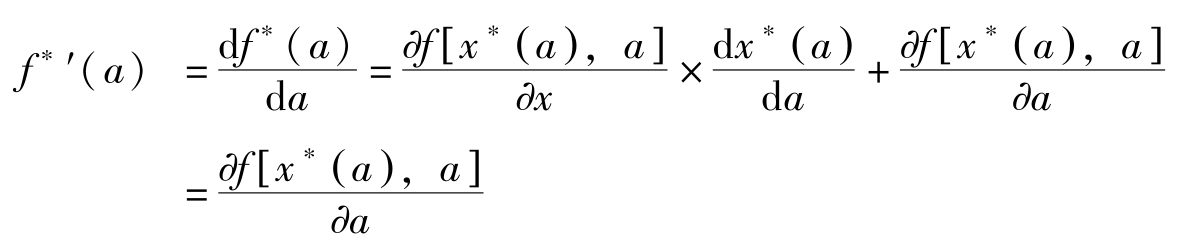
上述包络定理在经济学中有广泛的应用。如在微观经济学中,考虑短期与长期成本曲线的区别。企业投入资本与劳动进行生产,短期内资本投入视为固定,劳动投入可变。用
a
表示短期的生产水平,
z
表示劳动投入,
x
表示资本投入,生产函数为
a
=
F
(
z
,
x
)。成本
f
=
wz
+
rx
,其中
w
,
r
分别表示工资与租金。短期成本是产量的函数,记作
c
s
(
a
),
c
s
(
a
)=
f
(
x
,
a
),其中
x
外生给定。长期中,
x
为可变,对任意给定的产量
a
,企业会选择最优的资本投入使成本最小,长期成本函数
c
l
(
a
)=
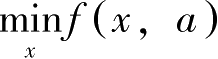 。由包络定理,
c′
l
(
a
)=
c′
s
[
x
∗
(
a
),
a
],也就是说,长期成本曲线在每一产量
a
处都与对应该产量的最优短期生产规模的成本曲线相切,即长期成本曲线为短期成本曲线的包络线。如图1所示。
。由包络定理,
c′
l
(
a
)=
c′
s
[
x
∗
(
a
),
a
],也就是说,长期成本曲线在每一产量
a
处都与对应该产量的最优短期生产规模的成本曲线相切,即长期成本曲线为短期成本曲线的包络线。如图1所示。
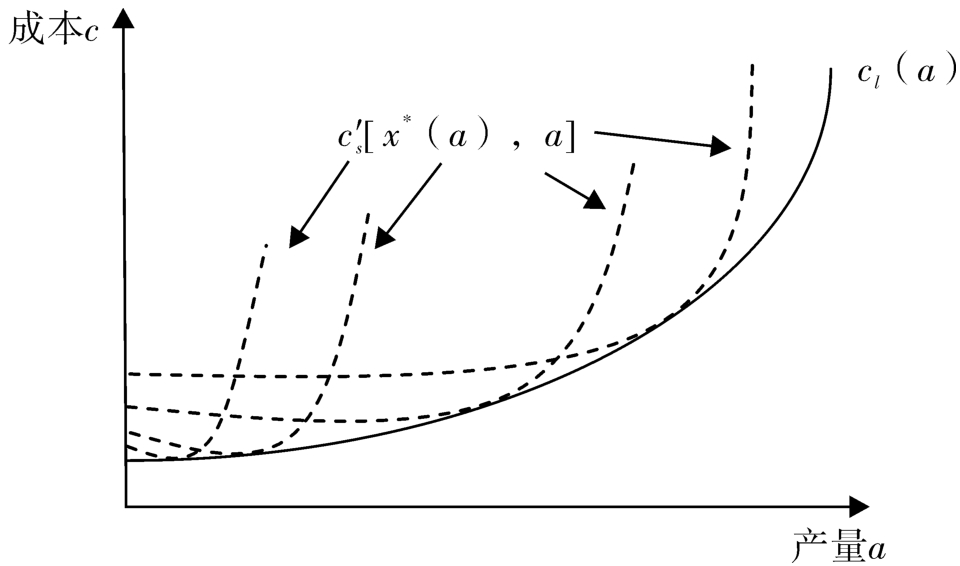
图1 长期成本与短期成本
高级宏观经济学中也经常使用包络定理。如在高级宏观经济学中经常要对Bellman方程进行分析,每次分析我们都会用到包络定理。
定理4(凹性定理):
假定
f
(
x
,
a
):
R
n
×
R
m
→
R
关于(
x
,
a
)凹,且对所有的
a
∈
R
m
,
f
∗
(
a
)=
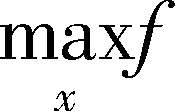 (
x
,
a
)均存在,则
f
∗
:
R
m
→
R
关于
a
凹。
(
x
,
a
)均存在,则
f
∗
:
R
m
→
R
关于
a
凹。
证明: ∀ a , a′ ∈ R m ,记使 f ( x , a )与 f ( x , a′ )分别达到最大的 x 值为 x ∗ ( a ), x ∗ ( a′ )。∀ λ ,0≤ λ ≤1,显然有:
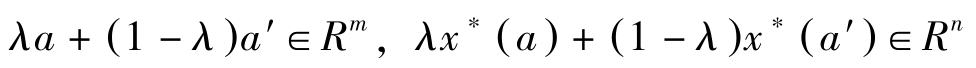
于是
f ∗ [ λa +(1 -λ ) a′ ]=m x ax f [ x , λa +(1 -λ ) a′ ]
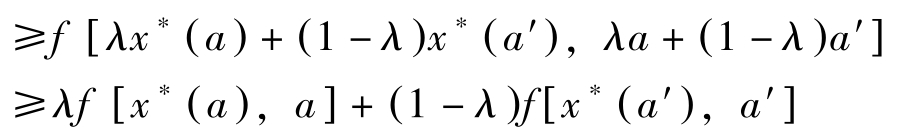
[这是因为 f ( x , a ): R n × R m → R 关于( x , a )凹]
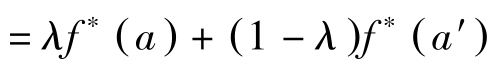
即 f ∗ : R m → R 关于 a 凹。
本节讨论第1章1.1节中的第二种情况,即约束取等号的情况。
先考虑如下两变量问题:
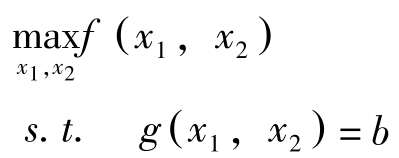
其中 b ∈ R , g 为实函数。
对上述问题构造拉格朗日函数:
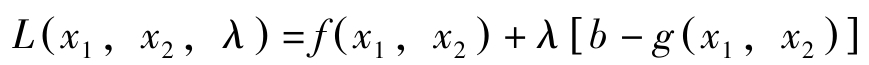
一阶条件为:
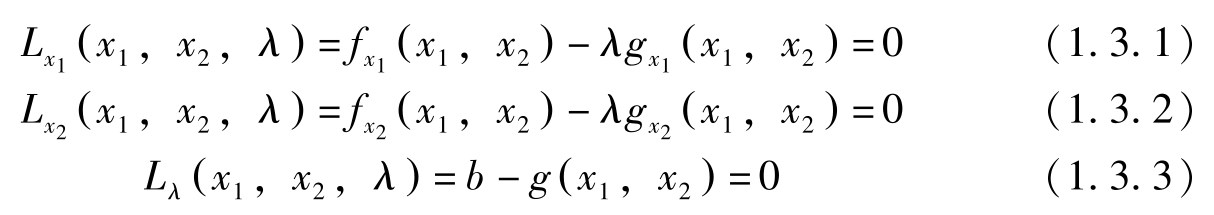
利用上面这三个条件可求最优解
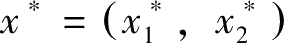 与拉格朗日乘数
λ
∗
。由(1.3.1)有:
与拉格朗日乘数
λ
∗
。由(1.3.1)有:
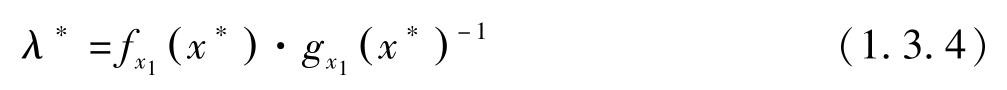
下面看一下拉格朗日乘数的意义。
对约束条件全微分有:
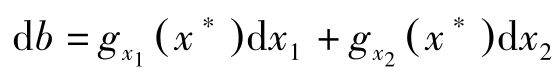
因此,
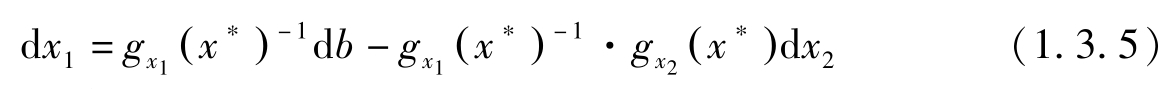
利用(1.3.5)式,有:
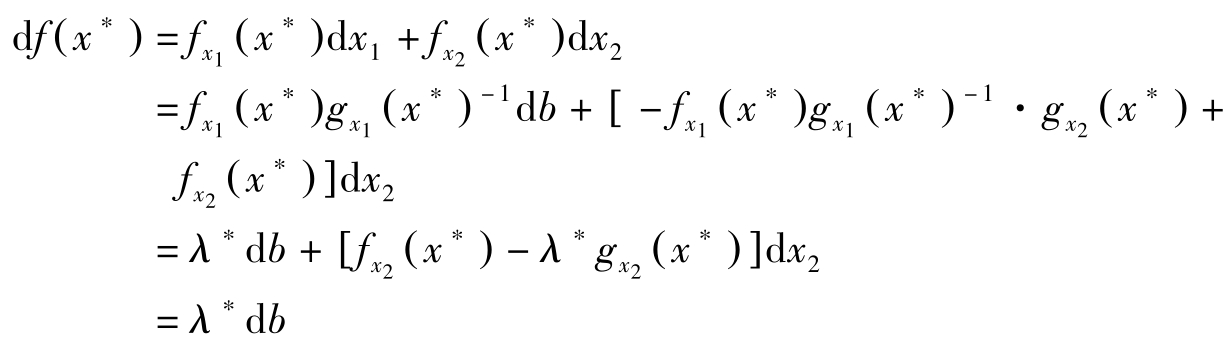
因此, λ ∗ 是资源 b 的最后一单位增加所引起的目标函数最优值的变化,它反映了目标函数对资源 b 的敏感程度。
考虑1.1节中约束取等号的问题:
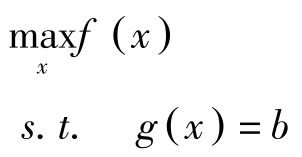
对于上述问题,有如下定理:
定理 5(拉格朗日乘子法): 假定:① f , g 连续可微;② m < n ;③ g′ ( x ∗ )满行秩。记 L ( x , λ )= f ( x )+ λ [ b-g ( x )],若 x ∗ 为上述问题的解,则存在向量 λ ∗ (称为拉格朗日乘数)满足:

证明: 由于 g 满足条件①、②和③,根据隐函数定理,在 x ∗ 近旁可将 x =( x 1 , x 2 ,…, x n )分为两部分: m 维向量 x 1 与 n-m 维向量 x 2 ,使得 x 2 可表示成 x 1 的某一函数 x 2 = h ( x 1 )。于是上述问题可改写成下述无约束的局部最大化问题:
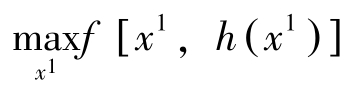
因 f , h 都连续可微,所以该最大化问题的必要条件为:
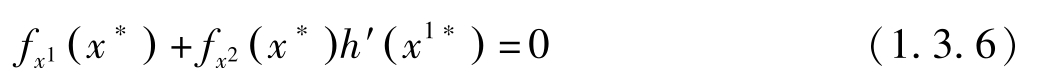
另一方面,预算约束对 x 1 的导数 g x 1 ( x ∗ )+ g x 2 ( x ∗ ) h′ ( x 1∗ )=0,即
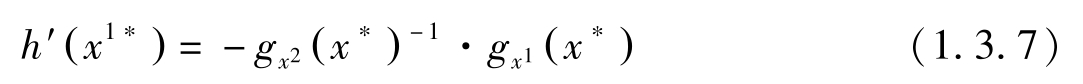
把上式代入(1.3.6)式有:
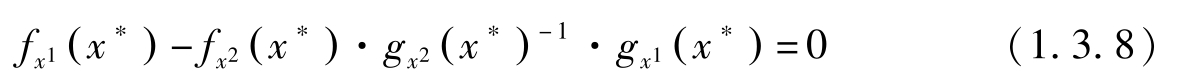
另外,显然有:
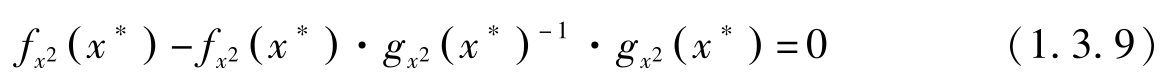
令
λ
∗
=
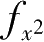 (
x
∗
)·
g
x
2
(
x
∗
)
-1
,并记为
L
(
x
,
λ
)=
f
(
x
)+
λ
[
b-g
(
x
)],则可将(1.3.8)与(1.3.9)式合写为:
(
x
∗
)·
g
x
2
(
x
∗
)
-1
,并记为
L
(
x
,
λ
)=
f
(
x
)+
λ
[
b-g
(
x
)],则可将(1.3.8)与(1.3.9)式合写为:
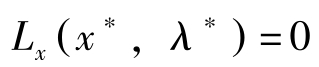
L λ ( x ∗ , λ ∗ )=0显然成立。
下面看一下存在等式约束时的包络定理。
定义
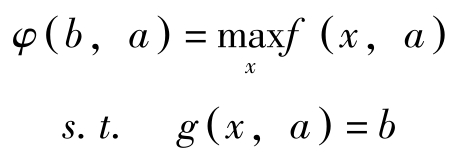
于是
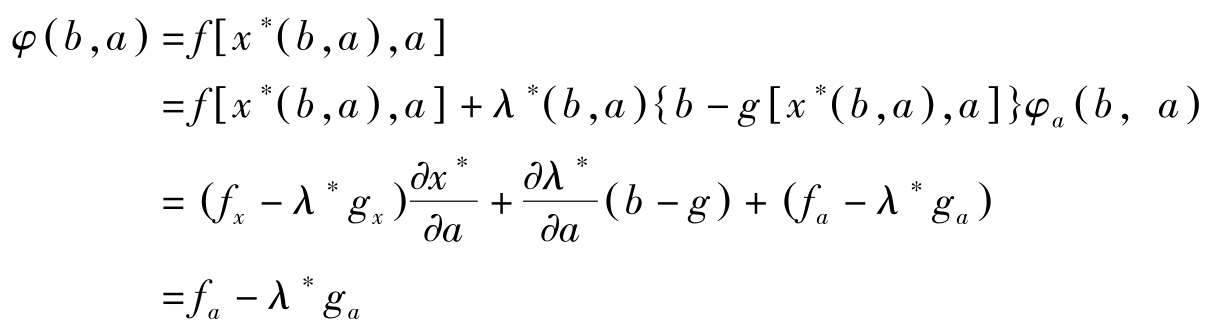
这里用到了一阶条件 f x -λ ∗ g x =0与约束条件 g = b 。
本节讨论1.1节中问题的第三种情况:
(NLP)
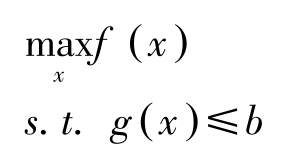
其中, f , g 均为向量 x 的连续实函数。
先考虑两变量的情况。
(NLP)
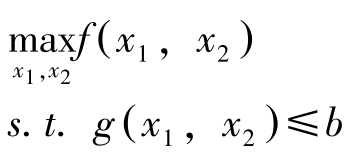
引入松弛变量 s ,将问题变为:
(NLP)
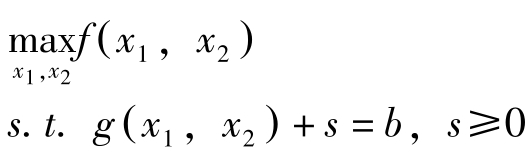
现在,假定最大解为 x ∗ 与 s ∗ 。在 x ∗ 与 s ∗ 处对约束条件全微分有:
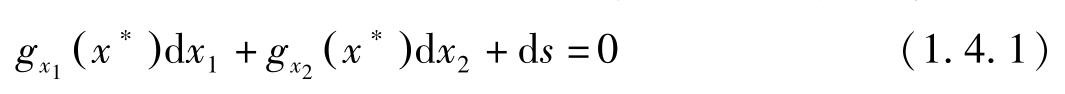
若 g x 1 ( x ∗ )≠0,则由上式可得:
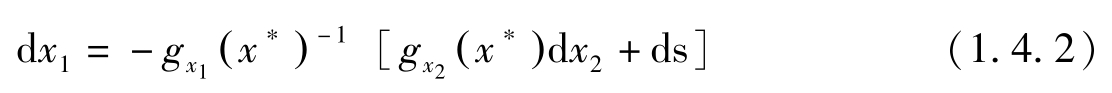
因此若忽略二阶小量,近似有:
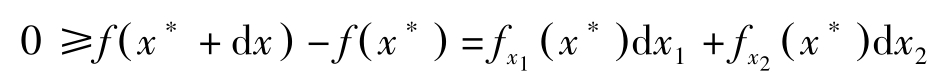
=[ -f x 1 ( x ∗ ) g x 1 ( x ∗ ) -1 g x 2 ( x ∗ )+ f x 2 ( x ∗ )]d x 2 -[ f x 1 ( x ∗ ) g x 1 ( x ∗ ) -1 ]d s 若d s =0,由于d x 2 可正可负,故必有
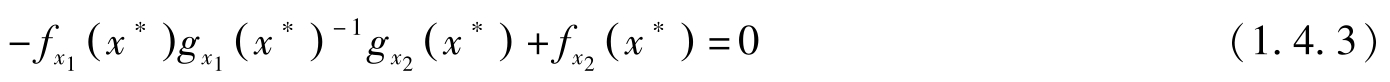
假定d s ≠0,d x 2 =0。注意到 s ≥0,故若 s ∗ =0,则必有d s >0;若 s ∗ >0,则d s 可正可负。因此,当 s ∗ >0 时,必有 f x 1 ( x ∗ ) g x 1 ( x ∗ ) -1 =0;而 s ∗ =0时,必有 f x 1 ( x ∗ ) g x 1 ( x ∗ ) -1 ≥0。
记 f x 1 ( x ∗ ) g x 1 ( x ∗ ) -1 = λ ∗ ,则上述分析表明: λ ∗ ≥0且 λ ∗ s ∗ =0。
另一方面, -f x 1 ( x ∗ ) g x 1 ( x ∗ ) -1 g x 1 ( x ∗ )+ f x 1 ( x ∗ )=0,利用(1.4.3)式我们有:
f x ( x ∗ ) -λ ∗ g x ( x ∗ )=0
记 L ( x , λ )= f ( x )+ λ [ b-g ( x )],则上述问题最优解的必要条件为:
(a) L x ( x ∗ , λ ∗ )= f x ( x ∗ ) -λ ∗ g x ( x ∗ )=0
(b) L λ = b-g ( x ∗ )[= s ∗ ]≥0
(c) λ ∗ L λ = λ ∗ [ b-g ( x ∗ )][= λ ∗ s ∗ ]=0
(d) λ ∗ ≥0
这些必要条件也称为 库恩塔克条件 。需要注意的是:首先,拉格朗日乘数总是非负的(d);其次,拉格朗日乘数为正时松弛变量为0,对应的约束取等号(c);最后,(b)、(c)与(d)意味着 λ ∗ 是 L ( x ∗ , λ )的最小值点。
最后一点可以这样说明:假定 λ ∗ 是 L ( x ∗ , λ )的最小值点,则下式近似成立:
0≤ L ( x ∗ , λ ∗ +Δ λ ) -L ( x ∗ , λ ∗ )= L λ ( x ∗ , λ ∗ )Δ λ
若 λ ∗ >0,则Δ λ 可正可负;要使上式成立,必有 L λ =0;
若 λ ∗ =0,则Δ λ 只能大于等于0;要使上式成立,必有 L λ ≥0。
记
I
(
x
)={
i|g
i
(
x
)=
b
i
},若等式约束的导函数向量的集合,而
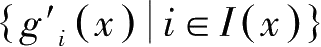 在
x
处的元素线性独立,则称
g
在
x
处满足正则条件。
在
x
处的元素线性独立,则称
g
在
x
处满足正则条件。
若对所有的 i , g i 均为连续可微的凸函数,且存在 x 0 ∈ R n 使 g i ( x 0 )< b i ,则称 g 满足凸性与Slater条件。
若约束满足正则条件或满足凸性与Slater条件,则(NLP)的最大解 x ∗ 满足库恩塔克条件(定理8与定理9会加以证明)。即存在 λ ∗ 使(a)、(b)、(c)和(d)成立。此时若 f 为凹函数, g i 均为凸函数,则 L ( x , λ )关于 x 凹,关于 λ 线性。于是(a)式意味着对所有的 x ∈ R n ,有
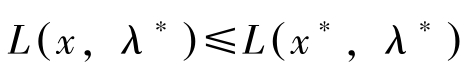
这是因为 L ( x , λ ∗ ) -L ( x ∗ , λ ∗ )≤ L x ( x ∗ , λ ∗ )( x-x ∗ )=0。
另一方面,(b)、(c)与(d)意味着对任意的 λ ≥0, λ 转置 ∈ R m ,有
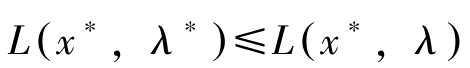
我们称( x ∗ , λ ∗ )为鞍点。因此有如下定理:
定理6: 假定 f 为凹函数且约束满足正则性、或满足凸性与Slater 条件。若 x ∗ 是(NLP)的最大解,则存在 λ ∗ ≥0,使( x ∗ , λ ∗ )为鞍点。
定理7(Fritz John): 假定 f , g 连续可微。若 x ∗ 是(NLP)的最优解,则存在 m +1维向量 η =( η 0 , η 1 ,…, η m )>0,使得
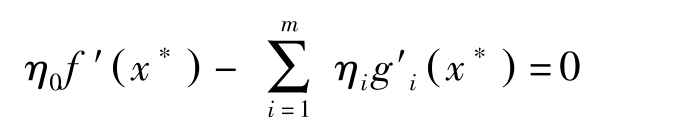
η i [ b i -g i ( x ∗ )]=0
g i ( x ∗ )≤ b i ( i =1,2,…, m )
成立。
证明:
记
z
1
(
x
∗
)={
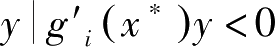 ,
i
∈
I
(
x
∗
);
y
∈
R
n
};
z
2
(
x
∗
)={
y|f′
(
x
∗
)
y
>0;
y
∈
R
n
};这里
I
(
x
∗
)={
i|g
i
(
x
∗
)=
b
i
}。
,
i
∈
I
(
x
∗
);
y
∈
R
n
};
z
2
(
x
∗
)={
y|f′
(
x
∗
)
y
>0;
y
∈
R
n
};这里
I
(
x
∗
)={
i|g
i
(
x
∗
)=
b
i
}。
首先证明:若 x ∗ 为最大解,则 z 1 ( x ∗ )∩ z 2 ( x ∗ )= φ 。
由于这两个集合均为开集,故对于 y ∈ z 1 ( x ∗ )∩ z 2 ( x ∗ ),取充分小的正数 ε >0,按微分中值定理,存在0< θ <1与0< θ′ <1使得
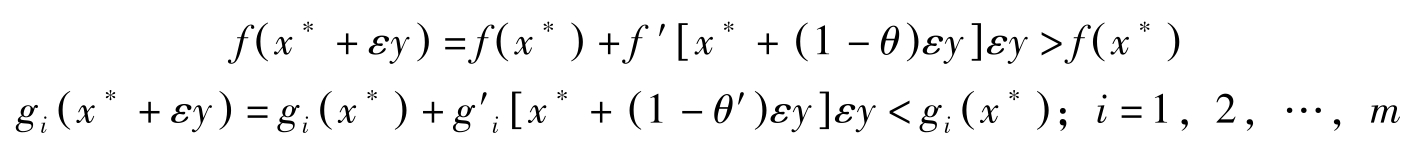
因此 g i ( x ∗ + εy )≤ b i ; i =1,2,…, m 且 f ( x ∗ + εy )> f ( x ∗ )。这与 x ∗ 是最大解矛盾!
这说明若 x ∗ 为最大解,则 z 1 ( x ∗ )∩ z 2 ( x ∗ )= φ ,这两个集合是分离的。
若 I ( x ∗ )={ i 1 , i 2 ,…, i k },则有:
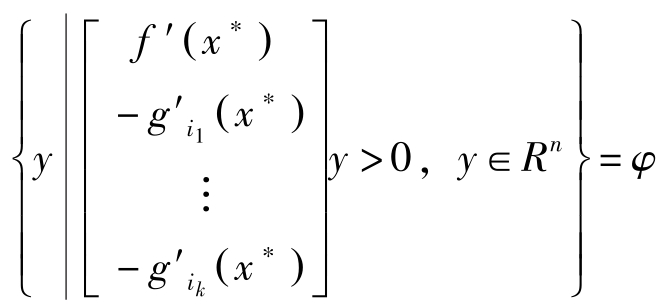
其次,利用上式与Gordan定理,存在( η 0 , η i 1 ,…, η i k )>0满足:
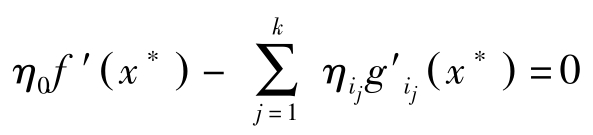
再加上对 i ∉ I ( x ∗ ),即 g i ( x ∗ )< b i ,让 η i =0。于是
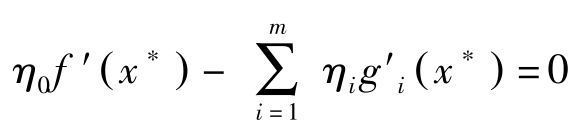
证毕。
所谓Gordan定理是指:对于 m 个 n 维行向量 a i =( a i 1 , a i 2 ,…, a in ), i =1,2,…, m ,要么存在 n 维列向量 y 使得
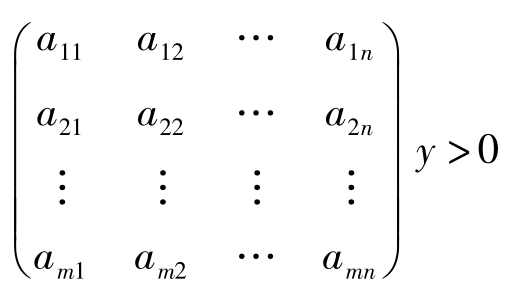
要么存在 m 维列向量 η >0使得
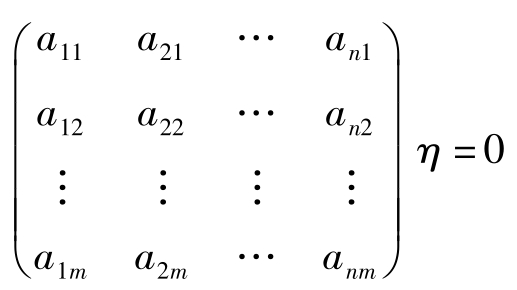
二者不可得兼。
定理8: 假定 f , g 连续可微,且 g 在 x ∗ 处满足正则性。若 x ∗ 是(NLP)的最大解,则库恩塔克条件(a)、(b)、(c)与(d)必成立。
证明:
令
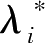 =
η
i
/η
0
,只需证明
η
0
≠0即可。
=
η
i
/η
0
,只需证明
η
0
≠0即可。
假定
η
0
=0,则
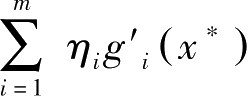 =0。由于
η
>0(不全为0),故
g
的导函数向量线性相关,与正则性矛盾!
=0。由于
η
>0(不全为0),故
g
的导函数向量线性相关,与正则性矛盾!
定理9: 假定 f , g 连续可微,且 g 满足凸性及 Slater 条件。 x ∗ 若是(NLP)的最大解,则必满足库恩塔克条件。
证明:
只需证明
η
0
≠0 即可。因
g
满足 Slater 条件,故存在
x
0
∈
R
n
使
g
(
x
0
)<
b
。又因
g
满足凸性,故对所有的
i
,
g
i
(
x
0
)
-g
i
(
x
∗
)≥
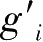 (
x
∗
)(
x
0
-x
∗
)。
(
x
∗
)(
x
0
-x
∗
)。
因 η =( η 0 , η 1 ,…, η m )非负,故
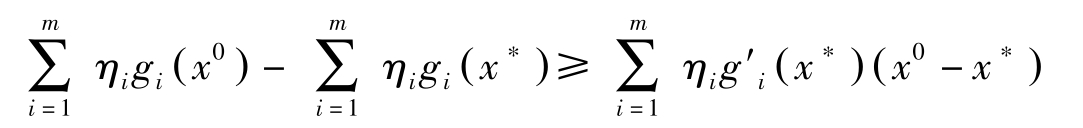
这里,若
η
0
=0,则由定理7第一式知
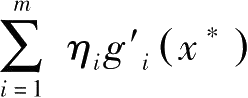 =0,于是
=0,于是
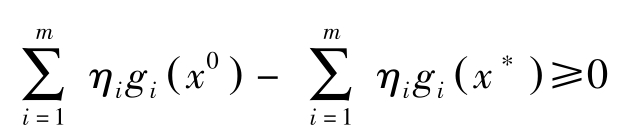
因而,
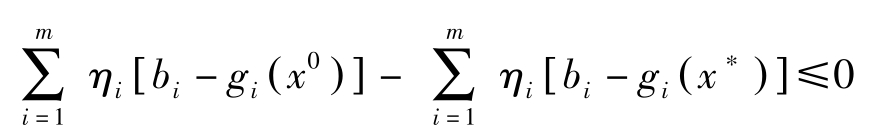
由定理7第二式知
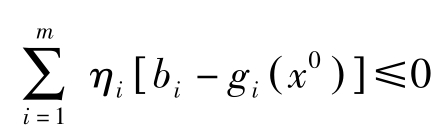
因 η =( η 0 , η 1 ,…, η m )>0, η 0 =0,故( η 1 ,…, η m )>0。由Slater条件知对所有的 i ,都有 g i ( x 0 )< b i ,于是有
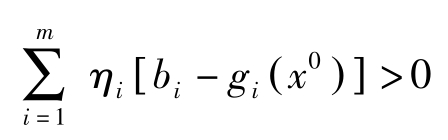
矛盾!
定理10(库恩塔克条件的充分性): 假定 f , g 连续可微, f 为凹函数,且 g i 对所有的 i 均为凸函数。若 x ∗ 满足库恩塔克条件,则其必为(NLP)的最大解。
证明: 定义集合 I , J 如下
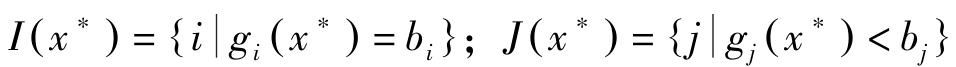
对任意满足 b ≥ g ( x )的 x 以及所有的 i ∈ I ( x ∗ ),有 b i = g i ( x ∗ )≥ g i ( x )。由于 g i 是凸函数,故对所有的 i ∈ I ( x ∗ ),均有 g′ i ( x ∗ )( x-x ∗ )≤0。
由于
λ
∗
≥0,故对所有的
i
∈
I
(
x
∗
),
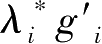 (
x
∗
)(
x-x
∗
)≤0。
(
x
∗
)(
x-x
∗
)≤0。
由库恩塔克条件(b)、(c)与(d)可知,对所有的
j
∈
J
(
x
∗
),
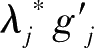 (
x
∗
)(
x-x
∗
)=0。故
λ
∗
g′
(
x
∗
)(
x-x
∗
)≤0。
(
x
∗
)(
x-x
∗
)=0。故
λ
∗
g′
(
x
∗
)(
x-x
∗
)≤0。
另一方面, f 的凹性及条件(a)意味着
f ( x ) -f ( x ∗ )≤ f′ ( x ∗ )( x-x ∗ )= λ ∗ g′ ( x ∗ )( x-x ∗ )≤0
这就是说, f ( x ∗ )是最大值。
推论1: 假定 f , g 连续可微, f 凹, g 凸且满足 Slater 条件,则 x ∗ 是(NLP)最大解的充要条件是它满足库恩塔克条件。
考虑下述问题:
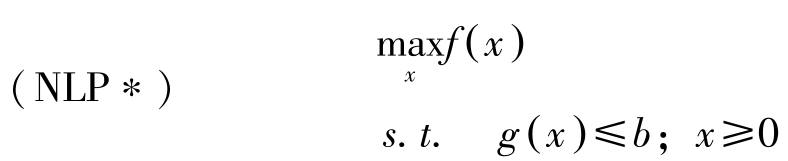
构造拉格朗日函数,
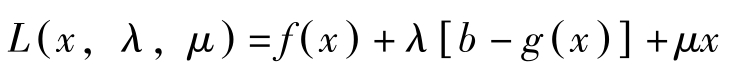
库恩塔克条件为:
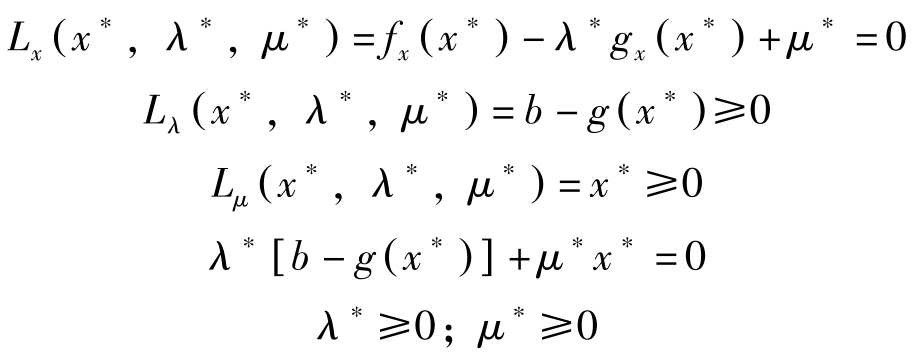
消去 μ ∗ ,可将这些条件归结为对 L ( x , λ )= f ( x )+ λ [ b-g ( x )]:
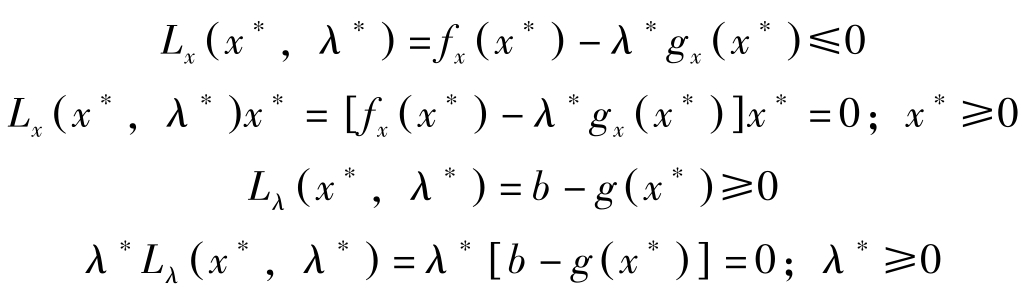
以上是存在非负约束时的库恩塔克条件。
定理11: 假定 f 凹, g 凸。 x ∗ 若是(NLP)的最优解,则存在 m +1维向量 η =( η 0 , η 1 ,…, η m )>0,使得对任意的 x ∈ R n ,有
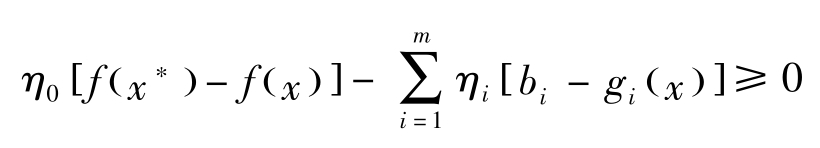
定理7假定 f 与 g 连续可微,而定理11假定 f 凹, g 凸。该定理的证明须利用一般化的Gordan定理(Fan,Glicksberg,Hoffman定理):
对定义在
R
n
上的凸函数
h
0
,
h
1
,…,
h
m
,或者①存在
y
0
∈
R
n
,使对所有的
i
都有
h
i
(
y
0
)<0,或者②对所有的
y
∈
R
n
都存在
η
=(
η
0
,
η
1
,…,
η
m
)>0使得
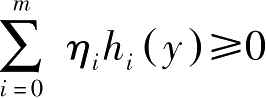 。但二者不可兼得。
。但二者不可兼得。
上述一般化定理中若令 h i ( y )= a i y ,即可得到前面的Gordan定理。
现在证明定理11。令
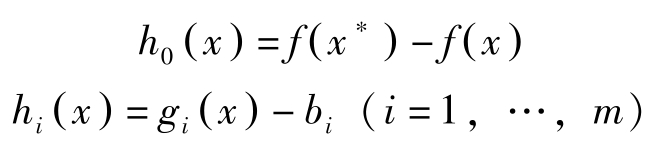
因 f 凹, g 凸,故 h 0 ( x )与 h i ( x ), i =1,…, m 皆为凸函数。由于 x ∗ 是(NLP)的最优解,故使
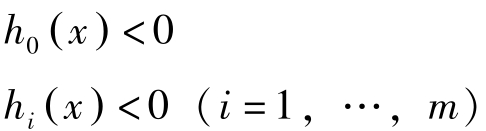
成立的 x ∈ R n 不存在。根据一般化的Gordan定理,存在 η =( η 0 , η 1 ,…, η m )>0,使得对任意的 x ∈ R n ,有
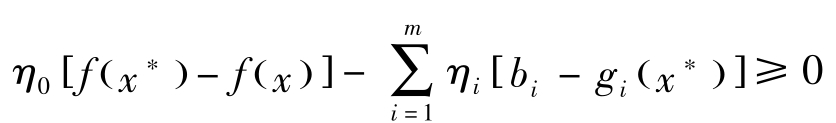
成立。
定理12: 假定 f 凹, g 凸且满足Slater条件。 x ∗ 若是(NLP)的最优解,则必存在 λ ∗ ≥0,使( x ∗ , λ ∗ )满足鞍点条件。
证明: 假定 η 0 =0,于是对任意的 x ∈ R n ,均有
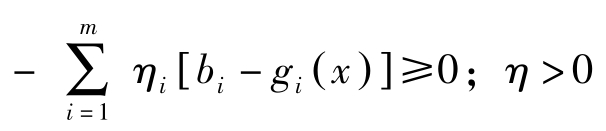
因 η =( η 0 , η 1 ,…, η m )>0, η 0 =0,故( η 1 ,…, η m )>0。由Slater条件知存在 x 0 ∈ X ⊂ R n ,对所有的 i ,都有 g i ( x 0 )< b i ,于是有
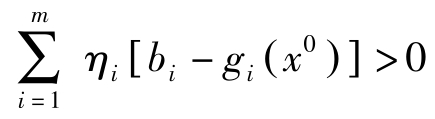
矛盾!因此, η 0 ≠0。
令
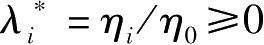 ,则Fritz John不等式变为
,则Fritz John不等式变为
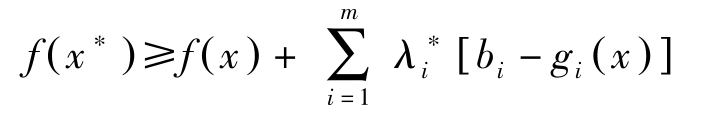
现在令
x
=
x
∗
,则有
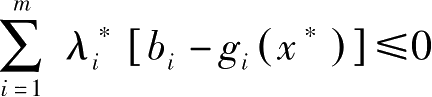 ,但
,但
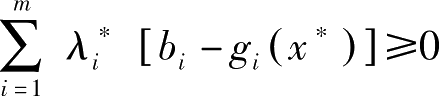 ,因此
,因此
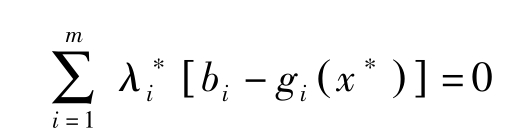
令
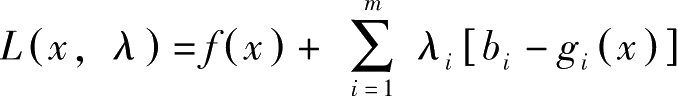 ,则
,则
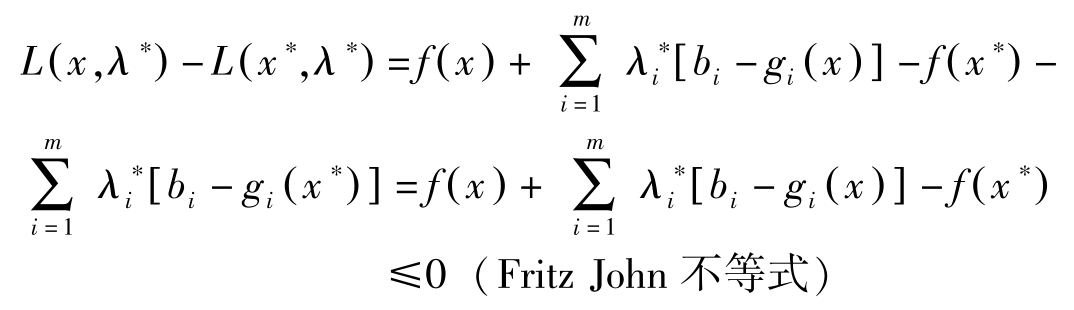
另一方面,
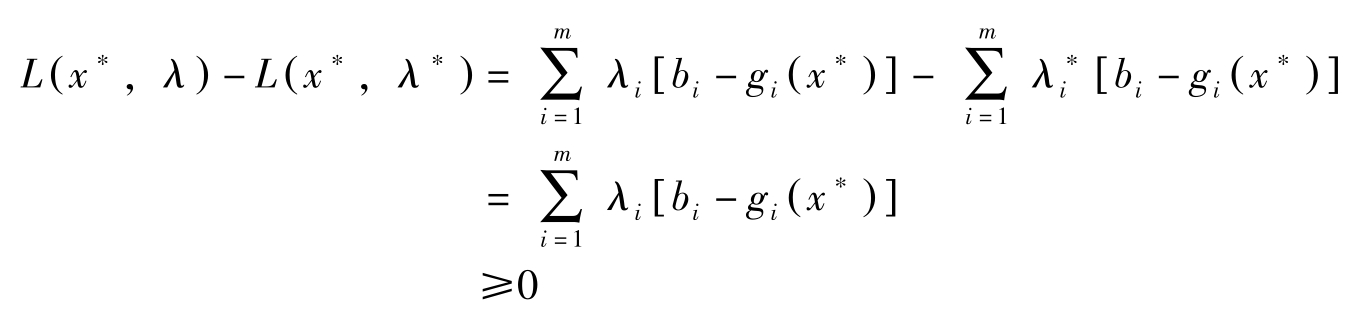
因此( x ∗ , λ ∗ )满足鞍点条件。
定理13: 对于 x ∗ ,若存在 λ ∗ ≥0使得( x ∗ , λ ∗ )满足鞍点条件,则 x ∗ 为(NLP)的最大解。
证明: 因( x ∗ , λ ∗ )为鞍点,对所有的 x ∈ R n 与 λ ≥0, λ 转置 ∈ R m ,
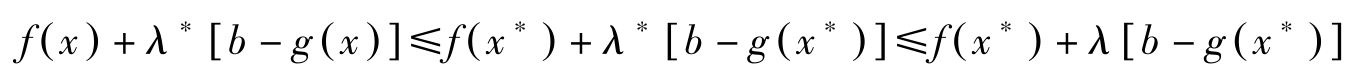
从上式的后一个不等式可得( λ-λ ∗ )[ b-g ( x ∗ )]≥0。该式对 λ =0 也成立,因而
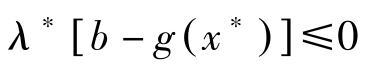
让
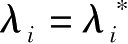 ,
i
=1,…,
j
-1,
j
+1,…,
m
;
λ
j
=
,
i
=1,…,
j
-1,
j
+1,…,
m
;
λ
j
=
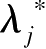 +1,则
b
j
≥
g
j
(
x
∗
),由于
j
是任意的,所以
b
≥
g
(
x
∗
)。于是
λ
∗
[
b-g
(
x
∗
)]≥0。故
+1,则
b
j
≥
g
j
(
x
∗
),由于
j
是任意的,所以
b
≥
g
(
x
∗
)。于是
λ
∗
[
b-g
(
x
∗
)]≥0。故
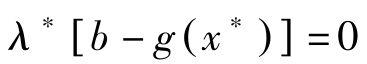
下面考虑满足 b ≥ g ( x )的 x 。因 f ( x )+ λ ∗ [ b-g ( x )]≤ f ( x ∗ )+ λ ∗ [ b-g ( x ∗ )],故
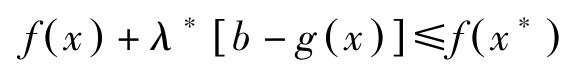
因此, x ∗ 为(NLP)的最大解。
推论2: f 凹, g 凸且满足Slater条件。 x ∗ 若是(NLP)的最大解的充要条件是 x ∗ 满足鞍点条件。
考虑(NLP),假定 x ∗ 满足库恩塔克条件。于是存在 λ ∗ ,使得:
(a) L x ( x ∗ , λ ∗ )= f x ( x ∗ ) -λ ∗ g x ( x ∗ )=0
(b) L λ ( x ∗ , λ ∗ )= b-g ( x ∗ )≥0
(c) λ ∗ L λ = λ ∗ [ b-g ( x ∗ )]=0
(d) λ ∗ ≥0
成立。
记 I ( x ∗ )={ i|g i ( x ∗ )= b i }; J ( x ∗ )={ j|g j ( x ∗ )< b j }。上述条件可改写为
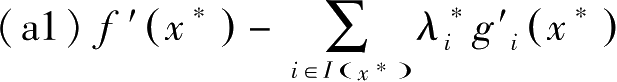 =0
=0
(b1) b i -g i ( x ∗ )=0; i ∈ I ( x ∗ )
(c1
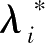 ≥0;
i
∈
I
(
x
∗
)
≥0;
i
∈
I
(
x
∗
)
(d1
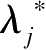 =0;
j
∈
J
(
x
∗
)
=0;
j
∈
J
(
x
∗
)
(a1)成立是因为(d1)成立。
因此 x ∗ 只依赖于 b i ; i ∈ I ( x ∗ ),不依赖于 b j ; j ∈ J ( x ∗ )。所以
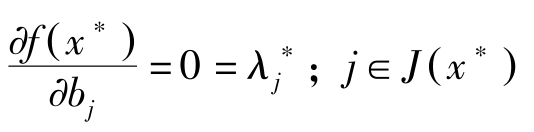
另一方面,(a1)与(b1)所对应的拉格朗日乘数与下述问题对应相同
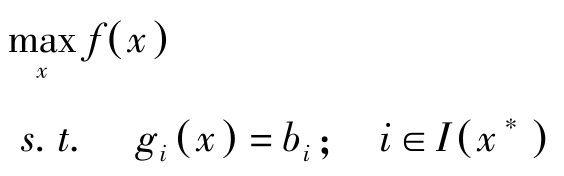
该问题是等式约束最大化问题,
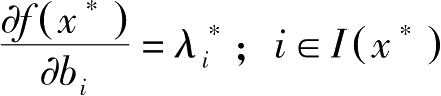 。因此
。因此
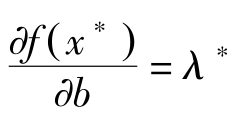
也就是说库恩塔克乘数和拉格朗日乘数具有相同的意义。