




从微观基础出发、采用一般均衡的分析框架研究宏观经济问题有两种基本模型方法:一种是代表性家庭模型,另一种是重叠世代模型。本章介绍代表性家庭模型及其在研究最优增长问题和分析财政政策效果等方面的应用。
这种模型的前提是假定消费者永远存活,不考虑人口增长与技术进步。
(1)效用函数。
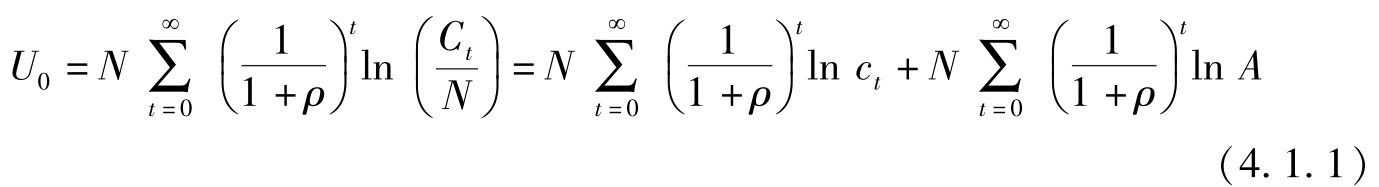
其中 N , C t , A 与 ρ 分别表示总人口、 t 期总消费、技术水平与贴现率, c t = C t / ( AN )。上式中最后一项是常数,求最优解时可不予考虑。
(2)预算约束。
在 t 期,家庭预算约束为:
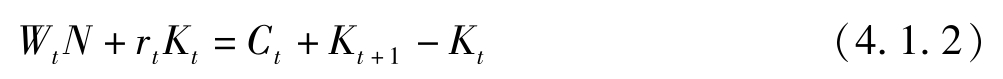
两边同除以 AN ,约束变为:

其中 w t = W t /A , k t = K t / ( AN )。
(3)最优解的必要条件。
家庭在预算约束(4.1.3)下最大化效用(4.1.1),即家庭求解:
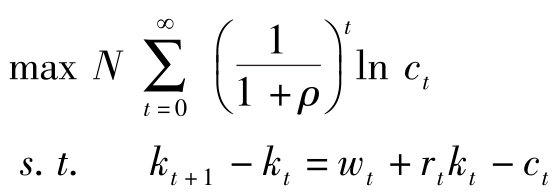
构造现值的Hamilton函数:
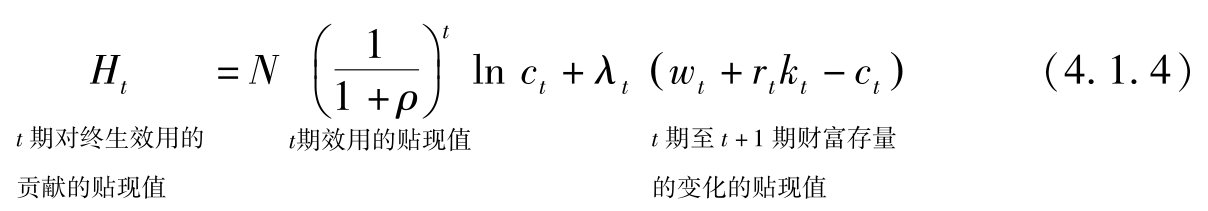
上式左边代表 t 期对终生效用的贡献的贴现值,它是 t 期效用贴现值和 t 期至 t +1期财富存量的变化的贴现值的加总,二者均被贴现到 t =0。
λ t 是共状态变量,它测度 t 期末资本(财富)增加一个单位所带来的终生效用的最大可能的增加值(现值)。因此,它是 t 期的单位资本的边际价值(用现值衡量)或影子价格(用现值衡量)。
右边最后一项是财富价值的变化,表示 t 期到 t +1期由于财富 w t + r t k t -c t 的变动引起资本存量的变动即净投资的影子价值 λ t ( k t +1 -k t )的现值。
一阶条件:
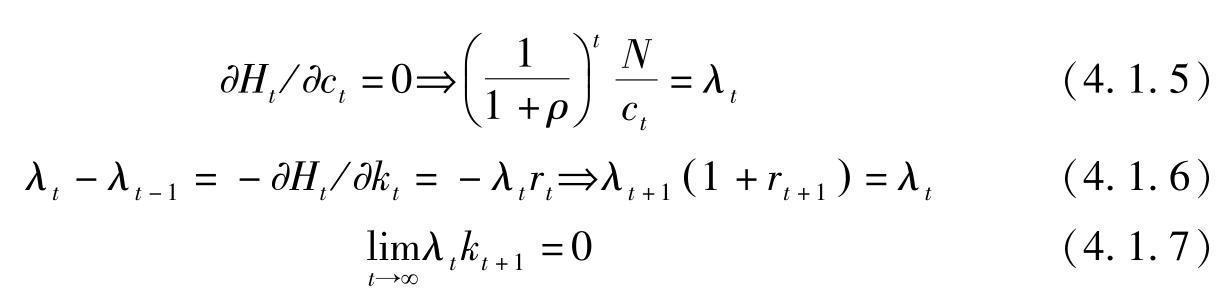
由(4.1.5)与(4.1.6)可得消费的Euler方程式:

资本折旧率假定为 δ 。
生产函数为:
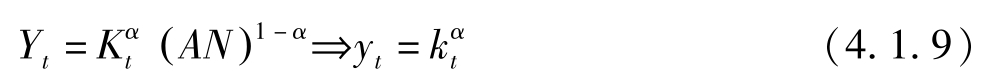
其中 y t = Y t / ( AN ); k t = K t / ( AN )。
利润函数为:
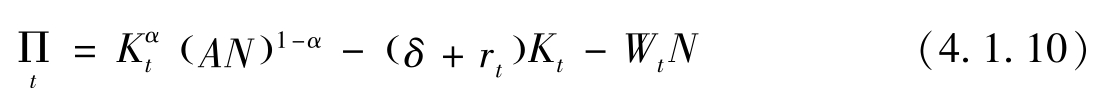
利润最大化要求:

把(4.1.11)与(4.1.12)代入约束条件有:
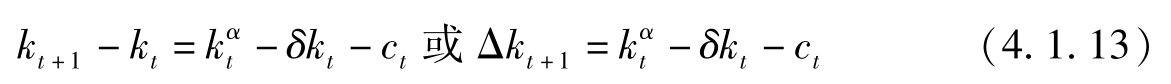
(4.1.13)是关于供给方的第一个均衡条件,是技术条件。
消费的Euler方程(4.1.8)可以改写为:
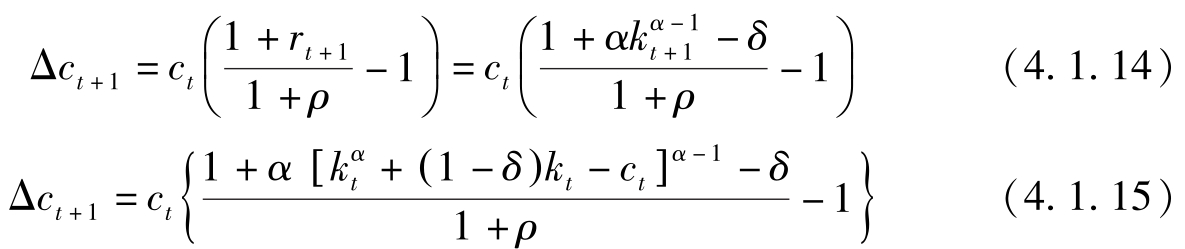
该式可称为偏好条件。
在稳态,
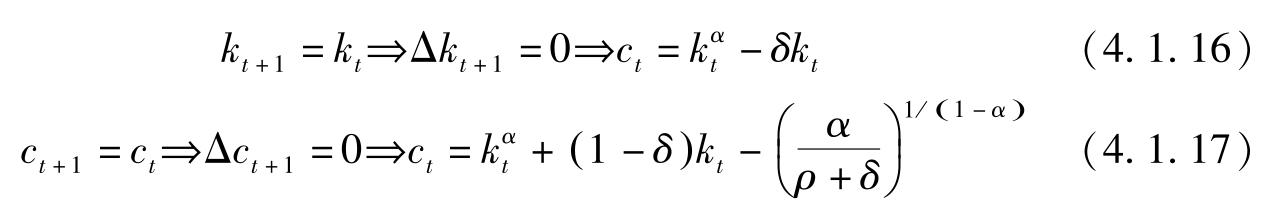
其中(4.1.17)式的推导用到了(4.1.15)式。
下面看一下动力学。
由(4.1.13)式知:

或者说:
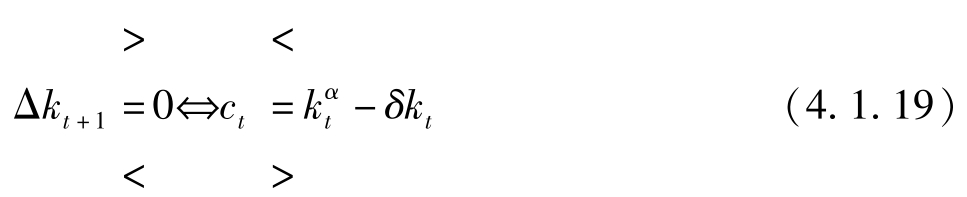
再由(4.1.15)式知:

或者说:
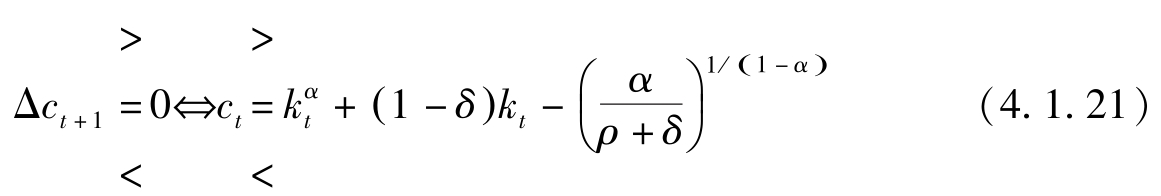
因此,存在鞍点路径,稳态是稳定的。
由(4.1.16)式知,使稳态消费最大的黄金资本存量 k GR 满足:

而利润最大化要求 f′ ( k t )= δ + r t ,因此稳态的 k < k GR ,不会存在过度投资,均衡是Pareto有效的(若稳态的 k > k GR ,则需减少 k 以增大消费,这不需要任何代价就可办到。每个人的消费、效用都还可以增加,也就是说存在Pareto改进,目前的稳态是无效率的。相反,若稳态的 k < k GR ,则需要增加 k 才能增大消费,不存在Pareto改进的余地,此时的经济是动态有效的)。
从(4.1.16)与(4.1.17)可知,较高的 ρ 会降低稳态的 k 与 c 。较之其他国家,如果一国消费者看轻未来消费( ρ 变大),这个国家会变穷。
对于下述问题:
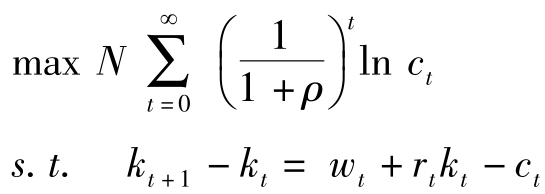
我们还可以尝试采用其他几种不同的方法来求解。
(1)拉格朗日乘子法与现值Hamilton。
建立拉格朗日函数:
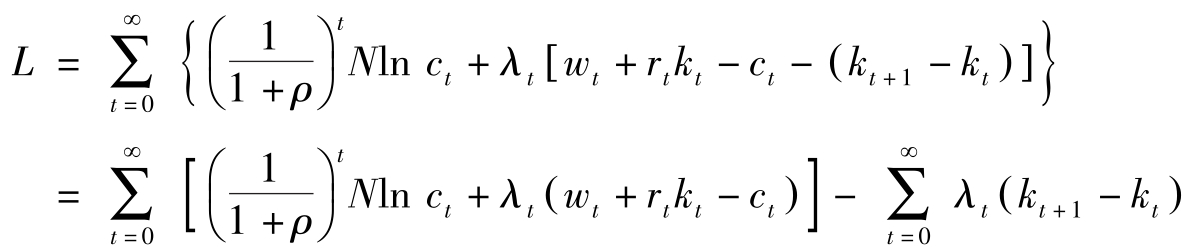
由于
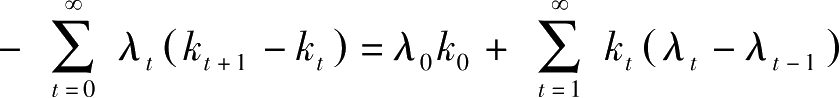 ,因此
,因此
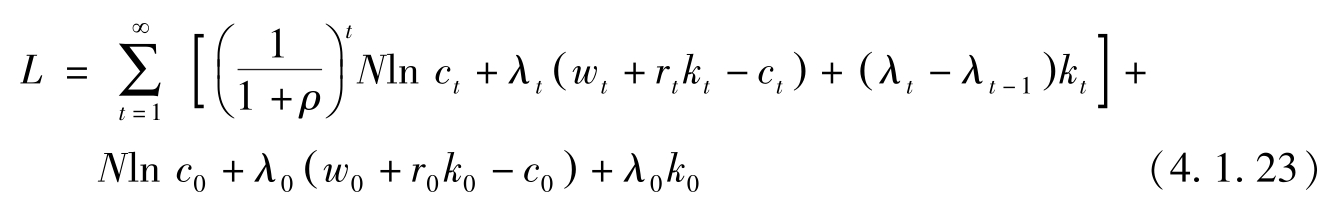
关于 k t 与 c t 的一阶条件为:

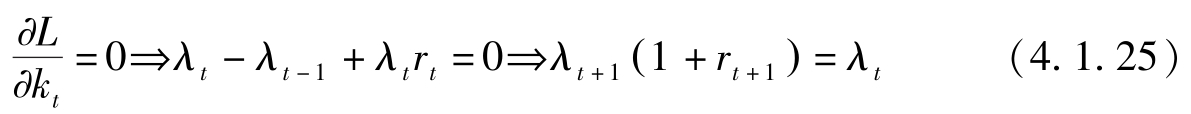
这些条件与(4.1.5)和(4.1.6)相同。
我们可将上述讨论与现值Hamilton联系起来。(4.1.23)中拉格朗日函数可用(4.1.4)中的Hamilton函数改写为:
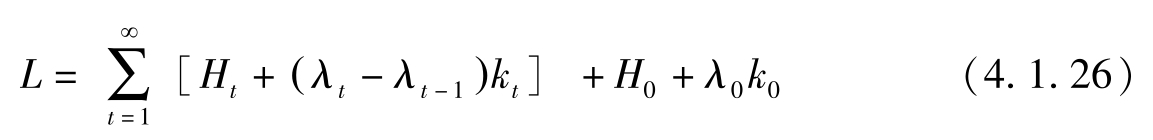
拉格朗日函数两边分别对 c t , k t 求导有:
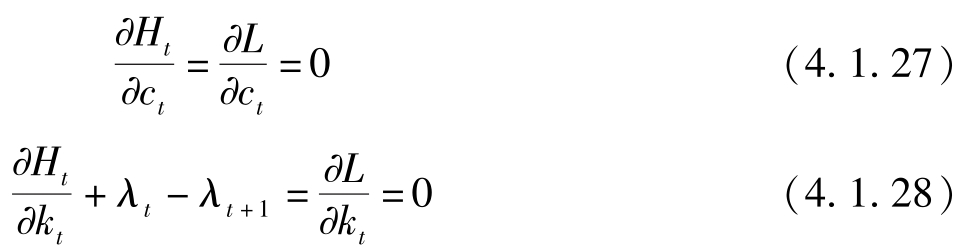
这两个式子分别等价于(4.1.5)与(4.1.6)式。
下面看一下横截性条件。它从哪里来?为解释这一问题,先假定消费者能存活 T +1期( t =0,1,…, T ),则拉格朗日函数变为:
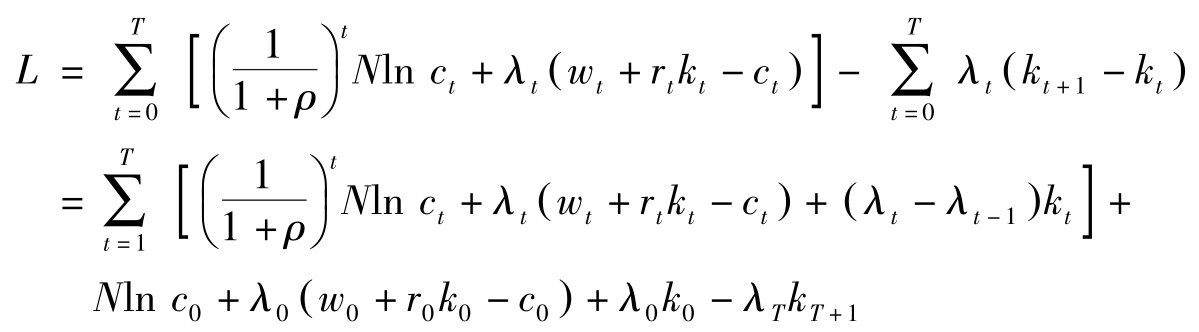
看一下上面这个式子,很明显,要最大化 L ,须让:

但是我们并不清楚是 λ T =0还是 k T +1 =0,或者两者均为0。下面要证明 k T +1 =0(也就是说消费者死后什么都不留,生前全部吃光)。我们再引入约束:
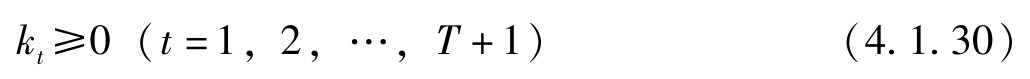
这样的话,上面的拉格朗日函数变为:
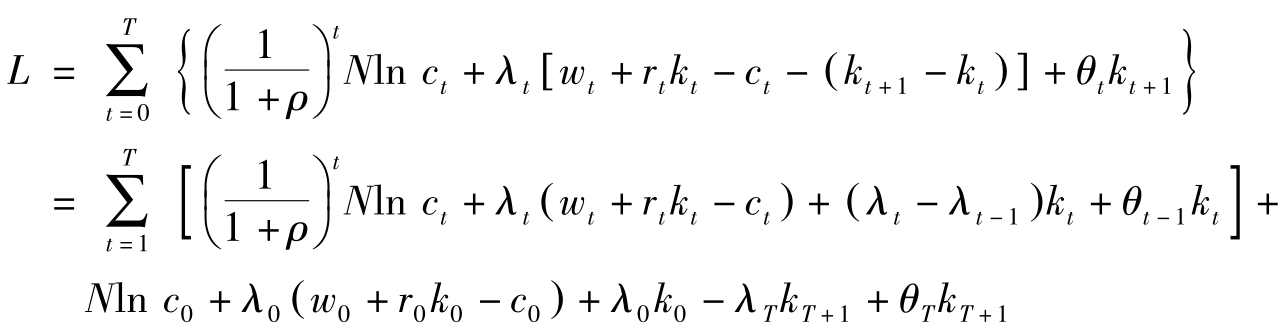
一阶条件是:
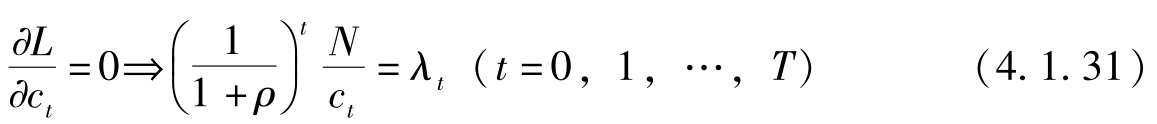
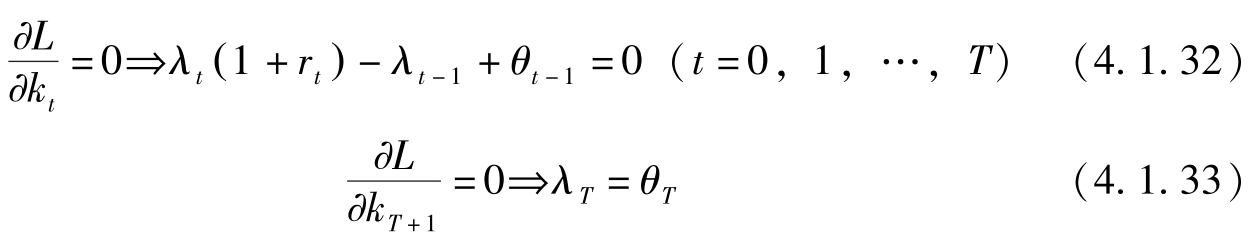
此外,库恩塔克条件是:
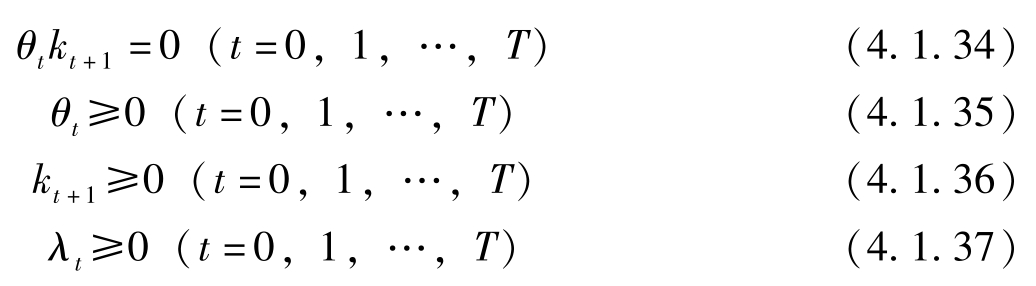
其中(4.1.34)为互补松弛性条件。利用该条件和(4.1.33),当 t = T 时,有

由(4.1.31)式, λ t >0( t =0,1,…, T )。因此 λ T >0,故 k T +1 =0。
因 λ t >0( t =0,1,…, T ),故 k t >0( t =0,1,…, T ),由(4.1.34)得 θ t =0( t =0,1,…, T -1)。这样,由(4.1.31)与(4.1.32)很容易推导出消费的Euler方程(4.1.8)。
当计划期界为无穷时,横截性条件为:

(2)最优控制:当期值的Hamilton函数。
令 μ t =(1+ ρ ) t λ t ,那么 μ t 为财富或资本的影子价格的当期值。记当期值的Hamilton函数为:
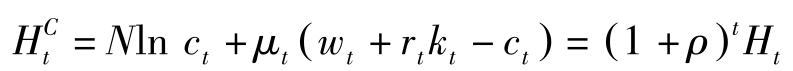
则拉格朗日函数可写为:
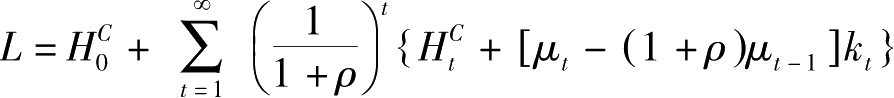 一阶条件:
一阶条件:
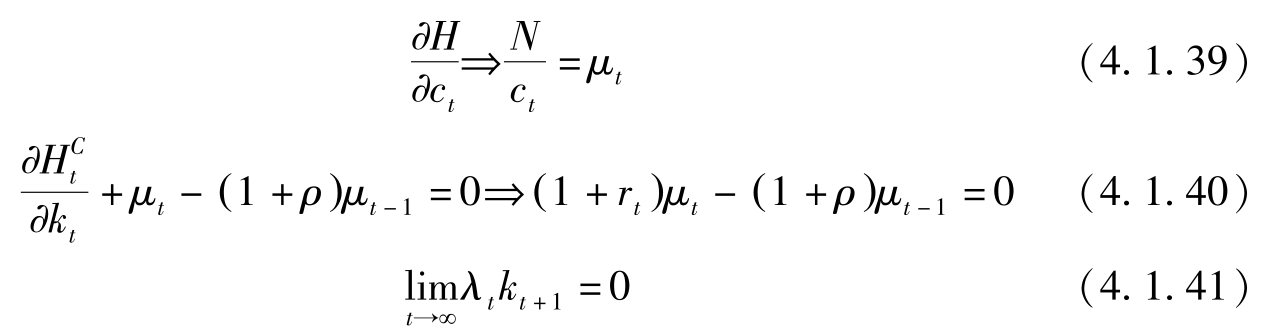
由(4.1.39)与(4.1.40)很容易推出消费的Euler方程(4.1.8)。
(3)直接替代。
将约束条件改为 c t = w t + r t k t -( k t +1 -k t ),并代入目标函数:
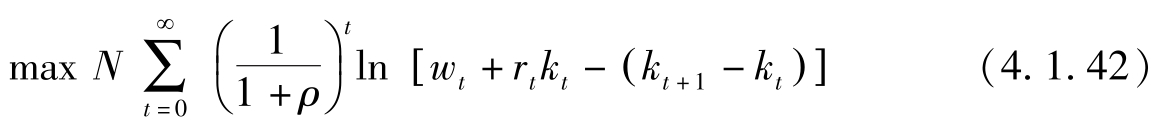
一阶条件(对 k t 求导):
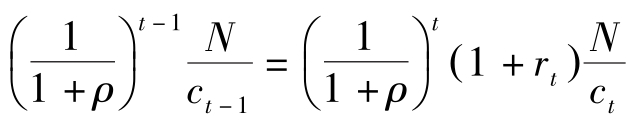
上式左边表示 t -1期的消费减少1单位导致的效用减少的现值, t -1期减少的1单位, t 期变成了1+ r t 单位,用于消费,导致效用增加,右边即为增加的效用的现值,在最优的路径上二者应相等。整理该方程即可得到消费的Euler方程。
(4)动态规划。
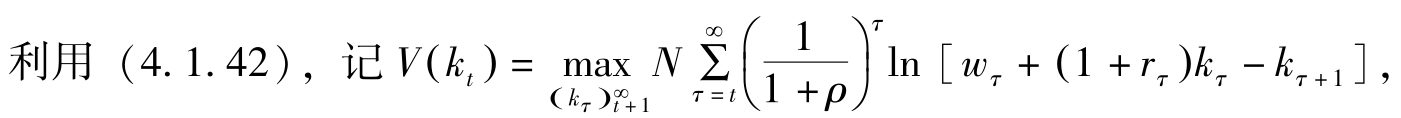
则有Bellman 方程:
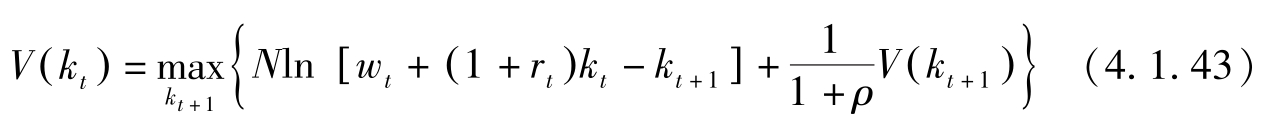
假定价值函数连续可微。(4.1.43)关于 k t +1 的一阶条件是:

(4.1.43)的两边对 k t 求导有(包络定理):

由以上两式很容易推出消费的Euler方程。
(5)另一种拉格朗日方法。
预算约束为 k t +1 = w t +(1+ r t ) k t -c t ,即
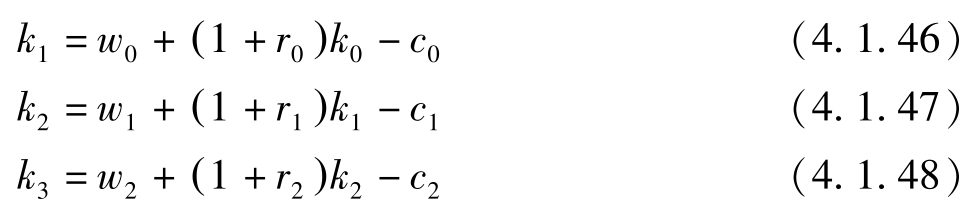
将(4.1.46)代入(4.1.47)有:
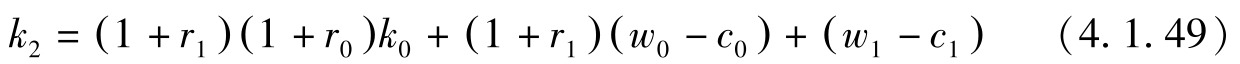
将(4.1.49)代入(4.1.48)有:
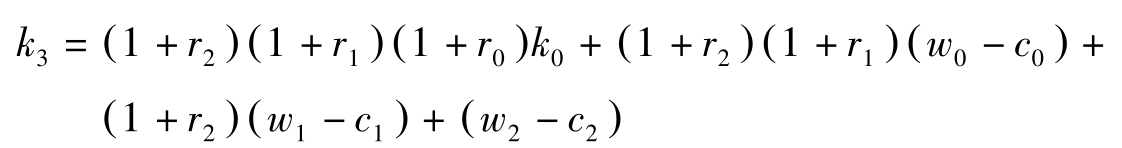
记 R t ≡(1 +r t )…(1 +r 1 )(1 +r 0 ),则上式可写为:
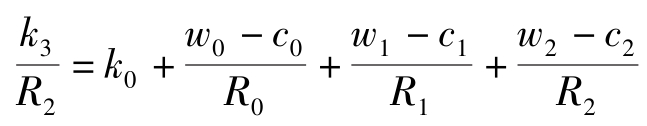
一般有:
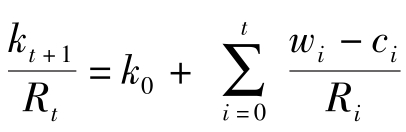
当 t →∞时,左边极限为0,即初始资产与终生收入的现值必须等于消费的现值。
构造拉格朗日函数:
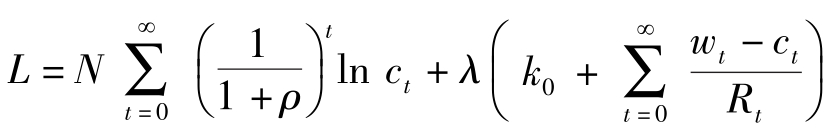
一阶条件:
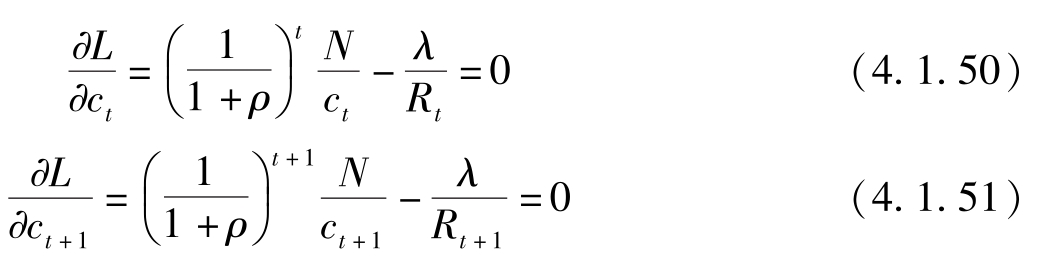
以上两式移项后相除即可得到消费的Euler方程式(4.1.8)。
假定经济是由许多家庭组成的,每个家庭没有差别,因此称为代表性家庭。通过分析代表性家庭的最优化行为,可以研究宏观经济变量的运动。假定产品市场与要素市场服从完全竞争,家庭计划的期间为无限长,不考虑人口增长,家庭的人数标准化为1,试图求解以下问题:
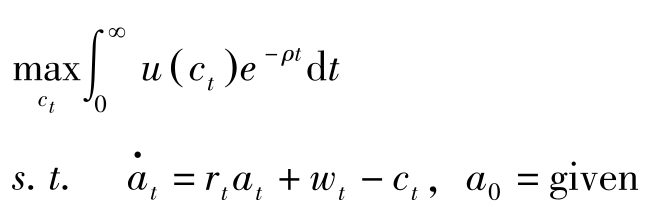
其中 c t 表示家庭的消费, u ( c t )表示瞬时效用, a t 表示 t 期期初资产存量, r t 表示利息率, w t 表示工资, ρ 表示主观偏好率;瞬时效用函数 u ( c t )满足 u′ ( c t )>0与 u ″ ( c t )<0。假定家庭对由市场决定的劳动工资率与资本租金能完全预知,在最大化自身效用时将它们视为既定。
构造Hamilton函数 H = u ( c t )+ q t ( r t a t + w t -c t ),则最优化的必要条件为:
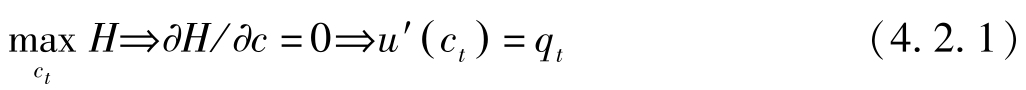
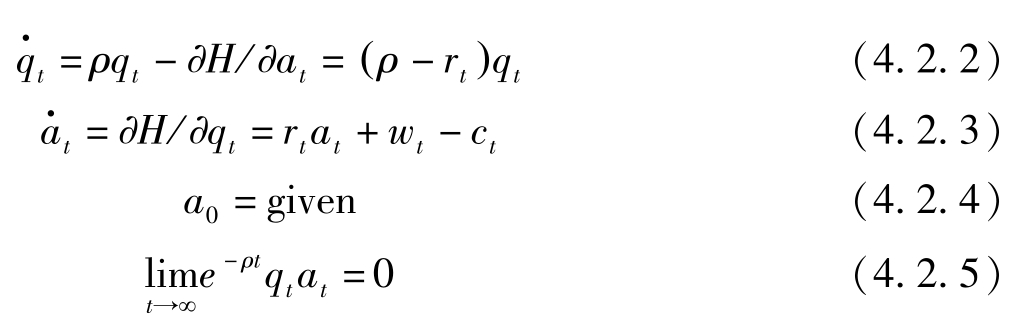
下面推导消费的运动方程。
(4.2.1)两边取对数后对时间求导并利用(4.2.2)有:
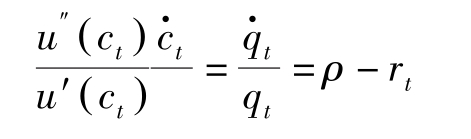
记
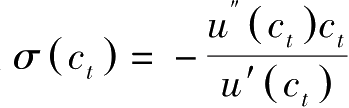 ,它是效用函数的曲率,更精确地说,它等于边际效用关于消费的弹性,也等于消费的瞬时替代弹性。
,它是效用函数的曲率,更精确地说,它等于边际效用关于消费的弹性,也等于消费的瞬时替代弹性。
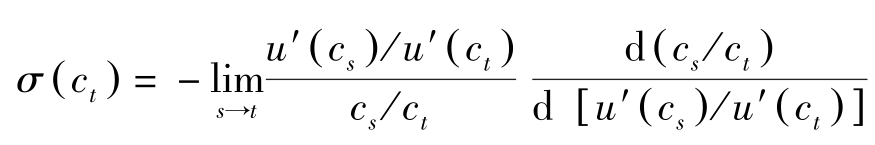
因而消费的Euler方程可表示为:

下面看一下横截性条件(4.2.5)式的经济学含义。先看离散型的情况。
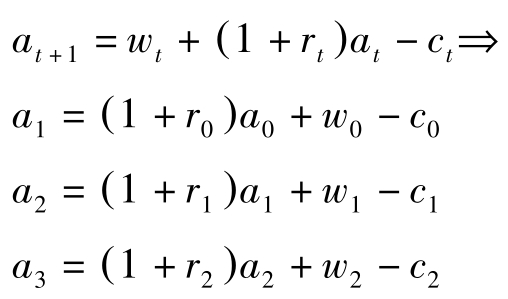
把以上三个式子合起来有:
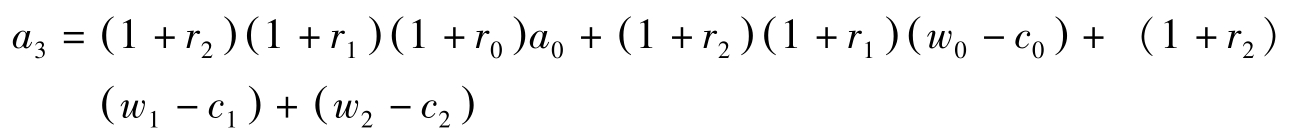
两边同除以 R t ≡(1+ r t )…(1+ r 1 )(1+ r 0 )有:
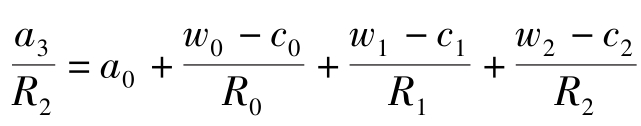
考虑到 T -1期为止时有:
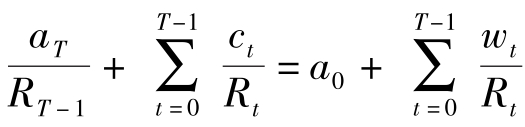
上式左边为终期资产与各期消费的贴现值,它等于右边的期初资产加各期工资收入的贴现。
对于有限期界的离散时间问题,效用最大化要求
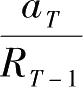 =0,即终期资产的现值为0。否则的话,资产还可继续被用来消费,效用还可以继续提高。
=0,即终期资产的现值为0。否则的话,资产还可继续被用来消费,效用还可以继续提高。
对于无限期界的离散时间问题,约束条件变为:
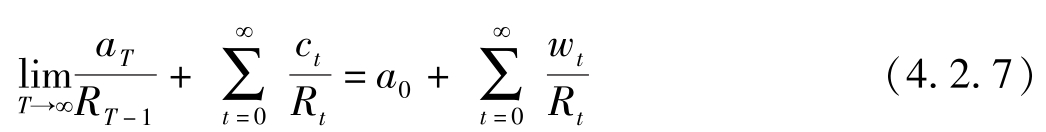
若
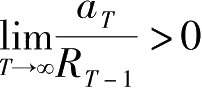 ,则
,则
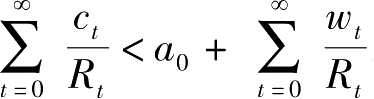 。这表明初期资产与工资收入的现值未被完全消费掉。效用最大时,必有
。这表明初期资产与工资收入的现值未被完全消费掉。效用最大时,必有
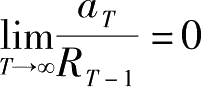 ,也即必有:
,也即必有:

上式称为No-Ponzi-Game condition。
下面讨论连续时间、无限期界的情形。
与(4.2.7)式对应的式子为:
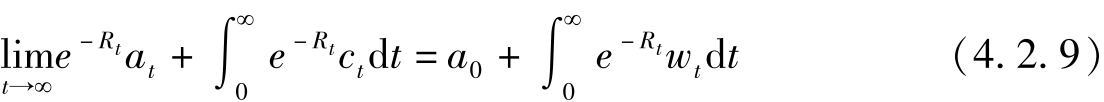
其中
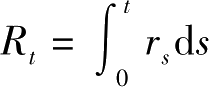 为累积利息率。左边第一项极限符号后面为
t
期持有的资产的现值,第二项为终生消费的现值,右边第二项为终生工资收入的现值。欲使效用最大化,一个必要条件就是必须满足No-Ponzi-Game condition,也即
为累积利息率。左边第一项极限符号后面为
t
期持有的资产的现值,第二项为终生消费的现值,右边第二项为终生工资收入的现值。欲使效用最大化,一个必要条件就是必须满足No-Ponzi-Game condition,也即
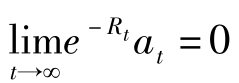
下面证明这一条件与横截性条件(4.2.5)式即
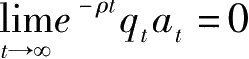 是等价的。
是等价的。
由(4.2.2)知,
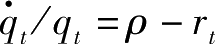 ,因此
,因此
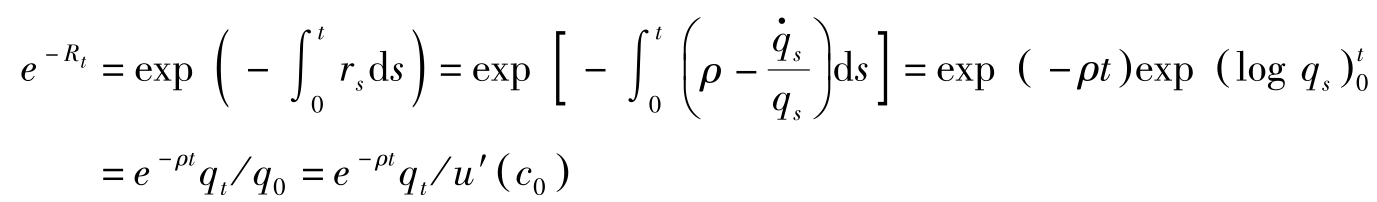
上式中, q 0 = u′ ( c 0 )>0[见(4.2.1)式]。故
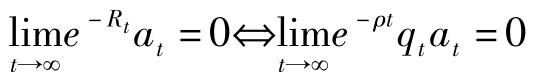
企业的生产函数假定为一次齐次的,或称规模收益不变,即
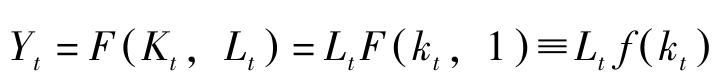
其中 f′ ( k t )>0; f″ ( k t )<0。
利润最大化导致:
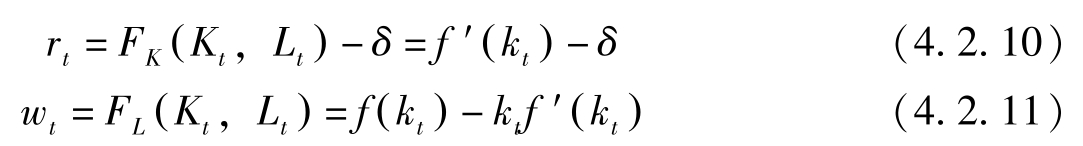
这里 δ 为资本折旧率。
假定生产要素充分就业;经济是封闭的;没有政府、货币与债券。
产品市场均衡式为:

资产市场均衡式为:

假定家庭把预期的 r t , w t 的序列值看作已知去最大化自己的效用,企业也把它们看作给定去最大化自身的利润。假定预期是充分的,即预期的 r t , w t 的序列值与实现的值是一致的。
下面看一下家庭预算约束与产品市场均衡式之间的联系。
由(4.2.13),家庭预算约束可改写为:
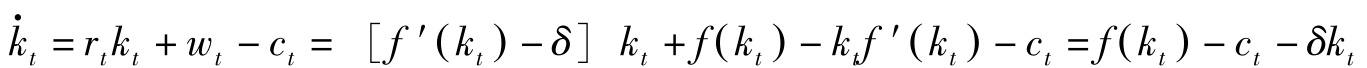
可见,家庭的预算约束与产品市场均衡是一回事。因此4.2.1至4.2.3所研究的经济的基本动力学体系可归结为:
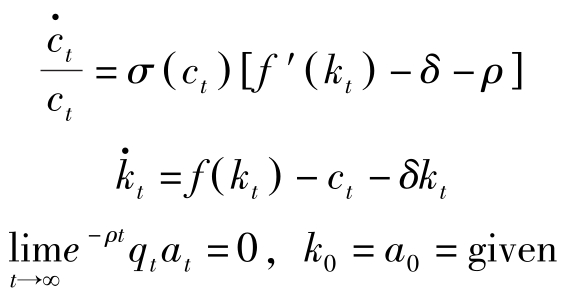
满足该体系的( k t , c t )的路径称为完全预见竞争均衡路径。
考虑下面的最优增长问题:
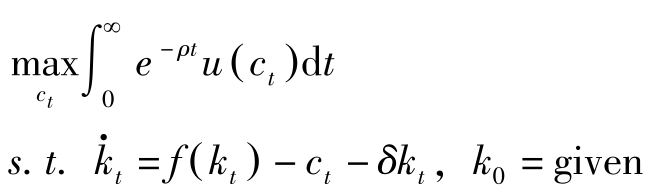
由于产品市场均衡式与家庭预算约束式是一致的,最优增长问题与完全预见竞争均衡的解也是一致的。
下面利用位相图分析该问题的基本动力学体系。
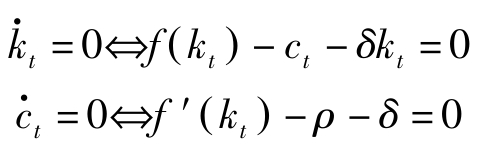
图4-1中,
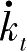 =0即
c
t
=
f
(
k
t
)
-δk
t
的形状呈倒“U”形;
=0即
c
t
=
f
(
k
t
)
-δk
t
的形状呈倒“U”形;
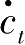 =0是一条垂直的直线。在
=0是一条垂直的直线。在
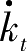 =0线的下方,
=0线的下方,
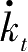 >0,表示随着时间的持续,人均资本要增加;
>0,表示随着时间的持续,人均资本要增加;
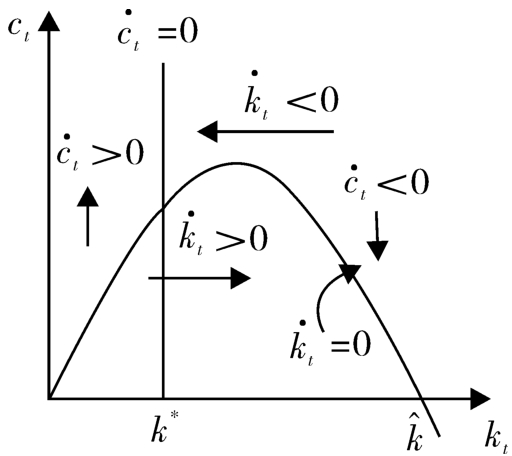
图4-1 C 与 K 的动力学
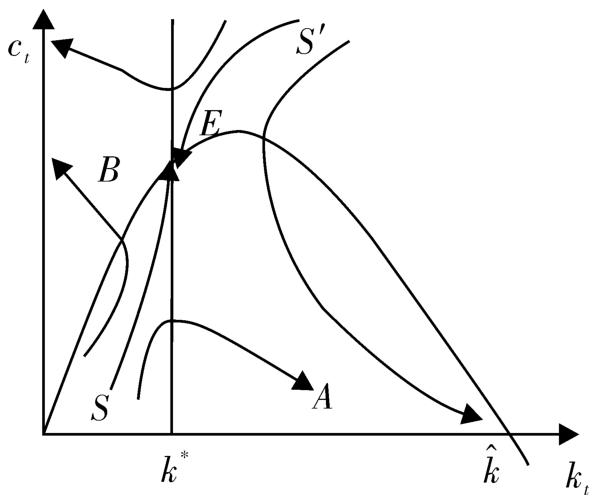
图4-2 C 与 K 的不同运动路径
在该线的上方,
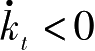 ,表示随着时间的持续,人均资本要减少;在
,表示随着时间的持续,人均资本要减少;在
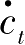 =0线的左边,
=0线的左边,
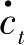 >0,消费要增加;在该线的右边,消费则要减少。经济在各区域的运动方向如图4-1 所示。存在唯一的鞍点路径
SS′
收敛到稳态均衡点
E
(如图4-2所示)。
>0,消费要增加;在该线的右边,消费则要减少。经济在各区域的运动方向如图4-1 所示。存在唯一的鞍点路径
SS′
收敛到稳态均衡点
E
(如图4-2所示)。
下面我们要说明,最优路径 SS′ 是唯一的, SS′ 以外的其他路径均非最优路径,因为它们都不能满足最优路径的必要条件。
SS′
下方的路径如路径
A
终将到达横轴的
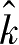 点,这样的路径会违反TVC。因为:
点,这样的路径会违反TVC。因为:
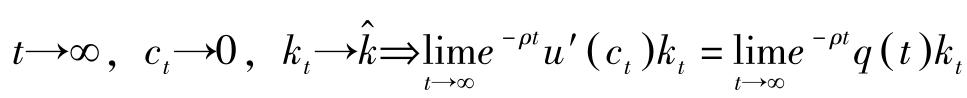
令 x t = e -ρt q ( t ) k t ,则
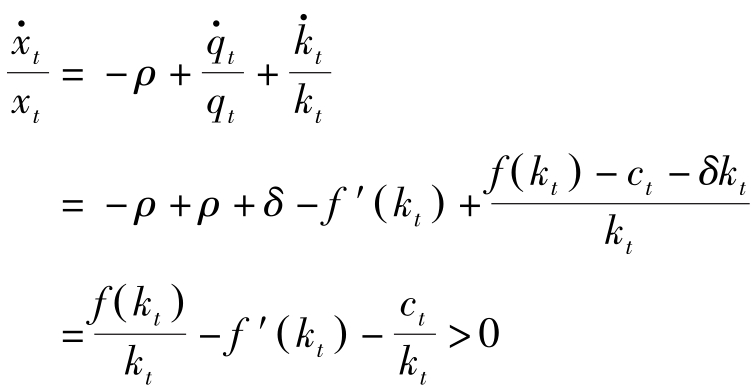
最后一个不等式成立是因为不等式左边的极限值
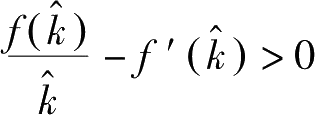 (因
f
凹)。故
(因
f
凹)。故
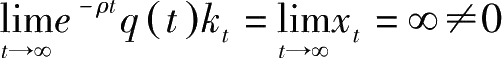 ,违反TVC。
,违反TVC。
再看 SS′ 上方的路径,如路径 B ,由于
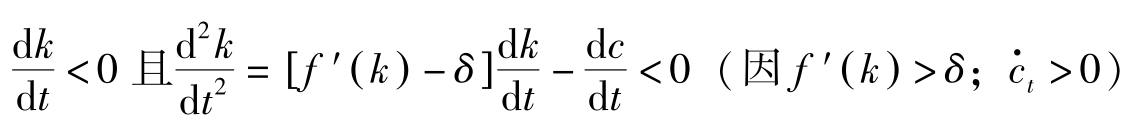
该路径上 k 加速减小,经济将在有限的时间内到达纵轴。一旦到达纵轴, k t 变为0,产量 f ( k t )也变为0,没什么可消费的了,消费也只好跳到0。但作为最优解必要条件的消费的Euler方程要求消费连续变动。因此该路径违背消费的Euler方程,从而也不是最优路径。
我们可以在 k = k ∗ , c = c ∗ 附近对基本动力学体系进行线性近似:
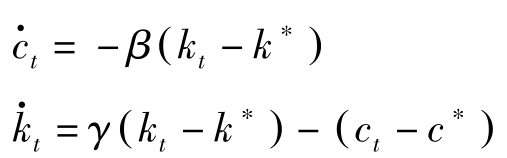
其中 β ≡ -f″ ( k ∗ ) c ∗ σ ( c ∗ )>0; γ ≡ f′ ( k ∗ ) -δ 。因此
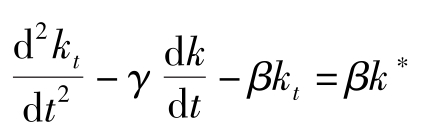
其特征根一正一负,令负根为 μ ,则 k t 的解为: k t = k ∗ +( k 0 -k ∗ ) e -μt 。
前述模型中没有政府,现在引入政府。政府发行债券 b ,征收一次性总赋税(Lump-sum tax) τ ,支出 g 。
政府预算约束:
流量约束:

跨期预算约束:

其中
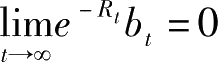 ,即假定满足No-Ponzi-Game condition。
,即假定满足No-Ponzi-Game condition。
家庭预算约束:

让(4.4.3)减去(4.4.1)可得:
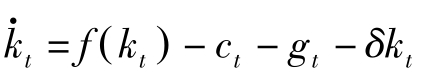
此即商品市场均衡式。因此,含有政府部门的动力学体系可归结为:
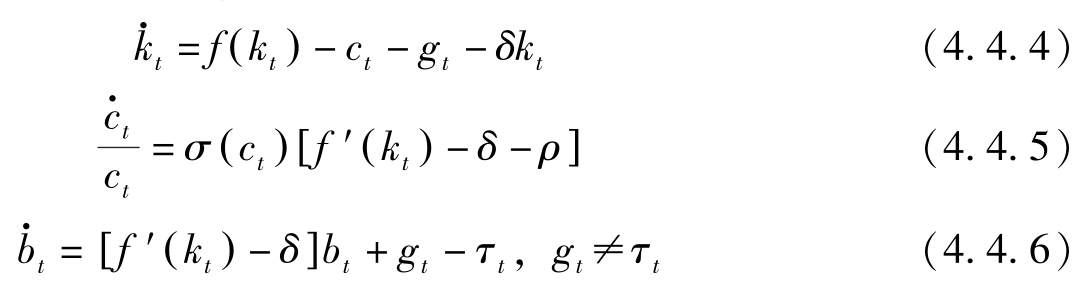
利用上述动力学体系,我们可以考察政府支出政策的调整对经济的影响。假定政府支出变动前为0,
t
=
t
0
时刻政府支出持久增加,这将引起
 线向下移动。如果这一政策未被预期到,经济将从原来的鞍点路径
SS′
上(比如原来在
A
点)向下跳到新的鞍点路径
S′S′
上(的B点),然后沿新的鞍点路径移向新的稳态均衡点
E′
(见图4-3)。消费、资本与政府支出的路径见图4-4。
线向下移动。如果这一政策未被预期到,经济将从原来的鞍点路径
SS′
上(比如原来在
A
点)向下跳到新的鞍点路径
S′S′
上(的B点),然后沿新的鞍点路径移向新的稳态均衡点
E′
(见图4-3)。消费、资本与政府支出的路径见图4-4。
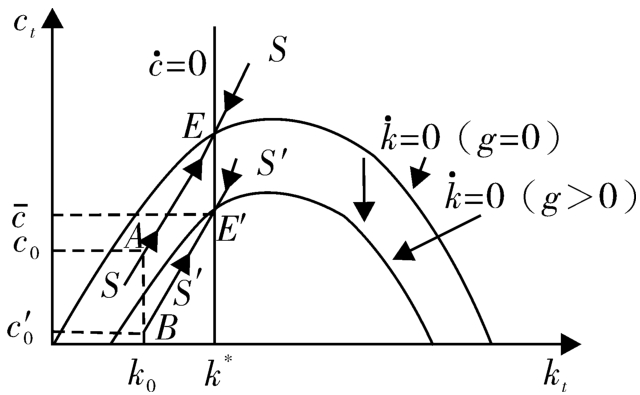
图4-3 政府支出增加(未被预期到)的效应
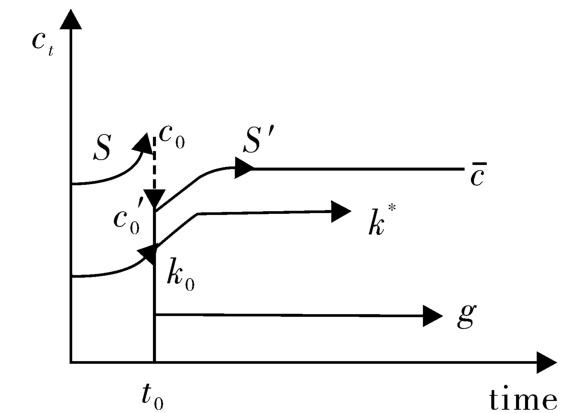
图4-4 消费、资本与政府支出的路径( g 增加未被预期到)
假定政府支出的变动被预期到。比如在 t = t 0 时刻宣布,再过 T 到 t = t 1 时刻,政府支出永久增加。
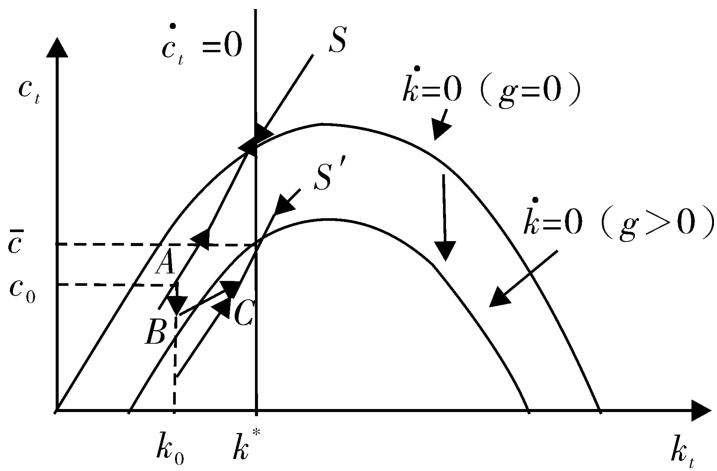
图4-5 政府支出增加(被预期到)的效应
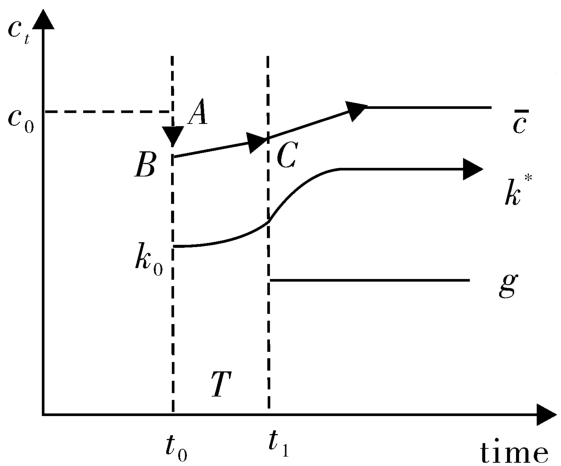
图4-6 消费、资本与政府支出的路径( g 增加被预期到)
消息宣布后,消费会向下小跳(从 A 到 B ),经济在原来的系统支配下向右上方运动,在 t = t 1 时刻来临时恰好运行到新的鞍点路径上( C 点)。然后在新系统支配下沿新鞍点路径向新稳态均衡点运动(见图4-5)。消费、资本及政府支出的路径如图4-6所示。
类似地,也可以分析经济初始处于原来的稳态均衡点的情况以及政府支出暂时增加的效果。
下面验证李嘉图等价命题。
李嘉图等价命题: 不管是通过一次性征税还是通过增发国债为政府支出融资,都不会影响家庭的决策。
我们知道家庭跨期预算约束为:
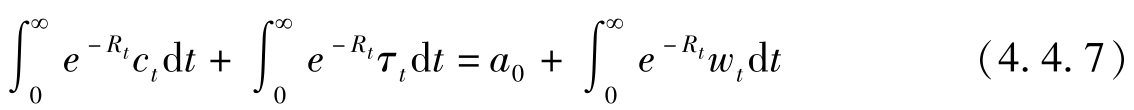
政府的跨期预算约束为:
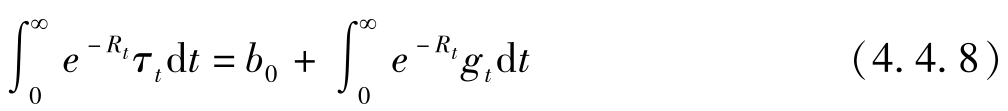
两式相减,注意到 a 0 = b 0 + k 0 ,我们有:
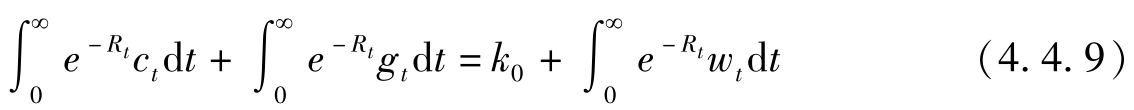
该式中既不含 τ t 也不含 b t ,因此政府融资方式不影响家庭决策。
这也可从其动力学体系(4.4.4)、(4.4.5)与(4.4.6)来分析。稳态的人均资本存量由下式决定(见4.4.5):
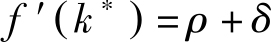
消费由(4.4.4)决定:
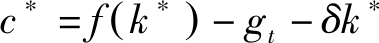
因此,消费与资本的决定均与政府是征税还是发债无关,不过政府支出会影响消费。