下载掌阅APP，畅读海量书库
立即打开
前一章的分析只考虑了离散时间、有限期界的动态最优化问题。但经济学中经常会遇到连续时间、无限期界的动态最优化问题，而且效用函数与状态运动方程往往采取某种特殊形式，环境约束条件也不起作用。本章考虑这样的问题，作为离散时间、有限期界的动态问题的延伸，我们将类似地给出连续时间、无限期界的动态问题的最大值原理、动态规划解法以及变分法。
具体地，本章我们将考虑如下问题：
(P AM )
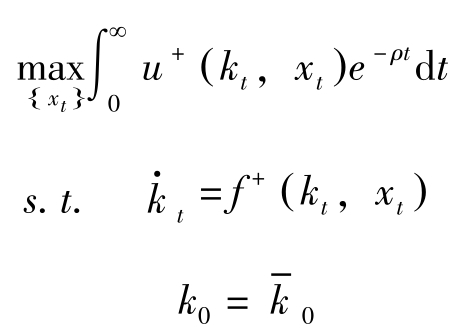
考虑上述问题的原因之一是这种问题在技术处理上比较简单。较之于离散时间且各函数中明确含有时间变量的情形，这种连续时间且函数中不明确含有时间变量的情形其结果更简单。如最大值原理中的Hamilton 动力学，在离散时间的场合用差分方程来表达，而在连续时间的场合则可用微分方程式表示。一般而言，微分方程式的处理较之差分方程要容易一些。特别是在讨论外生变量的变动对最优路径的影响时，微分方程中的各种技巧（如位相图）用起来更顺手。
第二个原因是，对许多经济主体而言，规划期为无限长这一想法也比较自然。企业要持续经营，把规划期间看作无限长既自然又合理；家庭是一个绵延不绝的家系，某一时点的家庭做决策时会一并考虑其子孙的效用。这样，尽管个人的寿命有限，但家庭的最优决策实际上是要让整个家系的总效用在无限长的期间内达到最大。
在规划期为无限长的情况下，终期的效用的现值 ν （ T ， k T ）这一项就自然而然地消失了，横截性条件也随之发生变化。我们将转为考虑无限远期的资产的现在价值的极限趋于零。
高级宏观经济学（Advanced Macroeconomics）实际上主要讨论的就是上述问题（P AM ）。
对于如下离散时间的变分法问题：
(P V )
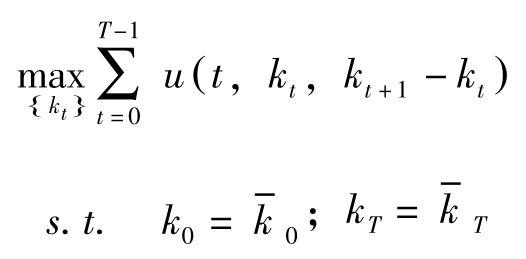
其对应的Euler差分方程式为：
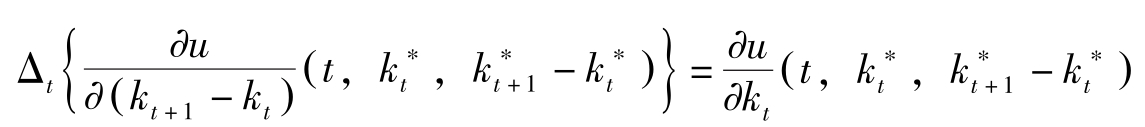
其 中，
，而
x
t
≡
k
t
+1
-k
t
。
注意到离散时间场合的
x
t
≡
k
t
+1
-k
t
对应于连续时间的
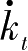，上述离散时间的动态优化问题对应于下述连续时间的问题：
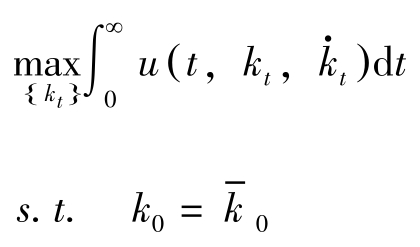
Euler差分方程式对应于Euler微分方程式：
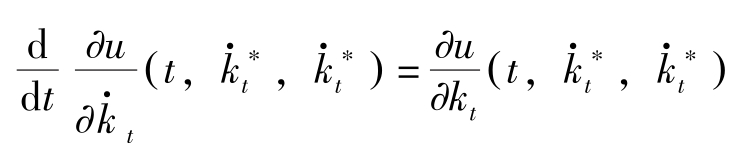
现在
，因此Euler微分方程式为：
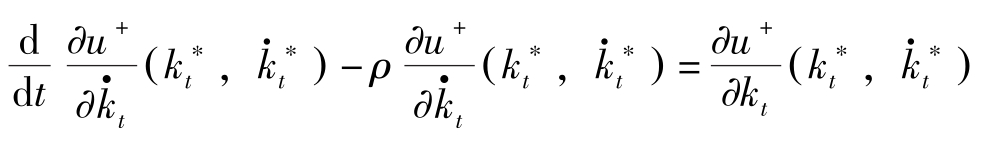
考虑第2章中问题（P）的约束 g ≥0不起作用的离散时间动态优化问题
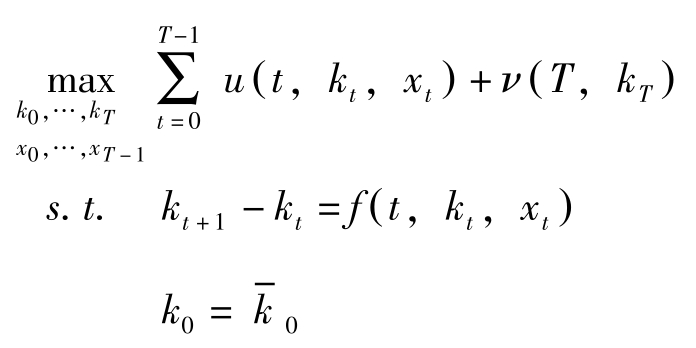
在连续时间的场合其对应于如下问题：
(P c )
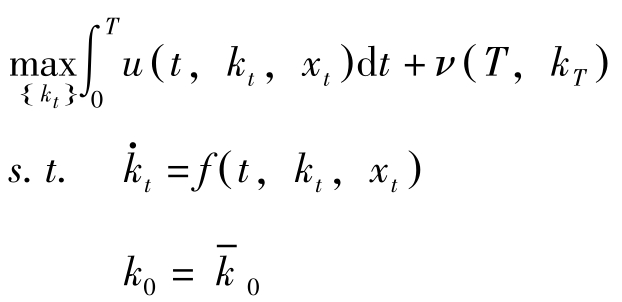
建立Hamilton函数
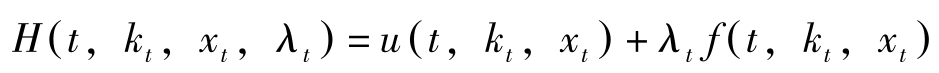
对于（P
c
）的最优解
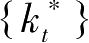，存在
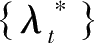使得以下四个条件成立（第2章定理2中没有函数
g
的情况）：
（1）Hamilton函数最大化：
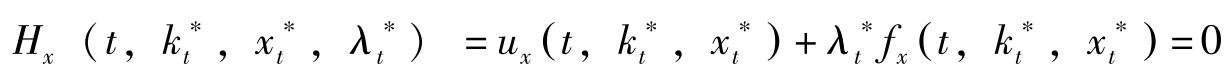
（2）Hamilton动力学：
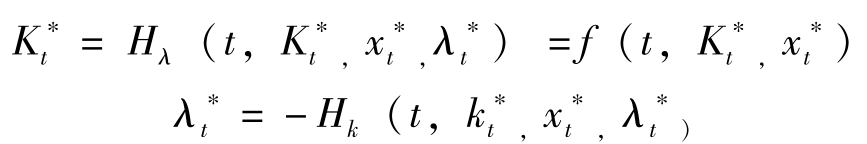
（3）横截性条件（TVC）：
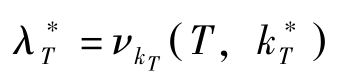
（4）期初条件：
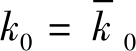
实际上在连续时间的场合，（1）Hamilton函数最大化可以进一步地改写为更强的条件：
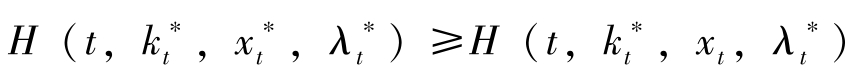
具体理由超出本书讨论范围，可参见Luenberger，1979，第十一章。
我们考虑 u （ t ， k t ， x t ）= u + （ k t ， x t ） e -ρt ， f （ t ， k t ， x t ）= f + （ k t ， x t ）的情形。
令
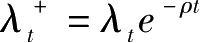，重新定义Hamilton函数如下：
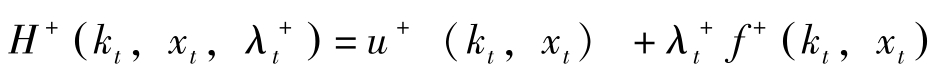
显然
H
（
t
，
k
t
，
x
t
，
λ
t
）=
H
+
（
k
t
，
x
t
，
）
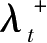e
-ρt
。于是有：
定理1：
假定问题（P
c
）中，
u
（
t
，
k
t
，
x
t
）=
u
+
（
k
t
，
x
t
）
e
-ρt
，
f
（
t
，
k
t
，
x
t
）=
f
+
（
k
t
，
x
t
）。若
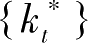与
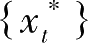是最优解，则存在
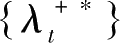，使以下四个条件成立：
（1）当期价值Hamilton函数最大化：
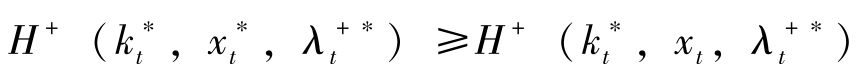
（2）当期价值Hamilton动力学：
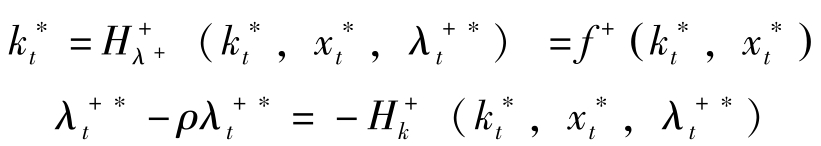
（3）横截性条件（TVC）：
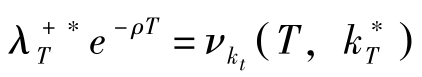
（4）期初条件：
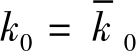
现在考虑连续时间、无限期界的动态最优化问题（P AM ）。显然，最大值原理中的条件（1）、（2）与（4）不变，这可以从离散时间的最大值原理的推导过程看出来。但横截性条件（3）发生了变化。
如何变化呢？我们认为，对于一个最优的计划而言，在计划期间的最后，计划者的剩余资产的现值必将为0。如果不为0，这些资产仍可被用于消费，增大效用。这样的话，目前的计划也就不是最优的了。因此横截性条件（3）可改写为：
（3 ∗ ）横截性条件（TVC）：
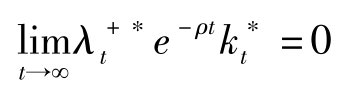
定理1中的问题对应的离散时间问题为：
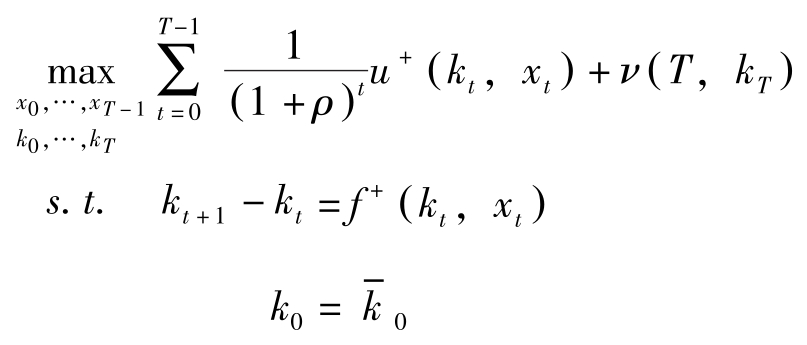
该离散时间问题的状态评价函数定义为：
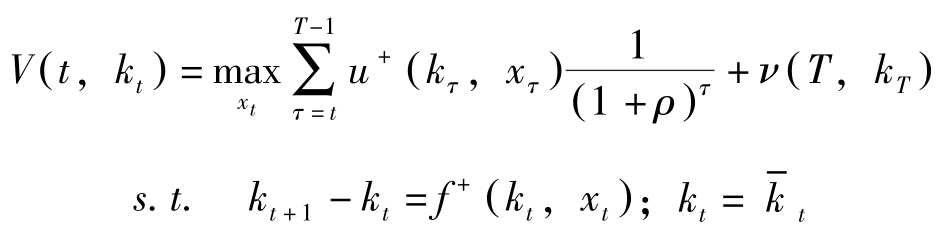
定理1中问题的状态评价函数为：
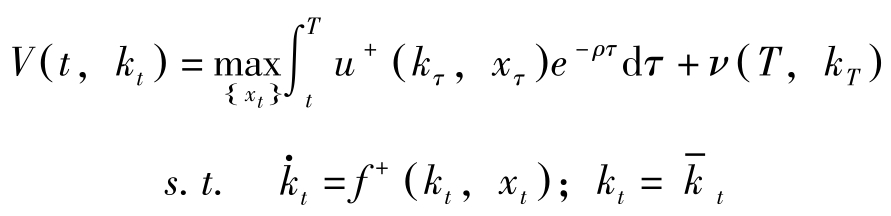
离散时间问题的Bellman方程式为：
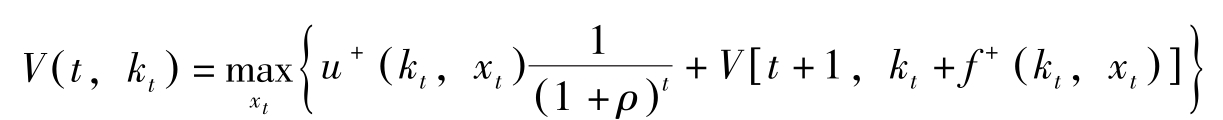
期间的长度若从1变为 δ 则Bellman方程变为：
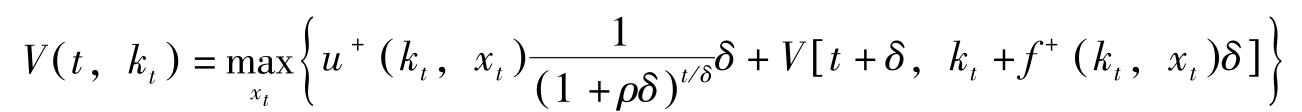
现在 V （ t ， k t ）关于 t ， k t 连续可微，近似地
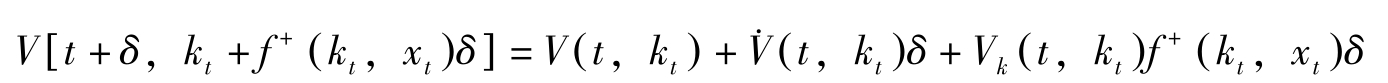
其中
≡
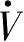∂V/∂t
。将上式代入Bellman方程有：
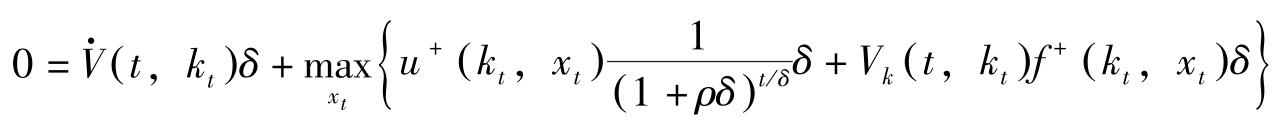
上式右边第一项与 x t 无关，故可以放在最大值符号的外面。
期间的长度 δ 趋于0时即为连续的情况。两边同除以 δ 然后求极限有：
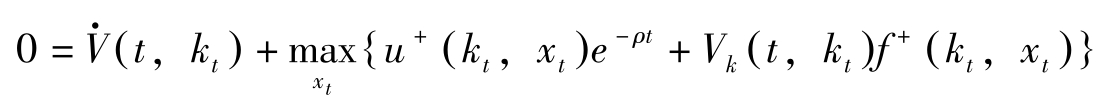
即
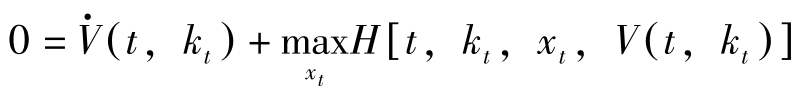
这里， H ［ t ， k t ， x t ， V （ t ， k t ）］≡ u + （ k t ， x t ） e -ρt + V k （ t ， k t ） f + （ k t ， x t ）。上式称为Hamilton-Jacobi方程式。
例：考虑下述离散时间的优化问题：
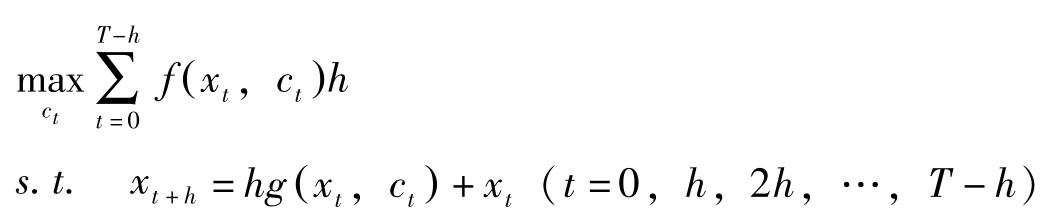
其中 T 为计划期间， x t ， c t 分别为状态变量与控制变量， x 0 = x -0 。
（1）建立拉格朗日函数，给出最优解的一阶条件。
（2）给出对应的连续时间问题及最优解的必要条件即最大值原理。
（3）采用动态规划的方法求解上述离散问题。
（4）计划期界
T
趋于无穷大时，引入贴现因子
，其中
ρ
为贴现率。问题变为：
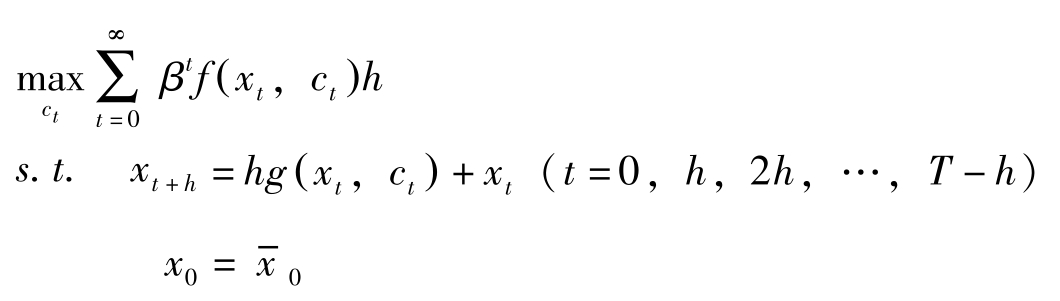
给出最优解的必要条件。
（5）在时间连续、无限期界的情况下，问题（4）变为：
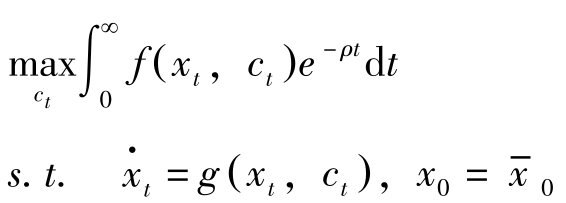
给出最优解的必要条件，即最大值原理。
解：（1）拉格朗日函数
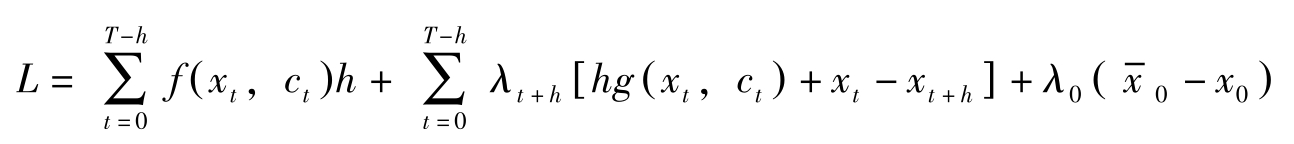
一阶条件：
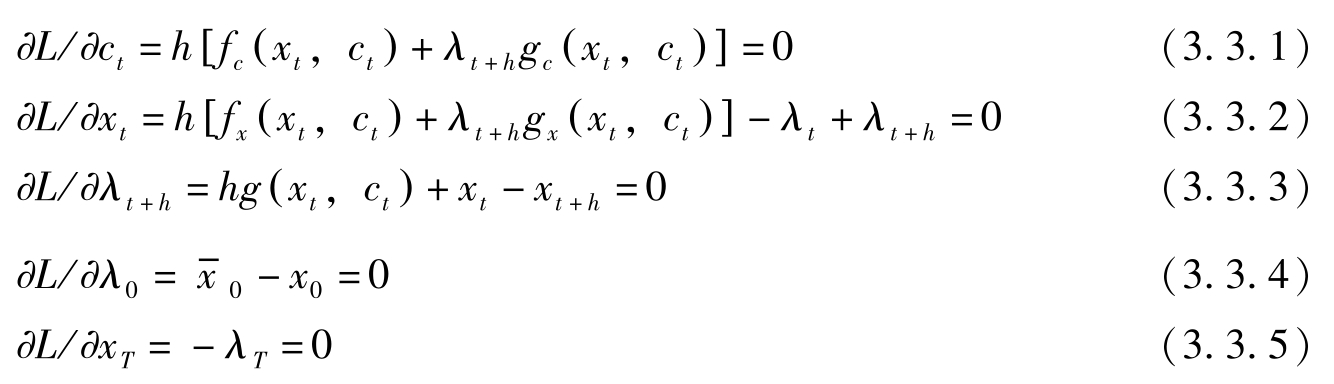
以上各式中， t =0， h ，2 h ，…， T-h 。
（2）先看一下微分方程式与差分方程式的联系。对于差分方程式
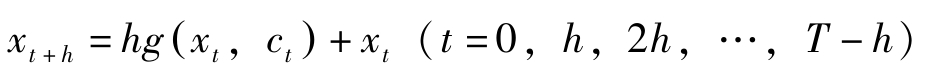
通常时间间隔假定为1。在连续时间的情况下 h →0约束条件对应地变为：
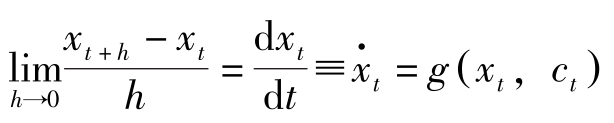
目标函数对应地变为
。
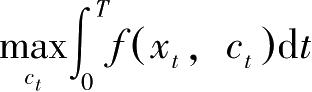因此连续时间的问题为：
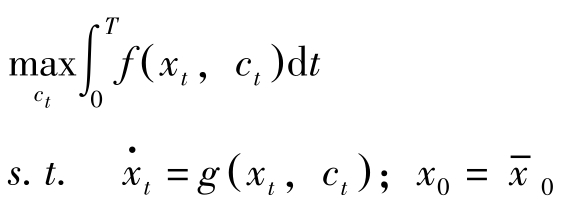
构造Hamilton函数 H = f （ x t ， c t ）+ λ t g （ x t ， c t ），则必要条件变为：
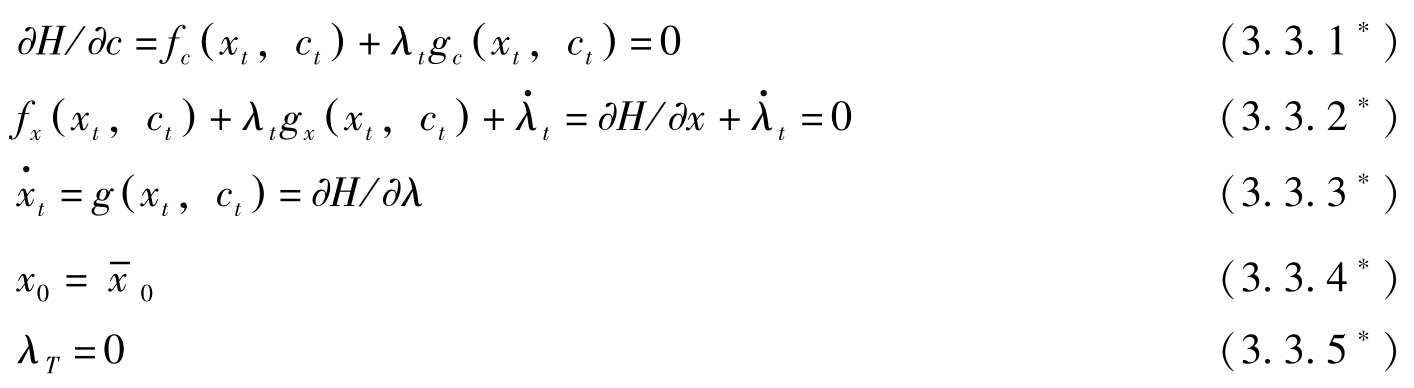
这就是连续时间、有限期界的最大值原理。
（3）定义
V
（
x
t
）=
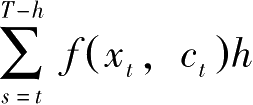，则有以下的Bellman方程式：
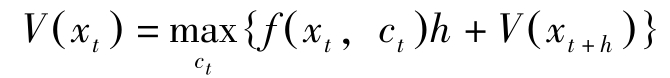
关于 c t 最大化要求
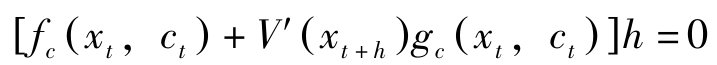
Bellman方程式两边对 x t 求导，有
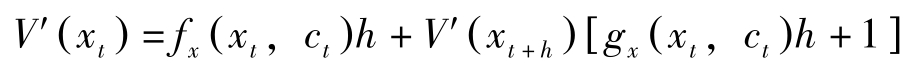
令 V′ （ x t ）= λ t ，则以上两式分别变为：
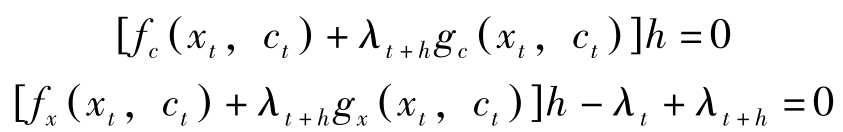
这与拉格朗日乘子法的（3.3.1）与（3.3.2）相同。
（4）拉格朗日函数：
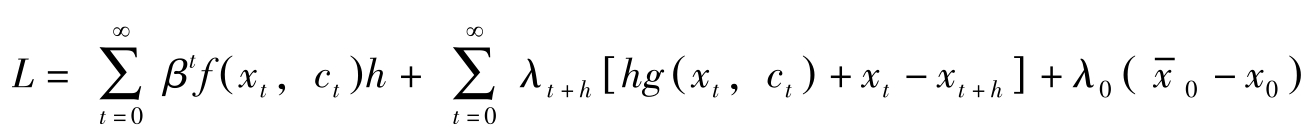
一阶条件的前四条与有限期界的情况相同，即
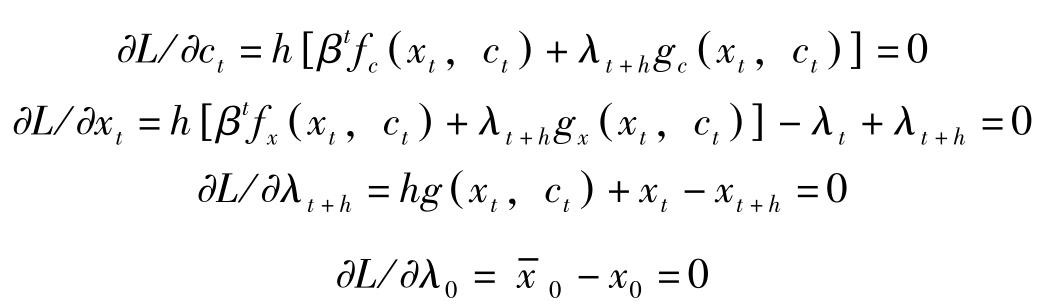
但横截性条件发生了变化，之前有限期界的场合要求状态变量的影子价格 λ T =0，现在我们无限期界的场合要求状态变量的影子价值的现值，即 λ t x t 趋于0，也即要求
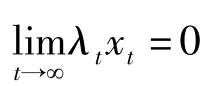
这一条件和第4章的No-Ponzi-Game condition 相一致，在那里我们将能更好地理解该条件的含义。
（5）构造Hamilton函数
=
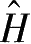f
（
x
t
，
c
t
）
e
-ρt
+
λ
t
g
（
x
t
，
c
t
），则必要条件变为：
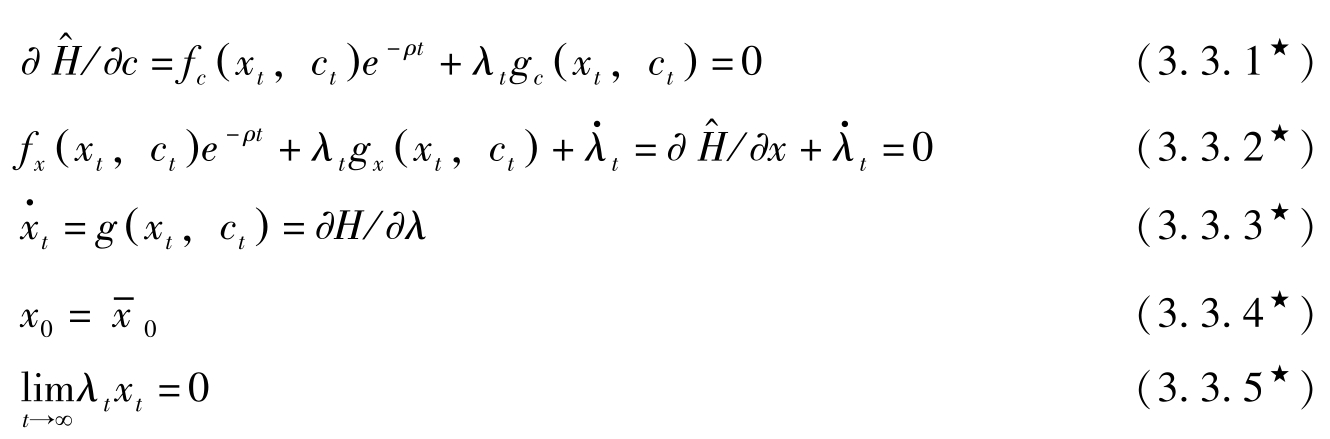
这就是连续时间、无限期界的最大值原理。
若令 H = f （ x t ， c t ）+ q t g （ x t ， c t ），其中 q t = λ t e ρt 表示状态变量影子价值的当期价值， H = H ^ e ρt 。则最优解的必要条件可转换为：
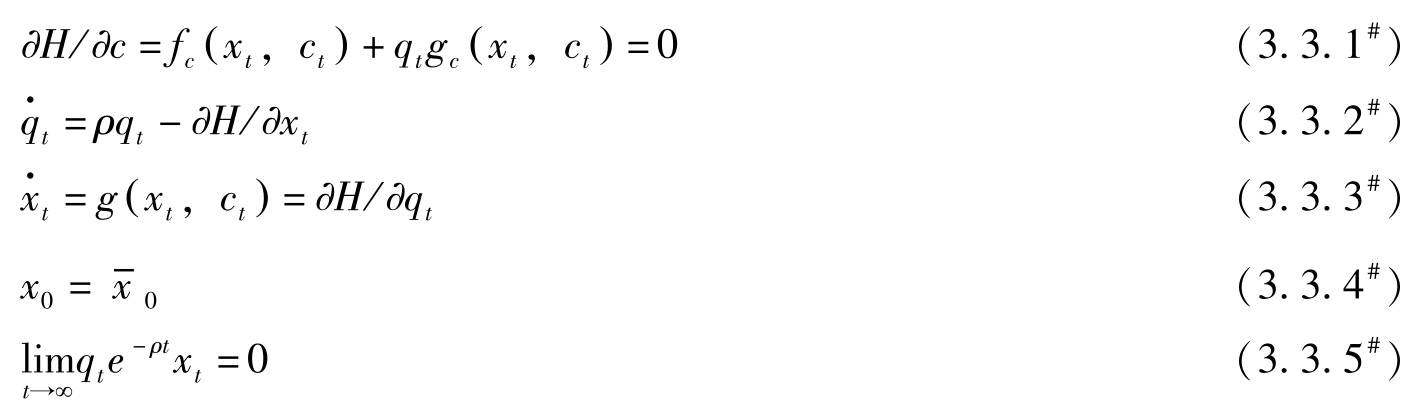
下面我们利用高级宏观经济学中常见的动态优化问题证明最大值原理。
A. 有限期界、不含贴现
家庭在其资产约束下，寻求消费的最优时间路径以最大化自己的终生效用，即
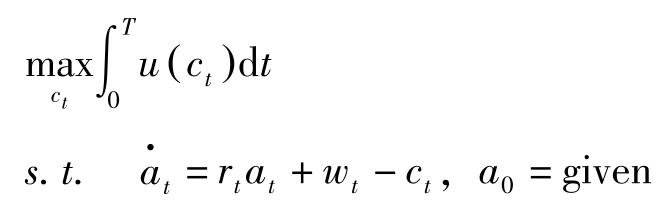
其中， T 为计划期界， c t 表示家庭的消费， u （ c t ）表示瞬时效用， a t 表示 t 期期初资产存量， r t 表示利息率， w t 表示工资。
上述问题是高级宏观经济学中最常见的问题。
记 H = u （ c t ）+ λ t （ r t a t + w t -c t ），则最优解的必要条件如下：
上述问题最优解的必要条件即为不含贴现、有限期界的最大值原理。
证明：
记
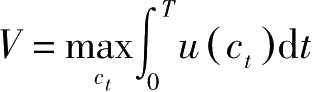。由原泛函
V
导出新泛函
Y
。
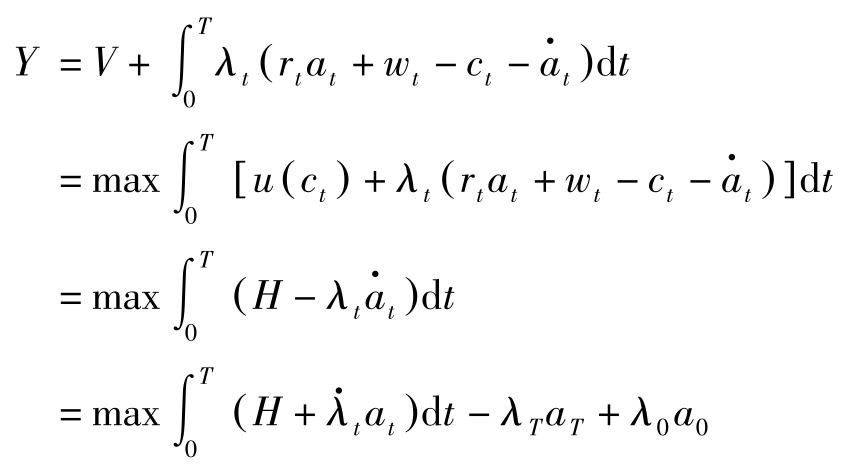
（A3）式可直接由 H = u （ c t ）+ λ t （ r t a t + w t -c t ）推出，即
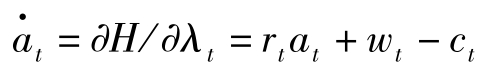
对于最优解 c ∗ （ t ）， a ∗ （ t ），它们的邻近路径分别记为
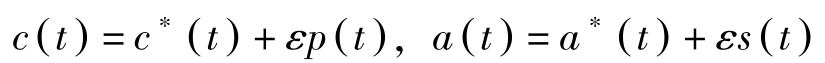
更进一步地，若 T 与 a T 均可变，则有：
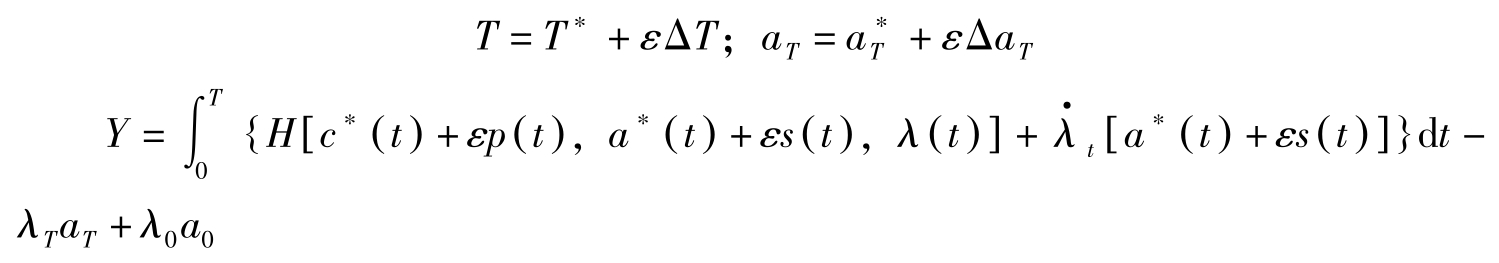
上式右边的第一项对 ε 求导有：
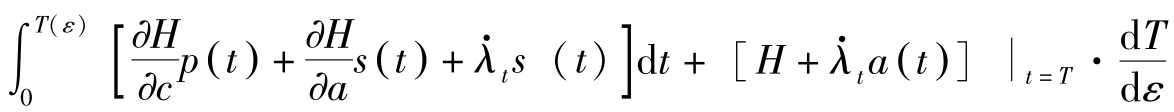
右边的后两项对 ε 求导有：
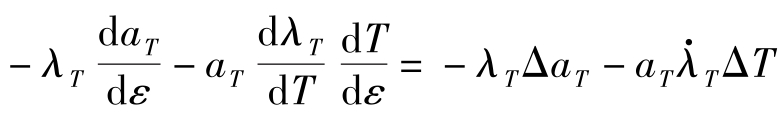
令d Y/ d ε =0则有：
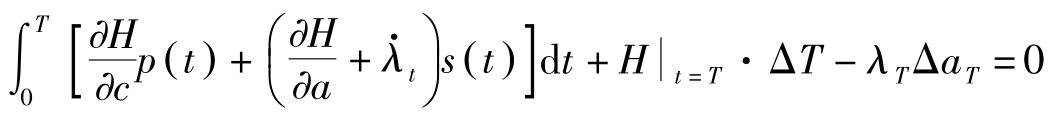
由于 p （ t ）， s （ t ）都是任意的，故（A1）式与（A2）式成立。
由上式积分项等于零可知一般性横截性条件成立，即
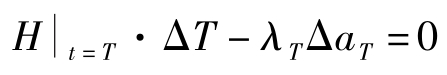
给定 T ，在 a T 可自由变动的前提下，一般性横截性条件意味着（A5）式成立，即 λ T =0，也即期终资产的影子价格的现值为0。
B.有限期界、含有贴现
考虑如下问题：
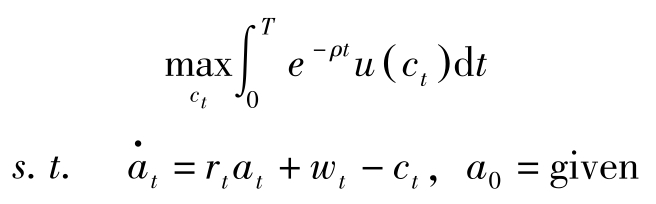
其中 ρ 为贴现因子。
构造Hamilton函数
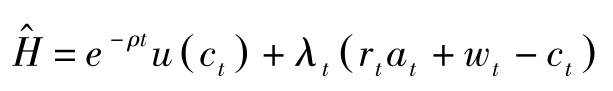
必要条件为：
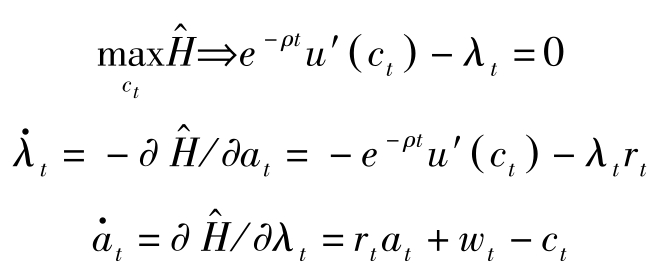
令 q t = λ t e ρt ，则 q t 表示资产的影子价格的当期值。定义Hamilton函数为：
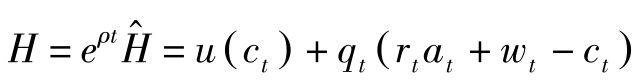
则可将最优解的必要条件归结为：
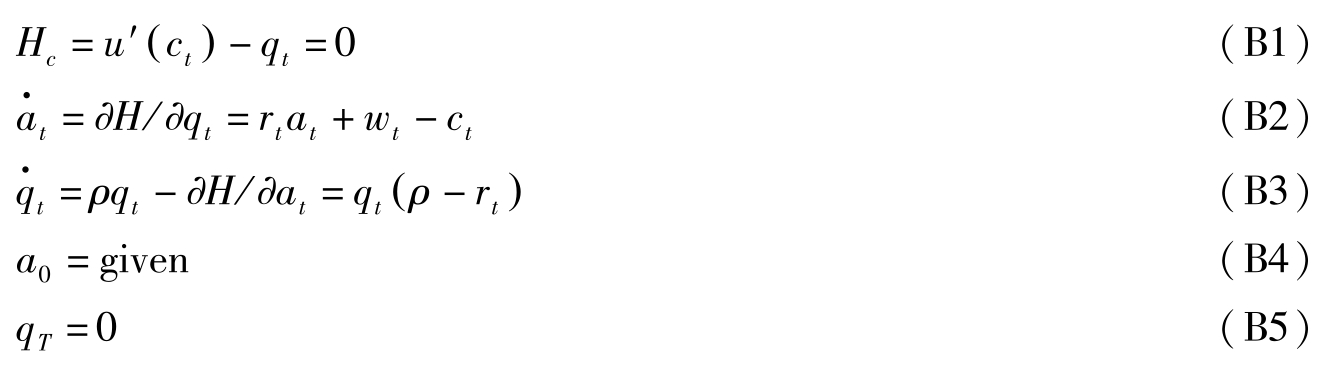
最后的（B5）式的经济学含义仍然是终期的资产影子价格为0。
C.无限期界、含有贴现
若计划的期界无限长，即考虑如下问题
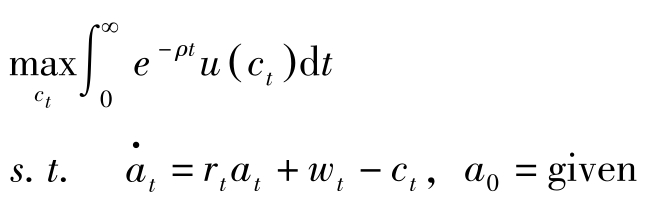
构造Hamilton函数 H = u （ c t ）+ q t （ r t a t + w t -c t ），则最优解的必要条件为：
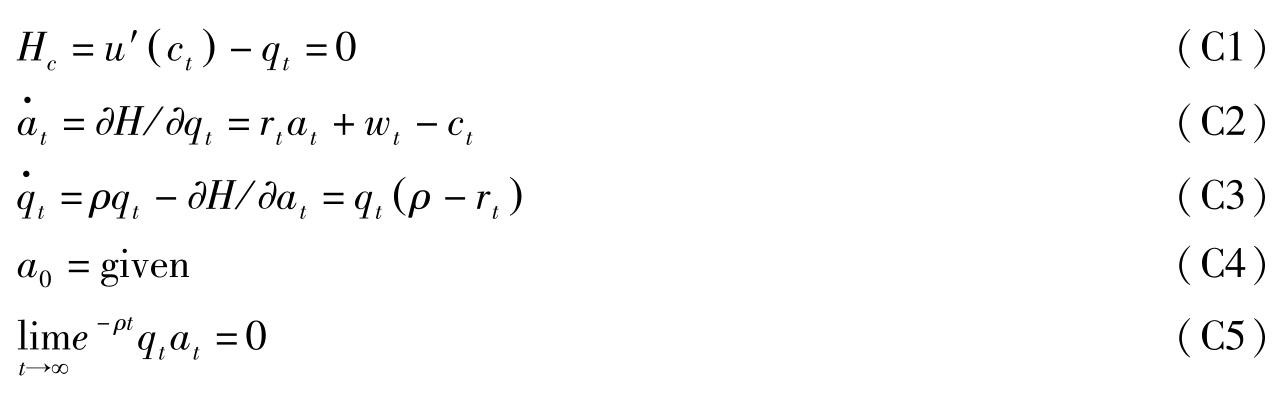
（C5）式称为横截性条件（TVC），其经济学含义是时间趋于无穷大时资产的影子价值（影子价格乘以资产数量）的贴现值应为0。否则表明资产未被完全消费掉，通过增加消费（这些资产），仍可增加效用，也就是说目前的解并非最优。