




前一章处理的问题只涉及一个时点,属静态最优化问题;现实中的诸多问题涉及多个时点甚至连续时间的资源分配,属动态最优化问题。本章讨论离散时间、有限期界的动态最优化问题及其解法,下一章我们将分析连续时间、无限期界的动态最优化问题。
本节介绍动态分析中最典型的问题及其三种解法(变分法、最大值原理与动态规划)的基本思想。
规划者要制订一个 T 期的计划,确定各期的消费与资本保有量,使计划期内效用达到最大,即
(P)
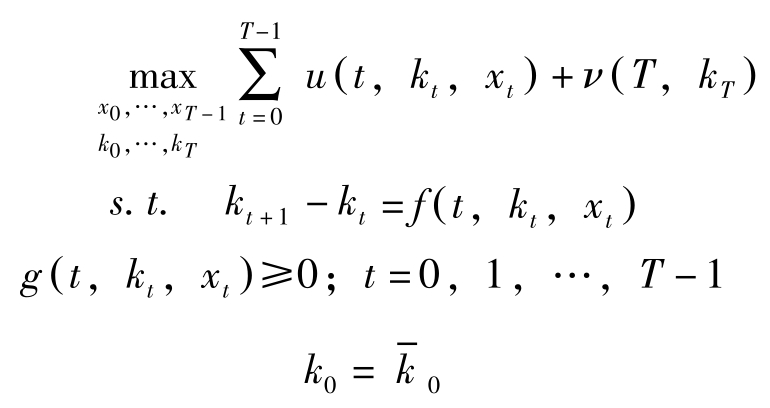
这是最典型的离散时间的动态问题。其中 x t 表示控制变量(消费), k t 表示状态变量(资产存量), T 表示计划的期间, u ( t , k t , x t )表示 t 期的效用, ν ( T , k T )表示期终残存资产的效用的现在价值。第一个约束是状态变量的运动方程,表示家庭资产的变动依赖于期初资产、利息率、支出额与收入额;然后是环境制约,如资产存量非负、劳动供给非负、消费需预付现金等约束;最后是期初条件。
变分法主要适用于求解这样的问题:约束条件 g ( t , k t , x t )≥0; t =0,1,…, T -1未起作用,且目标函数最大化的手段只依赖于状态变量的路径( k t +1 -k t = x t ),即求解下述问题:
(P V )
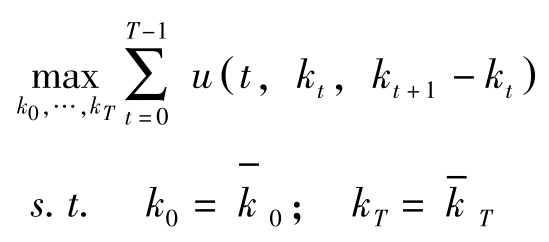
变分法通过引入微小的变化来推导最优解的性质,如著名的Euler差分方程式等。该方法的特点是直观、有效、易于理解。
运用最大值原理(Maximum Principle)求解时,并不把 t 看成历史时间,而是将其看作外生变量,也就是说,不是把 x t 与 k t 看作随时间变化的变量,而是将 x 0 , x 1 …, x T -1 ; k 1 ,…, k T 看成独立的变量,把状态方程与环境约束通通看成约束条件。将(P)看成静态问题(NLP),采用(NLP)的方法进行求解。
最大值原理的特点是以状态运动方程的拉格朗日乘数的形式引入共状态变量,动态问题与时间分离,Hamilton函数的使用与共状态变量的引入使最优条件的表达式简洁化。
动态规划方法则注重历史的时间推移,也就是说,运用动态规划解决的问题需要被一期一期地依次解决。
动态规划方法的特点是,基于状态变量导入价值函数,该函数能使各期的决定问题简单化。
以上三种方法相互补充,Euler方程、共状态变量与价值函数相互关联。
变分法常用来分析如下的离散时间问题:
(P V )
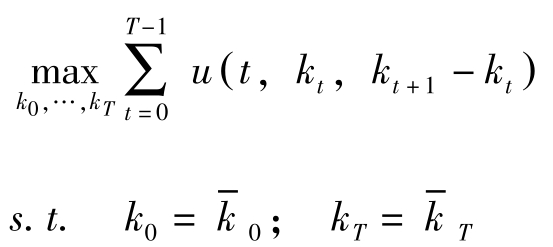
与典型问题相比,变分法讨论的问题没有环境约束,控制变量 x t = k t +1 -k t , k T 固定, u 连续可微。
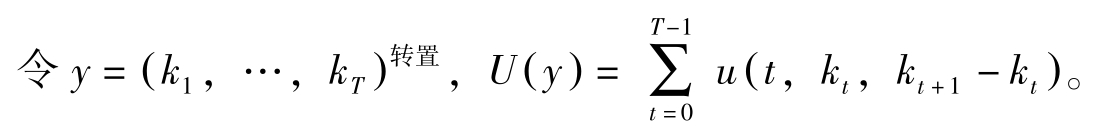
若
y
∗
为最优解,则
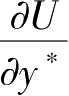 =0,即
=0,即
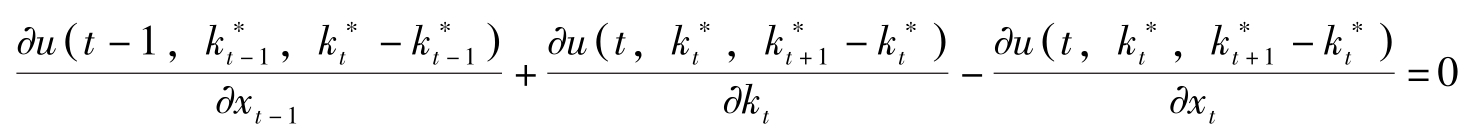
也即
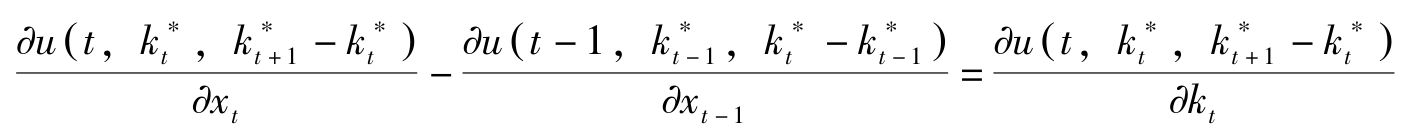
必须成立,其中 t =0,1,…, T -1。该式称为Euler差分方程式。
上述Euler差分方程式为二阶,因此若两个时点的 k t 确定了,比如 k 0 与 k 1 确定了, k t 的整个时间路径也就确定了。由于该问题给出了初始条件与终端条件,因此{ k t : t =0,1,…, T }的路径也就完全确定了。
采用如下记号:
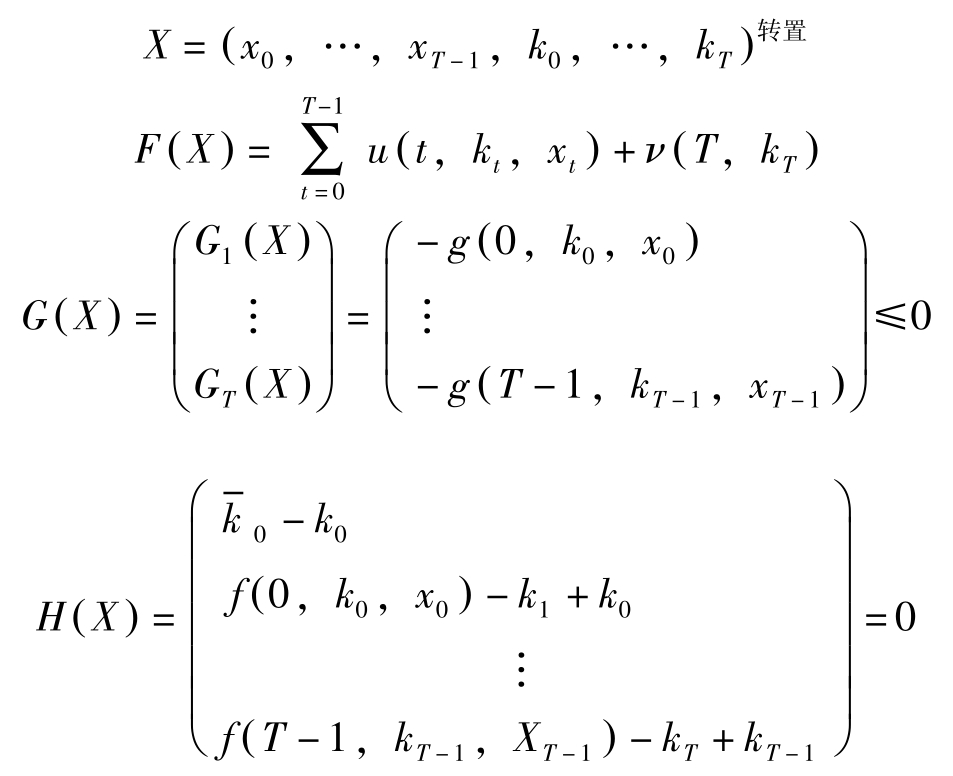
于是动态最优化问题(P)与下述混合型(NLP)相同:
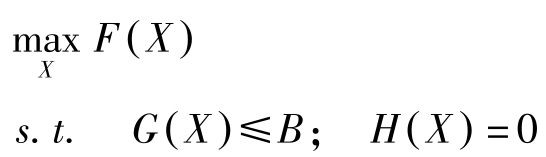
混合型(NLP)既含不等式约束也含有等式约束。因此,前一章中与混合型(NLP)对应的库恩塔克条件也适用于(P)。
定义:
若
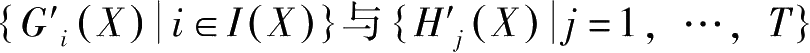 的行向量线性无关,则说
G
,
H
在
X
满足混合型(NLP)的正则条件。这里
I
(
X
)={
i|G
i
(
X
)=
B
i
}。
的行向量线性无关,则说
G
,
H
在
X
满足混合型(NLP)的正则条件。这里
I
(
X
)={
i|G
i
(
X
)=
B
i
}。
定理1: 假定 X ∗ 为混合型(NLP)的最优解, F , G , H 连续可微,且 G , H 在 X ∗ 满足正则条件,则存在 λ ∗ , ξ ∗ 使得:
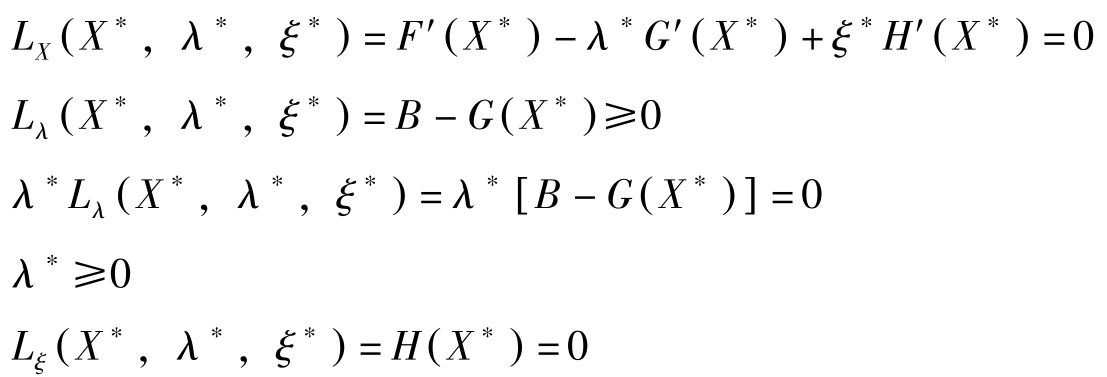
成立。其中 L ( X , λ , ξ )= F ( X )+ λ [ B-G ( X )]+ ξH ( X )。
定义:
记
I
(
X
)={
i|G
i
(
X
)=0},若
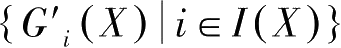 与
与
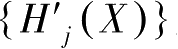 的要素向量线性无关,则称
f
,
g
在
X
满足动态问题(P)的正则条件。
的要素向量线性无关,则称
f
,
g
在
X
满足动态问题(P)的正则条件。
下面我们要证明:若 f , g 在最优解 X ∗ 满足动态问题(P)的正则条件,则混合型(NLP)的库恩塔克条件是最优解的必要条件。
首先构造拉格朗日函数
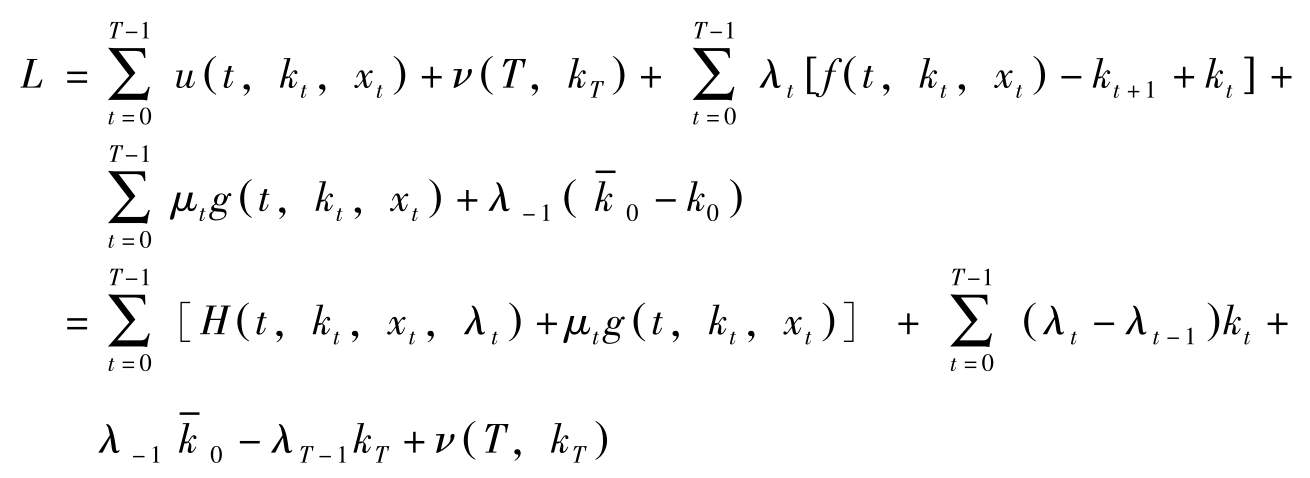
其中 H ( t , k t , x t , λ t )= u ( t , k t , x t )+ λ t f ( t , k t , x t )称为现值的Hamilton函数。因此,对于 t =0,1,…, T -1,库恩塔克条件如下:
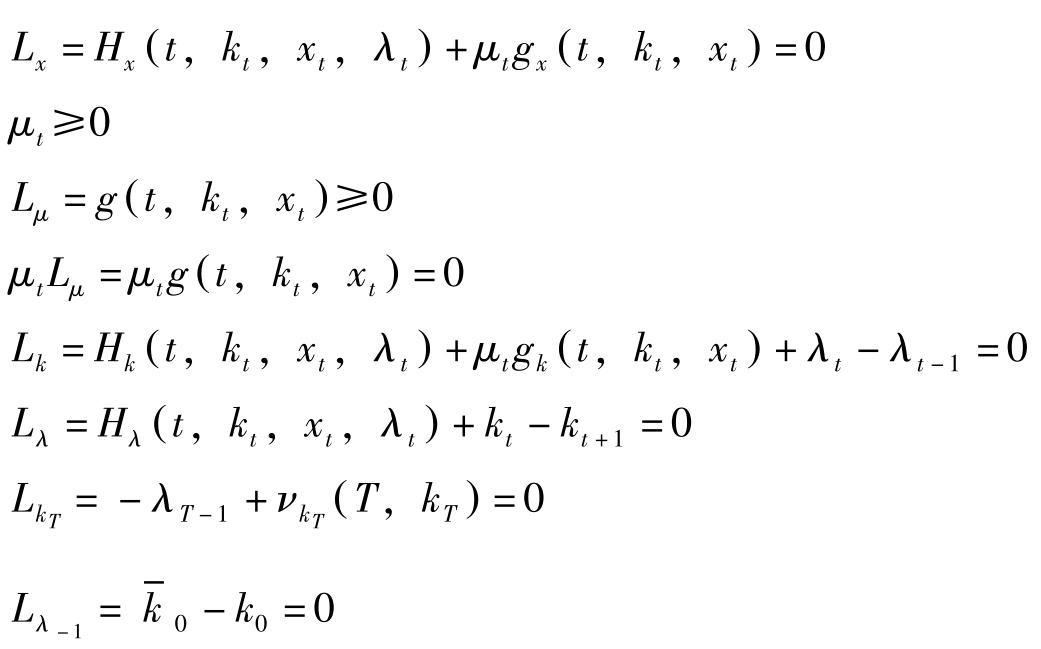
若
x
∗
是最优解,则存在{
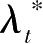 :
t
=0,1,…,
T
}与{
:
t
=0,1,…,
T
}与{
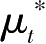 :
t
=0,1,…,
T
-1}使以上八式成立。
:
t
=0,1,…,
T
-1}使以上八式成立。
于是我们有下述定理:
定理2(最大值原理的必要性):
在问题(P)中,假定
u
,
ν
,
f
,
g
分别关于各独立变量连续可微,且
f
,
g
满足动态问题(P)的正则条件。若{
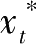 :
t
=0,1,…,
T
-1}与{
:
t
=0,1,…,
T
-1}与{
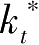 :
t
=0,1,…,
T
}是问题(P)的最优解,则存在{
:
t
=0,1,…,
T
}是问题(P)的最优解,则存在{
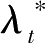 :
t
=-1,…,
T
-1}与{
:
t
=-1,…,
T
-1}与{
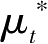 :
t
=0,1,…,
T
-1}使以下四个条件成立:
:
t
=0,1,…,
T
-1}使以下四个条件成立:
(1)Hamilton函数最大化的库恩塔克条件:
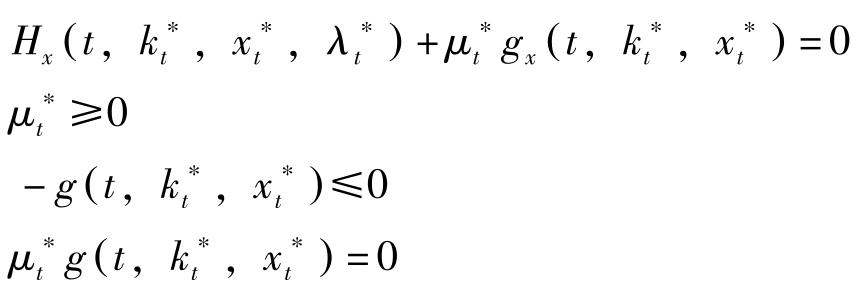
(2)Hamilton动力学:
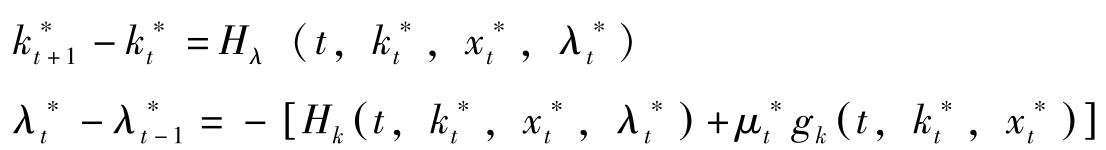
(3)横截性条件(Transversality Condition):
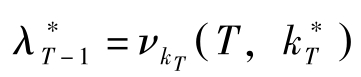
(4)初期条件:
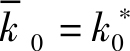
问题(P)的最优解的必要条件(1)~(4)称为最大值原理。
需要说明的是,拉格朗日乘数
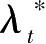 与状态变量
与状态变量
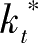 相对应,又称为共状态变量。它表示最优投资
相对应,又称为共状态变量。它表示最优投资
 的边际1单位增加所引起的总效用的增量,因此是投资品的边际价值或投资品的影子价格。
的边际1单位增加所引起的总效用的增量,因此是投资品的边际价值或投资品的影子价格。
混合型(NLP):
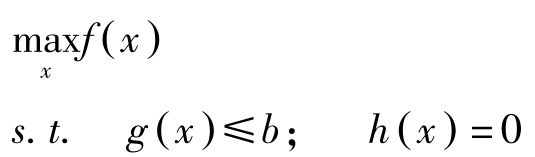
稍作变换即可化为(NLP)的标准问题:
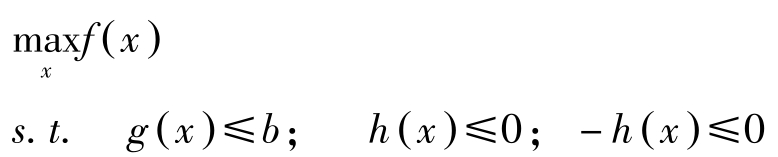
不过, h ( x )与 -h ( x )一般不能同时为凸函数,除非 h ( x )是线性的。因此第1章中约束函数为凸时库恩塔克条件的充分性定理(第1章定理10)以及约束函数为凸且满足Slater条件时的库恩塔克条件的必要性定理(第1章定理9)若要成立,要求 h ( x )必须是线性函数。
与之相对,满足正则性时的库恩塔克条件的必要性定理(第1章定理8)与满足鞍点条件的解为最优解的充分性定理(第1章定理13)依然成立。
记
I
(
x
)={
i|g
i
(
x
)=
b
i
},若
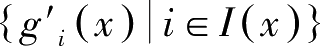 与
与
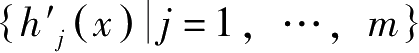 的要素向量线性无关,则称
g
,
h
在
x
满足混合型(NLP)的正则条件。
的要素向量线性无关,则称
g
,
h
在
x
满足混合型(NLP)的正则条件。
记 L + ( x , λ , μ , φ )= f ( x )+ λ [ b-g ( x )]+ μ [0 -h ( x )]+ φ {0-[ -h ( x )]},则混合型(NLP)的库恩塔克条件可表示为:
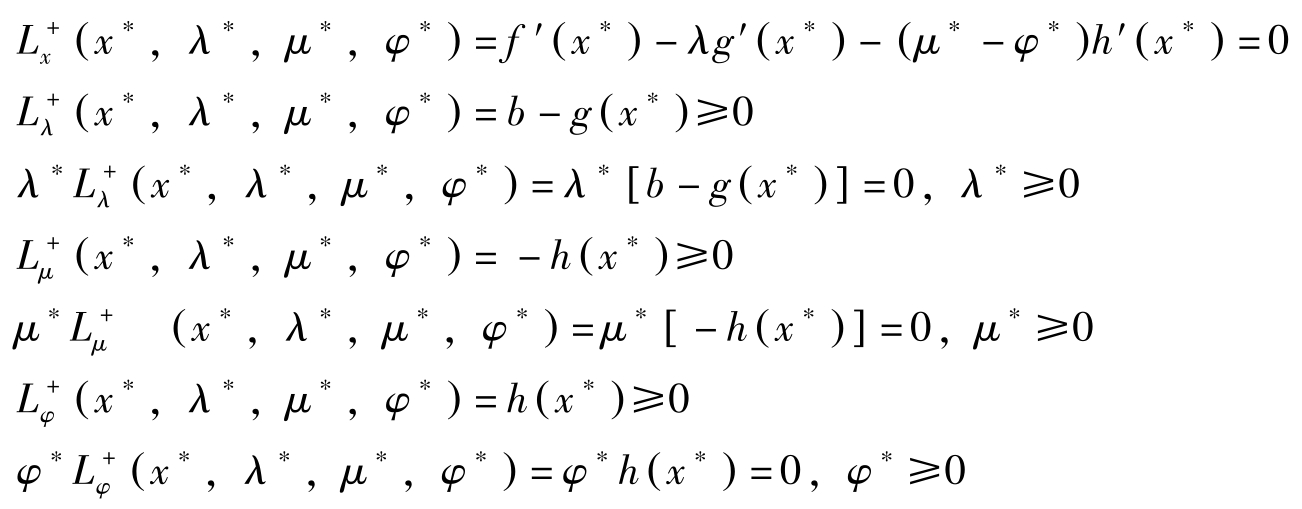
若记 L ( x , λ , ξ )= f ( x )+ λ [ b-g ( x )]+ ξh ( x ),则上述条件与下述条件等价:
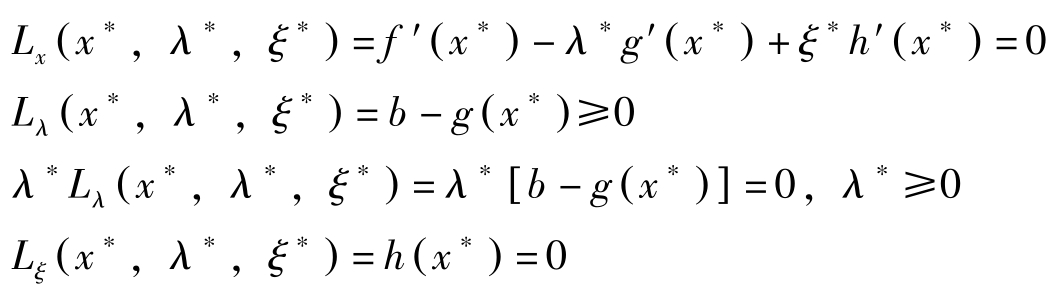
定理3: 对于 x ∗ ,若存在 λ ∗ 与 ξ ∗ 满足库恩塔克条件,并且(i) f ( x ), -g ( x ), h ( x )连续可微、凹;(ii) ξ ∗ ≥0,则 x ∗ 为混合型(NLP)的最优解。
证明: 考虑满足(NLP)约束条件 g ( x )≤ b , h ( x )=0的 x ,由 f ( x )的凹性知
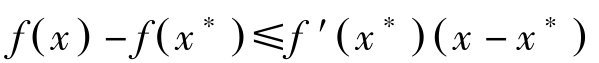
因此
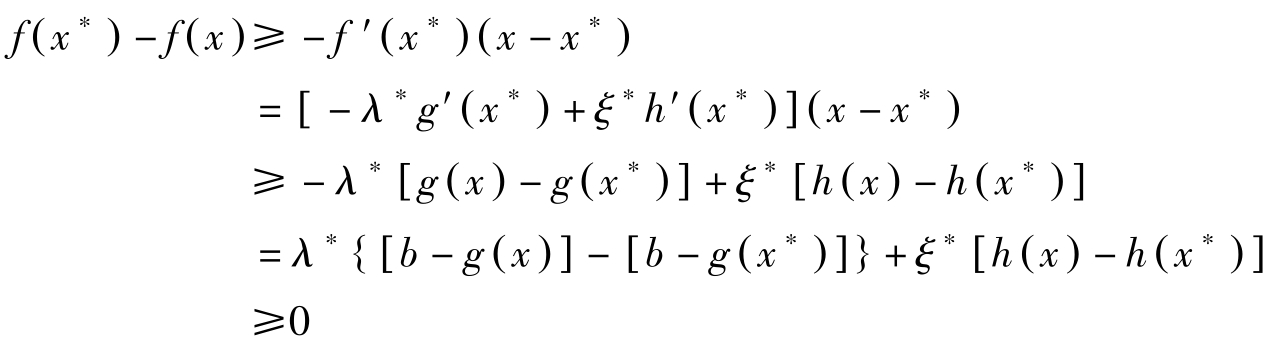
上式第二行取等号是由于库恩塔克条件的第一式成立;第三行取大于等于号是由于 -g ( x ), h ( x )的凹性假定;最后一行取大于等于号是由于 g ( x )≤ b , h ( x )=0, h ( x ∗ )=0以及 λ ∗ [ b-g ( x ∗ )]=0。
该定理中 f 若严格凹,则最优解是唯一的。
定理4: 对于 x ∗ ,若存在 λ ∗ ≥0 与 ξ ∗ ,使对任意的 x ∈ R n , λ ≥0, λ ∈ R m 以及 ξ ∈ R l 都有:
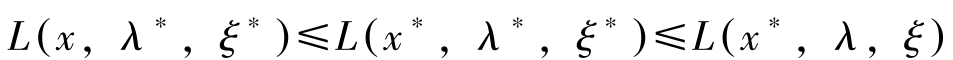
成立,则 x ∗ 为混合型(NLP)的最优解。
证明: 我们首先证明 x ∗ 满足约束条件,再证明对满足约束条件的任意 x 都有 f ( x )≤ f ( x ∗ )即可。
第二个不等式意即
f ( x ∗ )+ λ ∗ [ b-g ( x ∗ )]+ ξ ∗ h ( x ∗ )≤ f ( x ∗ )+ λ [ b-g ( x ∗ )]+ ξh ( x ∗ )
因此对任意的 λ ≥0以及 ξ 均有:
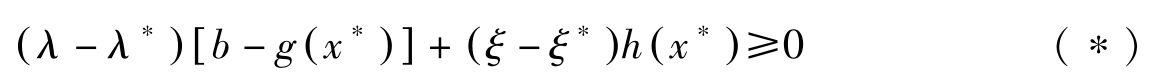
特别地,让 λ j = λ ∗ j +1, j = i ; λ j = λ ∗ j , j ≠ i ; ξ = ξ ∗ ,则 b i ≥ g i ( x ∗ )。对每一个 i 都如是操作,我们有
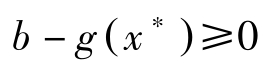
于是 λ ∗ [ b-g ( x ∗ )]≥0。
(∗)式中若令 λ =0, ξ = ξ ∗ ,则有 λ ∗ [ b-g ( x ∗ )]≤0,于是
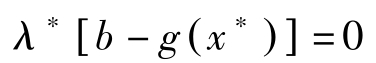
下面让
λ
=
λ
∗
;
ξ
j
=
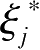 +
ε
,
j
=
i
;
ξ
j
=
+
ε
,
j
=
i
;
ξ
j
=
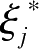 ,
j
≠
i
,于是由(∗)式,
εh
i
(
x
∗
)≥0。
ε
可正可负,因此
h
i
(
x
∗
)=0,这对所有的
i
均成立,于是
,
j
≠
i
,于是由(∗)式,
εh
i
(
x
∗
)≥0。
ε
可正可负,因此
h
i
(
x
∗
)=0,这对所有的
i
均成立,于是
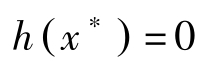
这就是说 x ∗ 满足(NLP)的约束条件。
对于满足 g ( x )≤ b , h ( x )=0的任意 x ,由于 x 满足鞍点条件的第一个不等式,所以
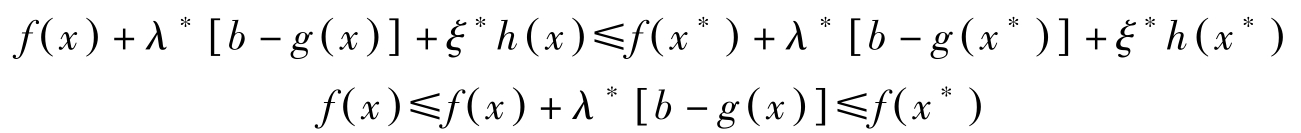
第二行成立是因为 λ ∗ ≥0, g ( x )≤ b , h ( x )=0, h ( x ∗ )=0,以及 λ ∗ [ b-g ( x ∗ )]=0。
沿用2.3.1节的记号。显然有:
(1)若 g ( t , k t , x t )关于 k t , x t 连续可微、凹,则 -G ( X )关于 X 连续可微、凹;
(2)若 f ( t , k t , x t )关于 k t , x t 连续可微、凹, f ( t , k t , x t )+ k t -k t +1 关于 k t +1 , k t , x t 连续可微、凹,因此 H ( X )关于 X 连续可微、凹;
(3)若 u ( t , k t , x t )关于 k t , x t 连续可微、凹,而且 ν ( T , k T )关于 k T 连续可微、凹,则 F ( X )关于 X 连续可微、凹。
注意到以上三点,由定理3我们得:
定理5(最大值原理的充分性):
对于问题(P)中的{
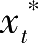 :
t
=0,1,…,
T
-1}与{
:
t
=0,1,…,
T
-1}与{
 :
t
=0,1,…,
T
},若存在{
:
t
=0,1,…,
T
},若存在{
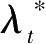 :
t
=-1,…,
T
-1}与{
:
t
=-1,…,
T
-1}与{
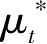 :
t
=0,1,…,
T
-1},满足:
:
t
=0,1,…,
T
-1},满足:
①定理2中的四个条件;②{ λ ∗ t ≥0: t =-1,…, T -1};③ g ( t , k t , x t )、 f ( t , k t , x t )和 μ ( t , k t , x t )关于 k t , x t 、 ν ( T , k T )关于 k T 连续可微、凹。
则{
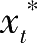 :
t
=0,1,…,
T
-1}与{
:
t
=0,1,…,
T
-1}与{
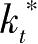 :
t
=0,1,…,
T
}为问题(P)的最优解。
:
t
=0,1,…,
T
}为问题(P)的最优解。
定理 6( 鞍点条件的充分性 ):若问题(P)的拉格朗日函数
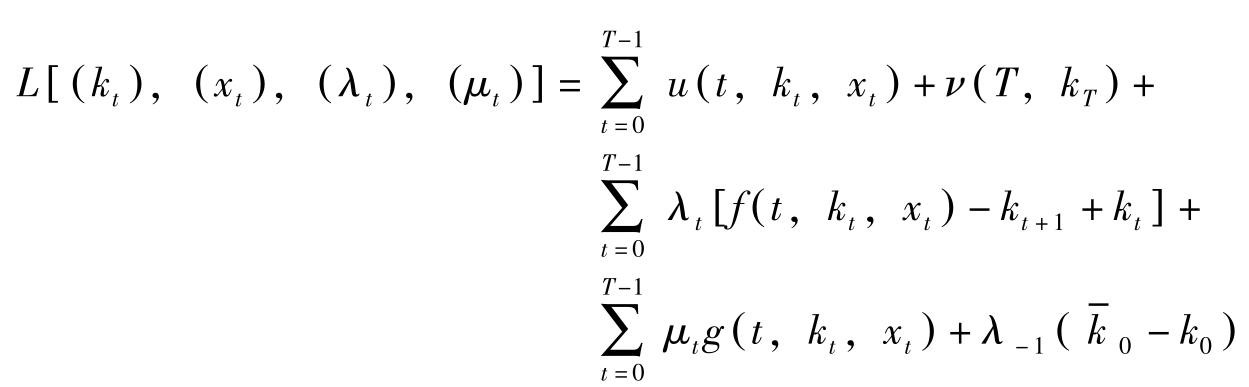
对任意的[(
k
t
),(
x
t
),(
λ
t
),(
μ
t
)],
λ
t
≥0,满足
 那么
那么
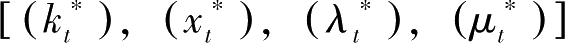 ,
,
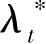 ≥0为问题(P)的最优解。
≥0为问题(P)的最优解。
动态规划方法注重历史的时间推移,在求解问题(P)时,一期一期地依次去求解。在 T 有限时,常运用以下的后向归纳法(Backward Induction)求解。
先看 T 期。在 T 期, k T 已决定,终期效用为 V ( T , k T )。
再看 T -1期。 k T -1 已经决定,选择 x T -1 使今后( T -1期与 T 期)效用最大。即求解下述问题
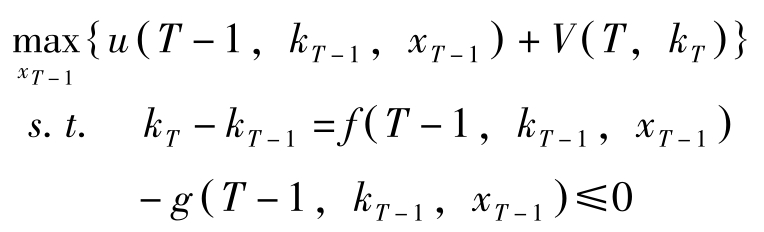
该问题的解假定为
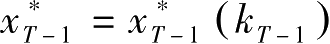 ,目标函数最优值记作
V
(
T
-1,
k
T
-1
),则:
,目标函数最优值记作
V
(
T
-1,
k
T
-1
),则:
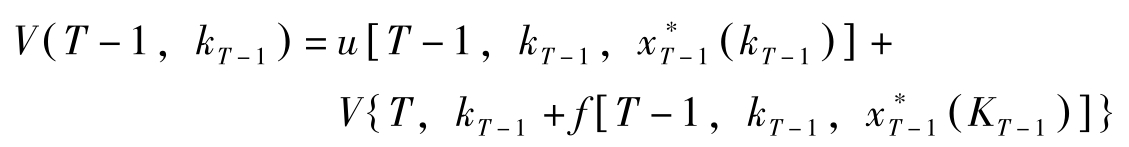
现在看 T -2期。 k T -2 给定,选择 x T -2 使今后效用最大化。即求解下述问题:
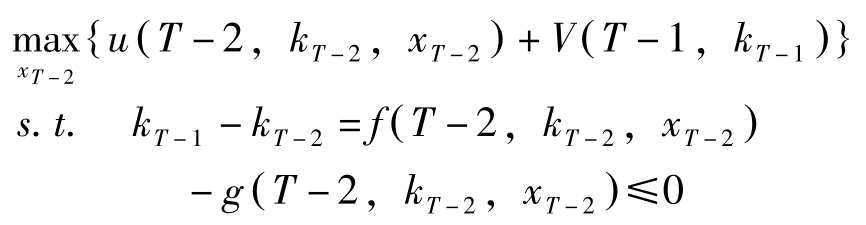
假定该问题的解为
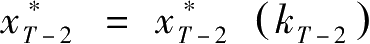 ,目标函数最优值记作
V
(
T
-2,
k
T
-2
),则:
,目标函数最优值记作
V
(
T
-2,
k
T
-2
),则:
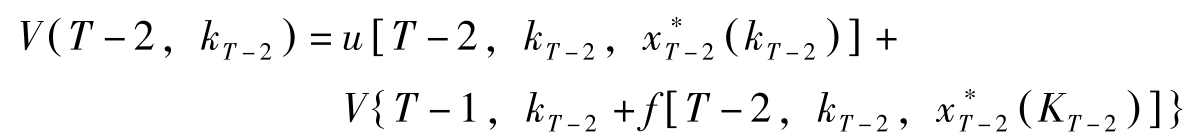
同样的操作持续下去,一般地,在 t 期求解
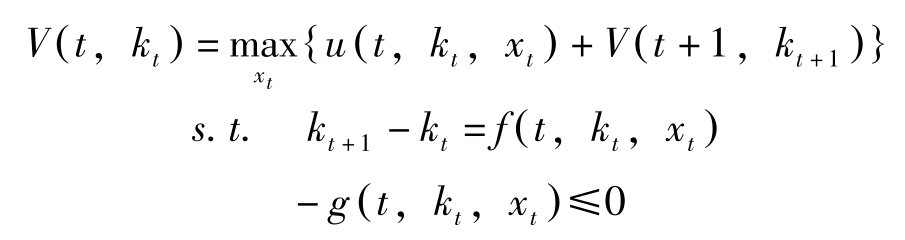
上式也称为“Bellman方程式”。
V ( t , k t )称为“状态评价函数”, x ∗ t ( k t )称为“政策函数”。
就这样每一期的政策函数依次被决定。计划期全体的政策函数与状态运动方程的关系可表示如下:
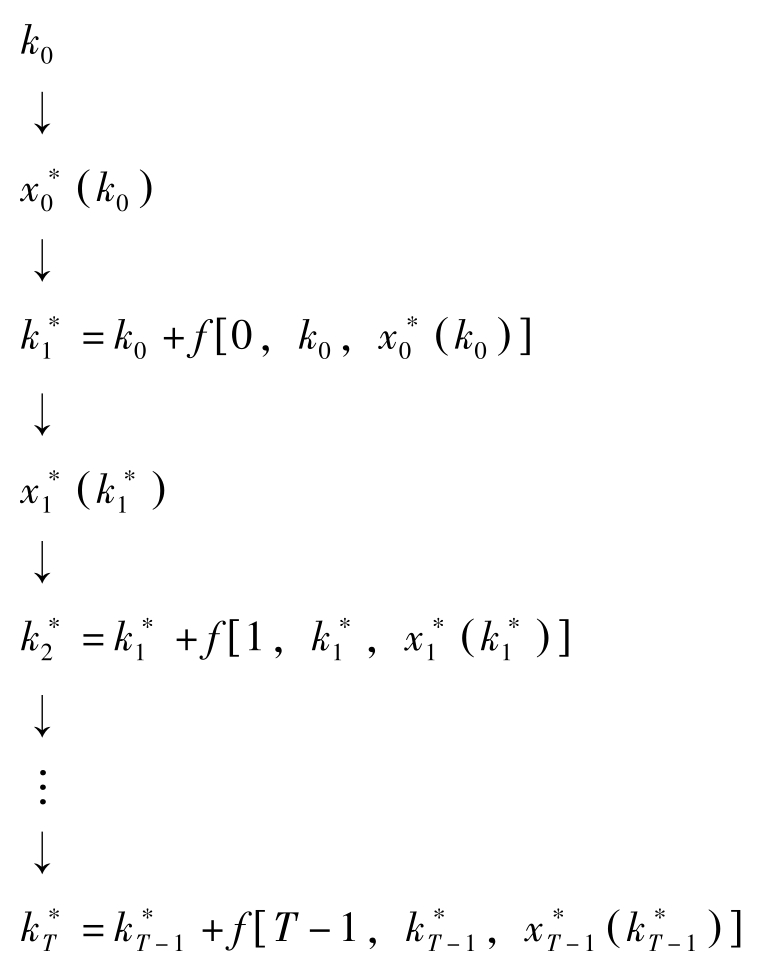
这样,动态规划的特征就是将整个计划期的最优化变为每一期的最优化,利用后向归纳法直接导出每一期的政策函数。
下面我们将从动态规划方法推导出最大值原理。为使推导简单化,假定:
(1)不等式约束 -g ( t , k t , x t )≤0不起作用(not binding)。
(2)动态规划问题的政策函数 x ∗ t ( k t )关于 k t 连续可微。
由定义,
V ( t , k t )= u [ t , k t , x ∗ t ( k t )]+ V { t +1, k t + f ( t , k t , x ∗ t ( k t )]}; t =0,…, T -1
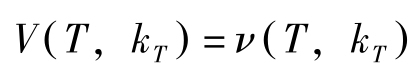
成立。假定 u , f , v 连续可微,则 V ( t , k t ), t =0,…, T -1也连续可微。
假定动态问题(P)的动态规划解为
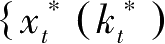 }与
}与
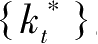 。因而是
。因而是
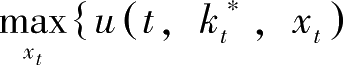 +
V
[
t
+1,
+
V
[
t
+1,
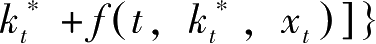 的最优解,于是满足
的最优解,于是满足
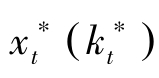
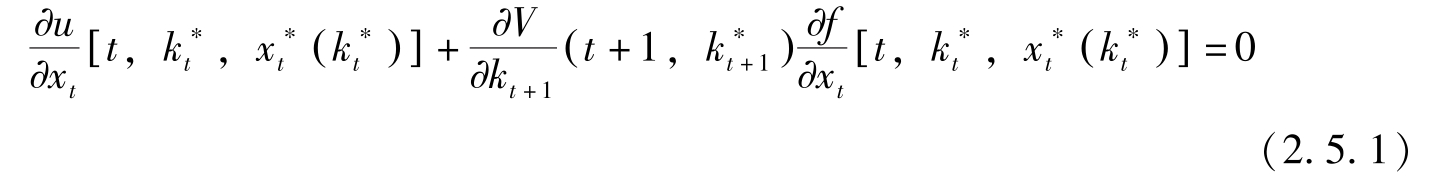
定义
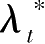 与
H
(
t
,
k
t
,
x
t
,
λ
t
)如下:
与
H
(
t
,
k
t
,
x
t
,
λ
t
)如下:
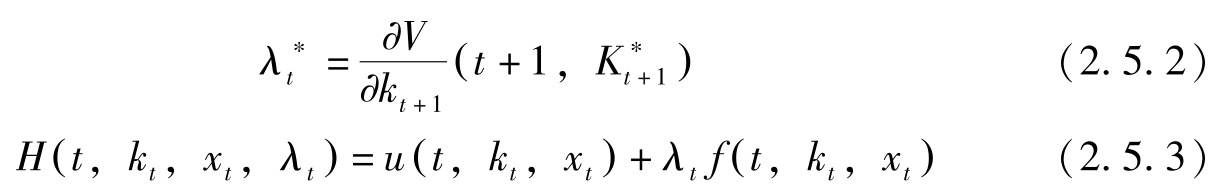
则(2.5.1)可表示为:
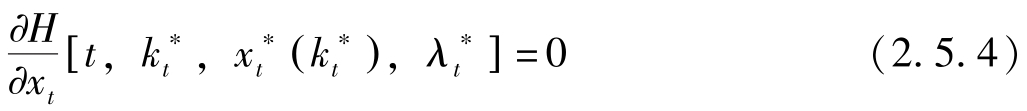
注意到
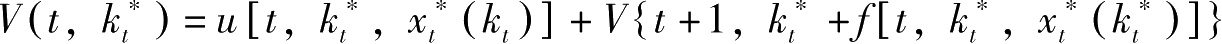 ,两边对
k
t
微分并利用式(2.5.1),有:
,两边对
k
t
微分并利用式(2.5.1),有:
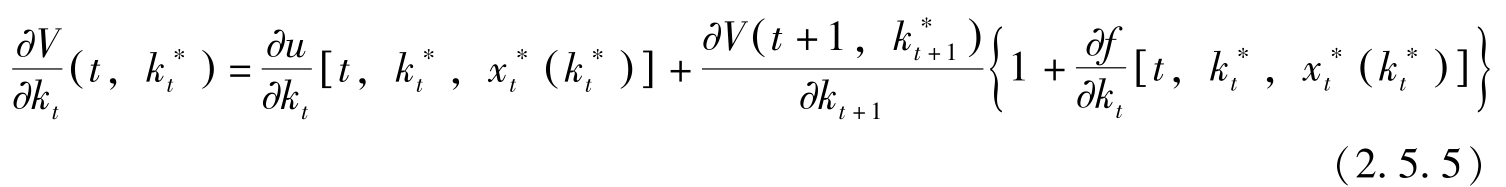
由式(2.5.2)与(2.5.3),上式可写作
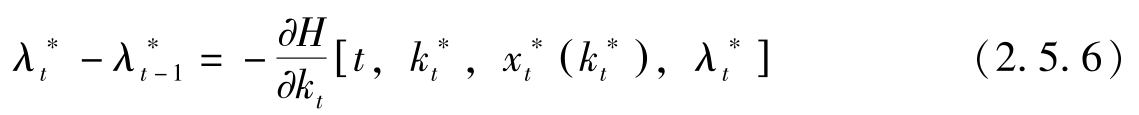
另一方面,由(2.5.3)与状态方程可得:
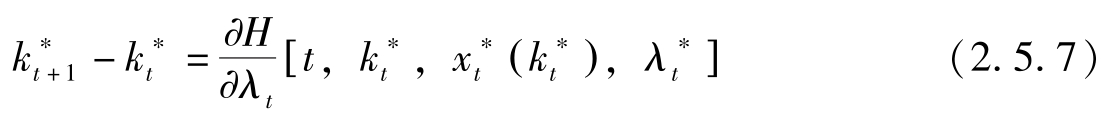
最后由定义
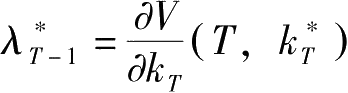 与
V
(
T
,
k
T
)=
ν
(
T
,
k
T
)有
与
V
(
T
,
k
T
)=
ν
(
T
,
k
T
)有

期初条件为:

就这样,我们从动态规划出发推导出了最大值原理。式(2.5.4)、(2.5.6)、(2.5.7)、(2.5.8)与(2.5.9)就是满足假定(1)与(2)的动态问题(P)的最大值原理。
这里需要强调的是定义(2.5.2)式的含义。(2.5.2)式错开一期有
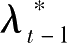 =
=
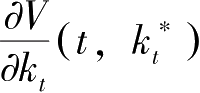 。
。
该式左边为 t -1期投资品 k t -k t -1 的影子价格, V ( t , k t )表示 t 期资本的总价值,右边表示 t 期资本的边际价值,也即 t 期资本的影子价格。该式表明 t -1期投资品价格必须等于 t 期资本的价格。
定义 x t = k t -k t -1 ,则(P V )转换成(P V ′)
(P V ′)
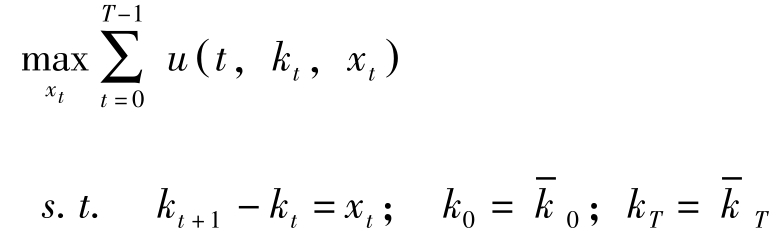
(P V ′)的Hamilton函数为 H ( t , k t , x t , λ t )= u ( t , k t , x t )+ λ t x t ,最大值原理为:
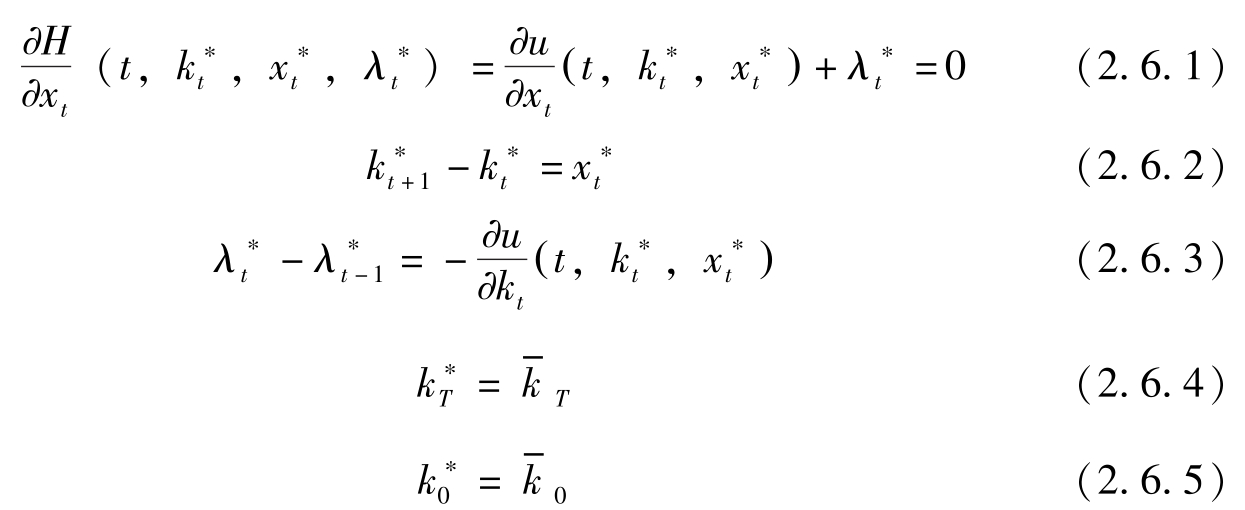
将(2.6.1)式与(2.5.2)式代入(2.6.3)式有
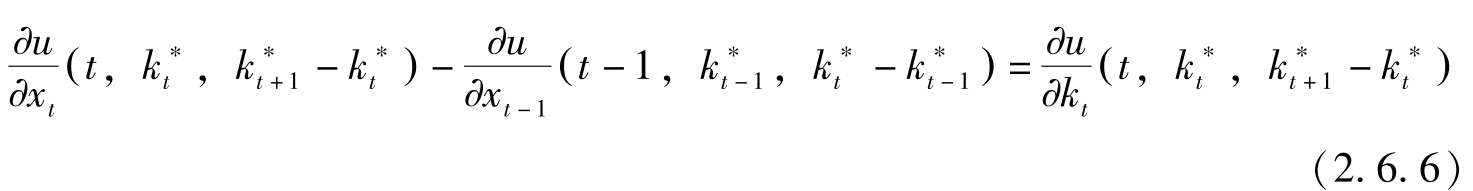
该式即为Euler差分方程式。因此从最大值原理出发导出了变分法的结果。值得特别注意的是(2.6.1)式:
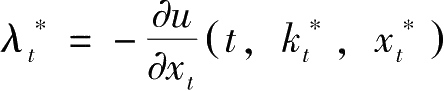 右边是由
t
期的最优投资引起的当期效用的边际减小值的反函数,它必须等于左边的投资的价格。
右边是由
t
期的最优投资引起的当期效用的边际减小值的反函数,它必须等于左边的投资的价格。